GNSS大气加权平均温度经验模型精化方法的建立和分析

杨 飞，郭际明，陈 明，章 迪

1. 中国矿业大学(北京)地球科学与测绘工程学院，北京 100083； 2. 武汉大学测绘学院，湖北 武汉 430079； 3. 国家基础地理信息中心, 北京 100830

随着GPS气象学概念的提出[1]，学者们一直致力于开发和改进基于GNSS反演大气可降水量的方法，这使得GNSS成为一种高效、可靠的水汽遥感技术，它具有全天时、全天候、连续运行、低成本、高分辨率及高精度等优点[2-5]。在获取大气可降水量PWV时，需要将天顶湿延迟乘以转换因子，它是加权平均温度Tm的一个函数[6]。因此，准确计算Tm是GNSS获取高精度大气可降水量的关键。Tm是测站上空的温度和湿度廓线沿着天顶方向的数值积分，可以通过无线电探空、大气再分析资料精确计算。然而，全球探空测站分布稀疏，空间分辨率难以满足GNSS气象学需求；大气再分析资料的时间分辨率较低且通常每月更新一次；难以满足实时/近实时Tm计算的要求[7-8]。

文献[1]收集了位于27°N～65°N之间的13个美国探空测站数据并对8718个探空剖面进行分析，发现Tm与地表温度Ts存在很好的线性关系，建立了Bevis公式，成为当前使用最为广泛的Tm线性回归模型。虽然Ts的地理和季节变化可以反映出Tm的地理和季节变化，但基于北美探空数据建立的Bevis公式往往存在区域性的精度差异。因此，学者们进行了大量研究来建立Tm和Ts的区域线性回归模型[9-14]。此外，只须测站位置和时间信息的经验模型逐渐成为Tm计算的主要方法。文献[15]利用2005—2009年全球135个探空测站数据，基于全球气压和温度(GPT)模型构建了GWMT模型，并通过优化建模方法和改善建模源数据提出了一系列改善模型，如GTm-Ⅱ、GTm-Ⅲ、GWMT-Ⅳ、GTM-X及GWMT-D[16-20]。文献[21]考虑了纬度和海拔变化，利用滑动窗口算法建立了GGTm模型。文献[22]提出了考虑线性趋势、年变化、半年变化及空间变化的GTrop模型。此外，经验对流层模型GPT3和UNB3m同样可以提供Tm估值[23-24]。由于开源、易操作、网格分辨率及精度高且可以提供其他对流层参数，GPT3模型成为当前使用最为广泛的Tm经验模型。

研究表明Tm经验模型精度往往低于Tm回归模型[25-27]。为了提高经验模型估计Tm的精度，本文提出一种Tm经验模型的精化方法，它引入地面气温数据并通过最小二乘方法快速获取精化系数，达到对Tm的误差补偿作用。相较基于机器学习等精化方法，本文方法计算公式简便，可以快速推广至任意Tm经验模型，达到模型精化的目的，对改善GNSS水汽反演精度有重要的现实意义。

1 Tm计算原理及模型建立

加权平均温度Tm是由测站上空的水汽压和气温在天顶方向的数值积分计算得到的，文献[28—29]给出了Tm的定义及精确计算Tm的方法

(1)

式中，T是大气温度，单位为K；e是水汽压，单位为hPa；z为测站上空的垂直高度，单位为m。在常规的探空数据资料中，上述气象参数及高程信息均不是连续值，往往以高度分层的形式存储。因此，式(1)的离散化形式常用于Tm的精确计算

(2)

式中，下标i代表第i层的气象参数信息。

Bevis模型是基于美国13个无线电探空站2 a的观测资料，共8712条探空廓线建立起来的Tm与Ts线性回归模型

Tm=70.2+0.72·Ts

(3)

基于10 a的ECMWF再分析资料的37个气压层月平均数据，文献[23]提出了GPT3模型。作为GPT系列模型的最新版本，GPT3模型可以提供全球范围内1°×1°格网点上加权平均温度的平均值、年周期和半年周期变化。依据测站位置和时间信息，可以利用式(4)快速获取其Tm估值

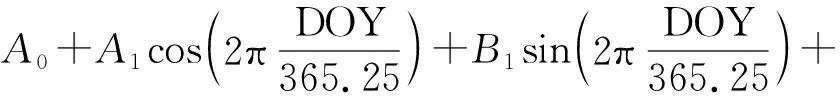
(4)

式中，A0表示模型格网点Tm的平均值；A1和B1表示模型格网点Tm的年振幅；A2和B2表示其半年振幅。

由于GPT3模型的建模源是月平均数据，其模型只包含年和半年周期项，缺乏表示Tm随高程变化的Tm递减率参数，其精度往往受到限制。通过对实测Tm与GPT3估计Tm的差异和实测Ts与GPT3估计Ts的差异进行分析，其线性相关系数达到了0.62，如图1所示(使用第2节试验中的数据)。因此，本文提出一种GPT3模型估计Tm的精化方法，它将地面气温数据引入并利用最小二乘获取精化系数。具体地，该精化模型如式(5)所示

Tm=TmGPT3+M·(Ts-TsGPT3)

(5)

式中，Tm和Ts分别为加权平均温度真值和地表温度真值；TmGPT3和TsGPT3分别表示由GPT3模型估计得到的加权平均温度和地表温度；M表示实测地表温度和模型估计地表温度差异的权值，即精化模型的精化系数，可以通过最小二乘拟合得到。

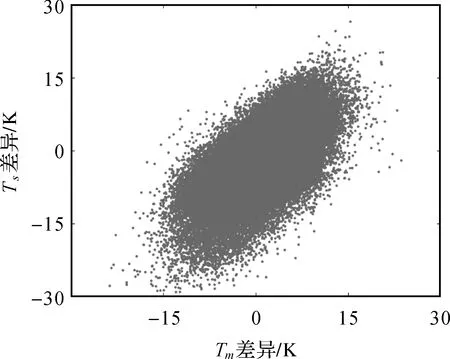
图1 Tm差异与Ts差异示意图(实测值与GPT3估值)Fig.1 The diagram of Tm differences and Ts differences (measured values and GPT3 estimates)

2 试验描述

本文选择2011—2015年我国与邻近区域的探空站点资料，以及对应的地面气象资料进行GPT3模型区域精化。探空数据分辨率为12 h，即每天固定在UTC 0:00和UTC 12:00。探空剖面包括了不同高度的气压、温度等气象信息。为了计算准确的Tm，需对探空剖面信息进行严格的质量控制，只有满足以下条件的剖面数据才可以用式(2)计算Tm[26]：①探空数据中最后一个有效记录的高度不低于10 km；②探空数据中有效的观测值数量不少于20个；③两个连续高度层之间的高差应不超过1 km；④任何两个连续高度层的气压差值不大于200 hPa。

经过质量控制，本文选取我国及邻近区域180个探空测站，其范围为0°N～65°N，60°E～145°E，如图2所示。图2(a)表示用于模型精化的130个探空测站的分布情况。通过GPT3模型，利用双线性内插算法并考虑测站与模型格网点高程差异，可以获取这些测站的Tm和Ts估值[23]。联合探空测站数据获取的精确加权平均温度和地表温度，便可利用式(5)拟合得到本文中模型精化系数M=0.47，构建基于GPT3的精化模型。图2(b)表示用于模型精度检验的50个探空测站分布。

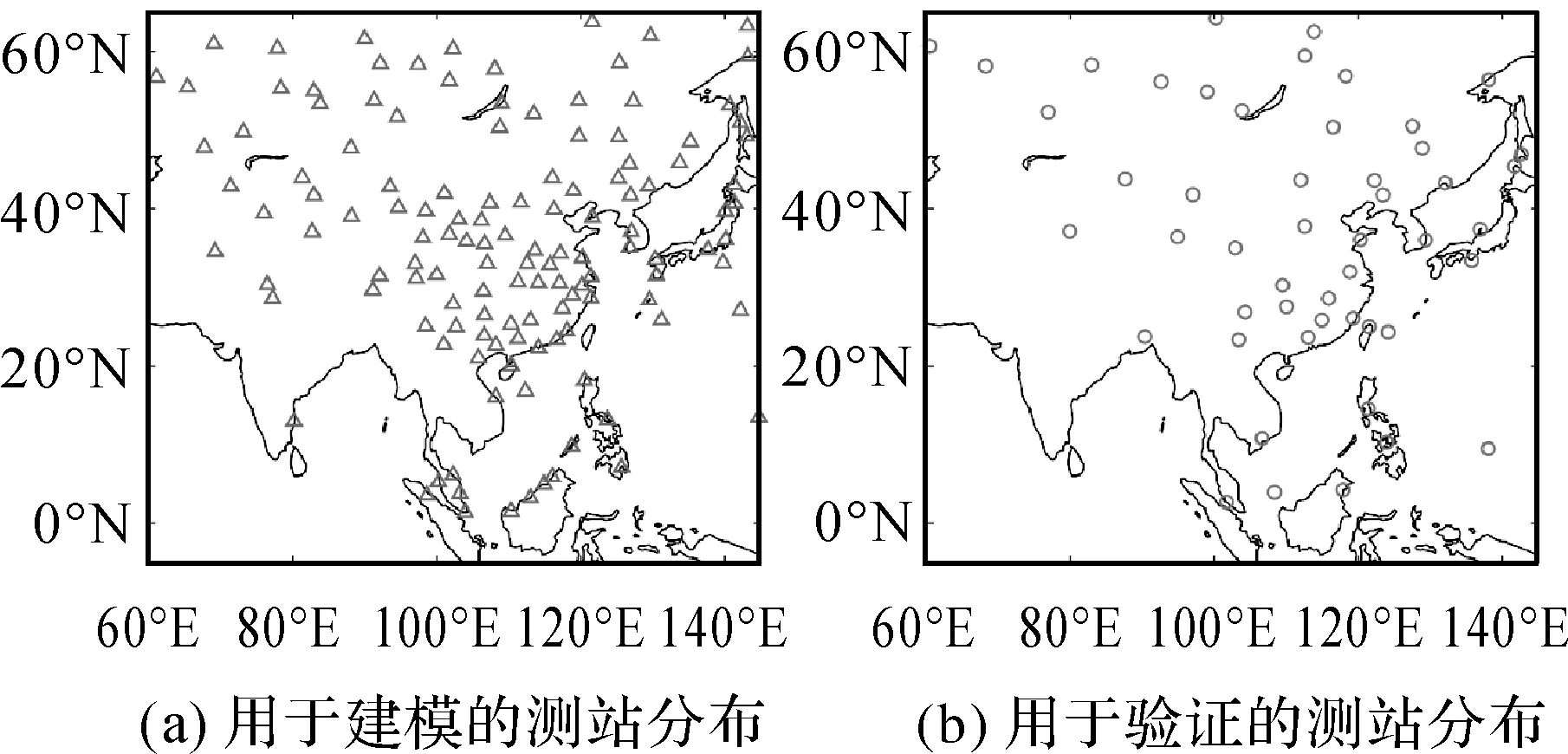
图2 研究区域及测站分布Fig.2 The map of the research area and the distribution of the sites

为了验证所提精化模型的优势，本文还利用上述130个探空测站的地面气温和加权平均温度信息，基于Beivs模型的思路，构建了上述研究区域的Tm-Ts线性模型。区域线性模型表达为Tm=53.45+0.78·Ts。因此，本文比较了4种模型在我国及邻近区域估计Tm的精度。它们分别为Bevis模型、区域线性模型、GPT3模型和基于GPT3的精化模型。本文选取3个统计量，即均方根误差(RMSE)、平均绝对误差(MAE)及相关系数(R)作为标准来比较和评价4种模型估计Tm的精度。

3 精度比较与分析

利用上述4种模型，分别计算50个验证测站2011—2015年不同时刻的Tm，共141 110个数据。将探空剖面信息计算的相应时刻Tm作为参考值，绘制了散点图，如图3所示。图中虚线表示1∶1的直线，直线表示模型Tm估值与Tm真值的线性拟合直线。可以发现，基于GPT3的精化模型表现优于其他3种模型，其点分布在拟合线附近的密度高于其他模型，且其斜率达到了0.93。相较于Bevis模型，区域线性模型的点位分布密度没有明显差别，但其拟合斜率得到有效改善，说明构建局部区域Tm-Ts线性模型可以提高Tm估计精度。注意到GPT3模型估计的Tm有明显的界限(图中方框位置)，即无论真实Tm值变得多小或多大，GPT3估计的Tm值总为243 K或290 K左右。而基于GPT3的精化模型较好地解决了这一问题，使其可以准确估计任何范围的Tm值。

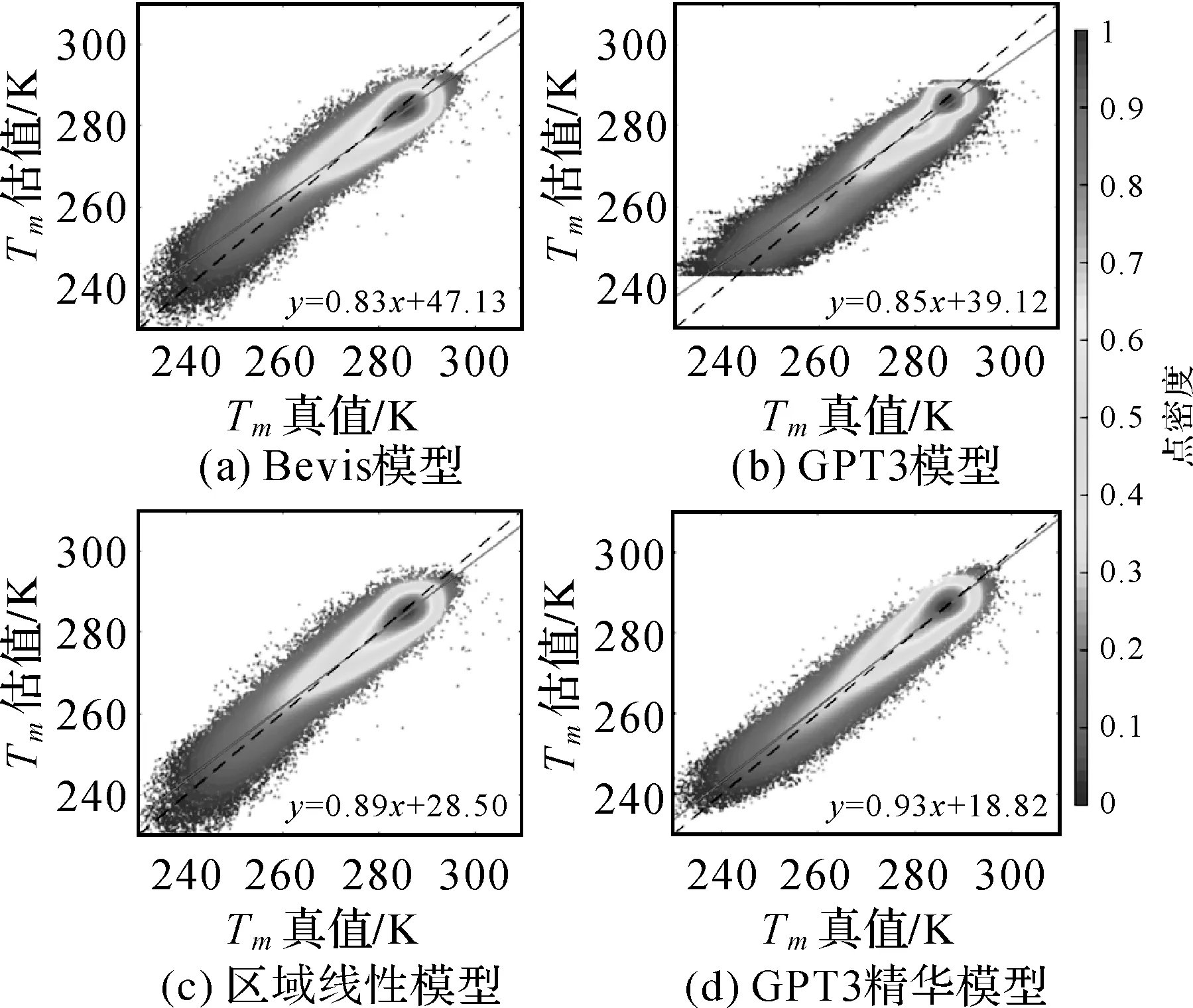
图3 4种模型Tm估计值与Tm真值的散点图Fig.3 The scatter plots of the estimated Tm against the true Tm with four models

此外，利用4种模型估计Tm的残差计算了它们各自的MAE和RMSE，不同模型估计Tm与Tm真值的相关系数R也被统计，并列于表1。GPT3模型表现最差，其MAE、RMSE和R分别为3.43 K、4.46 K和0.94。基于GPT3的精化模型不仅有效改善了GPT3模型的精度，也优于基于Tm-Ts线性关系的区域模型的精度。相较于其他3种模型，基于GPT3的精化模型对MAE和RMSE的改善量分别达到了0.53、0.68、0.38 K和0.68、0.94、0.55 K。

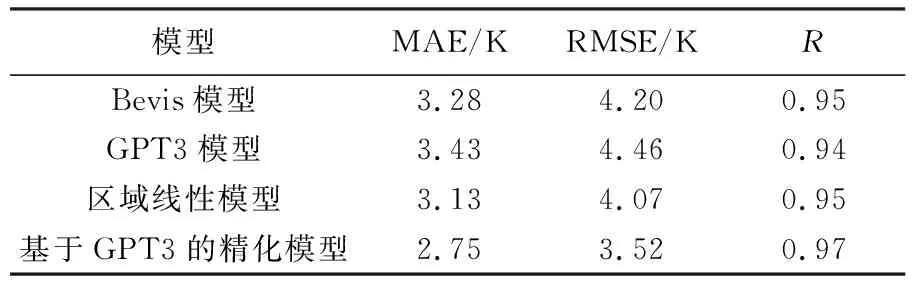
表1 4种模型估计Tm残差的统计

为了分析4种模型在不同区域估计Tm的表现，计算并统计了每种模型在每1个验证测站估计Tm与Tm真值的残差。图4展示了4种模型估计Tm在各个测站RMSE的空间分布。可以看到，4种模型估计Tm的精度都会受到纬度的影响，即随着纬度的增大精度变差。Bevis模型、GPT3模型和区域线性模型在中高纬度地区估计Tm的精度都较差，甚至出现大量RMSE>6 K的测站。受限于GPT3模型本身在中高纬度较差的表现及Tm在中高纬度区域的变化和波动较大，基于GPT3的精化模型估计Tm的精度也存在纬度上的差异。但是，依然可以看到基于GPT3的精化模型显著改善了其在中高纬度区域估计Tm的精度，其对Tm精度的改善率与其他区域是一致的。另外，基于GPT3的精化模型在其他纬度区域测站的表现同样优于其他3种模型。

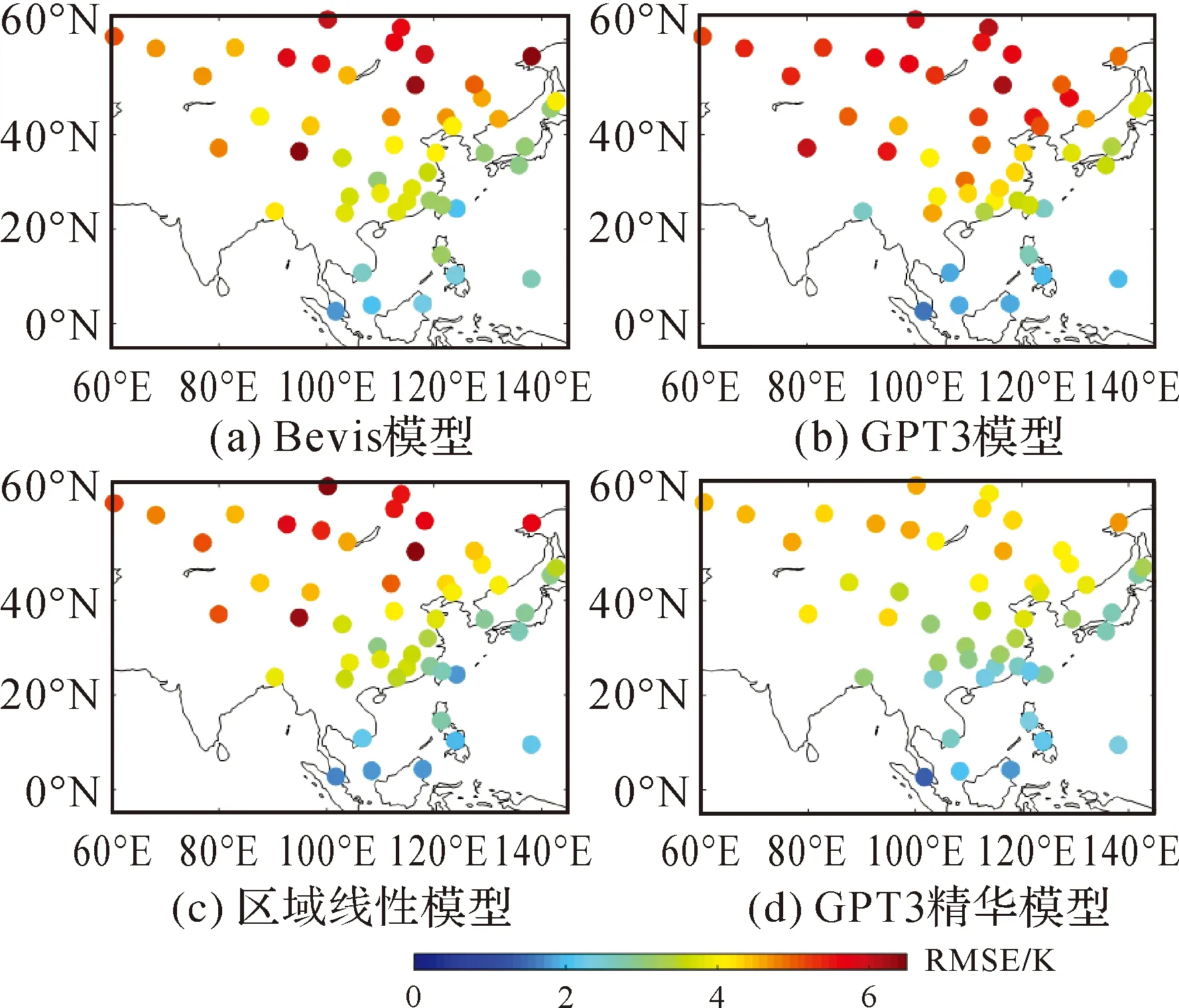
图4 4种模型估计Tm的RMSE在不同测站空间分布Fig.4 The spatial distribution of RMSE at each site for the four models

表2统计了4种模型在不同测站估计Tm的MAE和RMSE，包括最大值、最小值和平均值。可以看到，MAE和RMSE的最大数值都出现在Bevis模型，说明Bevis模型难以服务于全球或大区域的Tm估计，在某些测站会出现较大误差。注意到GPT3模型RMSE和MAE的最大值和最小值都小于Bevis模型和区域线性模型的相应统计量。这表明该测站的Tm变化与建立的整个区域Tm-Ts线性关系不符，需要更加具体、范围更小的区域线性模型。而基于GPT3的精化模型的所有统计量都是4种模型中最小的，其中MAE和RMSE的平均值分别为2.71 K和3.44 K，改善量分别达到了17.1%、20.1%、13.1%和16.7%、20.7%、13.4%。

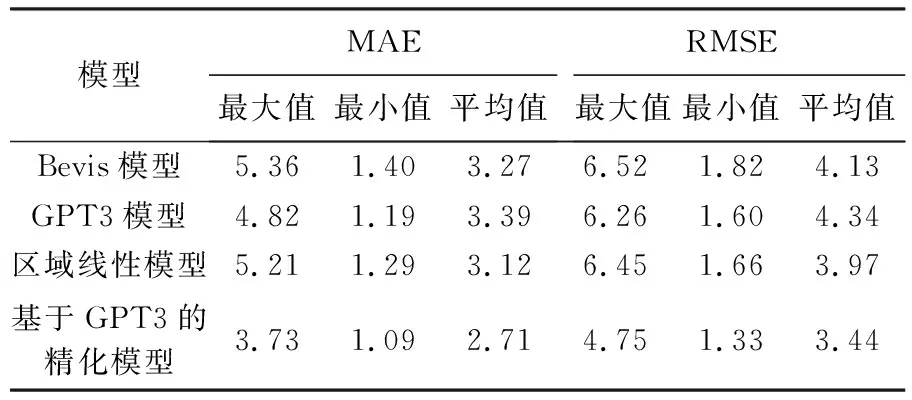
表2 4种模型在不同测站的精度统计

为了分析4种模型估计不同时刻Tm的精度情况，本文计算并统计了2011—2015年不同模型在每天的RMSE，其时间序列如图5所示。可以看到，4种模型的RMSE表现出明显的周期性，在冬季总体较大，夏季较小。这是由于Tm本身季节幅度的差异造成，冬季Tm幅度大，往往会使得Tm建模结果变差，导致较大的RMSE。基于GPT3的精化模型得到的RMSE时间序列明显优于其他3种模型，几乎每天都可获得最小的RMSE。进一步，表3详细给出了不同模型在4个季节估计Tm的RMSE。可以看到，基于GPT3的精化模型在不同季节的RMSE分别为3.83、3.01、3.69、4.06 K，相较于GPT3模型，不同季节的改善量分别达到1.07、0.87、0.85、0.85 K。

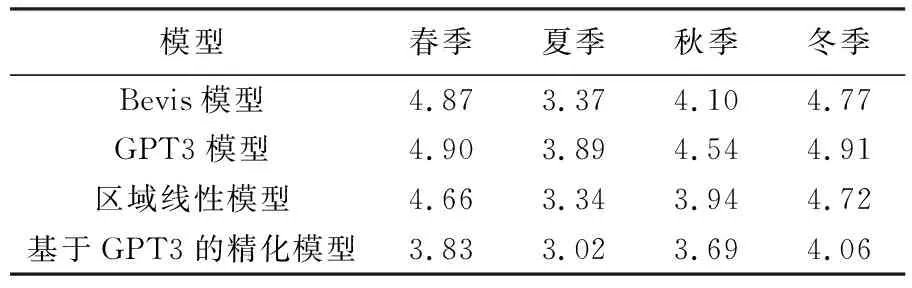
表3 4种模型在不同季节估计Tm的RMSE

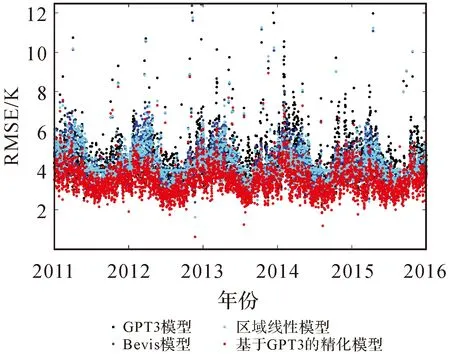
图5 4种模型在不同时刻的RMSE序列Fig.5 The RMSE of the four models at different days

为了更好地理解精化模型对于GPT3模型精度改善的原因，图6绘制了GPT3模型和基于GPT3的精化模型在不同测站估计Tm的时间序列，且将Tm真值的时间序列作为参考。图6选取了6个不同区域的测站，这些测站经质量控制后Tm观测值的数量较多。可以看到，在每1个测站，GPT3模型估计的Tm都是一条平滑的周期曲线，只能表现出Tm的季节性变化。而基于GPT3的精化模型在这些测站可以模拟出更复杂的Tm变化，表现出Tm在短时间内的波动和突变，与探空得到的Tm真值具有更好的一致性。

4 结 论

本文提出一种Tm经验模型精化方法，引入地面气温数据并通过最小二乘方法快速获取精化系数，达到对Tm的误差补偿作用。其计算公式简便，可以快速推广至任意Tm经验模型。

基于我国及周边地区180个探空测站，本文开展了区域GPT3模型精化试验和分析。验证结果表明，所提出的基于GPT3的精化模型估计Tm的MAE、RMSE和R分别为2.75 K、3.52 K、0.97，有效改善了GPT3模型的精度，改善量分别为19.9%、21.1%、3.2%；且比基于Tm-Ts关系的Bevis模型和区域线性模型精度要高。此外，空间分布分析表明，基于GPT3的精化模型可以改善传统Tm模型受到纬度的影响，显著提高高纬度区域Tm估计精度；时间序列分析表明基于GPT3的精化模型在不同年积日都可以获得最好的Tm估计，且可以有效解决GPT3模型只能表现Tm季节性变化的缺陷。因此，本文提出的Tm经验模型精化方法可以应用到GPT3模型估计Tm的快速精化中，也可以进一步推广至其他Tm经验模型的精化工作中。

图6 模型估计的Tm和探空Tm在不同测站的时间序列Fig.6 The Tm time series estimated from the two models and radiosonde observations at different sites