基于高斯过程回归的橡胶玻璃化温度的预测研究

陈祝丹，李大字*，刘 军，高 科

（1.北京化工大学 信息科学与技术学院，北京 100029；2.北京化工大学 材料科学与工程学院，北京 100029）

玻璃化温度（Tg）作为聚合物的重要工艺指标，指聚合物高弹态与玻璃态之间的转换温度。溶聚丁苯橡胶（SSBR）[1]在Tg以上表现为具有高弹性的高弹态，在Tg以下表现为具有脆性的玻璃态。由于橡胶的Tg会影响其物理性能、阻尼性能、耐热性能等，其一直是橡胶性质的重要指标。

影响合成橡胶Tg的因素包括聚合物中各组分含量和微观结构等[2-3]。合成橡胶的Tg通常采用差示扫描量热仪、动态热机械分析仪等测试[4-6]，Tg测试值会随测试方法和条件的变化而改变，且无法预测Tg，即测试缺乏扩展性和灵活性；测试过程需进行重复试验，消耗大量的人力和物力，测试结果还会受到设备的影响。不同苯乙烯和丁二烯含量的SSBR的Tg不同，要实现其良好表征，目前测试方法的预测分析能力受到极大地限制。

随着机器学习在材料学科的应用越来越广泛[7-9]，研究学者开始开发新的方法研究高聚物的Tg测试。通过神经网络来建立高聚物的Tg预测模型是一种普遍且备受关注的方法[10]，但神经网络也有很多不足。神经网络需要依赖训练数据，数据的多样性和数量对网络性能具有重大影响。橡胶每次合成和表征都需要研究人员进行设计和反复试验，这限制了训练数据的多样性。

高斯过程回归[11]是基于统计学理论，可以在模型搭建的过程中自适应地得到超参数，并给予预测输出明确的概率解释。因此，与反向传播（BP）神经网络相比，高斯过程回归具有更少的参数和更快的收敛速度，以及对小样本、非线性问题具有难以取代的优势[12]。

本工作以实例数据为样本，利用高斯过程回归模型分析苯乙烯和丁二烯含量对SSBR的Tg的影响，从而预测Tg，以期为实际生产过程中预测和控制橡胶的Tg提供参考。

1 高斯过程回归

高斯过程回归是一种贝叶斯学习框架下的无参数核方法[13-14]。通过直接对函数建模，产生非参数模型。对训练输入数据X＝x1，x2，x3，…，xn，x*及其对应输出数据Y＝y1，y2，y3，…，yn，y*建立的回归方程为

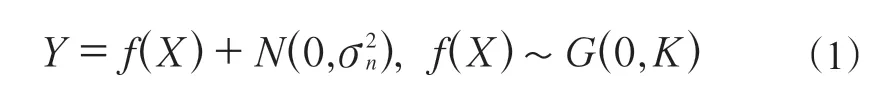
式中：回归函数f（X）不需要指定具体形式，可以认为是在高斯回归过程中采样得到的一个无穷维的点；N（0,n2σ）表示均值为0、方差为n2σ的噪声；G（0，K）是均值为0、协方差为K的高斯回归过程；对于新输入x*和对应输出y*仍有相同的映射关系。

利用协方差函数，即核函数反映高斯回归过程中数据点之间的相互关系，本课题选取径向基（RBF）核函数作为协方差函数：

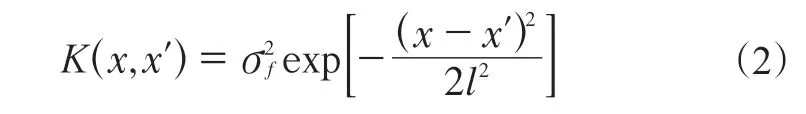
式中，K（x,x′）是x与x′之间的协方差，σf和l为可调节的参数。

要求取一个新输入x*及其对应输出y*依然满足上述高斯分布，利用上述协方差矩阵可以得出式（3）和（4）：

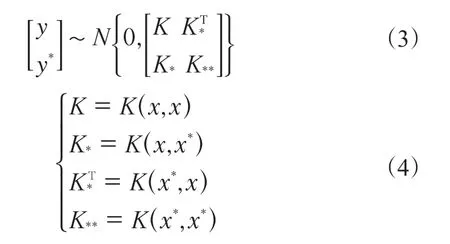
根据贝叶斯回归方法，预测数据y*的条件分布P（y*｜y）服从如下高斯分布：

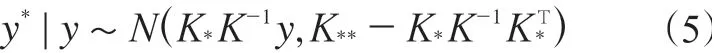
分布的均值可以作为y*的估计值：

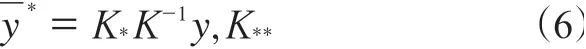
分布的协方差表示预测值的不确定性：

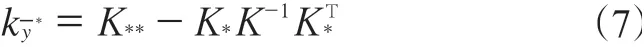
因此，高斯过程回归模型不仅可以模拟任何黑盒模型，还可以计算置信区间，即计算模拟的不确定性。

2 结果与分析

本课题采用数据从文献[15]中获取，在橡胶合成过程中，采用复合结构调节剂调节苯乙烯和丁二烯含量，合成了多种结构的SSBR，研究苯乙烯含量对SSBR的Tg的影响。试样包含12种苯乙烯含量的SSBR，其苯乙烯含量为5%～45%，丁二烯含量为24%～78%。不同苯乙烯和丁二烯含量SSBR的Tg如表1所示。其中，1#—8#试样数据构建高斯过程回归模型，9#—12#试样数据验证模型的有效性。

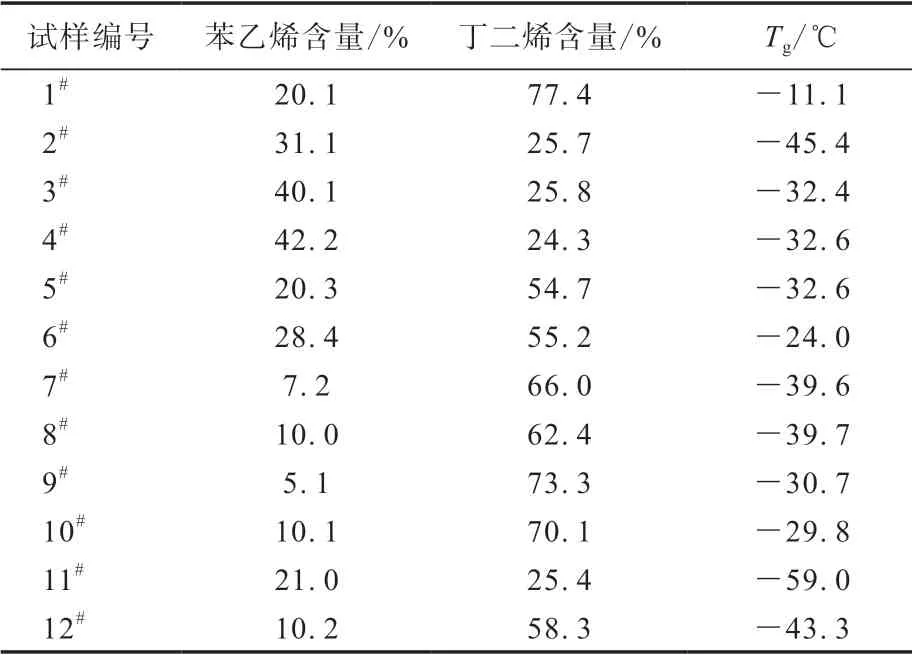
表1 不同苯乙烯和丁二烯含量的SSBR的TgTab.1 Tg of SSBR with different styrene and butadiene contents

利用表1中1#—8#试样数据作为训练数据，参数设置为σf和l，建立高斯过程回归模型。同时，利用相同的训练数据和测试数据，本课题构建BP神经网络模型作为对比试验。为了提高BP神经网络模型的预测能力，对训练数据和测试数据进行了归一化处理。通过多次试验，优化选取了2-8-1网络结构，即网络有3层，输入层包含2个节点、隐含层包括8个节点、输出层包含1个节点，学习率设为0.2。

SSBR的Tg测试数据和训练数据输出结果如表2所示。测试误差采用绝对误差和相对误差来表示，前者反映误差的大小，后者是绝对误差占真值的百分比，可以反映误差的偏离程度。

从表2可以看出，BP神经网络模型Tg预测值的最大绝对误差和最大相对误差分别高达26.47 ℃和44.9%，高斯过程回归模型预测的最大绝对误差和最大相对误差分别为2.37 ℃和5.5%，后者结果更理想。高斯过程回归模型的偏差远小于BP神经网络模型，表明高斯过程回归模型的可靠性和有效性。

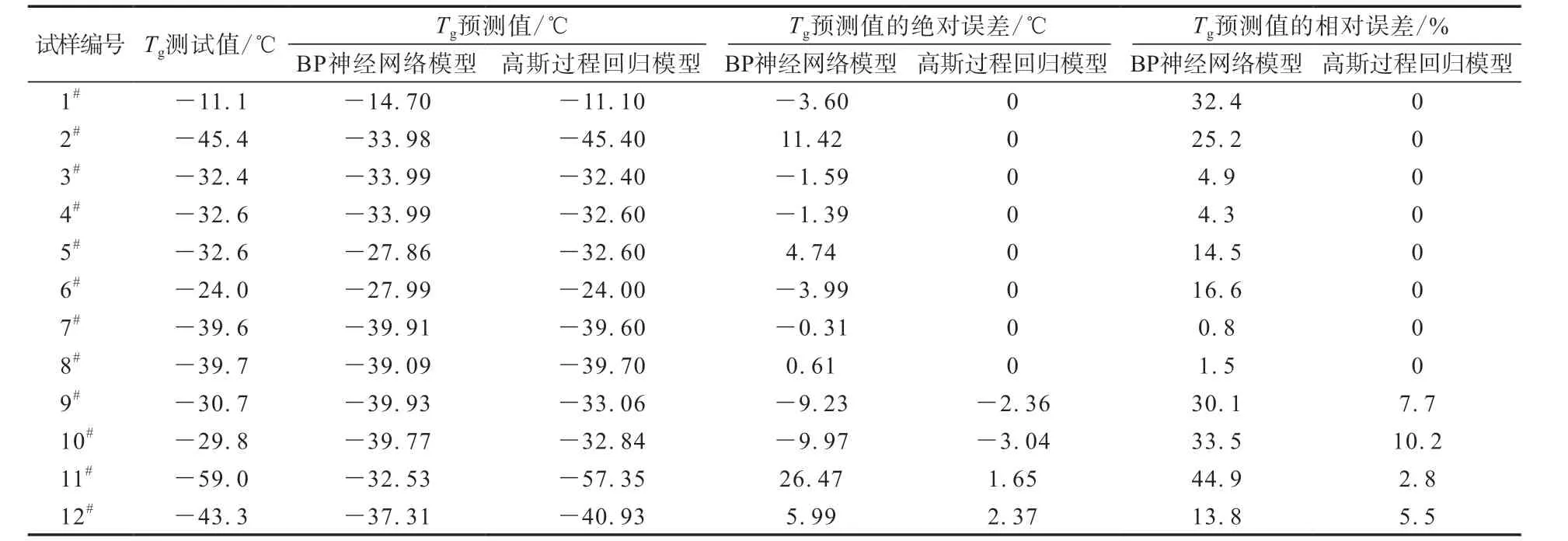
表2 SSBR的Tg测试数据和训练数据输出结果Tab.2 Testing data and train data output results of SSBR

为了了解2种模型的有效性和泛化性，对苯乙烯含量为5%～45%和丁二烯含量为24%～78%的SSBR的Tg进行预测，在设定范围内均匀采取40 000组含量值作为输入，求高斯过程回归模型和BP神经网络模型对应预测的Tg，并将预测结果绘制成3D图像，如图1和2所示。

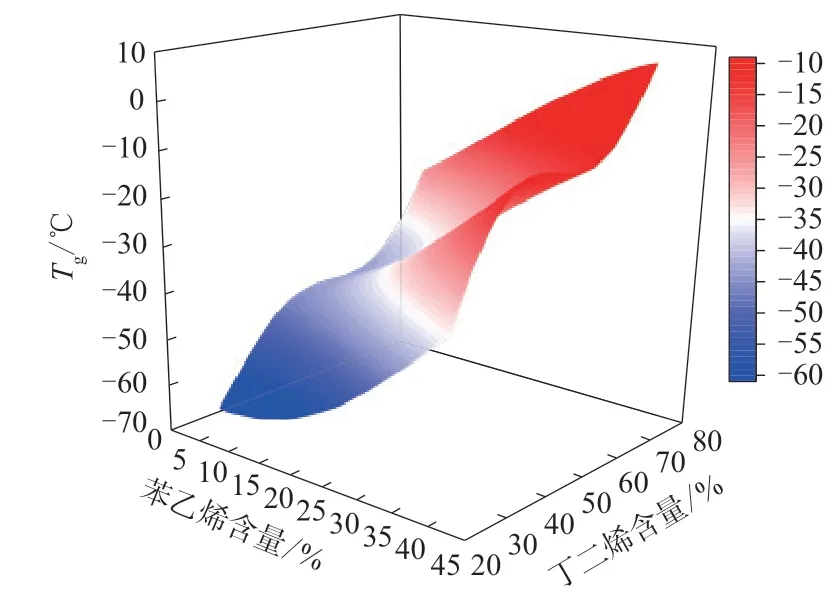
图1 高斯过程回归模型预测SSBR的Tg的3D图像Fig.1 3D image of Tg of SSBR by Gaussian process regression model

从图1可以看出，SSBR的Tg与苯乙烯和丁二烯含量的有关。在苯乙烯含量不变时，Tg随丁二烯含量增大而升高；在丁二烯含量不变时，Tg随苯乙烯含量增大而升高。高斯过程回归模型的输出结果与试验数据分析结果[15]一致，这也证明了该模型的可靠性和有效性。

从图2可以看出，BP神经网络模型预测的三维曲面不符合已知的映射关系。根据BP神经网络的特性推想模型效果不佳的原因是训练数据过少，从而BP神经网络中的参数训练不完全。

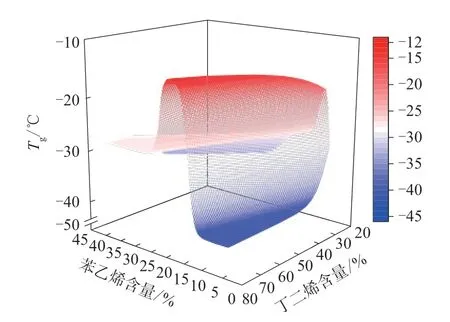
图2 BP神经网络模型预测SSBR的Tg的3D图像Fig.2 3D image of Tg of SSBR by BP neural network model

3 结论

（1）通过实例数据分析表明，高斯过程回归建立的SSBR的Tg预测模型切实可行，还可对一定范围内苯乙烯和丁二烯含量对SSBR的Tg的影响进行定性和定量分析。

（2）与BP神经网络模型相比，高斯过程回归模型解决小样本问题具有优越性，可为更多复杂耗时的试验数据预测提供有效解决方案。

（3）高斯过程回归模型可通过添加更多Tg数据，即通过增加学习数据，进一步提高模型的预测精度和可靠性。