基于改进DnCNN 的混合震源数据分离研究
张翠军, 胡家昕, 魏亚杰, 王振凯, 王承伟, 曹静杰
河北地质大学 a. 图书馆, b. 人工智能与机器学习研究室, c. 信息工程学院, d. 京津冀城市群地下空间智能探测与装备重点实验室, e. 河北省战略性关键矿产资源重点实验室, 河北 石家庄 050031
0 引言
传统勘探采集过程中, 邻炮间通常设置足够大的时间间隔以规避反射信号对检波器的交叉干扰, 导致开展高密度采集时, 耗时长、 效率低。 混合震源采集技术允许反射信号之间相互叠加, 提高了采集效率,但引入了混合震源叠加噪声, 需要进行混合震源分离以便后续处理[1]。
传统混合震源分离技术主要基于滤波方法或基于稀疏反演方法。 在滤波方面, 韩立国等[2]结合多级中值滤波和曲波变换, 提出多时域迭代去噪的混叠噪声压制方法, 实现了混合震源分离; 魏亚杰等[3]提出基于脉冲检测的方法, 使得在震源激发时间范围较小时也能成功将其分离。 在稀疏反演方面, Lin 等[4]将曲波域和离散小波域作为稀疏域, 在混合震源采集中应用压缩感知理论, 实现混合震源分离; Bagani等[5]通过基于求解线性反问题的波场分离方法分离混合震源。
近年来, 深度学习(Deep Learning) 技术发展迅速, 在计算机视觉领域表现出优越性能, 将其应用于地震数据处理和解释环节是地震勘探智能化的发展趋势[6]。 2016 年, Zhang 等[7]针对随机高斯噪声提出降噪卷积神经网络 (Denoising Convolutional Neural Network, DnCNN) 模型, 能够提取出含噪图像中的随机噪声或有效信号, 以达到有效降噪的目的。 高好天等[8]将DnCNN 运用于地震数据降噪, 验证了去除图像中随机噪声的网络模型, 同样适用于去除地震数据中的随机噪声, 与针对有效信号特征进行学习所得模型相比, 针对噪声特征进行学习所得模型的降噪效果较好。 Sun 等[9]通过卷积神经网络 (Convolutional Neural Network, CNN) 对混叠噪声进行压制, 模型在有效信号弱、 混叠噪声强的恶劣情况下仍能保持较好的降噪效果。
因深度学习模型DnCNN 针对加性高斯随机噪声具有良好的压制效果, 鉴于混叠噪声与随机噪声相似的加性特点, 尝试将DnCNN 应用于混合震源分离。针对DnCNN 模型在训练过程中频繁出现过拟合、 损失曲线大幅震荡等问题, 引入神经元失活机制和混合空洞卷积机制对其进行改进, 提出一种解决混合震源分离问题的改进DnCNN 模型。
1 方法原理
1.1 混叠噪声去噪原理
混叠噪声属于加性噪声, 含加性噪声的数据dirty的构成如式1 所示。

其中,clean为未受噪声影响的干净数据, 论文称之为有效信号;noise为噪声数据。
对于含加性噪声的数据, 一般通过数学方法直接或间接提取有效信号。 论文采取间接提取有效信号的方式, 其先提取出含噪信号中的噪声, 再用含噪信号减去噪声, 得到清晰的有效信号。
1.2 DnCNN 模型简介
DnCNN 模型针对高斯随机噪声提出, 以含噪数据作为输入, 以有效信号或者噪声作为输出。 网络共17 层, 均为卷积核大小为3×3 的卷积层, 层与层之间设置批量归一化[10]操作, 并设置从输入层连接输出层的残差通路[11], 具体结构如图1 所示。
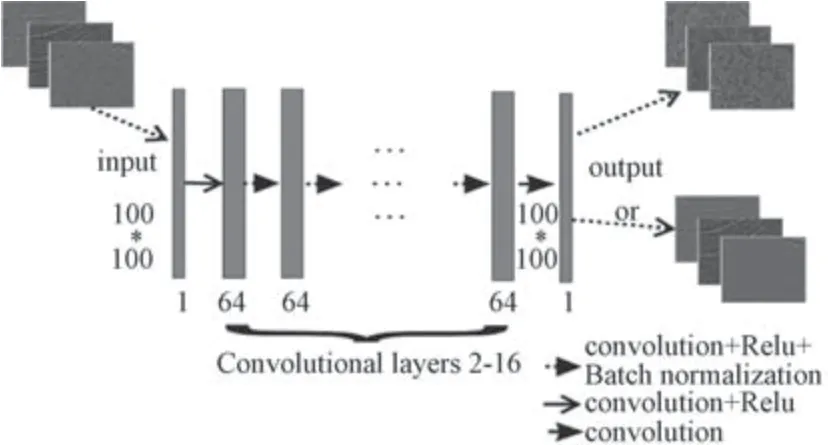
图1 DnCNN 模型示意图[8]Fig.1 Schematic diagram of DnCNN model
2 基于改进DnCNN 的混合震源分离
2.1 改进DnCNN 模型2.1.1 失活机制
DnCNN 模型层数较多, 而训练所使用的数据集规模较小, 极易造成过拟合问题, 即模型没有学习到训练数据的潜在特征分布, 而是记录下了训练数据的全部信息, 导致模型健壮性差、 泛化性差。 训练过程中过拟合直接表现为模型的训练误差损失远低于验证误差损失, 二者曲线不能良好贴合。
为了防止过拟合现象, 通常的解决方法有增强训练数据、 降低模型复杂度、 正则化 (Regularization)[12]等。 失活机制(Dropout)[13,14]也为解决过拟合问题而提出, 训练过程中使用失活机制的网络层会随机截断该层部分神经元的前向传播通路, 减弱或消除神经元间存在的相互作用, 使模型对某些强烈的局部特征依赖降低[15], 以提高其健壮性与泛化性。论文在模型固定、 数据增强的情况下, 在DnCNN 网络中隐藏层之间的连接处加入失活机制。 失活机制的示意图如图2 所示。

图2 失活机制示意图Fig.2 Schematic diagram of Dropout
2.1.2 混合空洞卷积
DnCNN 使用3×3 大小的卷积核, 感受野有限,使得模型对于全局信息把握不足, 影响最终降噪结果, 论文引入空洞卷积 (Dilated Convolution)[16]以提高模型的感受野。 空洞卷积相较于普通卷积, 引入“扩张率” 参数, 其在保持参数量不增加的情况下,使得感受野扩大, 示意图(以扩张率=2 为例) 如图3 所示。

图3 空洞卷积示意图Fig.3 Schematic diagram of Dilated Convolution
空洞卷积在提高感受野的同时, 会损失连续的特征信息, 从计算层面看, 原3×3 大小的卷积核,在扩张率为2 的情况下, 该卷积核覆盖的感受野达到了5×5, 但真正参与计算的像素数目为9, 即有16 个像素被忽视, 使得该计算过程中丢失了64%的有效信息。
当连续使用具有相同扩张率的空洞卷积时, 会引起网格效应(The Gridding Effect)[17], 即前向传播过程中, 因参与计算的像素间隔相同, 使得某一层得到的计算结果来自上一层完全独立、 没有相互依赖的像素集合, 且其余大部分像素并不会随着层数的增加而参与计算, 最终导致其有效信息完全丢失。 网格效应的示意图如图4 所示(以扩张率=2 为例)。

图4 网格效应(扩张率=2) 示意图Fig.4 Schematic diagram of The Gridding Effect (dilatation rate=2)
为解决网格效应带来的问题, 以混合空洞卷积(Hybrid Dilated Convolution, HDC) 机制保证特征的连续性。 HDC 机制通过在连续的数层中依次设置逐步增加的扩张率, 使得其最后一层的感受野中不存在“空洞”, 以确保全局信息的获取。 论文将连续三层卷积层作为一个HDC 模块, 分别设置扩张率为1、 2、3, 其示意图如图5 所示。

图5 HDC 模块示意图Fig.5 Schematic diagram of Hybrid Dilated Convolution Module
2.1.3 批量归一化
批量归一化(Batch Normalization, BN) 是一种规范化方法, 针对大型深层网络在训练时出现的收敛速度慢、 梯度消失等问题提出, 其思想源于图像预处理环节中的“白化” (Whitening) 操作, 即将输入图像的像素值分布变换到均值为0、 方差为1 的正态分布,以保证图像像素值的分布更加均匀, 而不是大部分像素都集中在一个有限的(如高曝光的图像会整体呈现出一种偏亮白的不饱满色调) 范围内。 白化操作效果如图6 所示。

图6 白化操作效果Fig.6 Whitening operation
深层网络在训练过程中, 数据的分布情况会不可避免地发生偏移或者受到扰动, 随着网络深度加深,偏移或扰动的影响可能会逐步增大, 数据的整体分布会趋向于激活函数取值区间的上下界, 从而导致反向传播过程中出现梯度消失等问题, 使得训练的收敛速度趋于缓慢。 批量归一化参考白化操作, 将每一层隐藏层都视为下一层的输入层, 每一层的前向传播进行到激活函数之前, 通过批量归一化操作将特征图的数据分布变换到均值为0、 方差为1 的标准正态分布,消除数据分布偏移的影响。 批量归一化的具体操作如算法1 所示。

算法1: Batch Normalization输入: 一个小批量的样本集合B B = {x1,..., xm} ;需要学习的参数:γ, β输出:{yi = BNγ, β(xi)}1. μB ← 1 m ∑m i=1xi / /小批量平均值2. σ2B ← 1 m ∑m i=1(xi - μB)2 / /小批量方差^3. xi ← xi - μB σ2B + ε/ /归一化4. yi ←γxi^+ β ≡BNγ, β(xi) / /调节
2.1.4 改进DnCNN 网络结构
改进DnCNN 模型以含噪数据作为输入, 噪声作为输出。 输入层接受单通道的地震数据, 数据经由卷积核大小为3×3、 扩张率为2 的空洞卷积层, 生成64通道特征图。 输入层得到的特征图送入HDC 模块,HDC 模块内由连续三层扩张率分别为1、 2、 3 的空洞卷积层组成, 相邻层间进行批量归一化和ReLU 激活, 其输出仍为64 通道的特征图。 HDC 模块共串联10 次, 相邻模块间通过批量归一化提高训练过程稳定性, 再由ReLU 激活, 并使用Dropout 机制随机抑制部分神经元的前向传播以减少过拟合现象。 经过10次HDC 模块的计算, 数据由卷积核大小为3×3 的输出层将通道数从64 合并为1。 网络采用残差机制, 从输入层连接输出层, 使得网络易于优化, 缓解深度增加时导致的梯度消失问题。 改进后的DnCNN 示意图如图7 所示。

图7 改进后DnCNN 示意图Fig.7 Schematic diagram of Improved DnCNN
2.2 实验及结果分析
论文将空洞卷积、 失活机制以及混合空洞卷积模块分别融入DnCNN 模型, 对混叠噪声数据的特征进行学习, 并将训练完毕的模型运用于测试数据进行混叠噪声降噪, 对比、 分析其降噪结果, 实现混合震源数据分离。
2.2.1 实验环境
论文实验所使用的硬件环境和软件环境如表1 所示。

表1 实验软硬件环境信息Table 1 Information of experimental software andhardware environment
2.2.2 超参数设置
实验训练所用patch 分辨率设置为100×100, 数目设置为9 000, 其中89%作为训练集, 11%作为验证集; batchsize 设置为64; 最大迭代次数设置为180;初始学习率设置为0.000 1, 当迭代次数分别达到40、90 和110 时, 学习率均降为前一轮的1/10。
实验采用Adam 优化器[18]在训练过程中进行反向传播[19]以更新模型参数。
2.2.3 损失函数
损失函数为均方误差(Mean square error, MSE),其计算方法如式2 所示。
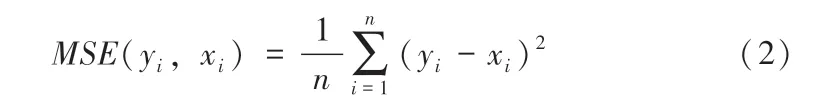
其中,n为一个batch 中使用的patch 数量;xi和yi分别为该batch 中第i个patch 的降噪结果及标签。
2.2.4 评价指标
实验结果的评价指标为信噪比(Signal to Noise Ratio, SNR)、 峰 值 信 噪 比 (Peak Signal to Noise Ratio, PSNR)、 平方误差(Square Error, SE), 计算方法分别如式3、 式4 和式5 所示。

其中,x为某样本经模型降噪后的结果,y是其对应的有效信号标签。
2.2.5 实验结果展示及分析
实验采用某海域一套实测单震源数据(100 个震源、 100 个检波器) 作为测试集, 其含有100 个样本。设置五种算法模型(1) DnCNN; (2) DnCNN+Dilated Convolution; (3) DnCNN+Dropout; (4) DnCNN+Dilated Convolution+Dropout; (5) DnCNN+HDC+Dropout, 分别计算测试集降噪结果的信噪比平均值、峰值信噪比平均值、 有效信号标签和降噪结果的平方误差平均值, 对比结果如表2 所示。
从表2 中可以看出, 在保持学习率一致的情况下, 模型(1) 即DnCNN 模型训练完毕后, 在测试集上的混叠噪声降噪结果信噪比平均值达到了15.98、峰值信噪比平均值达到了35.93, 二者均为5 个模型测试结果中最低值; 平方误差平均值为30.57, 是5个模型测试结果中的最大值。

表2 五种算法模型降噪结果对比Table 2 Comparison of denoising results of 5 methods
模型(2) 将DnCNN 模型15 层隐藏层中大小为3x3、 扩张率为1 的普通卷积替换为大小为3x3、 扩张率为2 的空洞卷积, 卷积操作的感受野增加。 相较于模型(1), 模型(2) 的信噪比和峰值信噪比的平均值略有提升、 平方误差平均值减小, 说明其整体降噪效果得到小幅提升。 模型(2) 连续使用具有相同扩张率的卷积操作所引起的网格效应, 在计算过程中丢失了大量的数据特征, 且参与计算的信息也不具有连续性, 使得降噪效果虽有提升, 但提升幅度不大。
模型(3) 保持DnCNN 卷积操作不变, 在15 层隐藏层之间加入了失活机制, 随机将部分神经元的前向传播截断, 该操作虽然增加了训练过程的随机性,但有效降低了过拟合及曲线震荡出现的可能性, 其最终测试结果信噪比平均值较模型(1)、 (2) 有明显提升, 且平方误差平均值降低显著, 是五种模型测试结果中的最小值。
模型(4) 同时结合模型(2)、 (3) 两种改进策略, 但实际测试结果显示信噪比、 峰值信噪比都受到较大影响, 并且平方误差增大, 造成这种结果的原因是特征图信息的连续性受到了较大的破坏。 空洞卷积和失活机制均会对数据特征的连续性造成一定破坏,两者分别单独使用时, 空洞卷积可以增加卷积核的感受野、 失活机制可以在一定程度上消除神经元间不利的相互作用, 此时两者单独对降噪效果的增益能够弥补对信息连续性破坏产生的影响; 两者搭配使用时,对特征的连续性产生的破坏效果相互叠加, 影响进一步增大。 实验结果表明, 空洞卷积和失活机制搭配使用时, 模型学习能力降低, 降噪效果变差。
模型(5) 通过混合空洞卷积机制, 有效缓解了连续使用具有相同扩张率的空洞卷积所引起的网格效应, 保护了数据特征的连续性, 信噪比平均值、峰值信噪比平均值均得到提升, 其中关键指标信噪比平均值达到了17.36, 是5 个模型结果中的最高值, 峰值信噪比和平方误差也保持在较好的水平,说明模型(5) 相较于其他模型, 降噪效果得到了明显提升。
5 个模型的损失曲线如图8 所示。 图8 为5 种算法的损失曲线图, 因第1 轮迭代中模型的损失误差都较大, 会拉升图像纵轴范围尺度, 影响细节展示, 所以将其隐藏, 只展示第2 轮及以后的损失曲线变化情况。 从图8 (1) 中可以看出, DnCNN 训练过程中会出现强烈的损失曲线震荡问题, 且经多次反复实验,损失曲线震荡、 过拟合等情况出现概率极高, 对最终训练效果影响较大。 图8 (2) 中, 空洞卷积略微降低了损失曲线震荡的幅度, 但震荡情况依然严重, 且存在过拟合问题(红色的验证误差曲线在震荡处远高于绿色的训练误差曲线)。 图8 (3) ~ (5) 中, 失活机制的引入使得曲线震荡问题得到明显改善, 过拟合发生的可能性也大大降低, 在大致相同的范围下(取纵向坐标0~1 000 范围), (3) 和(4) 仍有小幅震荡, 论文所提改进DnCNN 模型的损失曲线则更加平滑, 下降趋势稳定且没有过拟合现象发生。

图8 五种算法的损失曲线Fig.8 Loss curve of 5 algorithms
从表1 中可以看出, 论文改进的DnCNN 模型测试信噪比平均值最高, 降噪效果最好, 其降噪结果如图9 所示。
图9 中, 图9 (1) 为原始含噪数据; 图9 (2)为图9 (1) 中噪声的标签; 图9 (3) 为模型提取出的噪声数据; 图9 (4) 为图9 (1) 减去图9 (2) 所得有效信号的标签; 图9 (5) 为图9 (1) 减去模型提取的噪声图9 (3) 所得的降噪结果。 可以看出,论文改进模型对于含噪数据中的混叠噪声预测准确,降噪效果明显, 并且能够较好地保护有效信号。
混合震源数据分离结果如图10 所示。
图10 中, 图10 (1) 为含噪数据, 即混合在一起的有效信号; 图10 (2) 为图10 (1) 中的一个有效信号标签; 图10 (3) 为论文改进模型分离所得结果。 可以看出, 论文改进模型对于有效信号的保护效果较好, 分离结果中有效信号完整, 样本中靠下部的弱信号也清晰可见, 被削弱的程度很小, 有利于后续数据处理和解释。

图10 分离结果Fig.10 Deblending result
3 结论
论文通过引入HDC 模块和Dropout 对DnCNN 模型进行改进, 并将改进后的模型用于混叠噪声降噪,最终实现混合震源数据分离。 改进后的DnCNN 模型对于地震数据中含有的混叠噪声具有良好的压制效果:一方面, HDC 模块通过连续增加的扩张率保证了全局信息的获取, 一定程度上保护了特征的连续性; 另一方面, Dropout 抑制了神经元间的相互作用, 提高了训练过程的稳定性。 综上所述, 改进后的DnCNN 模型对混叠噪声预测准确, 降噪效果明显, 地震数据信噪比得到提升, 使得在混合震源数据分离阶段能够较好地保护有效信号, 一定程度上避免其受到削弱。

