基于频域互相关的机器鱼双曲线质心定位仿真

刘力卿，王 伟，张 弛，马小光

(1. 国网天津市电力公司电力科学研究院，天津 300384；2. 国网天津市电力公司设备管理部，天津 300384)

1 引言

变压器在电网中承担着传输和转换电能的作用，截至2017年底，国家电网中110kV及以上电压等级的变压器已经超过30000台，总装机容量达3400000MVA[1]。变压器受工作环境、运行工况等因素的影响，在运行过程中难以避免会发生故障。随着智能电网的发展，变压器运行的安全性和可靠性显得尤为重要。

目前，变压器内部故障的主要检测方法是局部放电监测和油中溶解气体分析法(Dissolved Gas Analysis，DGA)[2-5]。随着人工智能和微型机器人技术的进步，采用微型机器鱼对变压器进行巡航检测，可以实现变压器故障更直观、更快速分析和定位[6]。机器鱼在巡航过程中需要实时反馈自身在变压器油中的位置坐标，然后根据控制指令到达指定位置完成巡航检测任务。因此，机器鱼定位是其完成巡航任务的首要问题。常用的机器人定位技术主要包括：GPS、电磁雷达、惯性陀螺仪、视觉相机等方法[7-12]。但是，由于变压器由金属外壳完全密封，内部充满变压器油，是一个封闭、黑暗的空间，外部GPS信号难以进入，并且变压器油对电磁雷达波衰减大，这些特点极大的增加了定位的难度，常规的定位方法具有一定的局限性。目前针对变压器机器鱼这样特殊应用场景的定位研究较少，参考深海水下机器人的定位技术，采用声学定位方法，提出了一种基于超声阵列频域互相关的机器鱼双曲线质心定位方法，该方法具有信号在液体中衰减小、无累积误差、信号发射和接收方便等优势。

2 变压器和微型机器鱼结构

油浸式变压器结构如图1所示，主要包括变压器外壳、内部绕组和变压器油等部分。

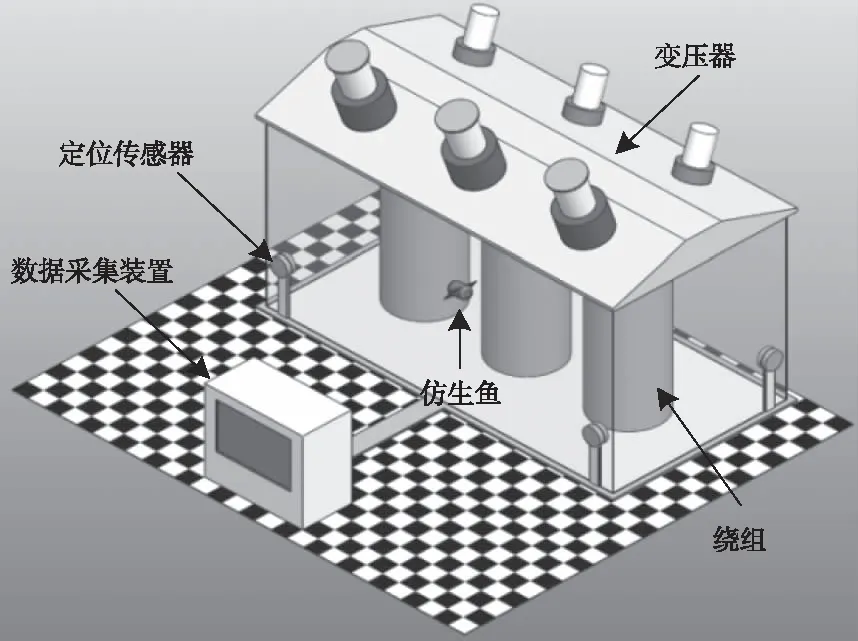
图1 变压器结构示意图

微型机器鱼对变压器进行检测的过程包括：将机器鱼从变压器注油孔装入变压器油中，机器鱼根据自身位置和控制指令，对变压器内部进行巡航检测，通过机器鱼体内安装的传感系统对变压器的内部组件进行感知和检测。机器鱼安装有超声波发射装置，变压器油中布放超声接收阵列，通过鱼体超声发送、阵列信号接收，并且结合声波传播特性和信号处理算法，可以实现机器鱼在变压器油中的准确定位。机器鱼结构如图2所示。

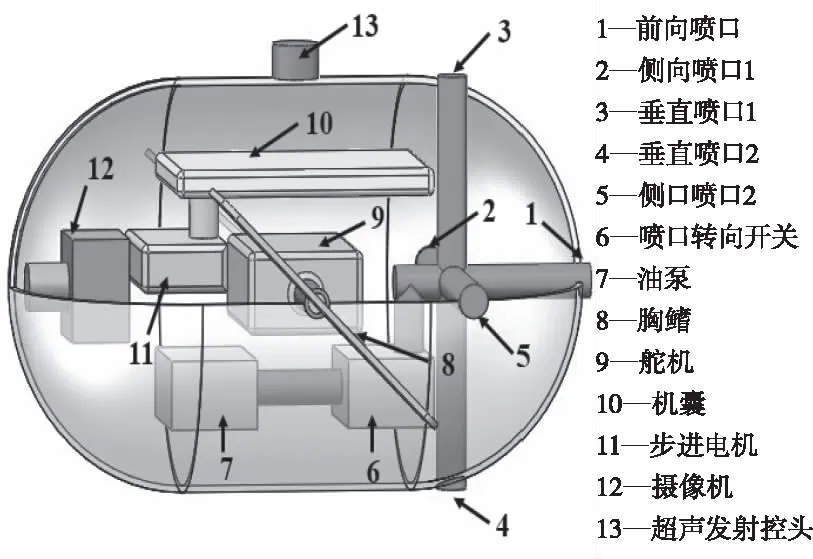
图2 变压器微型机器鱼示意图

3 机器鱼定位原理

变压器为三维立体结构，准确定位机器鱼的位置需要确定机器鱼的水平坐标(X轴坐标和Y轴坐标)、深度(Z轴坐标)，如图3所示。

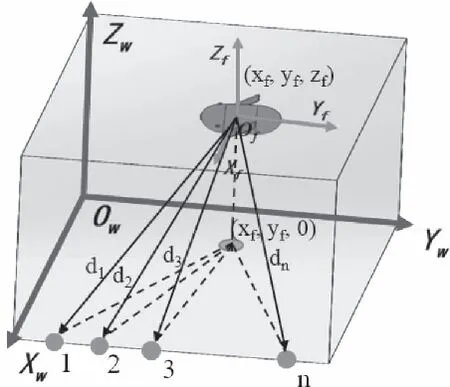
图3 机器鱼位置示意图

假设机器鱼的坐标为(xf，yf，zf)，线性传感器阵列所在深度为zs，阵列中任意传感器的坐标为(xi，yi，zs)。机器鱼体上安装有压强计，根据式(1)可以实现机器鱼深度的计算，式中P为压强，ρoil为变压器油的密度。

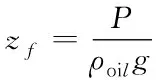
(1)

因此，机器鱼定位的主要难点在于机器鱼水平面信息(X轴坐标和Y轴坐标)的获取。因此，机器鱼的定位由三位定位转变为二维定位。定位流程图如图4所示。

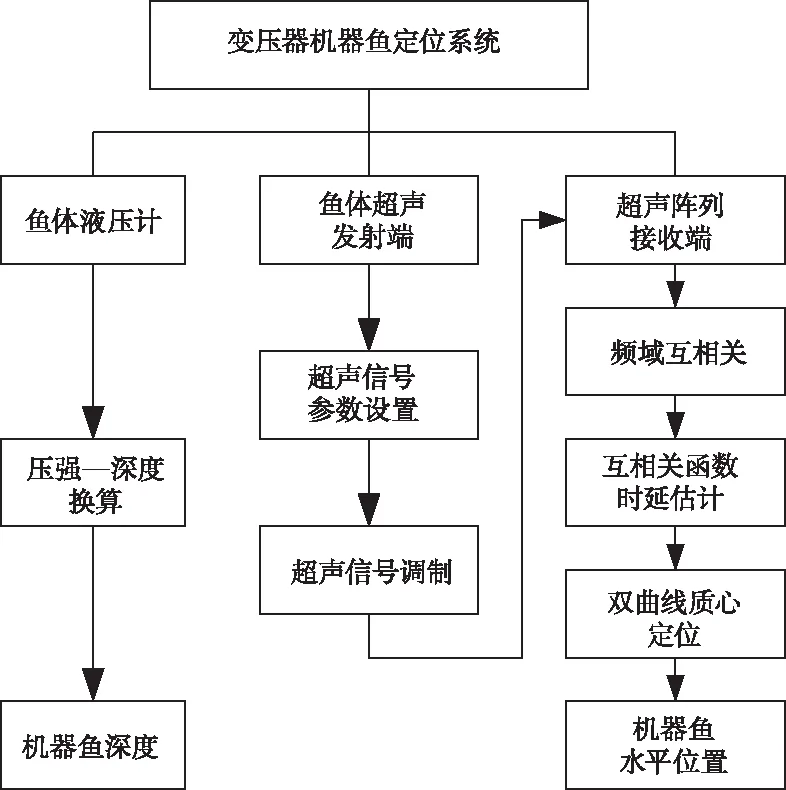
图4 机器鱼定位流程图

3.1 超声信号传播与时延估计

声波在变压器油中传播的运动方程为

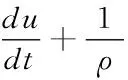
(2)

根据质量守恒定律，连续性方程可表示为

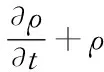
(3)

状态方程为

dp=c2dρ

(4)

公式中，u表示质点振速，p为声压，ρ为变压器油密度，c为声速，▽为拉普拉斯算子。

根据式(2-4)可以得到声波的波动方程

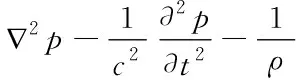
(5)

由于短时间内变压器油的密度是恒定的，因此声场中某个位置处的声压可以表示为

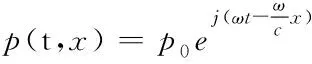
(6)

式中p0为声源处的声压，ω为角频率。

假设机器鱼发射的超声信号为s(t)，超声信号在传播过程中会受到衰减、时间延迟、噪声和反射等因素的影响，因此，传感器接收到的信号可以表示为

(7)

式中di为传播距离，Di为时间延时，ni(t)为噪声，ri(t)表示反射信号，由于采用的超声信号频率较高，反射信号可以忽略不计。接收的超声信号的信噪比(SNR)定义为

(8)

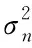
机器鱼发射的超声信号经过不同的传播路径到达超声阵列，互相关时延估计模型如下所示

Rx1x2(τ)=E[x1(t)x2(t+τ)]

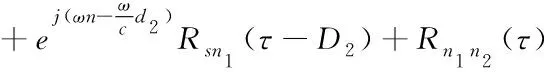
(9)

式中，Rss[τ-(D1-D2))为有效信号(即衰减和延时的信号)的互相关函数，Rsn1(τ-D2)和Rsn2(τ-D1)为有效信号和噪声的互相关函数，Rn1n2(τ)为噪声和噪声的互相关函数。

一般情况下，信号与噪声、噪声与噪声之间是弱相关或不相关，即

Rsn1(τ-D2)=Rsn2(τ-D1)=Rn1n2(τ)≈0

(10)

因此，互相关函数可以简写为

(11)

频域互相关计算公式为

Rss[τ-(D1-D2)]

(12)

式中，S1(ω)和S2(ω)为信号s1(t)和s2(t)经傅里叶变换得到的频谱，*表示复共轭。

通过对互相关函数进行峰值检测，峰值对应的横坐标即为时间延迟，如式(13)所示。

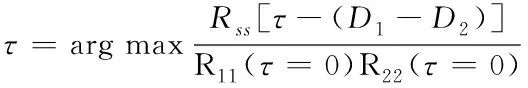
(13)

式中，R11(τ=0)和R22(τ=0)分别表示信号1和信号2的自相关函数在τ=0时的取值。频域互相关计算流程如图5所示。

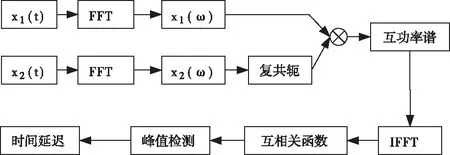
图5 频域互相关计算流程

3.2 双曲线质心定位算法

目标搜索和定位中常用的算法包括：圆形(或圆球)算法和双曲线(或双曲面)算法[13，14]。如果已知目标与传感器之间的距离(即圆的半径)，采用圆算法可以进行定位，根据不同传感器信号绘制多个圆形，圆形交点即为目标点。但是实际应用中往往无法知道目标与传感器的之间距离，这种情况需要根据不同传感器的信号，采用双曲线算法反推计算目标点的位置。

假设平面上机器鱼的坐标位置为M(xf，yf)，阵列中2个超声传感器的坐标为F1(x1，y1)和F2(x2，y2)。以传感器的连线方向为x轴，中垂线方向为y轴，建立直角坐标系。基于声波在材料中沿最小能量衰减路径传播的原理，机器鱼到传感器的距离可以通过声速与时间延迟的乘积计算获得，如式(14-16)所示

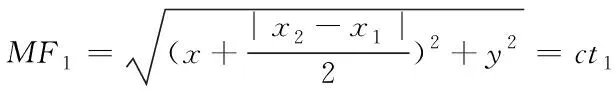
(14)

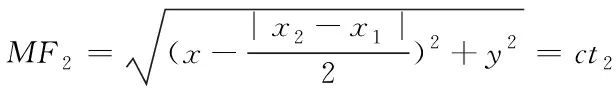
(15)

|MF1-MF2|=cΔt

(16)

式中，Δt为根据式(3-4)计算的时间延迟，c为油中的声波速度。

根据几何原理可知，如果目标源到2个传感器的距离差大于0且小于传感器之间的距离，则目标源在以传感器为焦点的双曲线上。双曲线定位原理如图6所示。

图6 双曲线定位原理

采用2个超声传感器只能得到一组双曲线，因此，如果需要准确计算出目标源的坐标，至少需要3个以上的传感器组成超声阵列，阵列中多组双曲线的交点即是目标源的位置。由于噪声的存在，双曲线一般交于多点，假设交点有m个，则双曲线的质心计算公式如下

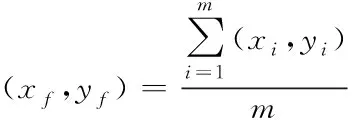
(17)

4 机器鱼定位仿真验证

4.1 变压器二维模型

变压器截面二维模型如图7所示，其中变压器长度为3.5m，宽度为1.5m，中间部分包含3个绕组，绕组直径为0.5m，绕组距离变压器上下壁面各为0.5m；线性超声阵列中包含5个传感器。

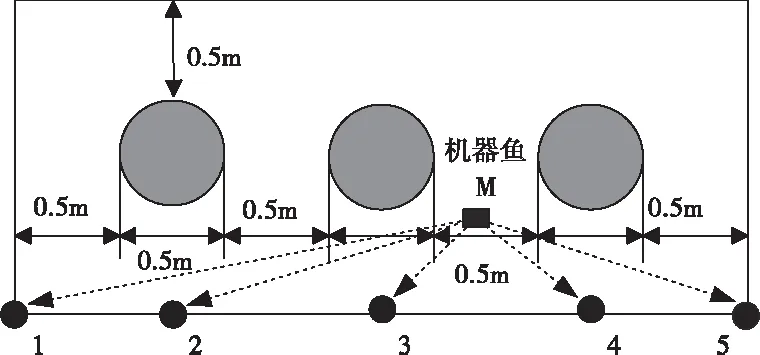
图7 变压器等比例截面模型

机器鱼在变压器中的坐标设置为(2m，0.5m)，传感器1-5的坐标设置为(0 m，0 m)，(0.75 m，0 m)，(1.75 m，0 m)，(2.75 m，0 m)，(3.5 m，0 m)。

4.2 超声发射信号和传感器接收信号

机器鱼发射的超声信号应该具有以下特点：一是具有较大的辨识度，能够和变压器中的本底噪声进行分离；二是发射的超声信号不能与变压器自身发生的故障信号相似。因此，采用调制的高斯脉冲信号模拟超声发射信号，信号中心频率设置为100kHz，采样率设置为500kHz，信号时长为1ms，高斯脉冲出现的时刻为0.5ms。模拟高斯信号的时频和频域波形如图8所示。

图8 模拟超声信号

按照3.1节超声信号在变压器油中的传播规律，发射的超声信号经过指数衰减得到不同位置传感器的接收信号，如图9所示。

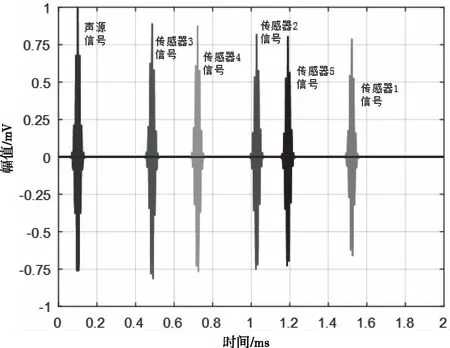
图9 传感器信号

4.3 不同信噪比的定位结果

对超声阵列接收的信号添加高斯白噪声，选择信噪比分别为10dB，0dB，-10dB来模拟不同噪声条件(低噪声、中等噪声和高噪声)。通过对阵列中不同传感器的信号进行互相关计算，得到不同信噪比条件下的时延计算结果，如图10-12所示。

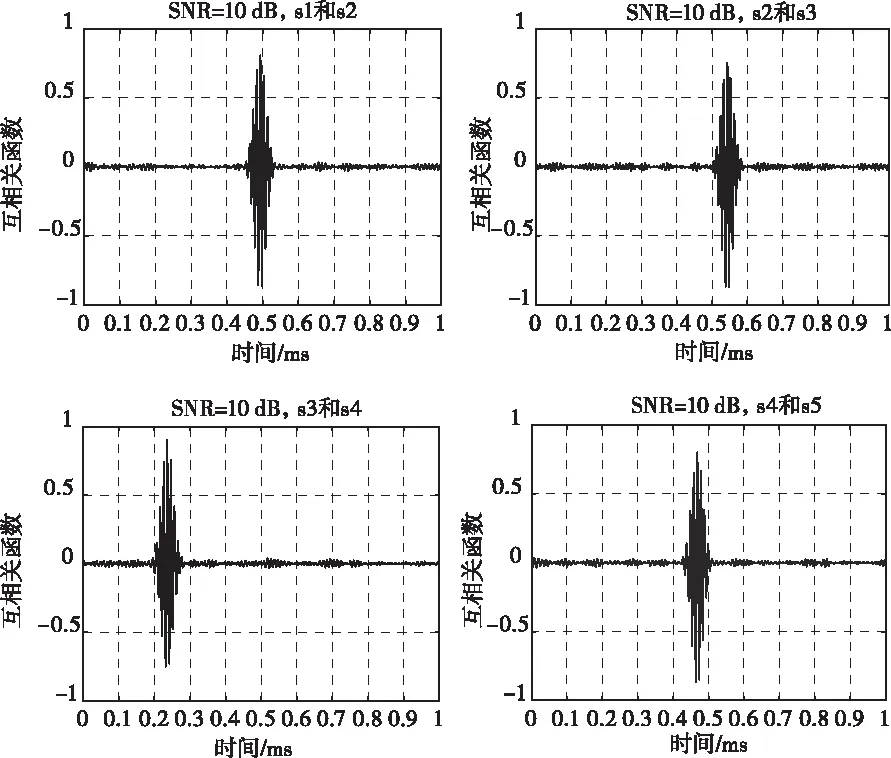
图10 互相关计算结果(SNR=10dB)

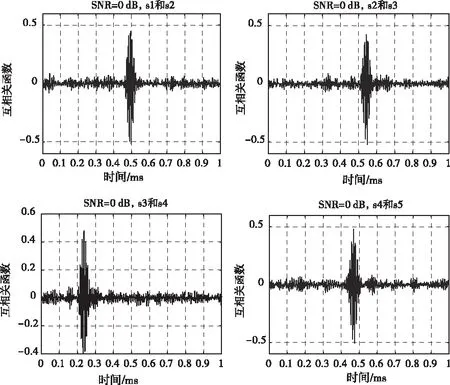
图11 互相关计算结果(SNR=0dB)

图12 互相关计算结果(SNR=-10dB)

通过比较上图可以看出，随着信噪比的降低，互相关函数曲线峰值的尖锐程度逐渐变差，相关系数逐渐变小。不同信噪比条件下相关系数结果如表1所示。

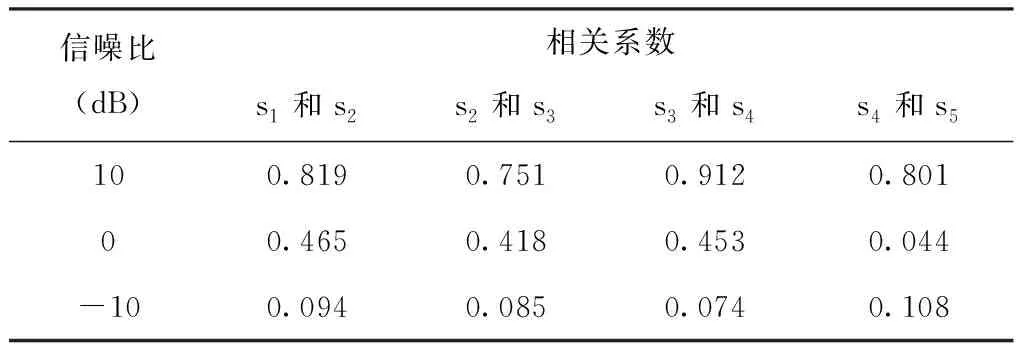
表1 不同信噪比条件下相关系数结果

通过表一纵向比较可以看出，随着信噪比的降低，每1组传感器的相关系数逐渐减小，说明了噪声的加入降低了信号之间的相关性，从而增加了时间延迟的求解难度。通过表一横向比较可以看出，不同传感器的相关系数略有差别，其中3号和4号传感器的相关系数最高，这是因为这两个传感器距离机器鱼的距离最近，信号衰减相对其它传感器较少。

采用信噪比为10dB的时间延迟结果，采用双曲线质心算法得到的机器鱼定位结果如图13所示，交点区域的放大图如图14所示。

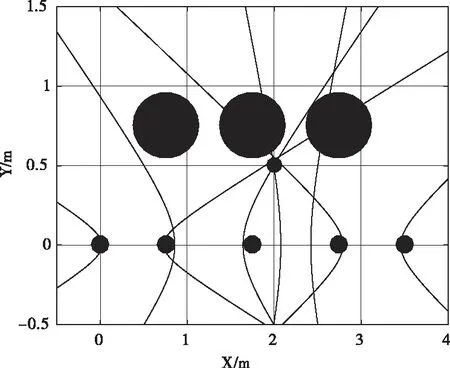
图13 双曲线定位结果

图14 交点区域的放大图

通过图13和图14可以看出：多组双曲线并没有完全交于一点，这是由于噪声的存在，定位存在一定的误差。选取交点坐标：(1.99m，0.50m)(1.98m，0.53m)(2.02m，0.54m)(2.04m，0.53m)(2.06m，0.55m)，根据式(17)求得双曲线交点的质心坐标为(2.02 m，0.53m)，与设置的机器鱼位置相比，横坐标和纵坐标的相对误差分别为：(1%，6%)，这样的定位误差已经基本满足工程应用的需要。

5 结论

针对变压器油中微型机器鱼的位置信息获取问题，本文提出了一种基于频域互相关的机器鱼双曲线质心定位方法。通过对超声信号进行快速傅里叶变换和复共轭计算得到信号的互功率谱，通过对互功率谱进行傅里叶逆变换得到互相关函数，通过对互相关函数曲线峰值检测得到时间延迟和距离信息。通过仿真比较了不同信噪声条件下的时延估计结果和双曲线定位图像，研究结果表明：所提方法能够准确获得机器鱼在变压器中的位置。