基于可靠度的复杂建筑空间结构节点连接方法

何 平，刘海亮

(扬州大学设计学院，江苏 扬州 225000)

1 引言

从古至今，人类经常面临火灾、地震等自然灾害，像1976年的唐山大地震、2008年的汶川大地震等，不仅使工程遭到恶劣的破坏，而且使人们生命财产损失惨重。建筑的安全性与抗震性是工程中的重中之重，同时也是国内外学术界和工程界一贯重视的研究课题[1]。随着我国经济飞速发展，全国各地出现许多扭曲复杂空间结构建筑，虽美观新颖，但造型施工非常复杂[2]，现有三种方法解决复杂建筑空间结构外表皮，解决方法分别为：①为达到最好的效果，可以将双曲面面板材料及支撑杆件弯曲成要设计的造型，但该方法存在造价成本及加工精度高，施工进度慢，且材料损耗严重的弊端；②若不破坏建筑的整体效果，可以采用单曲面或平面面板模拟层叠或阶梯状的方法，使用该方法的建筑具有非常强的层次感。③对于各种不规则的复杂空间曲面[3]，最常用的方法是使用三角形平面面板模拟方法，该方法具有广泛的适用性。以上三种方法都存在支撑杆件和面板材料之间产生缝隙的风险，即其紧密度低，导致面板间不共面及设计模型与真实结构存在误差等。因此复杂空间结构面临极大的技术困难，如安装繁琐、不易施工、杆件之间角度偏差大等[4]。合理有效的节点连接方法可以充分提升复杂建筑的可靠度与稳定性。

许多相关领域学者为此付出诸多努力，如姜宝龙等人为进一步提升结构节点连接稳定性，试验研究钢混凝土梁空间节点抗震性能[5]，但该方法在对建筑空间结构的可靠度和稳定性提升效果不显著；赵俊贤等人研究防屈曲支撑钢框架滑移连接节点抗震性能[6]，该方法虽抗震性比较高，但造价高，施工难度大。因此为解决现有研究复杂建筑空间结构节点抗震性低，施工难度大等问题，进一步提高其可靠度和稳定性，本文提出基于可靠度的复杂建筑空间结构节点连接方法，有效提高复杂建筑空间结构的可靠度。

2 复杂建筑空间结构节点连接方法

2.1 复杂建筑空间结构节点设计原则

将球头部署到复杂建筑空间结构的杆件连接装置的球头支撑螺杆上端，部署过程中利用螺母稳定[7]，支撑螺杆低端的螺纹同螺纹套筒上端协同，实现球头支撑螺杆的旋转控制，间接实现耳板连接组件空间位置的控制[8]。

为确保建筑空间结构外表平整，需调节耳板组件的前后位移[9]，该位移可利用旋转球头连接的支撑螺杆和加长支撑螺杆的螺纹螺向进行调节，且两个支撑螺杆的螺纹螺向需要保持相异性。

由于加工与安装的影响，会对杆件之间产生角度误差，该误差可利用增加耳板连接组件与可旋转连接耳板进行消除。为获得不同数量的杆件，可在杆件相交位置增加或减少连接耳板。通过小幅度调整支撑柱上的耳板确保球头节点连接角度误差最低化，增强施工质量[10]。

2.2 复杂建筑空间结构节点设计方案

耳板连接组件及该组件中的连接耳板构成复杂建筑空间结构杆件连接装置，其中弧形长条孔和嵌入槽组成耳板连接组件，长条孔可调整连接耳板间的夹角，连接耳板可围绕耳板连接组件转动，亦可在嵌入槽里旋转[11]。耳板连接组件又称环形嵌入槽，其由连接柱的两端分别连接耳板底座及扣盖组成[12]，连接耳板的两端的功能分别是部署和稳定。为了固定嵌入槽中的连接耳板，可采用限位螺栓的方式完成固定，但固定的前提是必须调节好连接耳板组件的位置[13]。

2.3 节点连接可靠度设计

基于可靠度的有关原理，可明确复杂建筑空间结构节点连接设计的安全系数，且该安全系数需符合目标可靠度[14，15]。目标可靠度的指标可借鉴钢结构标准，用β=2.9描述连接节点设计的目标可靠度。

复杂建筑空间结构极限承载力实际值Nbut公式为

Nbut=ΩbωAcfy

(1)

式(1)中：计算模式不确定系数与及应变强化影响系数实际值分别用Ωb与ω描述；结构核心截面面积实际值与钢材的屈服强度用Ac与fy描述。

利用复杂建筑空间结构节点连接抗力与极限承载力剖析可靠度指标，二者的分项系数为

(2)

其中

其中：参考设计值，连接抗力的分项系数用γR描述；极限承载力的分项系数用γS描述；参考均值，连接抗力的分项系数用γ0R描述；极限承载力的分项系数用γ0S描述；连接抗力的均值和设计值的比用KR描述；极限承载力的均值和设计的比用KS描述；节点连接抗力的变异系数用VR描述；极限承载力的变异系数用VS描述。

对应的设计公式为

γRRd≥γSNbu

(3)

式(3)中：节点连接抗力的设计值用Rd描述；复杂建筑空间结构极限承载力的设计值用Nbu描述。

将式(3)变成单一安全系数设计公式，则公式为

Rd≥(γS/γR)Nbu=KNbu

(4)

式(4)中：用K描述单一安全系数。

2.4 荷载类变量的概率模型

荷载类变量的概率模型公式为：

(5)

标记为N(1.06Gk，0.074Gk)，式(5)中，恒载标准值用Gk描述，其均值标准差为

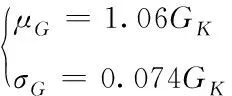
(6)

3 实验分析

以A市某复杂建筑的屋顶为研究区域，采用本文方法对该空间结构节点进行连接，该屋顶采用双层球面网壳结构，具有135.487m与17156m2的覆盖直径与表面积。全部杆件均使用圆钢管截面，最小钢管直径是110mm，最大钢管直径是198mm，节点直径最小是288mm，最大直径是574mm。在人字型钢柱柱顶上，利用边桁架进行支撑球面网壳，由腹杆连接环梁，连成的四根环梁可组成边桁架。边桁架依旧是圆钢管截面，钢管直径是458-1115mm。该结构关键节点包括铸钢节点和大直径相贯节点两种。

3.1 节点连接可靠度分析

统计该复杂空间结构选取不同圆钢管杆件及连接节点材质时螺栓和焊缝的安全系数情况，结果如表1所示。

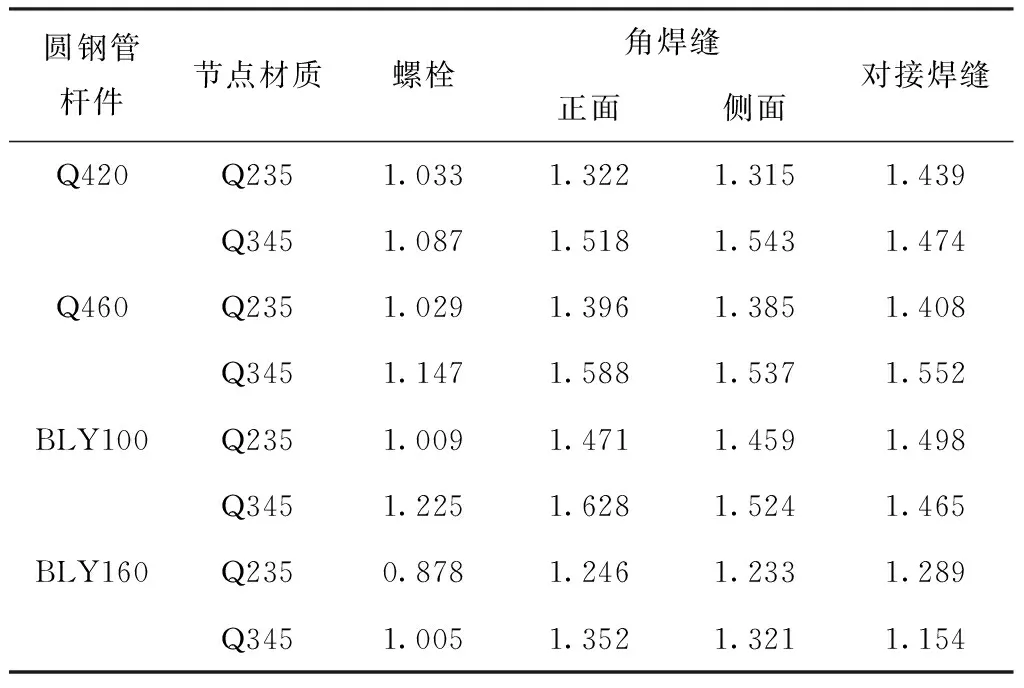
表1 安全系数K取值

通过表1可得，圆钢管杆件材质为Q420、Q460、BLY100时，结构的螺栓、角焊缝和对接焊缝的K值较高，且节点材质为Q235和Q345，对K取值影响较小，结构的可靠度较高；圆钢管杆件材质为BLY160，节点材质为Q235时，螺栓连接K值较低，正、侧面角焊缝和对接焊缝的K值相对略低，可靠性相对较差，表明此种钢材的变异性较差，导致复杂建筑空间结构节点连接可靠度降低。

通过轴压下的节点平均荷载-位移曲线，衡量本文连接铸钢和大直径相贯两种关键节点的可靠性。结果如图1所示。

图1 关键节点平均荷载-位移曲线

从图1中可看出，两种关键节点的荷载-位移曲线较为相似，大约在位移0mm-12mm范围内，两种关键节点的荷载值均呈大幅度增长趋势，之后逐渐平稳，未产生明显的屈服点，实验表明，两种关键节点的荷载-位移曲线性质基本相同。

3.2 初始缺陷大小对不同厚度网架可靠度的影响

研究不同网架厚度以及初始缺陷大小对网架可靠度指标的影响，衡量空间结构节点的可靠性。分析不同初始缺陷下，0.3m-3.5m九种不同的网架厚度的网架的可靠度指标的变化曲线，结果如图2所示。

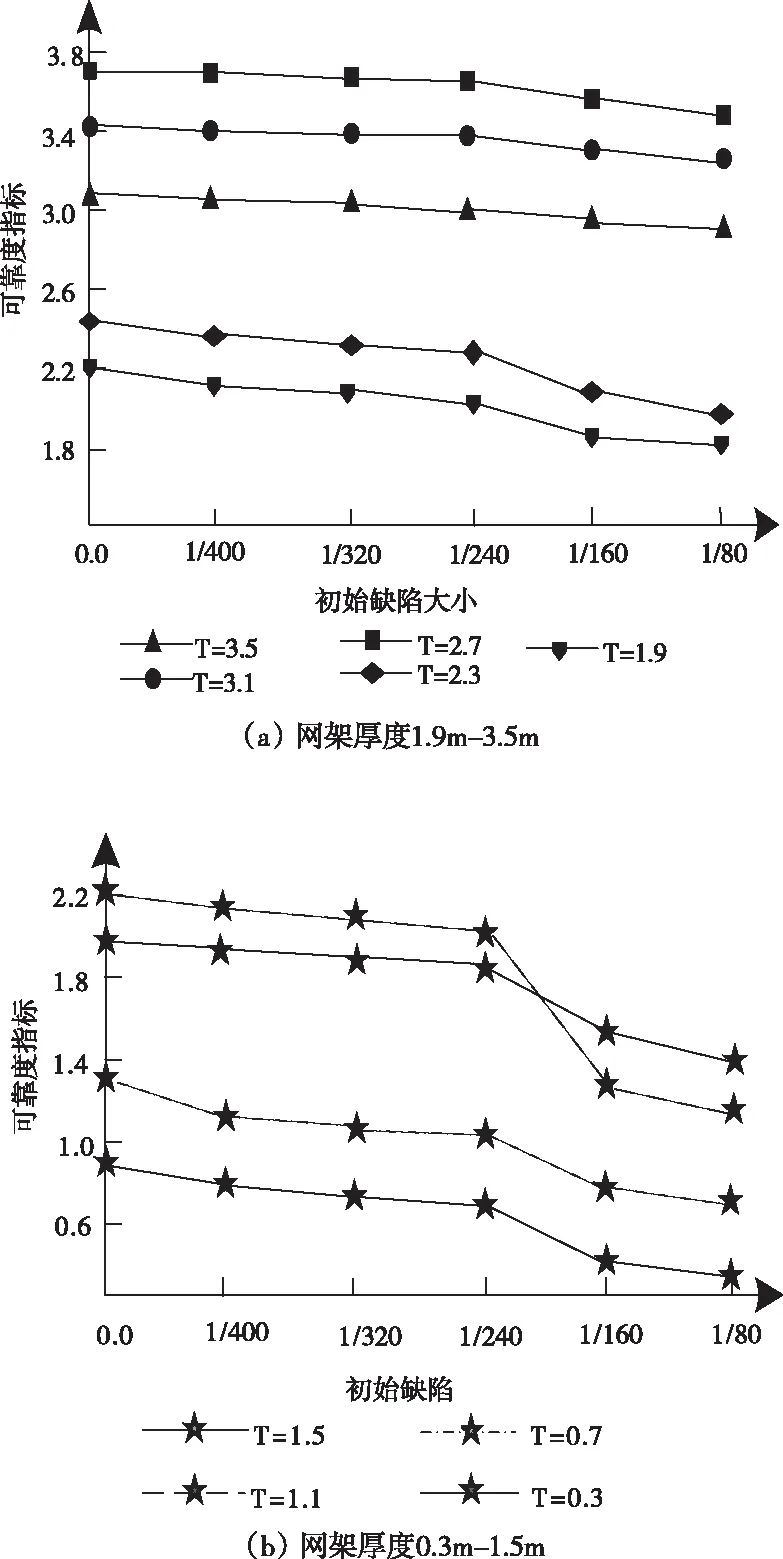
图2 初始缺陷对网架可靠度指标的影响

由图2可得，该九种厚度网架的可靠度指标均随着初始缺陷的增加而逐步呈现下降趋势；特别是初始缺陷在1/240-1/160区间内，可靠度指标下降速度最快；当网架厚度T=3.5m、3.1m、2.7m时，随着初始缺陷的增加，可靠度指标虽逐渐变小但变化趋势并不明显；当网架厚度T=1.1m、0.7m、0.3m时，随着初始缺陷的增加，可靠度指标明显降低，实验表明，网架厚度越小，对初始缺陷的敏感度越高。

3.3 随机变量相关系数对不同厚度网架可靠性的影响

图3及图4为0.3m-3.5m九种不同网架厚度的网架的可靠度指标随荷载以及弹性模量相关系数的变化曲线，本节研究基于不同网架厚度，荷载与弹性模量相关系数对网架可靠度指标的影响规律。

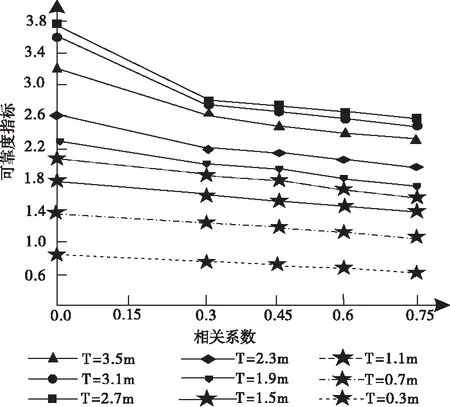
图3 荷载相关系数对可靠度的影响

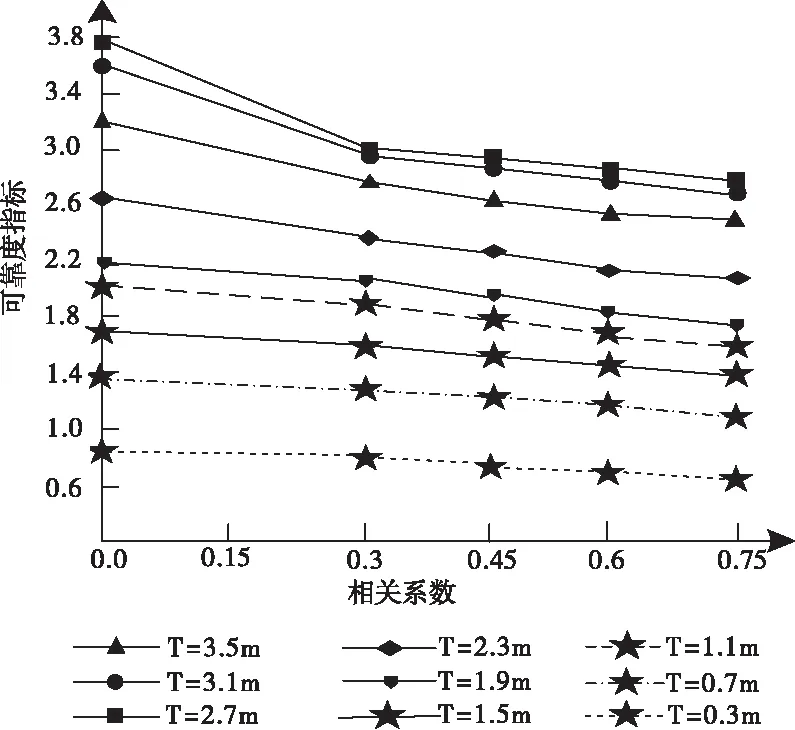
图4 弹性模量相关系数对可靠度的影响

从图3及图4中可看出，随着荷载及弹性模量相关系数的增大，网架可靠度呈现下降趋势，当相关系数在0-0.3区间时，可靠度指标下降速度最快；当相关系数在0.3-0.75区间时，可靠度指标下降速度逐渐减缓。当网架厚度为T=3.5m、3.1m、2.7m时，随着相关系数的增加，可靠度指标下降速度比较明显；实验表明，可靠度指标随着荷载、弹性模量相关系数的增加而减少，且网架厚度越大，可靠度指标下降速度越快。

3.4 大直径相贯节点可靠度分析

为研究该复杂建筑空间结构大直径相贯节点的失效应力值是否在安全概率的弹性范围内，现设置结构的设计屈服强度为340MPa，表3为大直径相贯节点可靠性分析数据结果。

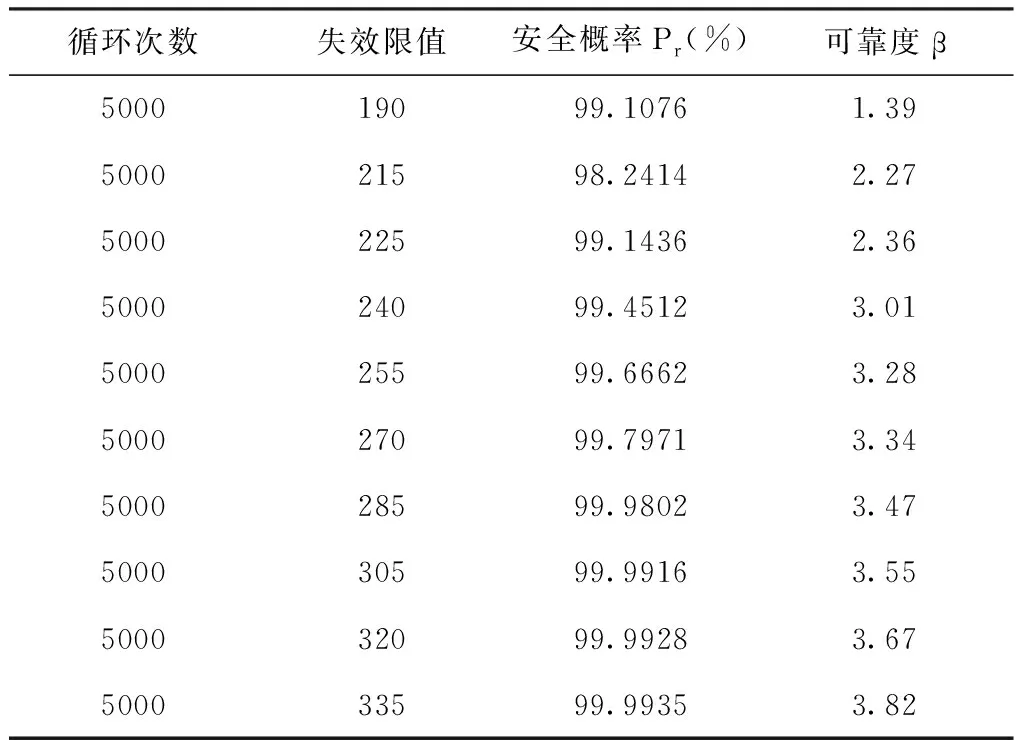
表2 相贯节点的可靠度分析结果

由表2可得，在多次循环测试下，该复杂建筑空间结构大直径相贯节点的失效应力值满足安全概率的弹性范畴。当大直径相贯节点的Pr值与β分别为99.9935%和3.82时，其失效应力限值是335MPa，比结构的设计屈服强度340MPa小，表明本文方法连接后的大直径相贯节点具备较高可靠性。

3.5 铸钢节点可靠度分析

为研究铸钢节点的失效应力值是否在安全概率的弹性范围内，现设置该复杂建筑空间结构的设计屈服强度为190MPa，表3为大直径相贯节点可靠性分析数据结果。

表3 铸钢节点的可靠度分析结果

由表3可得，在多次循环测试下，该复杂建筑空间结构铸钢节点的失效应力值仍然满足安全概率的弹性范畴。若Pr值与β分别为99.9994%和4.6，则对应的失效应力限值是79MPa，小于杂建筑空间结构的设计屈服强度190MPa，表明本文方法连接后的铸钢节点的可靠性高，安全性好。

3.6 延性分析

本节实验分析节点的变形能力，该变性能力可由位移延性系数来反映出来，该延性系数等于节点的极限与屈服位移的比。两种关键节点的荷载位移与位移延性系数结果如表4。

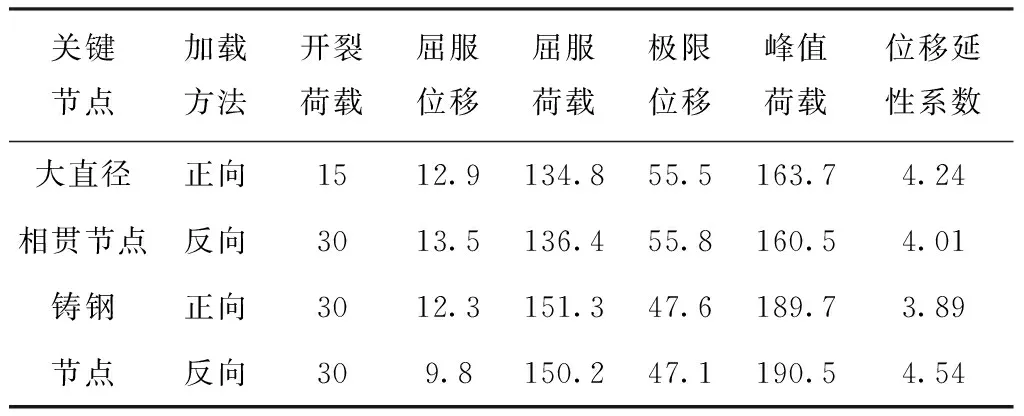
表4 关键节点荷载位移与位移延性系数

由表5可得，两种关键节点中，屈服位移值在9.8-13.5之间，极限位移值在47.1-55.8之间，通过计算可得，位移延性系数最大值与最小值分别为4.54与3.89，表明两种关键节点均具有良好的变形能力，符合结构的延性条件，表明本文方法连接后的节点具备较好的延性，可靠度较高。

3.7 承载力退化分析

基于固定的加载位移幅值，由于加载次数的增加，节点的承载力出现降低的情况，这种情况即为承载力退化。节点经过加载后，承载力逐步退化，退化后形成的规律可以用承载力退化系数表示，图5为两种关键节点在不同加载方式下的承载力退化曲线。

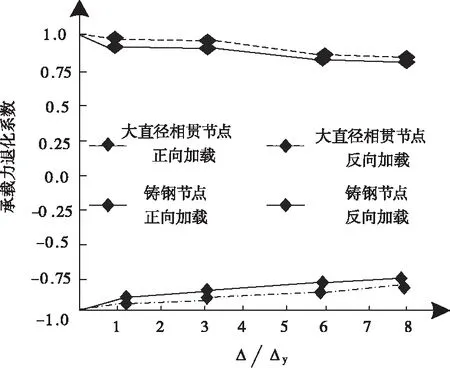
图5 承载力退化曲线

从图5中可看出，随着加载位移的增加，两种关键节点的承载力退化系数保持下降趋势，前期下降幅度较小，后其下降幅度增加，承载力退化加快，但承载力退化系数一直不低于0.75，实验表明，本文方法连接后的关键节点具有很强的承载力，退化速度缓慢。

4 结论

本文提出基于可靠度的复杂建筑空间结构节点连接方法，经实验验证，该方法连接后的复杂建筑空间结构的关键节点在轴线压力下具备较好的荷载位移曲线，同时两种关键节点在正方向加载方式下去屈服位移和极限位移均达到较好状态，且变形能力较强，具备较好的延性，且尽管随着加载位移的增加，承载力亦始终不低于0.75，表明本文方法连接后的节点具备较好承载力。本文方法可确保节点连接的可靠度高，抗震性强，极大限度的降低因地震等因素造成的生命财产的损失。