温室作物PSII光温耦合作用建模与仿真研究

高宏鼐，付丽疆，夏 倩，郭 亚

(江南大学物联网工程学院，江苏 无锡 214122)

1 引言

光合作用是所有生命活动的基础，由于耕地的减少和自然环境的不确定性增加，温室在现代农业中承载着重要的角色。目前智慧温室的环境参数调控策略往往脱离作物的光合生理需求，而作物的光合生理信息不仅包括植物表型信息，如植物叶片表面叶绿素荧光，光合作用机制分子层面的物质浓度的检测能够更加详细及准确地反映作物的光合生理，并且能够定量的表达作物环境条件对光合作用效率的影响，从而能够对作物光合作用进行更加合理精准的调控。目前农作物主要以C3植物为主，而C3植物光合作用机制的主要组成基本一致：包括捕光天线，光合中心等。叶片中有两个光系统，光系统I(PSI)和光系统II(PSII)。PSII对于外界环境因素的波动更加敏感，因此本研究仅考虑PSII活动[1]。PSII主要有两个组成部分：集光复合体和反应中心复合体。光系统中的吸光色素的功能类似于天线，将捕获的光能传输到叶绿素a的中心对，因此也称为集光复合体天线群。温度与光强是温室调控的两个重要环境参数。通常，当光照强度较强时，PSII天线分子会捕获更多的光能，因此会产生更多的受激分子参与光合作用的电子流；但是强光也会触发光合作用的光保护机制，以防止破坏叶片的内部结构；另外，温度的变化可改变PSII反应中心化学反应速率从而影响光合作用效率。

有关温室作物光合作用优化调控理论研究的相关工作起步相对较晚，目前光合作用调控的策略主要是根据相关实践经验或大量实验数据，胡瑾等人[2]基于实验数据统计学方法通过遗传算法研究了光环境目标值的寻优方法。朱周等人[3]依照经验响应模型获取光饱和点进行温室光环境调控。辛萍萍等人[4]通过实验数据先建立光照强度及CO2协同调控的次优目标值模型，再通过粒子群多目标寻优算法进行光合作用优化，或者将某些光合作用测量参数设为恒值进行调控，Iersel等人[5]将叶绿素荧光测量与发光二极管(LED)相结合，描述了如何通过调节LED的占空比来维持恒定的叶绿素荧光参数φPSII或ETR，但是可靠恒值往往是无法确定或者根据历史数据得到。而基于叶绿素荧光参数的光合作用优化研究，如贺通等人[6]基于相关叶绿素荧光参数，使用NSGA-II多目标优化算法得到在不同温度下的最优光强，从而增加生菜对光能的利用效率，无法直接建立叶绿素荧光参数与光合效率的关系。因此缺乏一种基于分子层面光合作用生理信息的有效优化调控策略。定量的优化调控通常需要一个能够反映植物生理的数学模型，而基于光合作用机制分子层面的建模方法相比植物表型信息的检测如叶绿素荧光来说能够更加方便地表达不同环境因子对光合作用效率的影响。因此一个能够反映C3植物PSII实时生理信息的数学模型的建立以及基于该模型的光温参数优化具有重要的理论意义和应用价值。

2 模型建立

温度会影响光合作用过程中的化学反应速度。如果需要使模型结构能够反映在不同温度下光合作用效率的不同，则温度应作为模型参数嵌入模型结构中。通常，化学反应速率常数在一定的范围内会随温度变化并满足Arrhenius公式，该公式已被广泛使用在各研究领域[7]。本文假设温室温度变化是在合理的范围内(根据农户或专家知识库可以确定)以保证不会因为过冷或过热损伤植物叶片，因此可以将Arrhenius公式应用于本研究建立的模型以满足温度对反应速率的影响。一类指数型Arrhenius公式可以表示为：

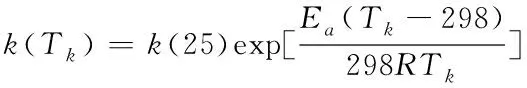
(1)

另一类Arrhenius公式是峰值函数，公式的变形描述了酶在较高温度下的构象变化给反应速率带来的影响。该式的等效形式可以表示为

(2)

温室植物叶片经过暗适应后，叶片上的天线分子(表示为A)在光照条件下可以捕获光能，随后变成激发分子(表示为A*)。被激发的分子上的能量有三个可能去向：通过叶绿素荧光耗散，以热的形式散失以及参与光化学反应以促进糖的产生和植物生长，在光子吸收过程中，由于不涉及化学反应，因此Arrhenius公式在该环节没有应用[2]。

当光照强度太高时，天线分子将携带大量光能进入光合作用系统，而高能量会破坏光合作用相关组织结构。在光合作用系统中，非光化学猝灭机制(NPQ)可以抑制高光能进入光合作用系统，NPQ主要组成部分之一是pH调节机制(qE)，它与叶黄素循环有关[9]，该叶黄素循环主要涉及两种物质：紫黄素(表示为N0)和玉米黄质(表示为N)。它们之间会相互转化，在管腔的H+梯度下，光强度越强，在腔内积累的H+越多(由于OEC中的水解作用)，导致N浓度的增加。N的主要作用是抑制外部多余光能进入光系统，从而使光能以热的形式损失。同样，指数型Arrhenius公式用来描述温度对该过程的影响。

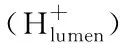
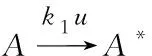
(3)

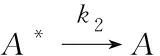
(4)

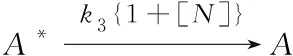
(5)

(6)

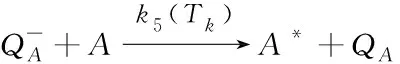
(7)

(8)

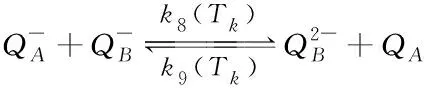
(9)

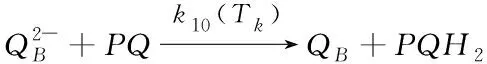
(10)

(11)

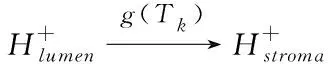
(12)

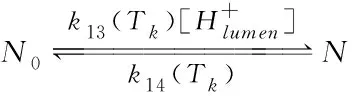
(13)

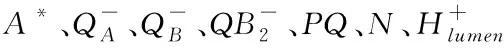
-k4(Tk)y1(1-y2)+k5(Tk)y2(290-y1)

(14)

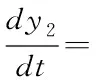
-k6(Tk)y2(1-y3-y4)+k7(Tk)y3(1-y2)

-k8(Tk)y2y3+k9(Tk)y4(1-y2)

(15)

-k8(Tk)y2y3+k9(Tk)y4(1-y2)

(16)

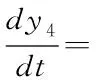
(17)

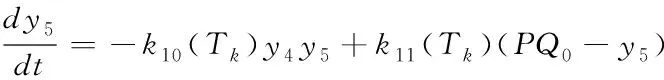
(18)

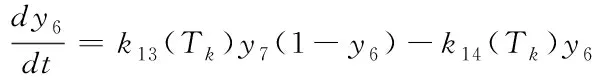
(19)

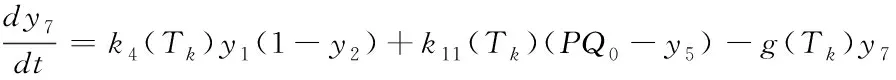
(20)

反应量v=k10(Tk)y4y5)与某一时刻PQ的还原效率有关，它可以反映用于正向光化学反应的光电子的量，其与最终的糖类生产及光合作用效率正相关[10]，因此这里用于衡量相对光合效率。研究在不同环境条件下相对光合效率对于将来在特定环境条件下光合作用的优化调控具有重要意义。

3 模型仿真与参数优化方法

3.1 模型仿真

为了进一步验证上述模型的有效性，本文通过列文伯格-马夸尔特非线性拟合方法(LM算法)[11-12]对模型仿真值与实验值进行对比，从而寻找使得仿真值与实验值误差最小的一组模型参数。具体的LM算法介绍如下：

目标：对于函数关系Y=f(b)，给定f(.)以及测量信号Y*，估计b。

Step1：取初始点b0，终止控制常数ε，k：=0，α0=10-3。

Step2：计算仿真值Yk=f(bk)，并计算误差函数ek=‖Y*-Yk‖。

Step 3：计算雅克比矩阵Jk，Jk的计算公式如式(21)所示，计算Nk=(Jk)T(Jk)+αkI，构造增量正规矩阵Nk*δk=(Jk)T*ek。

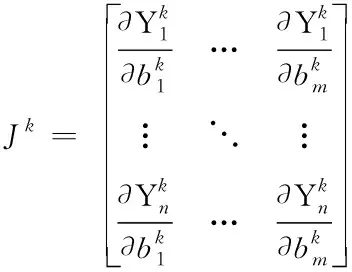
(21)

式(21)中m是参数b的维数，n表示输出的维数，Yn表示第n个仿真值。

Step4：求解增量正规方程得到δk

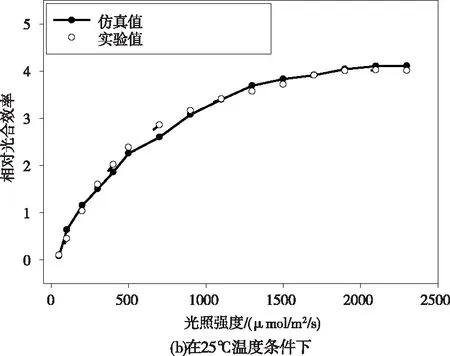
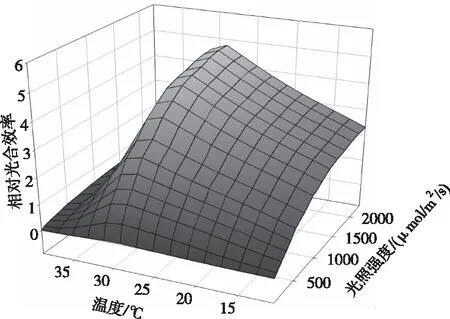
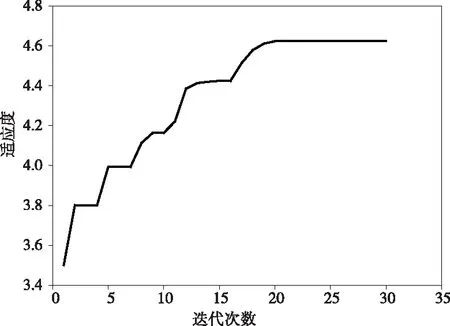
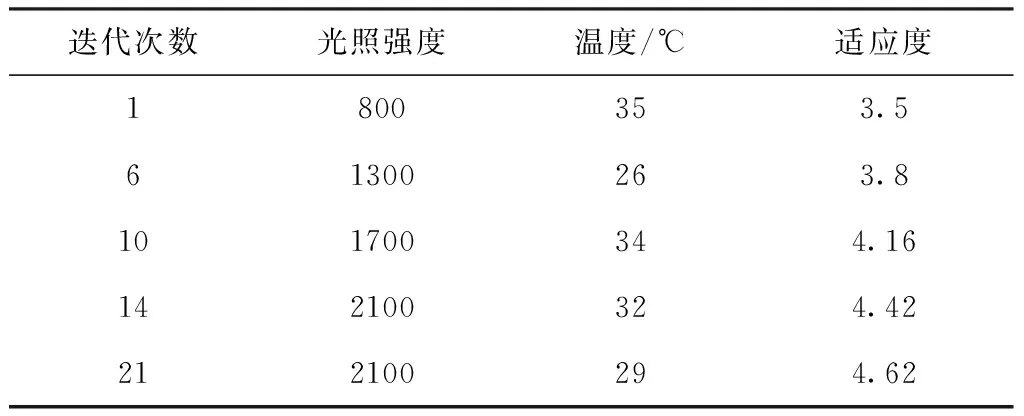
1)如果‖Y*-f(bk+δk)‖

2)如果‖Y*-f(bk+δk)‖≥ek，则令αk+1=2×αk，重新解正规方程得到δk，返回Step 1。

3.2 参数优化算法

在温室作物环境因素调控过程中，环境因素对植物光合作用影响的多样性使得基于光合作用实时信息的模型优化研究非常重要。本文通过粒子群算法对基于光合作用的PSII模型进行优化，寻找在该生长状态下最适宜的光温环境条件。粒子群算法(PSO)是从鸟类种群特性中得到启发并被人们广泛应用于解决各类优化问题的算法。在PSO算法中，用一种假定粒子来模拟上述所说的鸟类单个个体，每个粒子的当前所在位置就是所要求解决问题的一个候选解，粒子的移动前进过程就是该个体在这一区域的搜索过程。粒子的移动前进速度可以根据该粒子自身的历史最优位置以及该种群的历史最优位置进行不断的动态调整。通过不断更新粒子的速度及位置，最终可以得到满足优化问题终止条件的最优解[13-15]。近年来粒子群算法以其算法简单、收敛快、参数少等一系列优点被广泛应用于气温预测、机器人路径规划[16]以及组合优化等各个领域。PSO算法流程如下：

1)初始化。设置最大迭代次数，需要优化目标函数的自变量个数，设置粒子群规模，粒子的最大允许速度，位置为整个所需要搜索的空间，并在设定的速度区间以及空间上随机初始化各个粒子的移动速度和位置。

2)粒子个体极值及全局最优解。定义满足优化需求的适应度函数，个体极值为定义的每个粒子找到的自身最优解，进一步从这些粒子群自身最优解与自身的历史最优解进行比较，如果当前的适应度更佳，则将当前位置作为自身历史最佳位置。并进一步比较所有粒子的自身最优解，找到一个全局最优值作为本次全局最优解。并将本次全局最优解与历史全局最优进行比较更新。其中更新速度和位置的公式为

Vid=wVid+C1random(0，1)(Pid-Xid)

+C2random(0，1)(Pgd-Xid)

(22)

Xid=Xid+Vid

(23)

其中，下标i表示粒子群规模中的第i个，d表示适应度函数的自变量个数中的第d个；w为惯性因子，可以通过对w的变化来对全局及局部的寻优性能进行调整；C1和C2分别为个体及群体学习的加速因子；Pid表示第i个个体历史最优解的第d维；Pgd表示全局最优解的第d维。

3)终止条件。运行算法达到最大迭代次数或者代数之间的差值满足最小界限则停止算法，否则返回步骤2)。

4 结果

为验证所建立模型结构的有效性，通过LM算法拟合得到的模型仿真预测与文献[4]中番茄幼苗期叶子光合效率实验值曲线进行比较。作物实验条件分别在恒定光照强度(200 μmol/m2/s)不同温度条件下以及在恒定温度(25℃)不同光照强度两种不同实验状况下。实验数据与仿真数据之间的相对误差用于评估所提出模型结构的有效性。比较结果如图1所示。仿真值与实验值的相对误差为3.01%，3.7%。结果表明，本文所建立的模型结构可以有效地仿真在不同温度和光照强度下相对光合效率大小。

图1 相同光照条件下不同温度光合效率变化趋势图

图2 相同温度条件下不同光照强度光合效率变化趋势图

图3表示相对光合效率在光照强度及温度共同作用下的趋势图，从图中可以看出，随着温度的增强，相对光合效率会逐渐增加再逐渐减小；随着光照强度的增加，相对光合效率会逐渐趋于饱和。仿真结果能够明确仿真出在合适的环境条件下相对光合效率随着光照强度及温度的变化的趋势。

图3 相对光合效率在光照强度及温度共同作用下的变化图

在基于粒子群算法的相对光合效率优化研究中，设置种群大小为20，迭代次数为50次，惯性权重取0.8，两个学习因子分别都取1.5；粒子空间维数为两个即优化问题的自变量分别是光照强度和温度。光照强度及温度的范围都定义在正常的环境条件下，即光照强度取50-2300 μmol m-2s-1，温度取10-40 ℃。所建立模型中反应量v在模拟时间内稳定值设定为适应度函数。图3为算法迭代过程图，从图中可以看出，迭代次数基本在20次左右就达到最优，即粒子群算法能够快速收敛[23]并找到作物特定生长状况下最佳的光照强度与温度组合。表1列出了迭代过程中全局最优更新时的相关迭代次数及相应的环境条件和适应度，从表中可以看出植物在该特定生长状态下对应的最佳环境条件为2100 μmol photons m-2s-1，29℃。

图4 粒子群算法迭代过程图

基于粒子群算法对于光合作用活动的优化计算简单快捷准确，在将来的研究中，模型结构可能发生改变，更多的环境因子可纳入光合作用系统，此时粒子群算法快速全局搜索的优势将进一步凸显。本文仅通过基于两环境因子的光合作用PSII模型结构说明粒子群算法在光合作用优化中的有效性，为将来群优化算法更多地应用于光合作用模型优化提供依据，为进一步将更多的环境因素比如水分，无机元素等嵌入模型后的环境因素优化调控提供理论基础。

其迭代次数对应的环境条件见表1

表1 粒子群算法相关迭代次数及相应的环境条件和适应度

5 讨论

本文建立了仅包含7个状态变量的光反应PSII活动的模型，通过Arrhenius公式来描述温度对不同的光合作用反应的影响从而能够使模型仿真在不同的光照强度及温度下的光合作用效率。文献上，付丽疆等人[17]模拟了不同光照强度及温度对叶绿素荧光强度的影响，但是未考虑在较大的光照强度及温度范围内进行进一步优化研究，以及叶绿素荧光信号未能准确直观反映光合效率限制了其进一步的优化调控。Bernacchi等人从C3植物生化模型角度研究了温度对光合效率的影响，但是没有能够获取植物光合作用实时生理信息，也无法用于温室作物的实时优化调控。本文通过模型仿真值与实验值的对比说明该模型能够基于植物PSII分子层面实时生理信息模拟在作物正常生长的光照强度及温度范围内的相对光合效率，对于温室作物实际生产具有更好的意义。本文进一步基于建立的PSII活动数学模型，通过以相对光合效率为适应度，使用群智能优化算法中的粒子群算法对环境因子进行寻优，提供了获得基于植物生理需求的温室优化控制参数的方法思想，为将来进一步在更多环境因素耦合作用下最佳光合作用效率的搜索及调控提供了理论方法基础性框架。

光和温度是影响温室生产的两个重要环境因素，除了光照强度和温度以外，还有许多因素影响光合作用的效率，例如营养胁迫、盐胁迫、热胁迫、除草剂胁迫，这些因素都会导致光合效率的改变[18]。本文仅考虑了影响现代温室生产植物光合作用的两个主要可控环境变量光强度和温度。在未来的研究中，更多的不同环境条件可纳入本模型，以使其更全面仿真各种条件下的植物光合效率。作物生长优化调控的目的是增加农户的收益，如何进一步量化植物光合效率与作物产量之间的关系如植物汇源关系等将是未来研究的重点。

6 结论

在本研究中，建立含有7个状态变量的光合作用PSII简单模型结构，通过同Arrhenius公式定量描述不同温度对光合效率的影响。进一步通过非线性拟合方法分别拟合在不同温度以及不同光照强度下的相对光合效率，且误差很小(3%)。本文所建立的模型结构为将来研究不同环境因素对植物光合作用的耦合作用提供了建模框架，粒子群算法在优化光温耦合下相对光合效率中的应用表明了这一类群优化算法在温室作物光合作用环境调控及优化中的广阔前景。