基于网络演算的卫星网络端到端时延上界

魏德宾，王 旭，杨 力

(1. 大连大学通信与网络重点实验室，辽宁 大连 116622；2. 大连大学信息工程学院，辽宁 大连 116622；3. 南京理工大学自动化学院，江苏 南京 210094)

1 引言

近年来，卫星网络以其传输容量大、通信距离远、不受地形及自然灾害影响等特点得到广泛应用，成为地面通信的有益补充，也是实现全球无缝覆盖的重要手段。但是，卫星网络与地面网络相比带来了更大的时延，而网络的端到端时延作为网络服务质量(Quality of Service，QoS)最重要的参数之一，其边界分析的准确性直接影响到网络QoS的保障水平。

目前，网络的延时性能分析主要包括排队论和网络演算等方法。利用排队论方法对网络性能分析需要较精确的流量和服务模型，而对于当前日益复杂的网络形态和业务流特征，上述模型很难获得。网络演算[1]采用上界描述业务流的到达过程，采用下界描述服务过程，从而获得业务流的QoS性能界，使其分析方法更加灵活。文献[2]利用网络演算理论分析了无线多跳网络数据流端到端的服务曲线且利用服务曲线求解该网络的最大时延。周德新等人[3]利用网络演算求出了航空电子全双工交换以太网的时延上界。王子君等人[4]利用确定网络演算理论推导出了控制网络中的时延确定上界。文献[5]利用网络演算理论提出了基于分形漏桶的端到端时延上界模型。文献[6]利用确定性网络演算理论计算列车实时数据的端到端时延的上界。文献[7]利用网络演算对车联网中端到端的数据传输进行建模，计算其QoS参数，并基于建立的性能模型和遗传算法设计了车联网的QoS路由算法。HUANG J等人[8]针对SDN网络的QoS性能问题，提出一种混合调度模型，通过优先级队列和包通用处理器共享结合，利用网络演算进行建模来评估网络QoS性能。文献[9]利用网络演算对内容中心网络进行建模并分析其模型下LRU算法对数据流的影响。秦亮等人[10]针对远程测试通信网络实时性问题，建立了远程测试系统的网络演算模型，并利用网络演算理论推导了远程测试业务数据端到端延迟上界的数学计算方法。

上述文献，针对不同的地面网络环境通过传统网络演算推导时延上界，具有较好的表现。但是，在卫星网络中，由于其链路传播时延成周期性变化，且变化不能被忽略，传统网络分析方法[11-12]若是直接应用于卫星网络，将会导致对传播时延进行统一取值，不可避免的面临计算准确性的挑战。此外，为了得到端到端时延上界，传统时延边界计算过于放大排队时延，导致计算时延边界与实际时延相差较大，影响基于网络演算的QoS控制算法性能。因此，如何利用网络演算理论分析和精确求解卫星网络的端到端时延上界成了本文所关注的问题。

针对上述问题，本文基于网络演算提出了一种面向卫星网络的端到端网络模型与时延上界分析方法。首先根据卫星网络节点轨道参数、星下点位置等推导星间链路长度计算公式，通过星间链路长度推算链路的传播时延。其次，将链路处于峰值速率时的时延作为链路排队时延的上界，并结合链路传播时延与节点服务时延改进到达曲线。进一步，利用网络演算推导出卫星网络的端到端的时延上界。最后，分别研究网络端到端路径包含节点数目、节点服务速率、业务流权重值以及突发量等对卫星网络端到端时延上界的影响。

本文余下部分组织如下：第2节给出了本文用到的网络演算基本定义、推论；第3节给出卫星网络节点间传播时延计算公式；第4节给出了卫星网络端到端时延上界；第5节对第4节的结论进行数值计算与比较分析；第6节是结束语。

2 相关概念

2.1 网络演算理论

定义1(广义递增函数)：对于∀s≤t，若f(s)≤f(t)成立，则称f为广义递增函数。

定义2(广义递增函数集合)：若F={f(t)|f(t)=0，∀t<0，f(s)≤f(t)，t∈[0，+∞]}则称F为广义递增函数集合。

定义3(最小加卷积)：对于∀f，g∈F，函数f和g的最小加卷积运算为

定义4(到达曲线)：给定一个函数α(t)，且α∈F，t≥0，若输入流函数A满足A≤A⊗α，则称α是A的到达曲线。

定义5(服务曲线)：对于β∈F，β(0)=0，若满足输出流A*≥A⊗β，则称系统为数据流提供服务曲线β(t)。

推论1(水平偏差)：设一个流进入系统时被到达曲线α(t)约束，通过系统时系统提供服务曲线β(t)，则时延d(t)满足

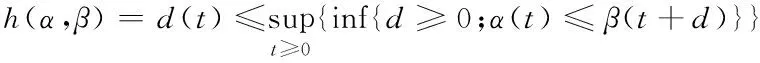
其中，h(α，β)也称作曲线α和β之间的水平偏差。

推论2(串联节点服务曲线)：系统1和系统2串联后提供的总服务曲线β为系统1提供的服务曲线β1和系统2提供的服务曲线β2的最小加卷积，即

β=β1⊗β2

3 星间链路传播时延分析

星间链路是卫星网络的重要组成部分，它可以在不依赖地面设备的情况下实现所有网络节点的连接，将卫星组合为一个整体。设Re为地球半径，hA，hB分别为卫星A与卫星B所在的轨道高度，(λ1，φ1)，(λ2，φ2)分别为卫星A与卫星B的星下点经纬度，它可由星历得到。则星间链路长度dBA可表示为

α=arccos[sin(φ1)sin(φ2)+cos(φ1)cos(φ2)cos(λ1-λ2)]

2颗卫星链路长度如图1。

图1 星间链路长度示意图

在实际情况中，由于星间链路会受到地球的遮挡，因此任意2颗处于不同轨道的卫星，它们之间的星间链路长度应存在一个最大值，即为最大可见链路长度，如图2。

图2 最大可见链路长度示意图

此时，卫星A与卫星B之间的链路长度dBA为其最大可见链路长度，可以表示为

由上述分析，可以得到两颗卫星星间链路长度计算公式，然后通过星间链路长度以及光速，得到节点之间的传播时延Dl为

其中，c为光速。

4 卫星网络端到端时延上界

卫星网络的端到端路径模型，如图3。

图3 端到端网络模型

卫星网络中节点1与节点m之间存在m-2个中间节点，当业务流A(t)到达节点时，会受到该节点参数为(r，b)的令牌桶限制，也即受该节点的到达曲线α(t)=rt+b的约束，b为突发通信量，r为数据流长期平均速率。

对于业务流A(t)，通过的每一个节点都会为业务流提供一定的服务能力。所以对任一网络节点，不管采用何种队列调度算法，都可以假定节点对数据流提供速率—延时服务曲线作为对数据流的服务保证。由此可得，路径中节点提供的服务曲线为：

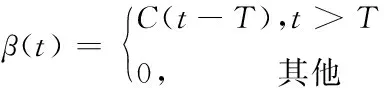
(1)

其中，C表示节点所提供的服务速率，T表示数据分组在节点的服务延迟。在这里，延迟参数可以认为是包处理时延，因此网络节点的延迟参数表示为

T=L/C

(2)

其中L表示最大包长。

又因为在卫星网络中，会存在多条业务流Ai(t)同时到达一个节点。假设业务流之间互相独立，且共享链路带宽W，为了业务流都可以得到相应的服务，在这里根据各业务流所分配的权重来进行带宽分配。若有n条业务流，假设业务流Ai(t)，i=1，2，…，n所分配的权重为ωi，则分配给业务流Ai(t)的服务速率Ci为

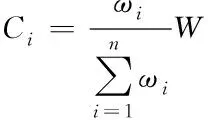
(3)

本文中使用上式中的Ci来代替式(1)中的C所得到的曲线为某个业务流Ai(t)的业务服务曲线。

在卫星网络中，端到端时延由节点处系统缓存的排队时延和链路传播时延以及节点间的发送时延3部分组成。

定理1(单节点时延上界)：假设一个业务流Ai(t)通过节点p，该节点的到达曲线为α，服务曲线为β，则该业务流通过该节点的延时Dp为

(4)

其中，Wt为上一节点到目前节点的链路的峰值速率。Ti表示业务流Ai(t)在节点p处的服务延迟。

定理2(端到端时延上界)：假设一个业务流Ai(t)依次通过m个节点，节点中的到达曲线依次为αi，i=1，2，…，m，系统的服务曲线依次为βi，i=1，2，…，m，相邻2个节点之间的传播时延依次为Dl1，Dl2，…，Dlm-1，中间节点的发送时延依次为：Df1，Df2，…，Dfm-1，则端到端时延上界D1→m为

(5)

证明：用数学归纳法证明。

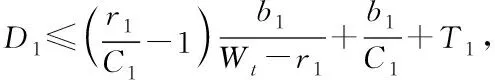
所以第1、2两个节点之间的端到端时延为

D1→2=D1+Dl1+Df1+D2

由此可见，式(5)成立。

2)假设当m=k-1时，定理2成立，即

由定理1可以得出，第k个节点的时延为

显然，节点1到节点k的端到端时延D1→k等于其前k-1个节点的时延D1→k-1和第k个节点的时延Dk之和，即

D1→k=D1→k-1+Dk

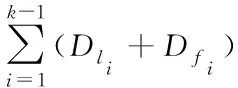
5 仿真验证

5.1 仿真设置

本文仿真以铱星星座为网络模型进行仿真和数值计算。具体星座参数见表1。

表1 铱星星座参数

其中，卫星间的ISL(Inter Satellite Link)链路带宽是500Mb/s，数据流长期平均速率为80Mb/s，数据流的突发量为200kbits，系统的服务速率为100Mb/s，两相邻节点的发送时延设定为0.2ms，包的平均大小为1000bits。根据所设定的参数以及铱星星座拓扑如(图4所示)，分别研究端到端路径所含节点数目、节点服务速率、业务流权重值以及突发量等对卫星网络端到端时延上界的影响。

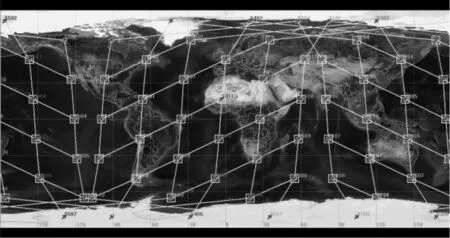
图4 铱星星座拓扑图

5.2 实验结果分析

将本文提出的卫星网络的端到端时延上界与基于令牌桶的端到端理论时延上界以及MATLAB仿真得到的铱星星座端到端时延上界进行比较，结果如图5所示。

图5 端到端时延与路径节点数

从图5可以看出，当卫星网络端到端节点数目增加时，理论时延与仿真时延都增大，且基于令牌桶的端到端时延要较本文所提方法的理论值偏高。这是因为：第一，本文基于卫星网络的端到端时延上界分析方法，考虑了卫星网络节点随时间变化，其传播时延也随之变化的特点。第二，将链路处于峰值速率时的时延作为链路排队时延的上界，计算得到卫星网络端到端时延上界更加准确。此外，随着路径中节点数目的增加，仿真得到的时延与本文所提方法的理论时延上界越来越接近，此结果反映了当链路上的节点数多时，网络演算能反映真实的网络时延性能。

在图6中，设定端到端路径中的节点数为7。从图中可以看出，当服务速率值较小时，仿真值与理论的时延差距较大，这是因为链路负载过重，造成网络拥塞，从而导致仿真值与理论计算的时延差距较大，随着服务速率的增大，网络状况转好，仿真值与理论时延差距逐渐减小，尤其是在服务速率达到400Mb/s之后，仿真值与理论时延差距较小，更加接近本文所提方法求得的理论值。

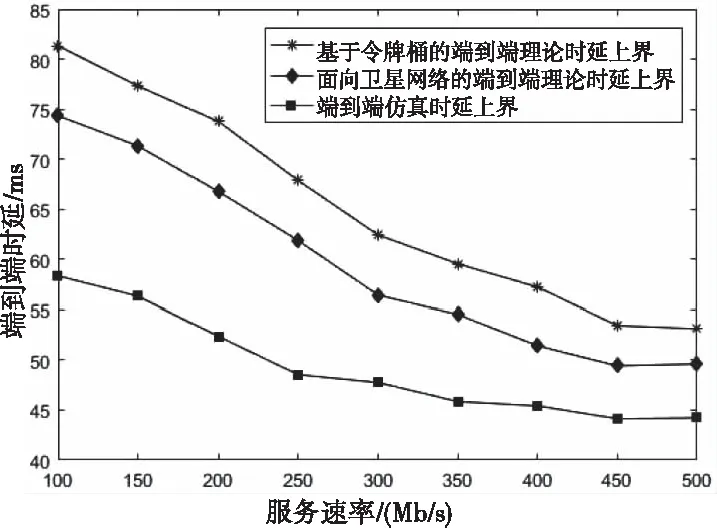
图6 端到端时延与服务速率

当端到端路径中的节点数为7时，从图7可以看出，理论时延与仿真时延都随着业务权重值的增大而减小，且这种减小的趋势变得越来越平坦。这是因为随着业务权重值的增大，节点的服务速率也随之增大，导致时延随业务权重值的增大而减小。但是在权重值小于0.5时，时延下降较快，而权重值大于0.5之后，趋于平坦。这是因为随着节点的服务，网络趋于稳定，使得相应的数据流都得到了相应服务，从而导致时延趋于平缓。网络端到端时延仿真值与本文所提出方法求得的时延理论值上界越来越接近，从而验证了基于网络演算推导得出的卫星网络时延上界能更好的反映地卫星网络性能。

图7 端到端时延与权重

当端到端路径中的节点数为7时，从图8中可以看出，随着突发量的增加，端到端仿真时延值也随之增大。而在仿真初期，端到端仿真时延值增长速度过快，而在达到一定突发量值时，端到端时延趋于平缓并接近理论值。这是因为在仿真初期，网络并不稳定，而此时突发量在增加，导致时延增长速度较快，而在网络处于相对稳定之后，随着突发量的增加，且节点间具有负载均衡能力，使得时延增长缓慢。

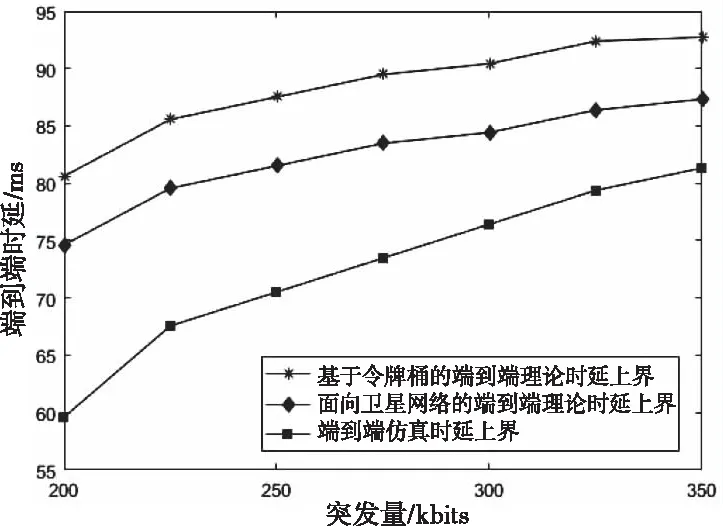
图8 端到端时延与突发量

当端到端路径中的节点数为7时，从图9中可以看出，随着链路带宽的增加，端到端仿真时延值也随之增大。而在仿真初期，端到端仿真时延值增长速度过快，而在达到一定链路带宽值时，端到端时延趋于平缓并接近理论值。这是因为在仿真初期，网络并不稳定，节点服务速率小于链路带宽，导致时延增长速度较快，而在网络处于相对稳定之后，随着链路带宽的增加，且节点间具有负载均衡能力，使得时延增长缓慢。

图9 端到端时延与链路带宽

当端到端路径中的节点数为7时，从图10中可以看出，随着两节点间的发送时延的增加，端到端仿真时延值也随之增大，且越来越接近于本文所提方法求得的理论值。这是因为，两节点间的发送时延的增加，导致节点转发效率降低，使得时延增长较快，但是在网络处于相对稳定之后，随着发送时延的增加，且节点间具有负载均衡能力，使得时延增长缓慢，更加接近本文所提方法求得的理论值。

图10 端到端时延与发送时延

6 结论

本文提出的卫星网络的端到端时延分析方法，通过计算星间距离得到传播时延，以及设置节点的到达曲线与服务曲线并结合卫星网络模型，推导出了卫星网络的端到端的时延上界。仿真结果表明，本文方法得到的卫星网络端到端时延上界比传统方法更接近于仿真值，能够为网络QoS控制提供支持。