基于主成分回归的运输飞机超轮速诱因研究

钱 宇，龙 涛

(中国民用航空飞行学院，四川 广汉 618307)

1 引言

民航运输飞机起飞离地速度是飞机主轮离地时的瞬时速度，该速度超过轮胎型号限制速度，即发生超轮速[1]。由于超轮速极易造成轮胎超负荷损伤，甚至爆胎，严重威胁航空安全运行[2]，因此对超轮速的研究尤为重要。飞机起飞离地速度受多种因素的影响，目前对超轮速诱因的研究多为定性分析[3][4]。快速存取记录器(Quick Access Recorder，QAR)用于日常运行时获取飞行数据，飞行数据能够反映飞机运行情况。因此，为客观分析超轮速诱因，进行识别风险，可以使用QAR数据对超轮速诱因进行定量研究。

超轮速诱因研究涉及多个变量，且变量间相关性明显。为使研究问题得到简化，降低建立模型的难度和复杂性，并保证模型的合理性，需要对多个变量进行降维，而主成分分析是一种常用的降维方法。Chuanqi Lu等[5]利用主成分分析法对航空液压泵的故障特征进行降维，建立支持向量回归模型对故障规模进行识别；刘科生和王思洋[6]对函数型自变量进行主成分提取，降低参数估计的复杂性；李鼎哲等[7]利用主成分分析法将航空发动机工作状态数据进行属性约简，输出作为随机森林原始训练集；Shane Kosir等[8]利用主成分分析法处理航空燃油容积膨胀数据，所得主成分用于训练神经网络。

研究以民航客机起飞离地速度为对象，依据QAR所记录的发生超轮速事件的飞行数据，利用主成分分析方法对影响起飞离地速度的多个参数进行降维，建立主成分回归模型，得出各参数与离地速度的定量关系。

2 QAR数据及参数选取

QAR数据涵盖了飞行过程中上千个不同的参数，如经纬度、高度、风向风速、温度、速度、侧杆输入等。因此，飞行数据分析和应用一直是航空安全研究的热点之一。目前对QAR数据的应用研究在飞机性能分析[9]和故障诊断[10]、飞行员操作特征研究[11]、风险评估和预警[12]等方面发挥着巨大的作用。

研究选取影响起飞离地速度的26个参数，基于QAR数据建立超轮速诱因分析模型。所选参数分为机组操纵类、飞机性能类、飞机姿态类、飞机位置类和环境类等5类，具体分类情况见表1。

表1 起飞离地速度影响参数分类情况

3 诱因分析模型

3.1 主成分分析

采用主成分分析(Principal Component Analysis，PCA)方法，将多个变量化为少数几个主成分(综合变量)，实现降维。这些主成分可以表示为原始变量的线性组合，能够反映原始变量的大部分信息，且各主成分之间互不相关[13]。主成分分析模型的建立过程如下：

1)原始数据标准化处理

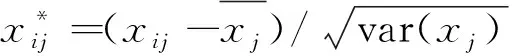
(1)

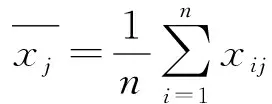
(2)

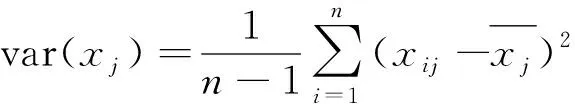
(3)

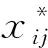
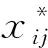
R=(rij)p×p

(4)

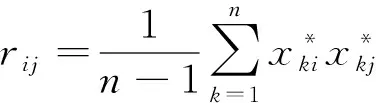
(5)

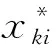
3)求解R的特征值λ和正交单位特征向量e

由特征方程|R-λD|=0，计算得出R的特征值λ和特征向量D，将特征值由大到小进行排序，得到λ1≥λ2≥…≥λp；利用施密特正交化方法将特征向量D正交规范化，再对向量进行单位化处理，得到正交单位特征向量e，即主成分表达式的系数。

4)计算贡献率ci和累积贡献率C

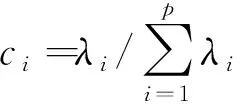
(6)

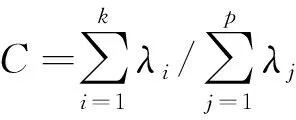
(7)

式中，λi、λj分别为R的第i和第j个特征值。

5)计算主成分得分score。

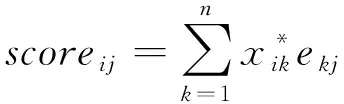
(8)

式中，i，j=1，2，…，p，ej为相应主成分表达式的系数，scorej表示第j个主成分得分，主成分得分可用于进一步的统计分析。

3.2 主成分回归模型

通过主成分分析方法得到主成分得分和主成分表达式。将各主成分得分作为回归模型的输入，得到主成分回归方程，使原始回归模型得到简化，并使得回归方程和参数估计更加可靠；将主成分表达式代回回归模型，即可得到因变量关于标准化自变量的回归模型。模型建立过程如下：

1)变量共线性诊断与相关性分析

VIF=1/(1-R2)

(9)

式中，VIF为方差膨胀因子；R2为判定系数，R2=1-SSE/SST，SSE为误差平方和，SST为变量的总离差平方和。VIF越大说明变量间共线性越严重，一般，VIF<5，认为不存在共线性；VIF>10，认为共线性严重。

2)建立多元线性回归模型

采用普通最小二乘法，建立因变量y关于主成分Z1，Z2，…，Zk的回归模型

y=β0+β1Z1+β2Z2+…+βkZk+ε

(10)

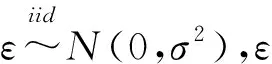
3)显著性检验

给定显著性水平α=0.05，对回归方程进行显著性检验(F检验)，若F检验的p值小于0.05，则应拒绝原假设H0：β1=β2=…=βk=0，可认为回归方程是显著的。然后，对方程的常数项和线性项进行显著性检验(t检验)，若t检验的p值小于0.05，则说明方程各项系数是显著的。

4)残差分析和异常值诊断

通过残差直方图和残差正态概率图检验残差是否服从正态分布，然后通过学生化残差统计量Se查找异常值。去除异常值并剔除不显著的线性项，重新建立回归模型。

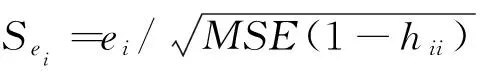
(11)

式中，ei为第i个观测对应的残差，MSE为均方残差，hii为帽子矩阵H=X(XTX)-1XT对角线上的第i个元素。

5)回代主成分表达式

(12)

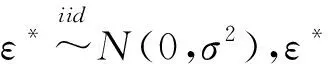
建立主成分回归模型的流程图如图1。

图1 主成分回归模型建立流程图

4 算例分析

4.1 样本总体分析

研究选取144组航班QAR数据作为样本。为判断样本是否适合进行主成分分析，通过Kaiser-Meyer-Olkin (KMO)检验和Bartlett’s test of sphericity(Bartlett’s)检验对数据进行总体分析[14]。一般，KMO检验值分布在0～1之间，若系数值大于0.6，则认为样本的数据结构合理且满足要求；Bartlett’s检验基于各参数互不相关的假设，即各参数无法进行降维。因此，若Bartlett’s检验的p值小于0.001，则拒绝原假设，说明样本可以进行主成分提取。检验结果见表2。

表2 样本总体分析检验结果

从表2的检验结果可以看出，样本数据可用于主成分分析。

4.2 主成分分析

考虑各参数的量纲不同，故将原始数据进行标准化处理，对标准化数据进行主成分分析的结果如图2和表3。

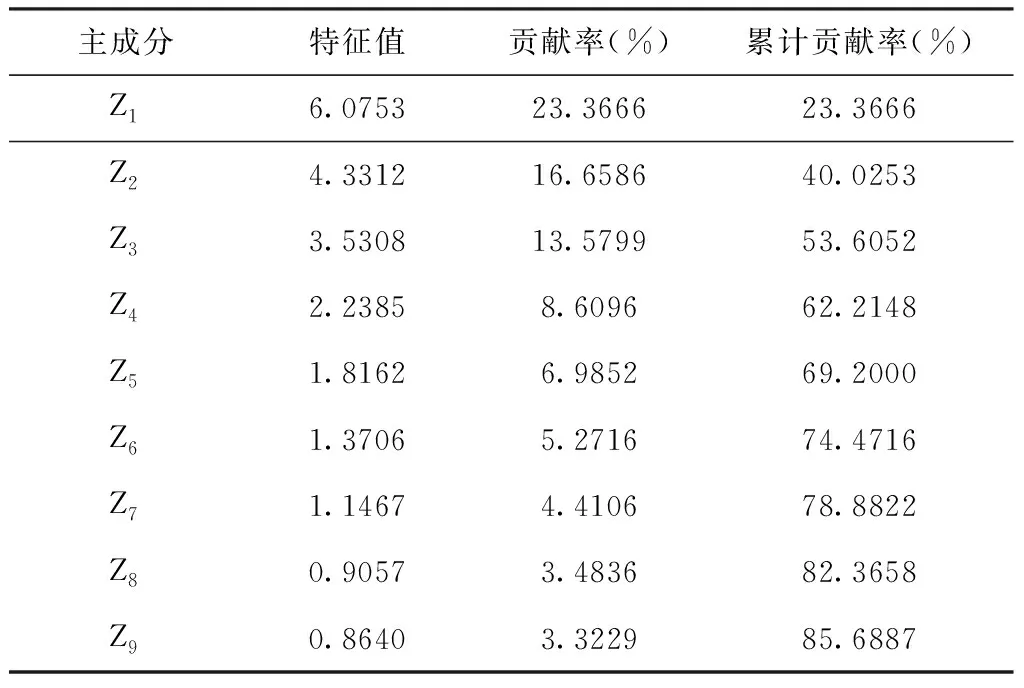
表3 主成分分析结果

由于前9个主成分的累积贡献率已经达到85.69%，超过85%，且综合考虑累积贡献率和各主成分的特征值(方差)，前9个主成分已经具有足够的解释能力，故确定选取前9个主成分作为回归模型的自变量。

图2 主成分贡献率和累计贡献率图

所选主成分关于原始变量的表达式系数见表4。其中，Zi表示各主成分，Xi表示标准化的原始自变量，i=1，2，…，26。

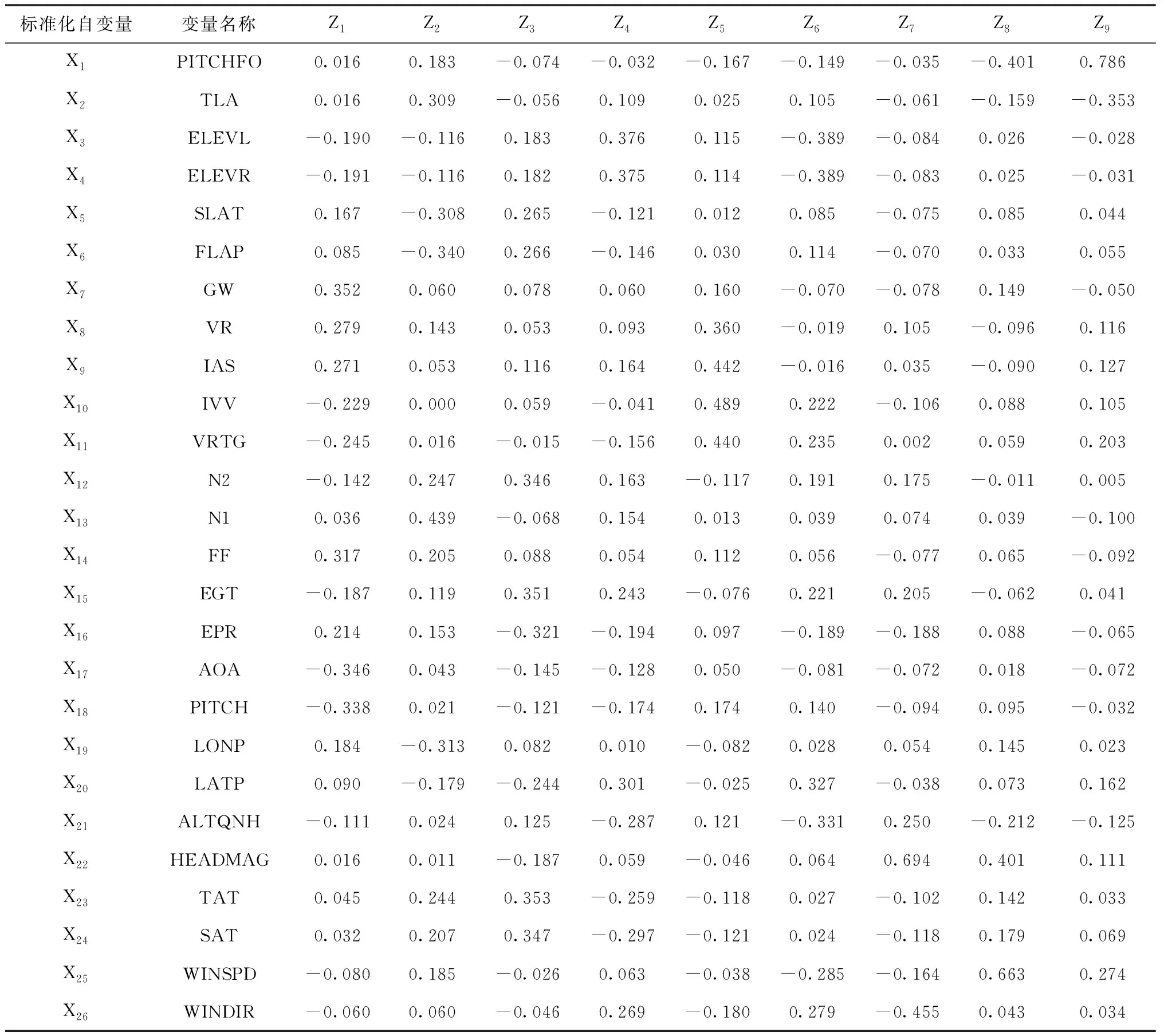
表4 所选主成分关于原始变量的表达式系数

4.3 主成分回归分析

经多重共线性诊断，各主成分的方差膨胀因子VIF计算结果均为1，说明各主成分间不存在共线性。然后以主成分Z1，Z2，…，Z9为自变量，以离地速度y为因变量，通过相关性分析，得到各变量相关系数如图3。

图3 离地速度与各主成分的相关系数矩阵图

从图3可以看出，各自变量与因变量之间均存在相关性。

建立初始线性回归模型，得到回归分析结果见表5。

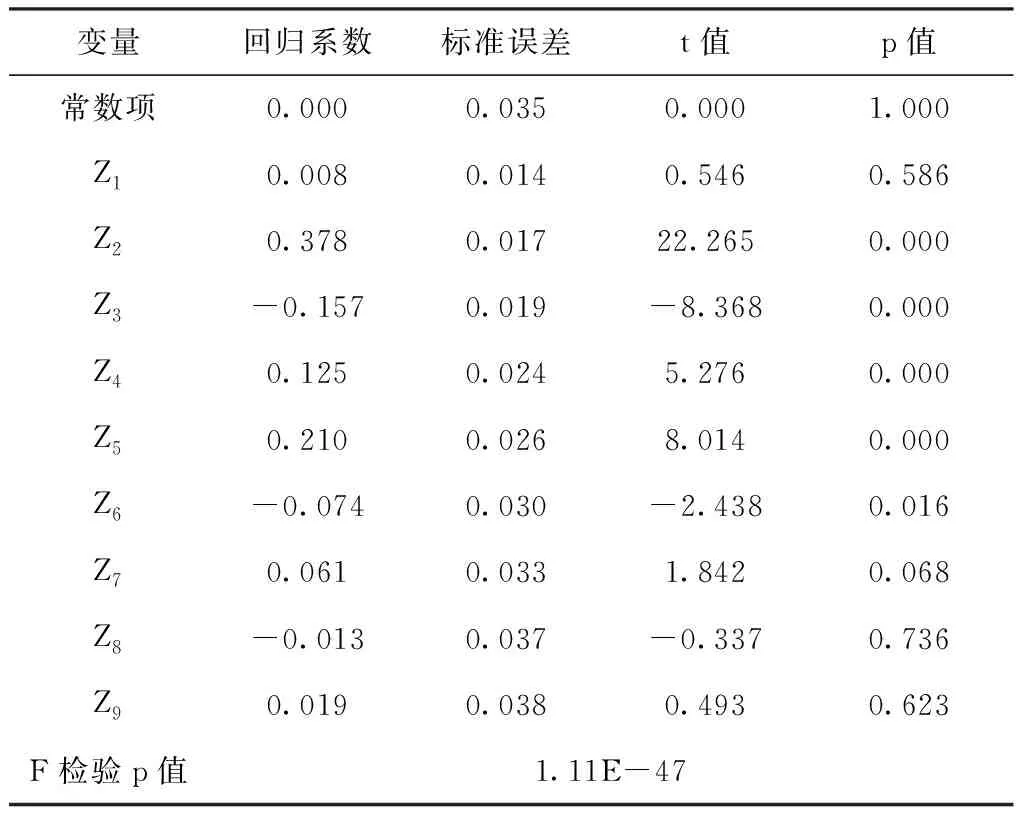
表5 初始线性回归模型参数估计结果

由表5得到初始线性回归方程：

y=0.008Z1+0.378Z2-0.157Z3+0.125Z4+0.210Z5-0.074Z6+0.061Z7-0.013Z8+0.019Z9

回归方程的F检验p值小于0.05，说明该方程通过显著性检验，整体显著；从表中常数项和各线性项t检验的p值可以看出，回归系数中的常数项和线性项Z1、Z7、Z8、Z9所对应的p值均大于0.05，说明其均不显著。

对回归模型进行残差分析和异常值诊断，所得结果如图4和图5。

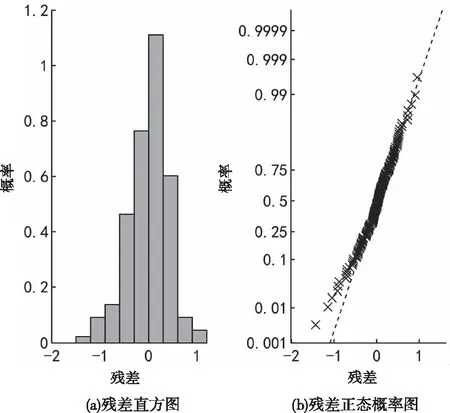
图4 初始线性回归模型残差分析结果

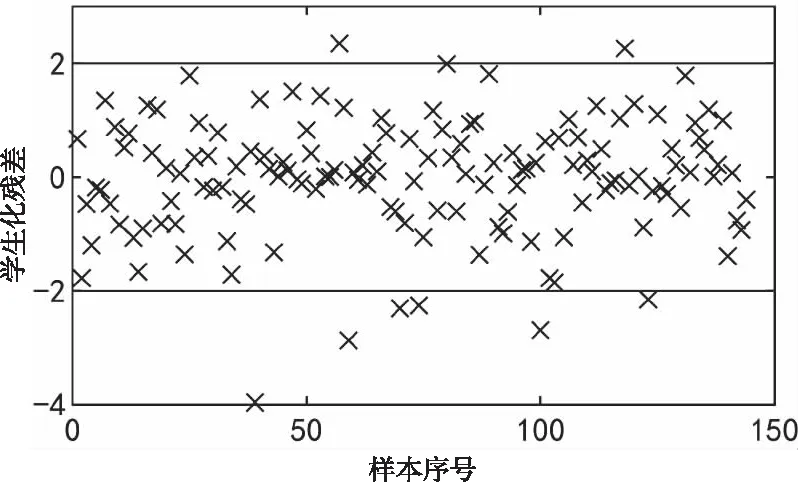
图5 初始线性回归模型异常值诊断结果

从残差直方图中可以看出，残差基本呈正态分布；残差正态概率图的下尾部分偏离直线，说明存在异常值。根据学生化残差查找异常值，得到8组存在异常的样本。去除异常值并剔除不显著的线性项，重新建立线性回归模型，参数估计结果见表6。

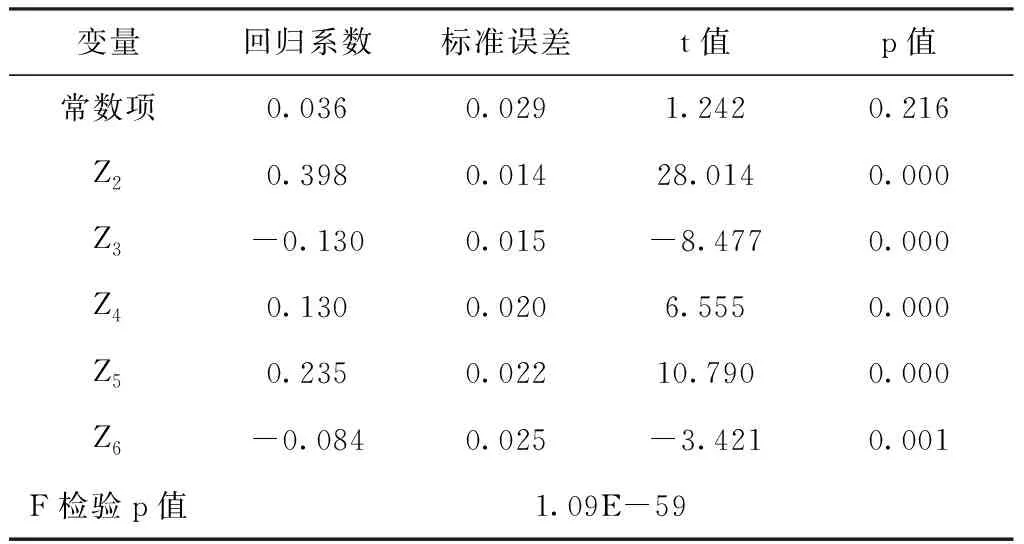
表6 去异线性回归模型参数估计结果

由表6得到去异线性回归方程为：

y=0.398Z2-0.130Z3+0.130Z4+0.235Z5-0.084Z6

对回归方程的显著性检验p值小于0.05，说明方程整体是显著的。除了常数项外，各线性项的t检验p值均小于0.05，说明各线性项均显著。

表7 回归模型拟合效果评价结果对比

参数的置信区间能够反映参数真实值在某个可信程度下处于某区间。计算去异线性回归模型中回归系数在95%可信程度下的置信区间，结果见表8。

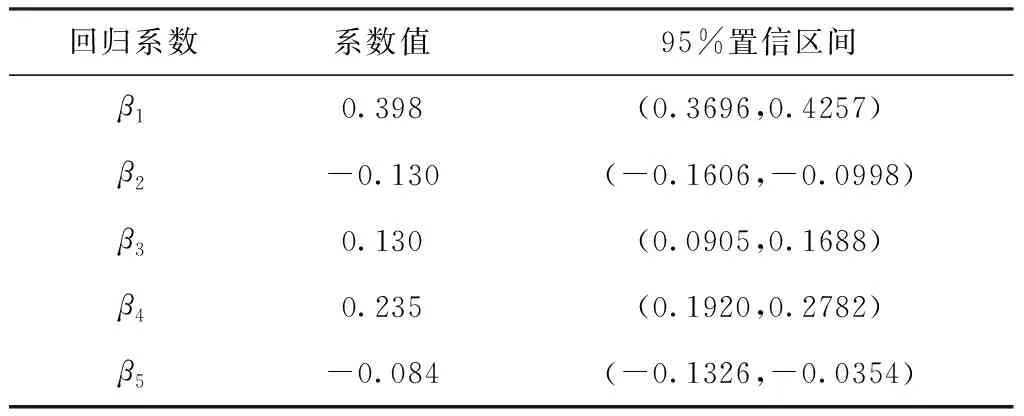
表8 去异线性回归模型回归系数置信区间

表8反映了在95%置信水平下，去异线性回归模型的各回归系数分别处于表中所示相应区间内。

将主成分与标准化原始变量的表达式系数代入去异线性回归方程，得到用标准化自变量表示的回归方程：

y=-0.191X6-0.177X5+0.141X2+0.052X1+0.039X3+0.038X4+0.203X13+0.148X8+0.132X9+0.116X16+0.099X14+0.083X10+0.072X11+0.065X7+0.031X12-0.003X15+0.038X17+0.031X18-0.155X19-0.034X20+0.012X21+0.020X22+0.100X25-0.032X24-0.013X23-0.001X26

4.4 诱因分析

观察以标准化自变量表示的回归方程和表1中的参数分类情况，可以发现：

1)变量X6(襟翼角度)、X5(缝翼角度)、X15(发动机排气温度)、X19(经度)、X20(纬度)、X23(总温)、X24(静温)和X26(风向)的系数为负，其余均为正。方程系数为负，说明起飞离地速度随相关变量减小而增大；反之，方程系数为正，起飞离地速度随相关变量增大而增大。

2)对起飞离地速度影响较大的因素分别是低压转子转速、襟翼角度、缝翼角度、经度。表现为低压转子转速越高，越易超轮速；起飞襟翼和缝翼伸出角度越小，越易超轮速；起飞位置越靠近我国西部，即经度越小，越易超轮速。此外，影响其次的是油门、抬前轮速度、指示空速、发动机压力比、风速等；影响最小的两个因素分别是发动机排气温度和风向。

3)尽管风向的回归系数值仅为0.001，但这并非说明风向对起飞离地速度几乎没有影响。经分析，由于风向和风速构成一个矢量，当顺风风速越大，起飞离地速度越大，越容易超轮速，符合实际情况。

5 结论

利用发生超轮速事件的航班QAR数据，通过主成分回归分析方法，所建立的包含机组操纵、飞机性能、飞机姿态、飞机位置和运行环境等参数的运输飞机超轮速诱因分析模型，实现了各参数与起飞离地速度的定量关系估计，解释了起飞离地速度的影响因素及其影响程度，为飞行训练及起飞风险预测奠定了基础。