理清数学思想方法，巧学“代数式”

文／毛倩倩

一、整体思想

整体思想指的是对于一个数学问题，着眼于问题的整体结构，从宏观上理解和认识问题；通过全面地观察和思考，挖掘已有元素在整体结构中的地位与作用，从而找到解决问题的办法。

例1已知a2-2a=1，求2-3a2+6a的值。

【解析】若先求出字母a的值，再代入求值，比较复杂，我们以现有的知识也不具备应用这种解法的能力。若能从全局出发，考虑条件与结论的整体配合，不难发现，代数式a2-2a与-3a2+6a存在倍数关系。

解：由乘法分配律，

得2-3a2+6a=2-3·（a2-2a）。

将a2-2a=1代入，得

2-3a2+6a=2-3×1=-1。

例2已知a2-ab=4，ab-b2=-3，求a2-b2和a2-2ab+b2的值。

【解析】从整体结构考虑，将a2-ab、abb2相加，可以抵消ab，得到代数式a2-b2；将两个代数式整体相减，则可得到代数式a2-2ab+b2。

解：因为a2-b2=a2-ab+ab-b2=（a2-ab）+（ab-b2），所以将a2-ab=4，ab-b2=-3代入，得a2-b2=（a2-ab）+（ab-b2）=4+（-3）=1。

因为a2-2ab+b2=a2-ab-ab+b2=（a2-ab）-（ab-b2），所以将a2-ab=4，ab-b2=-3代入，得a2-2ab+b2=（a2-ab）-（ab-b2）=4-（-3）=7。

二、数形结合

数学是一门研究数量关系和空间形式的科学，数形结合就是将抽象的数学语言与直观的图形结合起来，将数与形两种信息按解决策略的需要进行转换，发挥各自的优势。

例3有理数a、b、c在数轴上的位置如图1所示，请化简|a-b|+|c-a|-|b-c|。

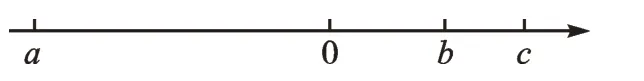
图1

例4如图2，数轴上4个点表示的数分别为a、b、c、d。若 |a-c|=9，|a-d|=11，|b-d|=7，则 |b-c|的值为________。

图2

【解析】根据a、b、c在数轴上的位置，判断它们的大小关系，从而去绝对值化简。

解：根据数轴可得a＜0＜b＜c，

所以a-b＜0，c-a＞0，b-c＜0。

所以|a-b|+|c-a|-|b-c|

=b-a+c-a-（c-b）

=b-a+c-a-c+b=2b-2a。

【解析】结合数轴，将条件与结论中出现的“两个数的差的绝对值”赋予几何意义，将其看作两点之间的距离，即线段的长度，由线段的数量关系可解决问题。

解：由图可知，|a -c|=9指的是表示a的点与表示c的点之间的距离是9，|a -d|=11指的是表示a的点与表示d的点之间的距离是11，所以，表示c的点与表示d的点之间的距离是 |c-d|=2。又因为 |b-d|=7指的是表示b的点与表示d的点之间的距离是7，所以，表示b的点与表示c的点之间的距离是 | b-c|=5。

三、分类讨论

我们研究的问题有时包含很多种可能，不能一概而论。有的是问题的结论不是唯一确定的，有的是在解题中一些算式不能以统一的形式出现，还有的是字母的取值会影响结果等，这就需要根据问题的特点和要求，将问题分成若干类，转化为若干个小问题来解决。

例5已知a、b是有理数，试比较代数式a+b与a-b的大小。

【解析】这里a、b的取值会影响两个代数式的大小比较，所以需要进行分类讨论。观察两个代数式，发现都有相同的部分“a”，比较a+b与a-b的大小，就是比较b与-b的大小。

解：根据“作差法”可得，（a+b）-（a-b）=a+b-a+b=2b。

当b＞0时，2b＞0，则a+b＞a-b；

当b=0时，2b=0，则a+b=a-b；

当b＜0时，2b＜0，则a+b＜a-b。

例6（1）尝试：比较下列各式的大小关系。（用“＞”“＜”“=”“≥”或“≤”填空）。

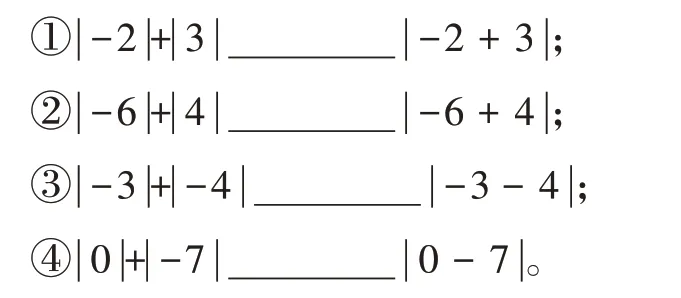
（2）归纳：观察上面的数量关系，可以得到：|a|+|b |________|a+b（|填“＞”“＜”“=”“≥”或“≤”）。

（3）应用：利用上面得到的结论解决问题：若|m|+|n|=10，|m+n|=4，则m=______。

（4）拓展：当|a|+|b|+|c|＞| a+b+c|成立时，a、b、c应满足的条件是________。

①1个正数，2个负数；②2个正数，1个负数；③3个正数；④3个负数；⑤1个0，2个正数；⑥1个0，2个负数；⑦1个0，1个正数，1个负数。

【解析】问题（1）可以通过计算做出判断，①②③④分别填＞、＞、=、=。问题（2）可依据（1）中列举的具体例子，通过不完全归纳，发现规律|a|+|b|≥| a+b（|a、b同号或至少一个为0时取等号）。问题（3）可根据问题（2）中的结论予以解决，由|m|+|n|＞| m+n|可知m、n异号，接下来进行分类讨论：当m＞0，n＜0时，m=3或7；当m＜0，n＞0时，m=-3或-7。问题（4）是问题（2）的拓展，由|a|+|b|+|c|＞| a+b+c|可知a、b、c的符号需要分为多种情况讨论，①②⑦都满足。