加劲式压力钢管临界外压数值计算方法

苏 凯，王博士，朱洪泽，陶 军，徐振东

(1.武汉大学 水资源与水电工程科学国家重点实验室，湖北 武汉 430072；2.武汉大学 水工岩石力学教育部重点实验室, 湖北 武汉 430072；3.海绵城市建设水系统科学 湖北省重点实验室（武汉大学），湖北 武汉 430072)

压力钢管作为一种超薄壳圆柱结构，由于其布置灵活、节省钢材、运行可靠等优点，在大中型水电站、水资源配置工程中有着悠久的应用历史[1–2]，但在外水压力或施工期间灌浆压力的作用下，钢管放空时很可能发生屈曲失稳破坏，不仅给工程带来巨大经济损失，而且往往难以修复。

对于压力钢管这种圆柱薄壳结构，相关学者在临界外压作用下屈曲失稳方面进行了大量研究。马文亮等[3]考虑了初始缺陷因素，采用解析法和半解析有限元法分别对埋藏式加劲压力钢管进行外压稳定性计算；梁月英[4]、李明[5]等在屈曲和稳定性理论的基础上，利用线性和非线性有限元法分析外压作用下压力钢管的前屈曲和后屈曲临界失稳荷载；Showkati等[6]基于静水压力下加劲式管道屈曲试验，分析了加劲式管道的初始屈曲模式、屈曲扩展模式、后屈曲模式、屈服线的发展模式及管道的最终破坏模式；董文胜[7]和Dong[8]等提出一种将遗传算法与神经网络结合对柱壳结构最小临界失稳荷载进行仿真求解的计算方法；de Paor[9]、宋广凯[10]、王黎辉[11]等基于非线性屈曲数值仿真计算方法，研究了柱壳结构在受到侧压、轴压载荷复杂作用下的非线性屈曲行为；慕园等[12]基于结构屈曲理论，考虑加劲环和管壁的相互作用，分析了钢管的线性屈曲情况；伍鹤皋[13]、鲁志航[14]、齐文彪[15]等对国内外压力钢管屈曲外压计算常用的Mises精确式和相关规范采用的近似式等方法进行了比较研究，并结合工程案例对多种解析解结果进行对比，指出了屈曲外压计算公式的适用范围及利用规范推荐方法进行设计时的不足；Bai[16]、Xue[17]、Toscano[18]等应用计算软件模拟了深水管道屈曲压溃和屈曲传播过程，为压溃压力和屈曲传播压力的准确预测提供了借鉴；余建星[19]、龚顺风[20]、樊志远[21]等通过建立有限元模型，开展全尺寸及缩比尺屈曲试验，研究外压作用下深海腐蚀缺陷管道的屈曲失稳机理；刘可安等[22]采用有限元软件进行二次开发，以准静态的方式模拟埋管悬跨段各参数悬跨段海底管道屈曲压溃压力的影响；刘润等[23]对比了枕木法、分布浮力法和枕木–浮力耦合法对海底管道整体屈曲变形规律的影响，研究了枕木及浮力参数对管道水平向屈曲和后屈曲的影响规律；闫行等[24]建立了柔性约束下地下储气库管柱非线性屈曲力学模型，采用慢动力法阶跃式施加管柱外载荷，分析了动态载荷作用下管柱的非线性屈曲特性；练章华等[25]基于弹塑性力学理论建立了实际井况下油管柱屈曲分析有限元模型，并在此基础上分析复杂力学工况下管柱的屈曲形态、横向位移等；武行等[26]建立含有非对称局部壁厚减薄管道在外压作用下屈曲压力理论公式，研究了局部壁厚减薄缺陷位置、长度和深度等参数对管道屈曲压力的影响；余建星等[27]通过将自定义的程序嵌入有限元软件，建立含冲刷腐蚀缺陷的海底弯管参数化模型，开展腐蚀相关参数敏感性分析，研究冲刷腐蚀弯管屈曲压力的影响。

上述研究对加劲式压力钢管等结构在发生屈曲时的临界压力、失稳模式等进行了较为全面的探讨，而采用的理论假设、边界条件和数值模型计算方式尚未统一。随着有限元软件的推广应用，本文基于特征值屈曲分析进行加劲式压力钢管管壁临界外压计算，结合Mises理论提出多环建模、分段约束的数值方法，提炼一种快捷的加劲式压力钢管临界外压计算公式，以冀为钢管抗外压稳定设计提供理论指导。

1 压力钢管管壁临界外压计算方法

1.1 解析解

根据Mises理论，加劲环间管道可以模型化为两端受约束的圆柱壳，加劲环处的钢管部位简支，其径向变形受到约束而保持圆形，轴向变形和转角不受限制，则加劲环间管壁的弹性屈曲外压可按照式（1）（以下称为Mises式）计算[15,28]：

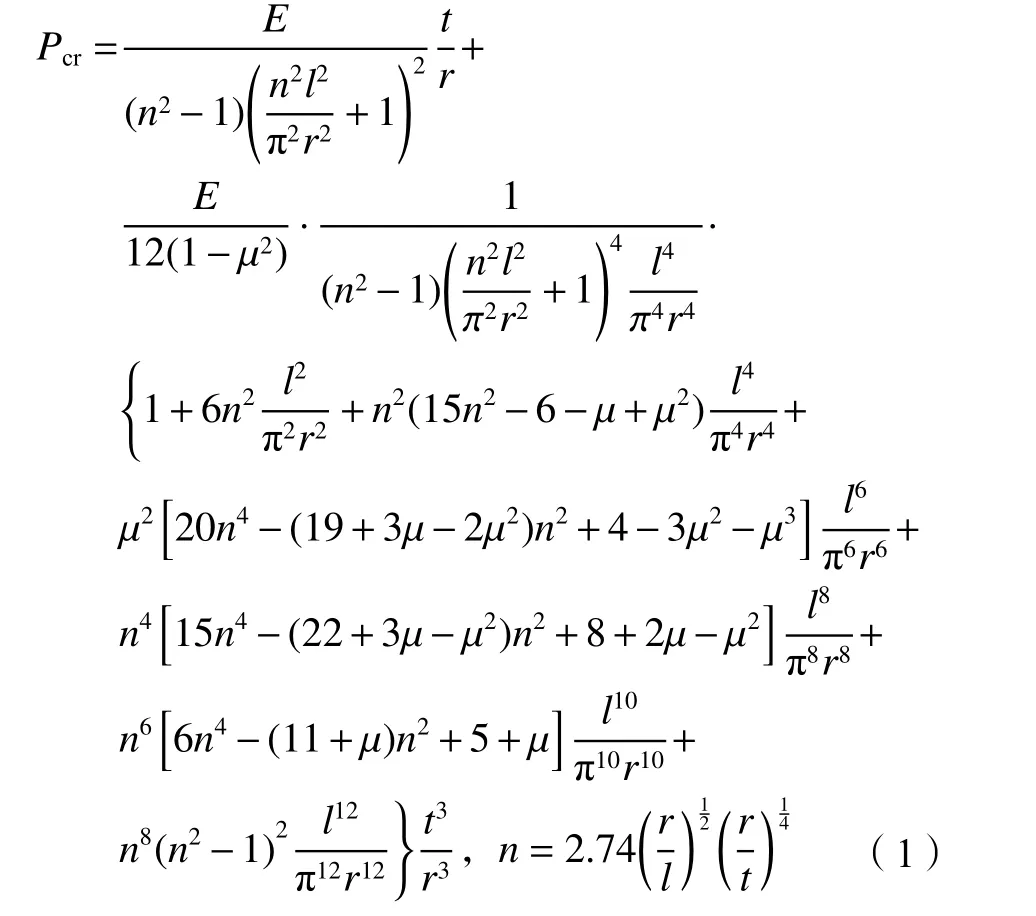
式中：Pcr为临界压力，MPa；n为相对应于最小临界压力的波数，取相近的整数；E为钢材弹性模量，MPa；r为钢管内半径，m；t为钢管管壁计算厚度，m；µ为钢材泊松比；l为加劲环间距，m。

为了便于应用，中国相关设计规范[29]将上述Mises式进行简化，所采用的加劲环间管壁临界外压表达式（以下称为规范式）为：

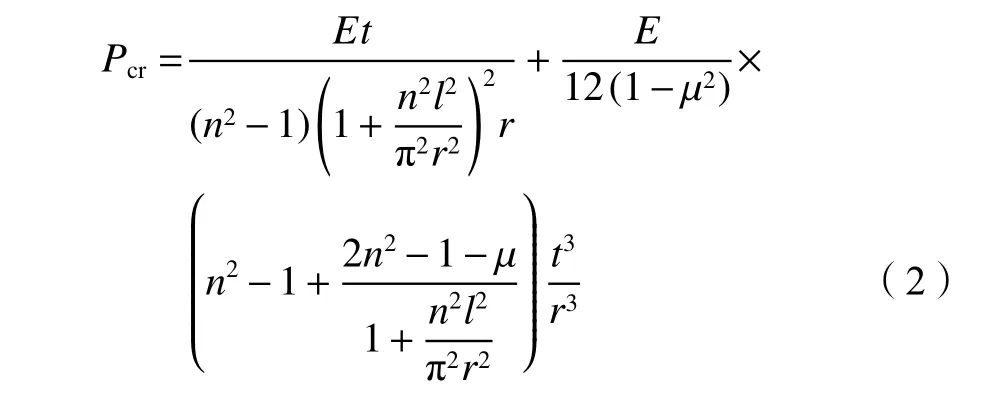
1.2 有限元特征值屈曲分析

屈曲分析是一种用于确定结构开始变得不稳定时的临界荷载和屈曲模态形状（结构发生屈曲响应时的特征形状）的技术；特征值屈曲分析可用于一个理想弹性体结构的理论屈曲强度，不考虑任何材料的初始缺陷和非线性特征，利用该方法可以了解屈曲形状和预测出屈曲荷载的上限。

特征值屈曲分析的主要目的是通过求解相关的特征值问题来获得临界屈曲载荷因子。对于屈曲分析，特征向量（模态振型）被归一化到统一，其中，最大平动自由度被设为1（质量归一化不适用于屈曲分析），模态振型是屈曲变形的精确表征。特征值分析默认提取结构振动的固有模态，临界荷载即为最小特征值×摄动荷载。

1.3 对比验证

以加劲式压力钢管为例，基于有限元软件ABAQUS对不同参数下的钢管进行3维建模，钢管半径r分别取2.0、2.5、3.0 m，加劲环间距l分别取1.0、1.5、2.0、2.5、3.0 m，厚度t取0.02 m，模型轴向长度L取15倍加劲环间距长度；钢管采用shell单元模拟，弹性模量Es=206 GPa，泊松比µ 取0.3，有限元模型如图1所示。参照Mises假定，在加劲环的几何部位施加径向约束（无实体加劲环），加劲环之间管壁中部断面施加轴向约束，模型两端面施加全约束；为确保计算精度，有限元网格最大为0.05 m。

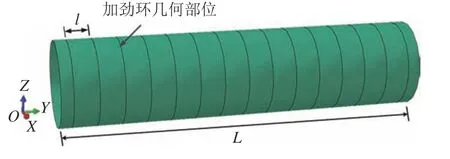
图1 有限元数值模型Fig.1 Finite-element numerical model

将分别利用规范式[29]、Mises式及有限元计算得到的钢管临界外压Pcr–1、Pcr–2、Pcr–0，以及利用式（1）计算得到的理论屈曲波数n、有限元屈曲波数n0及有限元计算相对误差δn列于表1中。

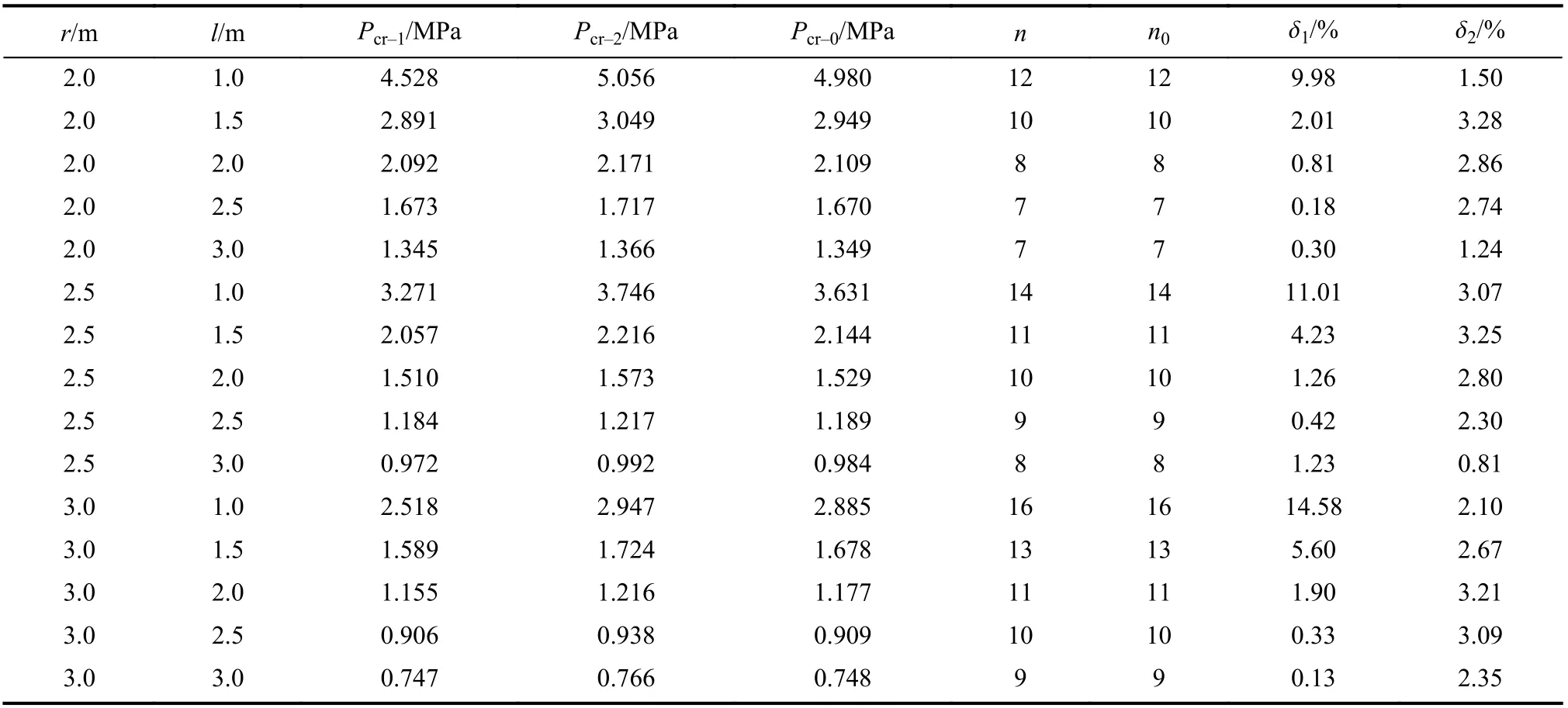
表1 临界外压计算结果Tab.1 Critical external pressure Pcr of different method

表1中，临界外压下的相对误差δn表示为：

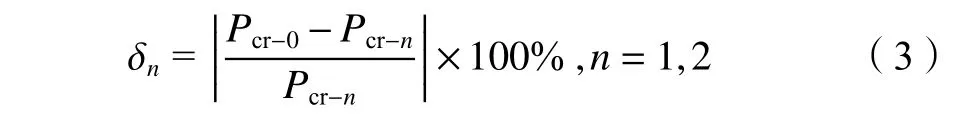
图2为根据表1中数据所绘的不同计算参数下压力钢管屈曲的临界外压计算结果对比。由此可知：有限元特征值屈曲计算的不同参数下钢管的屈曲波数与解析解保持高度一致，而随着屈曲波数的增加，规范式与Mises式计算结果差别明显增大；有限元临界外压计算结果总是介于规范式、Mises式计算结果之间，与规范式的相对误差存在较大的波动，而与Mises式计算结果的相对误差总体保持在3%左右，数值上差别较小（最大约0.1 MPa）。因此，可以说明有限元特征值屈曲计算具有较高的准确度，与Mises式解析解能保持较好的一致性，而规范采用的规范式计算结果会随着钢管屈曲波数的变化与Mises解存在较大的波动。

图2 临界外压计算结果对比Fig.2 Comparison of calculation results of critical external pressure

2 约束环境对管壁临界外压的影响

某水资源配置工程输水隧洞采用加劲式压力钢管，其几何尺寸如图3所示。钢管半径r=2 600 mm，管壁厚度t=20 mm，加劲环高度h=1 200 mm，加劲环厚度a=18 mm，加劲环间距l取1 500 mm。压力钢管材质为Q345R，弹性模量Es=206 GPa，泊松比µ 取0.3，屈服强度σs=325 MPa。

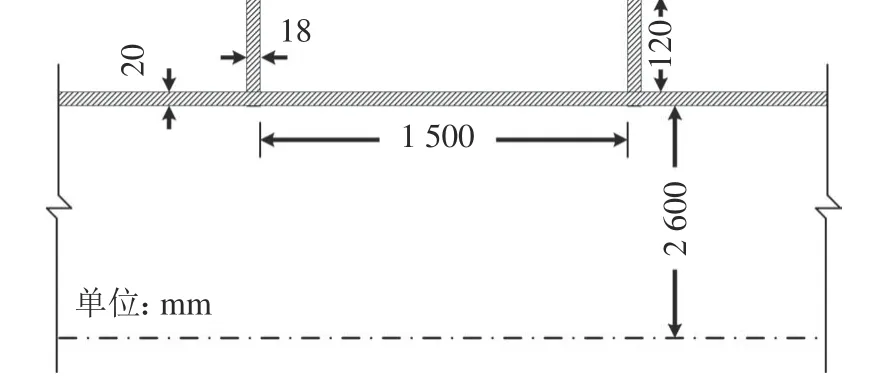
图3 钢管尺寸示意图Fig.3 Axial section of the penstock

有限元计算得到的加劲环间钢管第1阶屈曲模态如图4所示，轴向上加劲环之间含有半个波，环向上均匀分布有12个波，各个方向上依次凸出和凹陷，计算得到的钢管临界外压为2.071 MPa，而规范式、Mises式计算结果为1.971 MPa和2.111 MPa。

图4 钢管屈曲模态Fig.4 Buckling mode of the penstock

分别提取轴向、环向上波峰（波谷）所在管壁断面上所有节点的相对变形值f(x)、f(θ)进行曲线拟合，得到公式如下：

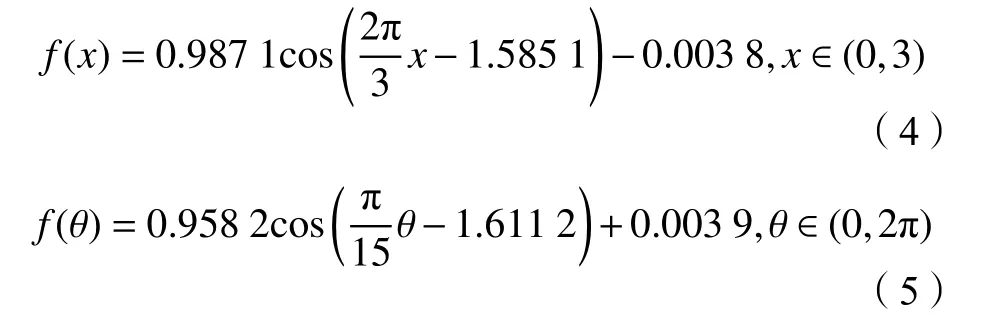
针对工程实际，考虑加劲环位置不同约束条件及实体加劲环有无对钢管临界外压计算结果的影响，在有限元模型中加劲环部位设置3类约束方案，并在每种约束方案下针对实体加劲环的有无设置两种计算条件，对比分析加劲环钢管的临界外压，具体约束方案见表2，其中，方案A为无实体加劲环，方案B为实体加劲环。

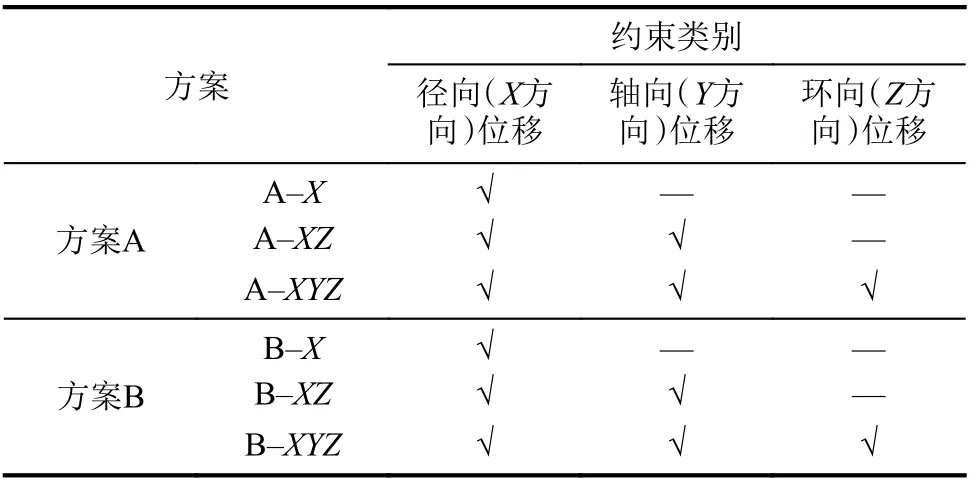
表2 计算模型的约束方案Tab.2 Constraint schemes of finite element model

除表2中所列外，所有方案在模型端部施加全约束，加劲环间管壁施加轴向位移约束。得到的钢管临界外压与模型长度关系曲线如图5所示。

由图5可知：当模型长度增加到14倍加劲环间距时，所有方案得到的钢管临界外压趋于稳定；随着加劲环位置约束作用的提高，钢管临界外压逐渐增高；当模型中实体加劲环存在时，会导致钢管临界外压计算结果相对于无实体加劲环有所增大，全约束方案B–XYZ得到的钢管临界外压最大；不设置实体加劲环的径向约束方案A–X最终得到的钢管临界外压最为接近规范式计算结果，但依旧略大于其结果，误差为5.02%；设置实体加劲环的径向约束方案B–X最终得到的钢管临界外压最为接近Mises式计算结果，但依旧略小于其结果，误差为0.81%。

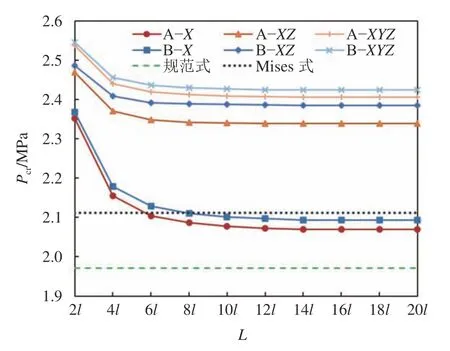
图5 临界外压与模型长度关系曲线Fig.5 Relation curves of critical external pressure andmodel length

3 临界外压快速计算方法

对于加劲式压力钢管而言，加劲环的间距l增大到一定程度后，钢管的临界外压不再发生变化，加劲环管的屈曲变形与光面管接近，此时的加劲环间距可认为是加劲环临界间距，即有效约束长度。在有效约束长度内，可认为加劲环对压力钢管的抗外压能力有增强作用，否则可按光面管处理，光面管的屈曲临界外压公式[30]为：

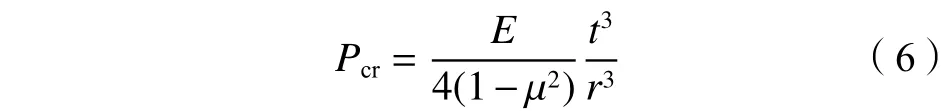
因此，按照第2节计算方案，有限元模型总长度L取20l（l最大为200 m），t取0.02 m，讨论不同管径下加劲环的有效间距。不同约束间距下管壁临界外压和屈曲波数计算结果列于表3中。

表3 不同加劲环间距下钢管管壁临界外压计算结果Tab.3 Shell’s critical external pressure for penstock with stiffening ring of different spacing

绘制临界外压变化曲线如图6所示。由图6可知：随着加劲环间距l的增大，钢管临界外压逐渐减小；而钢管半径r与钢管厚度t的比值增大同样导致临界外压的减小，并在加劲环间距为20 m之前波动较大，20 m之后基本保持稳定；钢管屈曲波逐渐减小为2个，和理论假定保持完全一致。另外，各曲线的演化规律具有一致性，最终趋近于光面管公式解析解计算结果，亦可说明实际光面管的临界外压受外部约束状态影响，当两端或其他部位存在约束时，光面管的临界外压会存在不同程度的升高。

结合表3和图6可知，加劲式压力钢管管壁临界外压与光面管临界外压存在一定的关系，结合实际工程，当加劲环间距l分别取0.5、1.0、1.5、2.0 m时，结合表3数据，参照式（5）提出加劲式压力钢管管壁临界外压快速计算公式，如下所示：

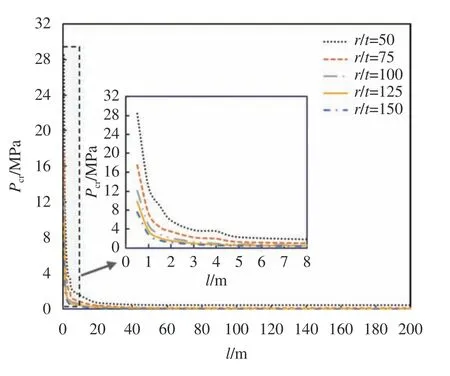
图6 临界外压变化曲线Fig.6 Variation curves of critical external pressure

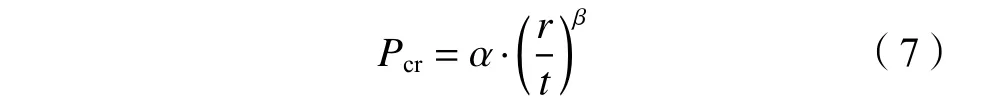
式中，系数α、β在加劲环间距l确定后进行拟合求得。当l分别取0.5、1.0、1.5、2.0 m时，相对应的系数α、β取值见表4；当l=∞时，α、β取值由光面管式（6）计算得到。

表4 公式（7）中系数取值Tab.4 Coefficient of the formula (7)

将式（7）得到的计算结果与Mises公式计算结果进行比较，如图7所示。统计后发现，本文公式与Mises式所对应曲线的拟合优度R2达到0.997以上。

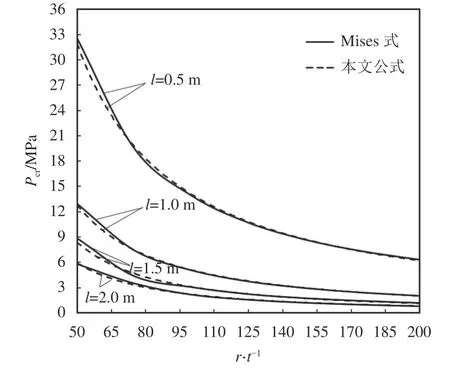
图7 两种公式临界外压计算结果对比曲线Fig.7 Comparison curves of critical external pressure calculated by two formulas

4 结 论

本文结合有限元特征值屈曲分析进行加劲式压力钢管管壁临界外压计算，对求得的钢管临界外压与解析公式计算结果展开对比讨论，并研究了不同约束条件、建模长度、加劲环间距等关键因素对管壁临界外压的影响，可以得到以下结论：

1）本文提出多环建模、分段约束计算模型得到的临界外压与Mises式解析解相对误差总体保持在3%左右；而规范采用的简化式计算结果会随着钢管屈曲波数的变化与Mises式存在较大的波动，实际工程中采用的安全系数应合理地做出调整。

2）随着加劲环位置约束作用的提高，钢管临界外压逐渐增高，而实体加劲环的建立使得钢管临界外压更接近于Mises式解析解；同时，钢管管壁临界外压随着加劲环间距、钢管半径与钢管厚度比值的增大而逐渐减小，并当加劲环间距大于20 m后不再有明显约束作用。

3）本文提出的压力钢管管壁临界外压快速计算公式，与解析解所对应曲线的拟合优度达到0.997以上，可为实际工程中管壁临界外压的计算提供新的选择。