土质场地地面爆炸当量预测方法*

张亮永，卢强，肖卫国，唐仕英，王敏超，方厚林，张德志

1. 国防科技大学气象海洋学院，湖南 长沙 410073

2. 西北核技术研究所，陕西 西安 710024

快速预测地面爆炸对工业爆炸事故评估［1-2］、恐怖袭击监测［3］、武器效能判定［4］等具有重要意义。地面爆炸能量会耦合到空气中产生扰动，随着传播距离增加由冲击波衰减成声波向远处传播。因此，可通过声学数据携带的爆源信息来反演地面爆炸当量［5-13］。其基本思路为通过缩比定律建立当量和超压峰值、正向声冲量等波形特征量之间的对应关系（即声学模型），利用远场测点数据估计相似场地的爆炸当量。

目前，声学模型分为适合快速计算的经验或半经验模型［3，6-7，11，14-19］和综合考虑波形参数的全波形反演模型［10，12-13，19］。全波形反演模型能够对波形特征进行更全面描述，但影响波形因素较多，计算量较大［5，9-10，12］。而经验和半经验模型可以快速预测源参数或测点波形参数且精度较高，该模型得到不断 发 展，相 继 提 出ANSI 模 型［7，14，20］、KG85 模型［15］、BOOM 模型［7，16］、地面爆炸声学模型［3］和IPM参数模型［6］。但以上方法因没有考虑爆炸能量耦合到地下影响，辐射到空气中的声能只表征部分爆炸威力。而爆炸耦合的声能和爆源位置密切相关，尤其在地表附近，由地面爆炸到浅埋爆炸耦合到空气中的能量可以产生量级上差别［17-19，21］。由此，不同岩土介质的近地面爆炸声学模型得到发展［17-19，21］。但由于爆炸耦合到空气中的能量和爆源位置、爆炸当量有关，不同当量和爆高的爆源在相同爆心距处可以产生相同的超压波形参数，因此反演结果会存在明显的当量-爆高（埋深）折中关系，需要额外的爆高（埋深）约束才能确定爆炸当量。

Bonner 等［22］提出通过地震波模型提供额外约束，采用相对误差法融合声和地震波数据，对硬岩场地地面爆炸当量声震进行分析；文献［17，23］基于HRI（Humble Redwood I）、HRII等系列化爆试验建立了土质场地近地面爆炸声震模型，获得了较高的地面爆炸当量预测精度；Pasyanos等［19］基于SPE（source physics experiment）、FSE（forensics surface events）等系列化爆试验建立了硬岩场地近地面爆源参数声震分析方法，解决了硬岩场地的当量反演问题，但涉及到复杂的全波形反演算法，难以实现爆源参数的快速预测；文献［18，21］对声震分析方法进行了更进一步的研究，通过改进声震模型和数据融合算法提高源参数估计精度。

为实现地面爆炸当量快速预测，本文基于某土质场地化爆实验的声震数据，考虑地面反射和地介质耦合作用，对以经验和半经验声学模型为基础的地面爆炸当量预测方法进行了讨论，并结合地震波模型采用声震分析方法分析了地面爆炸当量预测精度。

1 实验介绍

3 组地面爆炸实验中地质为土，炸药为TNT，TNT当量为50 kg。气象条件为温度22.5 ℃，气压920 hPa，轻风，声学测点6个，地震测点3个，地震与声测点共址，测点分布和距离见图1和表1。

图1 测点分布Fig.1 Distribution of measuring points

表1 测点距离Table 1 Distances of measuring points

2 基于声学模型的当量反演分析

2.1 方 法

基于自由场经验或半经验声学模型得到传播距离、TNT当量与波形特征量（超压峰值、声冲量等）之间的关系；并考虑地表界面反射和地介质耦合作用，得到实测波形特征量、TNT当量和传播距离的理论关系。以波形特征量预测值和实测值的最小误差为准则，采用格点搜索法获取TNT 当量的最优解。

超压峰值和声冲量是常用的两个波形特征量。以超压峰值为特征量的自由场声学模型主要有5种，包 括KG85 超 压 模 型［15］、BOOM 超 压 模 型［7，16］、ANSI-Arrowsmith 超 压模型［7，14］、ANSI-Ford 超压模型［14，20］和IPM 超压模型［6］等；以声冲量为特征量的自由场声学模型主要有2 种：KG85 声冲量模型［15］和ANSI-Ford 声冲量模型［14，20］，模型公式见表2。表中p为超压峰值（Pa），ps为比超压峰值（Pa），Pobs为环境大气压（Pa），r为距离（m），rs为比距离（m·kg-1/3），W为TNT 当量（kg），is为比声冲量（Pa·s·kg-1/3）。

表2 自由场声学模型Table 2 Free-field acoustic model

爆源靠近地面时，地面反射作用和地介质耦合作用会明显影响爆炸产生的超压波形参数［17-21，25-27］。对于地面反射作用，爆源放置在刚性地面时等效TNT当量为实际TNT当量的2倍。爆源位于刚性地面以上位置时，等效TNT 当量和爆高（HOB，height of burst）存在以下关系［20，25-26］

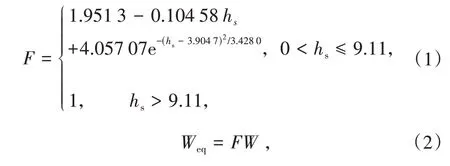
式中F为等效当量因子，hs为比爆高（m·kg-1/3）。

近地面爆炸存在明显的地介质耦合作用，爆炸产生的能量同时耦合到空气和地介质中分别形成声波和地震波向远处传播［17，19，21-22，27］。通过对-1.6～0.9 m/kg1/3比爆高区间的大量声学数据进行分析，发现超压峰值、正向声冲量等波形特征量和爆高（埋深）、距离存在以下关系（称为近地面声学模型）［17-18，21］，即

式中qs为比特征量，对应比声冲量is（Pa·s·kg-1/3）或比超压峰值ps（Pa）；α1、α2和α3为待定系数，和地质特性相关。考虑大气环境的影响，Sachs 给出以下缩比关系［24］，即

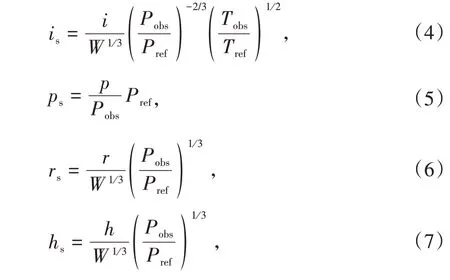
式中Pref为参考大气压（Pa），取101 325 Pa，Tobs为环境温度（K），Tref为参考环境温度（K），取288.15 K。

Ford 等［17］获取了大量土质场地近地面爆炸声学数据，由此确定了土质场地超压峰值和正向声冲量近地面声学模型系数，见表3。

表3 土质场地模型系数Table 3 Model coefficients of soil site

进一步地，将近地面声学模型改写为

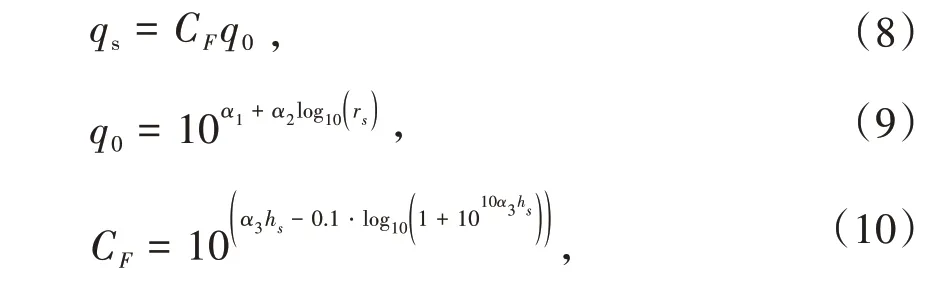
式中q0为爆高趋于无穷的近地面声学模型，CF为声耦合系数。近地面声学模型是由比爆高小于0.9 m/kg1/3的近地面化爆声震数据拟合得到，而在该比爆高区间内等效当量因子接近常数2，表明该比爆高区间内地面反射作用基本保持不变，即该比爆高区间内特征量变化仅表征爆炸能量耦合到地下的影响。当比爆高值越来越大时，爆炸能量耦合到地下影响越来越小（即声耦合系数接近1），但地面反射作用即等效当量因子先增大后减小。根据土质场地声耦合系数和等效当量因子计算公式，比爆高大于9.11 m/kg1/3时，声耦合系数和等效当量因子都为1，此时声传播模型为自由场模型。基于以上分析，q0为仅考虑地面反射影响的声学模型，由等效TNT当量代入自由场声学模型得到。根据近地面声学模型，不同埋深地下爆炸的声学模型通过声耦合系数等效成地面爆炸声学模型，对地下爆炸等效当量因子取2，得到不同爆高（埋深）的等效当量因子

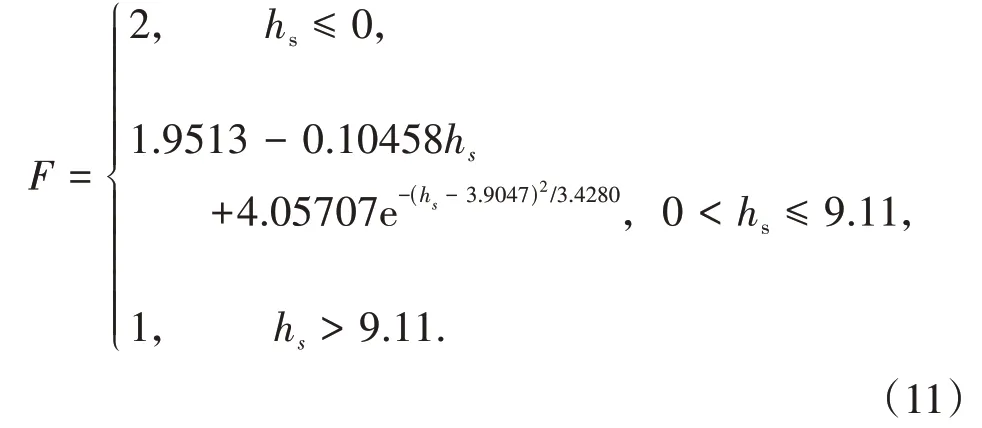
建立不同TNT当量的波形特征量预测值和实测值的误差关系，采用格点搜索法以最小误差为准则得到最优TNT当量值

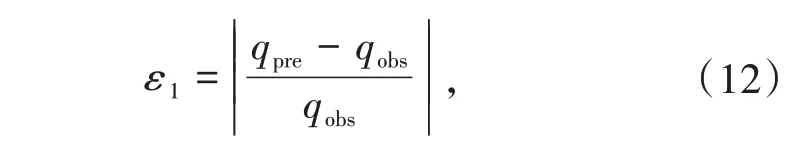
式中qpre和qobs分别为波形特征量的预测值和观测值。

2.2 讨 论

基于声学模型的TNT当量反演结果如图2～4所示。由图可知，3发TNT当量相同爆源的反演结果基本一致，表明重复性较好、数据有效；还发现TNT当量和埋深之间存在明显折中关系，最小误差分布在折中曲线上，需要额外的爆高约束才能确定TNT当量值。由折中曲线可知，爆源位于地面之上时TNT当量随爆高基本保持不变，且明显小于实际TNT当量。随着爆源靠近地面直至位于地下，TNT当量随爆高发生明显变化，随着埋深增加TNT当量迅速变大。这表明：爆源位于地面之上时，TNT当量对爆高变化不敏感；爆源位于地下时，爆源埋深会明显影响TNT当量预测值，且随着埋深增加影响更大。

图2 基于声学模型的EX01爆源TNT当量预测结果Fig.2 EX01 explosion yield predicted by acoustic models

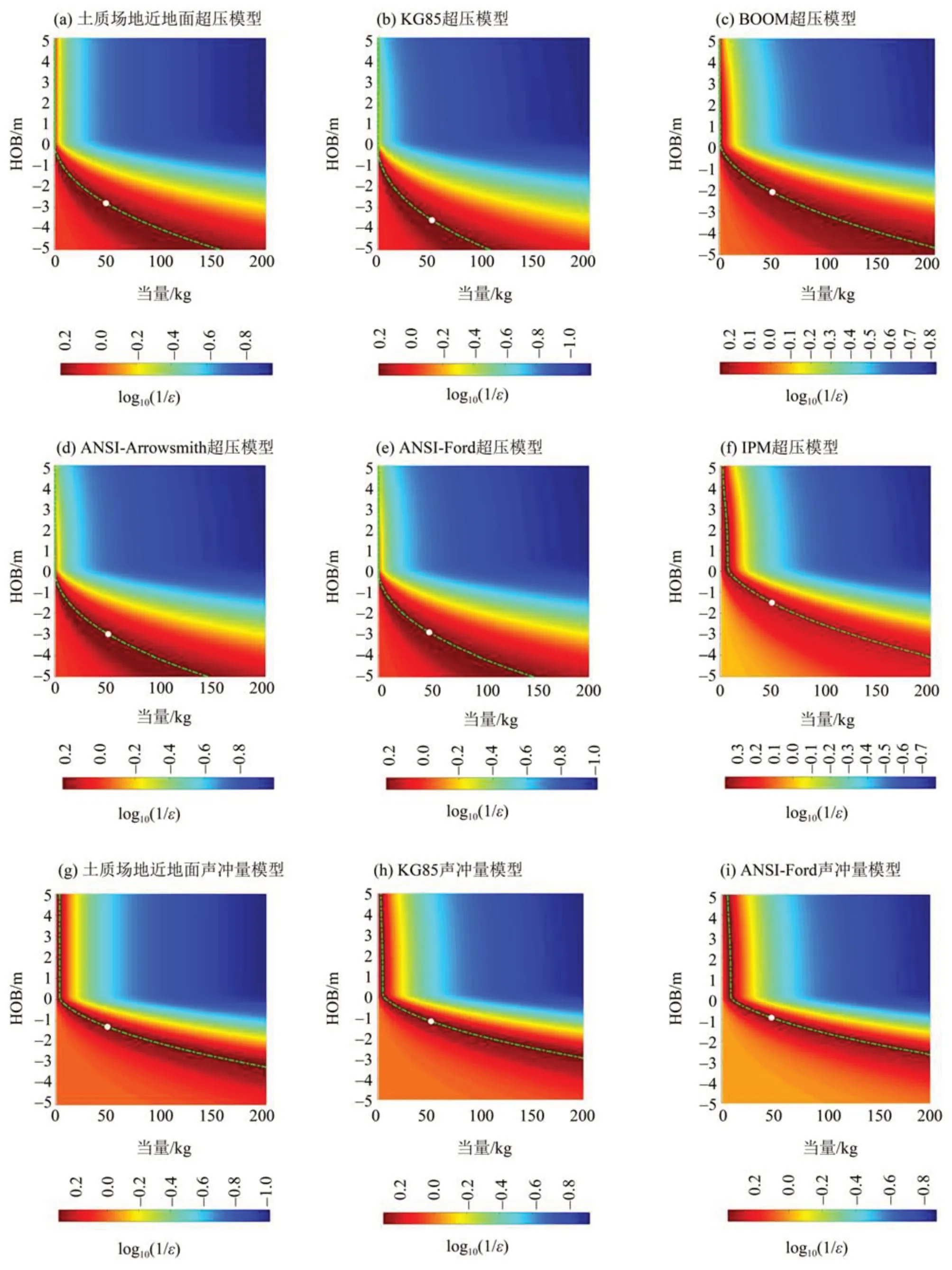
图3 基于声学模型的EX02爆源TNT当量预测结果Fig.3 EX02 explosion yield predicted by acoustic models

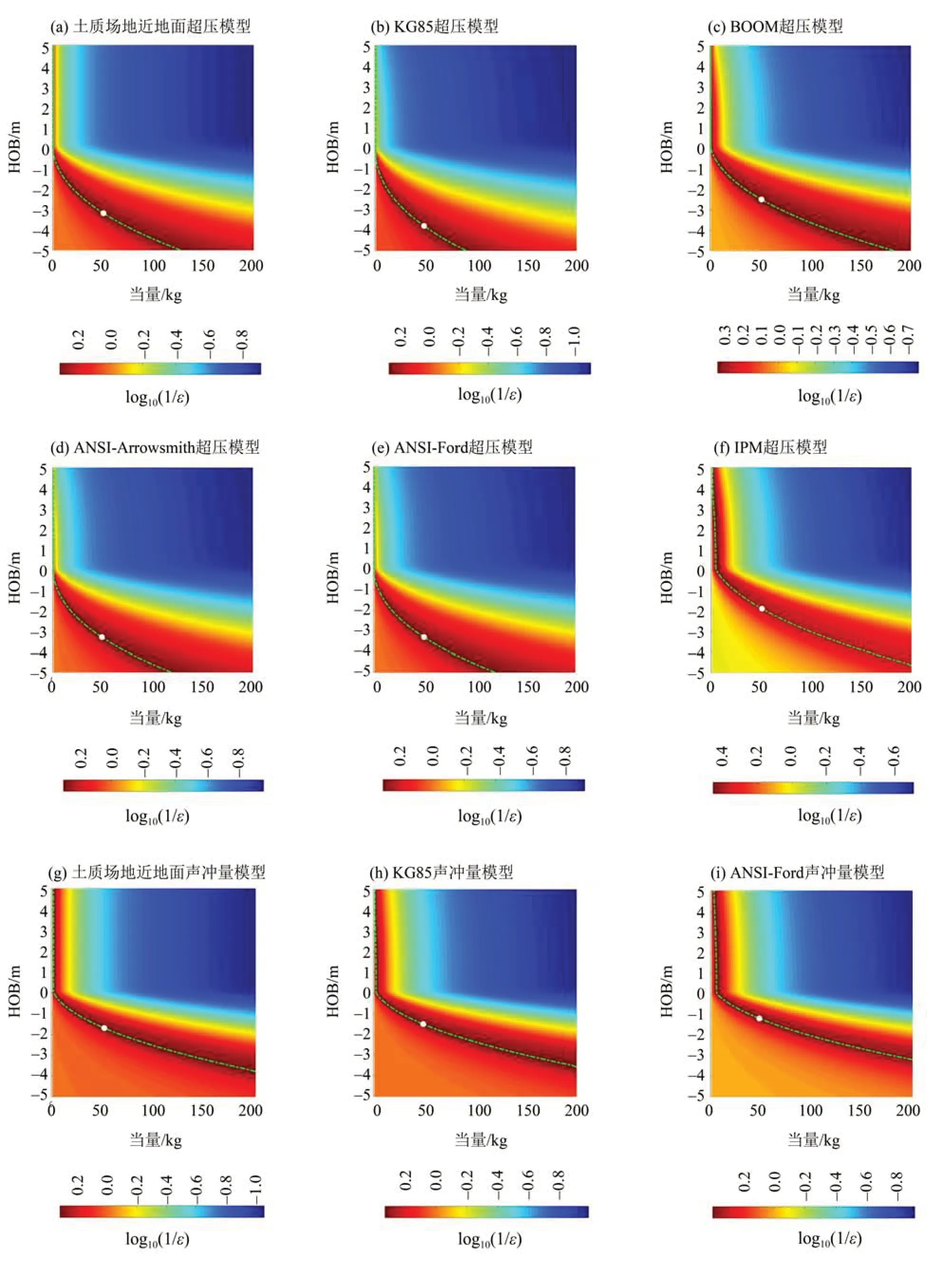
图4 基于声学模型的EX03爆源TNT当量预测结果Fig.4 EX03 explosion yield predicted by acoustic models

对比不同模型的折中关系，如图5所示。从图中可以看出，IPM超压模型相对其余超压模型受爆源位置影响更大，ANSI-Ford声冲量模型折中曲线在所有模型中相对爆高变化最陡，即受爆源位置影响最大。IPM超压模型和爆源位置的关系在爆高>0时和声冲量模型较接近，在爆源位于地下时变化趋势相对声冲量模型更缓，IPM超压模型和声冲量模型存在交叉。总体上，相对超压模型声冲量模型反演爆源TNT当量受爆源位置影响更大。

图5 基于声学模型的折中曲线Fig.5 Trade-off curves by acoustic models

对于地面爆炸，通常将地表假设为刚性界面，不考虑爆炸能量耦合到地下，等效TNT当量为2倍实际当量［5，10，12］。由此得到的TNT 当量预测结果，如表4所示。由表可知，基于声学模型的TNT当量估计结果明显小于真实值，误差较大。这是由于上述过程对应爆高为0、声耦合系数为1 的情况，而根据现场爆坑情况，爆炸产生了明显土坑，表明爆炸部分能量耦合到土介质中，并没有完全耦合到空气中，声耦合系数应＜1。

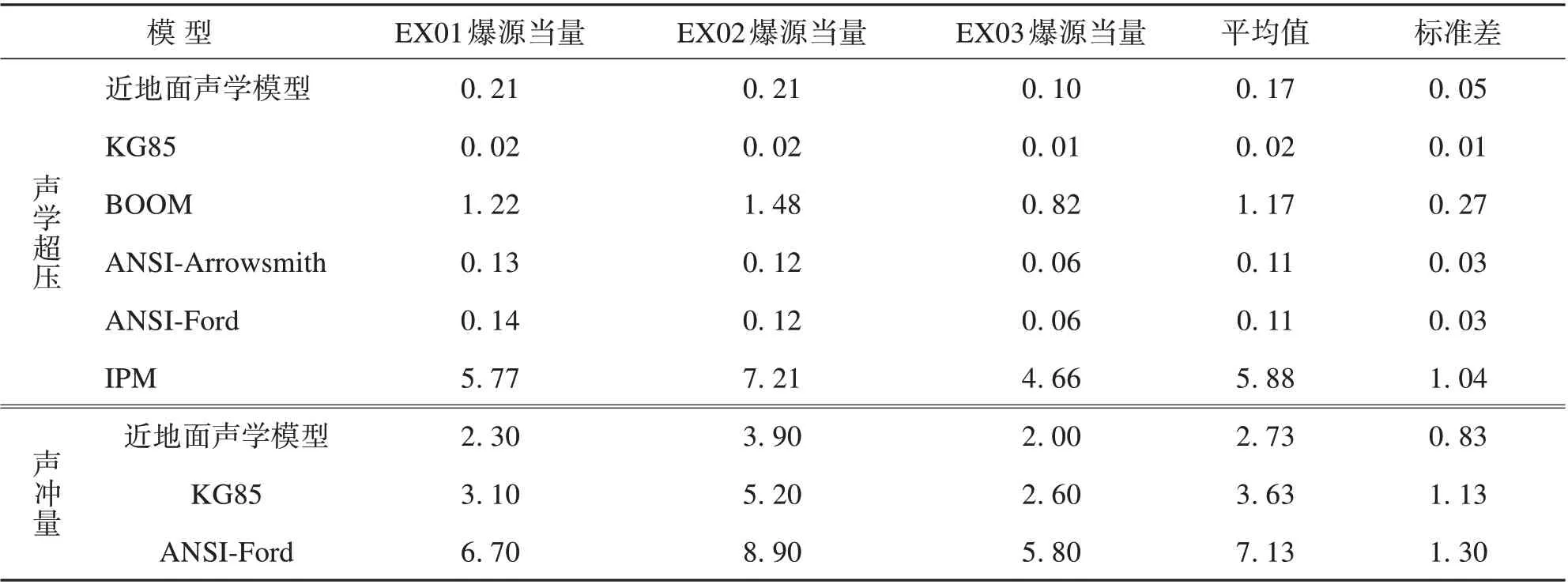
表4 基于声学超压模型和声冲量模型的TNT当量估计结果1）Table 4 Explosion yields predicted by acoustic overpressure models and acoustic impulse models kg

表5 为基于实际爆源当量反演得到的爆源埋深和声耦合系数。由表可知，爆源的等效埋深大于0，声耦合系数明显小于1。其中，相对其余超压模型IPM超压模型反演得到的埋深和标准差最小、声耦合系数最大；在所有模型中ANSI-Ford声冲量模型反演得到的埋深和标准差最小、声耦合系数最大。

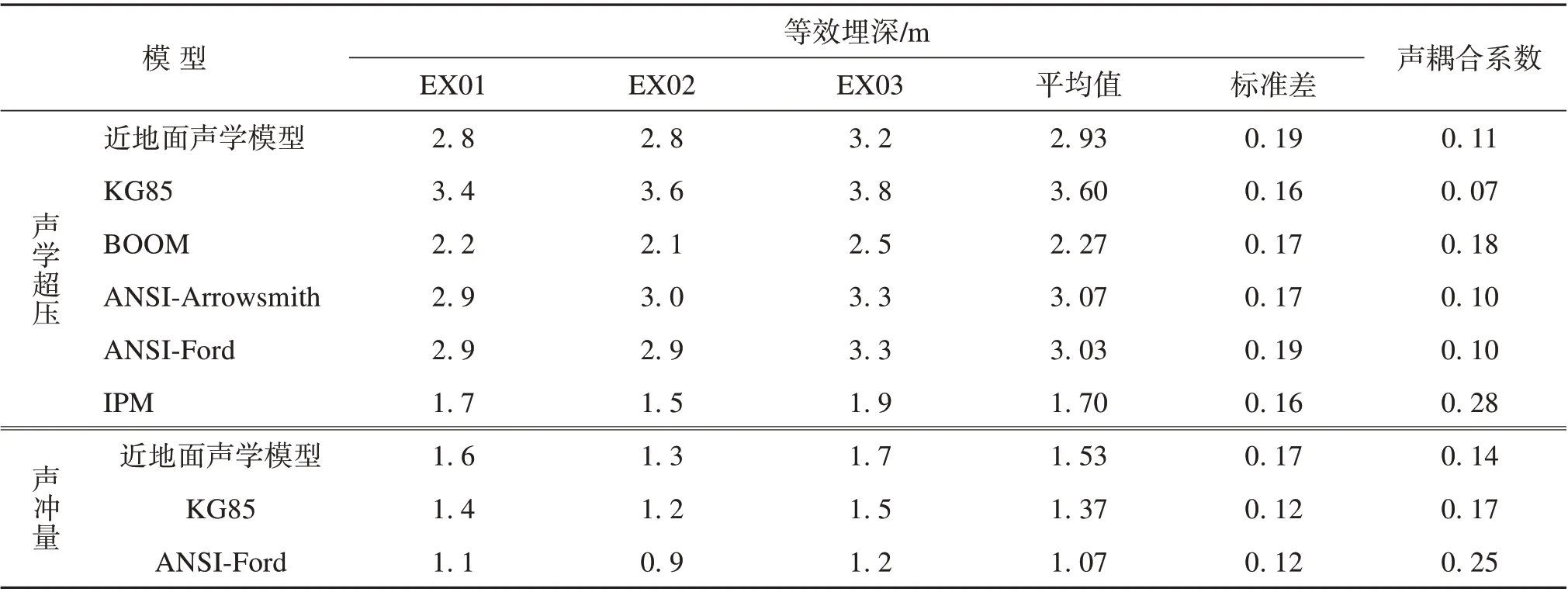
表5 基于声学超压模型和声冲量模型反演的埋深和声耦合系数Table 5 Burial depth and acoustic coupling coefficient corresponding to real yield predicted by acoustic overpressure and impulse models

3 基于声震分析方法的TNT 当量反演

3.1 声震分析方法

声震分析方法基于数据融合方法、利用地震波（地运动）数据和声学（空气超压）数据，通过大气和地介质中的波动信息对源参数进行多重约束，以综合分析爆源参数［17-19，21］。声震分析方法包括声学模型、地震波模型和数据融合方法。

对于地震波模型，研究表明：采用P波位移首峰值对爆源参数进行反演，比采用速度、加速度等波形参数更为稳健。P 波位移首峰值和TNT 当量、距离之间的关系为［17，18，23］

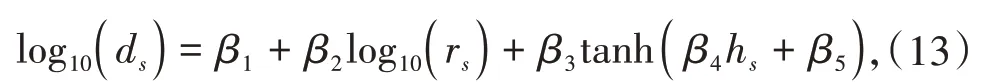
式中ds为比位移（m/kg1/3）；β1、β2、β3、β4和β5分别为待定系数，和地质特性密切相关。根据Sachs 缩比关系［24］，比位移为相对误差法是数据融合的常见方法［22］。建立不同TNT当量的声震波形特征量预测值和实测值误差关系，赋予声震相对误差权重，采用格点搜索法以最小误差为准则得到最优TNT当量值。声震数据的综合误差为

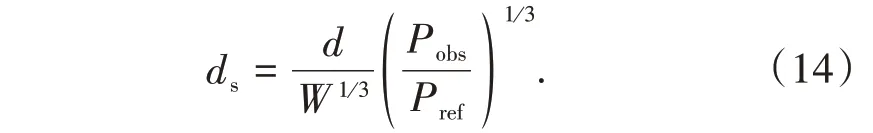
式中j为声学方法类型；N为融合的声学方法数量；wd和wi分别为地震波和声学数据的权重，取为0.5。

3.2 讨 论

图6～8为基于声震分析方法的源参数误差分布。由图可知，声学模型和地震波模型分别存在一条折中曲线，且两者会存在交叉，交叉位置的相对误差最小；由此破除了TNT 当量和埋深之间的折中关系，可以得到确定的TNT当量估计值。

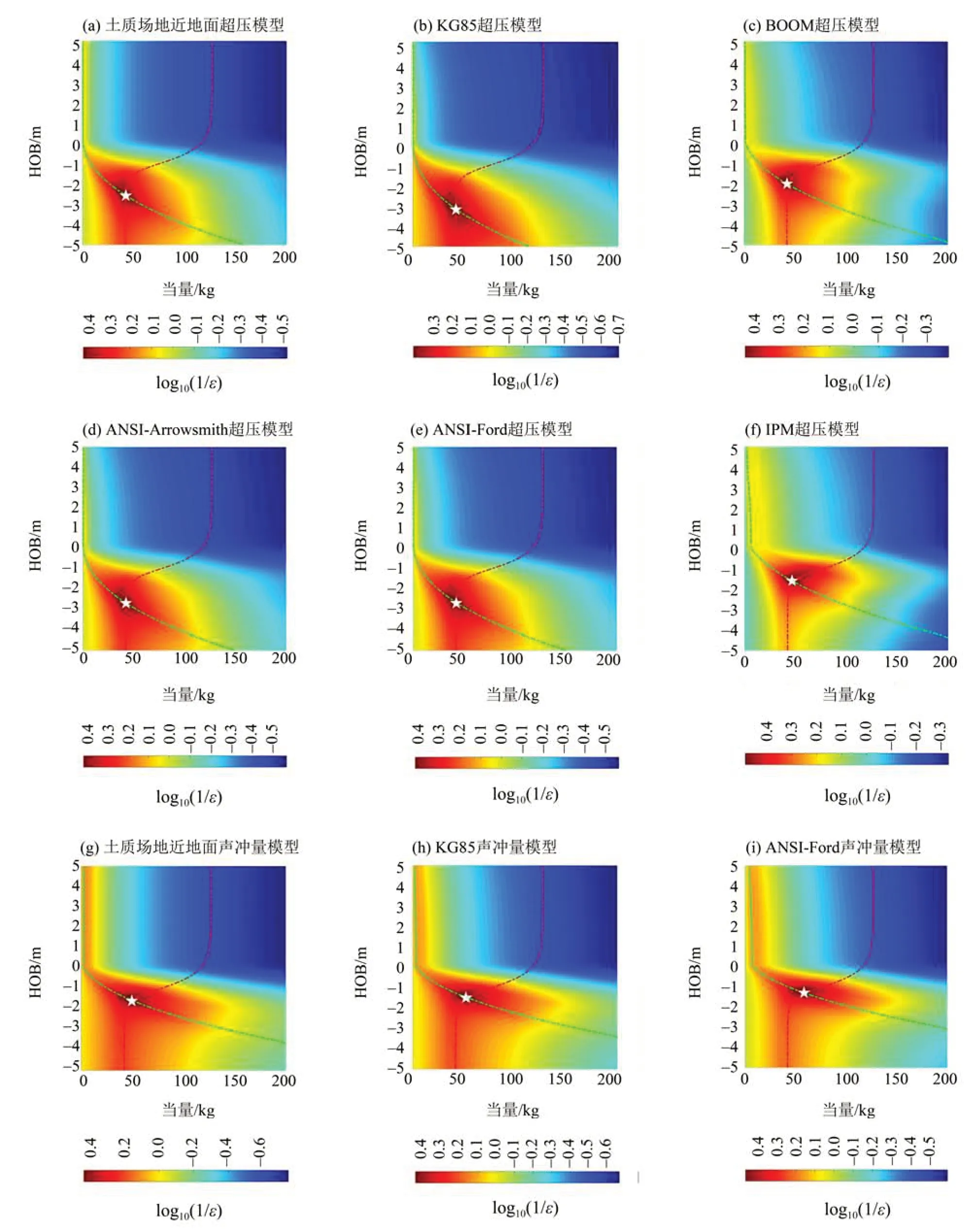
图6 EX01的声震分析结果Fig.6 EX01 explosion yield predicted by seismoacoustic analysis

基于声震分析方法的TNT当量反演结果见表6。由表6可知，基于超压模型的声震分析结果相对误差不超过16%，基于声冲量模型的声震分析结果相对误差不超过23%。这表明采用声震分析方法预测地面爆炸TNT当量可以获得较高的预测精度。对比基于超压模型的声震分析结果，发现IPM超压模型的声震分析方法精度最高，相对误差不超过4%，但不确定度较大。对比基于声冲量模型的声震分析结果（表6），发现近地面声学模型的声震分析方法精度最高、不确定度最小，且精度高于IPM超压模型的声震分析方法。以上表明，基于IPM超压模型和近地面声冲量模型的声震分析方法具有较好的TNT当量预测性能。

表6 基于声学超压模型和声冲量模型的声震分析反演结果1）Table 6 Seismoacoustic analysis results based on acoustic overpressure models and acoustic impulse models

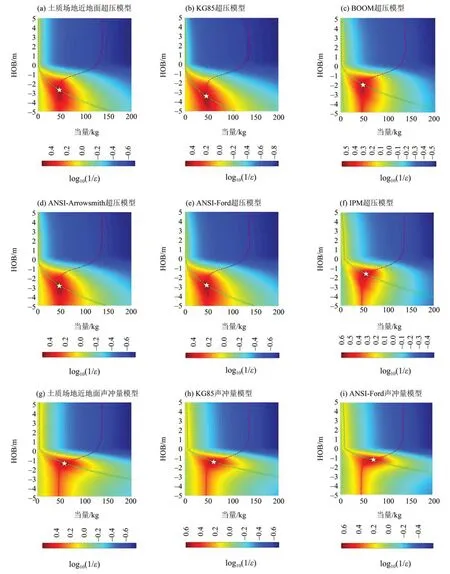
图7 EX02的声震分析结果Fig.7 EX02 explosion yield predicted by seismoacoustic analysis

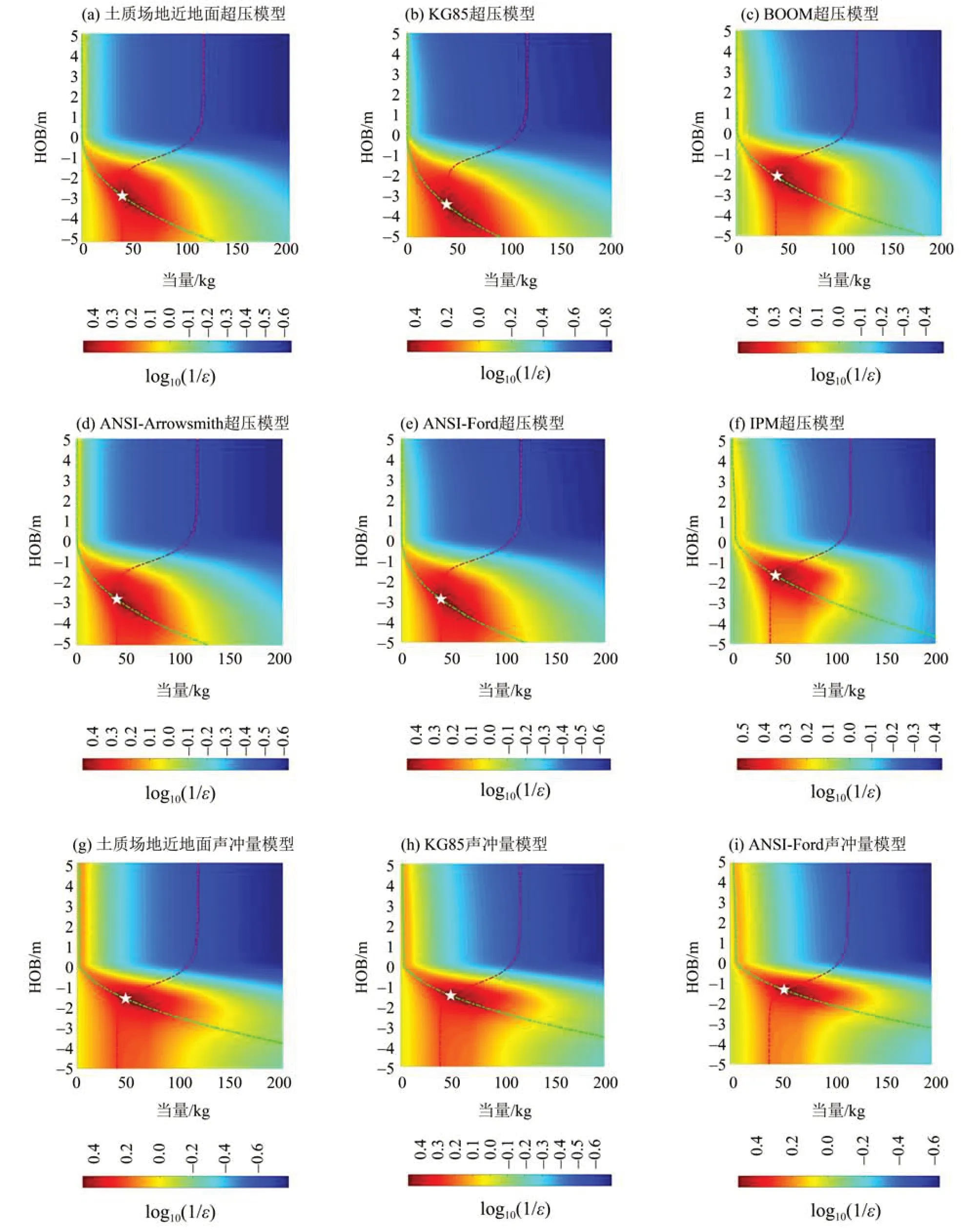
图8 EX03的声震分析结果Fig.8 EX03 explosion yield predicted by seismoacoustic analysis

联合所有声学模型和地震波模型进行声震分析，得到反演的EX01、EX02、EX03爆源当量分别为43.6、45.5 和39.7 kg，均值42.93 kg，标准差2.41 kg，相对误差14.13%。结果还显示，联合TNT当量预测的精度介于单一声学模型的预测精度之间，但标准差最小。表明所有模型的联合反演可以减小TNT当量预测结果的不确定性，其估计精度达不到最优但不会最差。

4 结 论

本文基于土质场地化爆实验声震数据对地面爆炸当量快速预测方法进行了讨论，得到以下主要结论：

1） 地介质耦合作用声学方法地面爆炸当量预测精度影响较大。若不考虑地面耦合情况，土质场地的当量预测结果明显小于真实值、误差较大。

2） 声学方法预测地面爆炸当量受到当量-爆高折中关系的限制，无法确定具体的当量预测值。而联合地震波数据增加了额外约束，可以减小当量-爆高折中关系，获得较高的当量预测精度。

3） 对比多种分析模型，发现：采用IPM 声学模型和近地面声学模型进行声震分析，当量估计精度最高。

4） 联合所有声学模型和地震波模型进行声震分析，可以减小当量估计结果的不确定性，其预测精度达不到最优但不会最差。