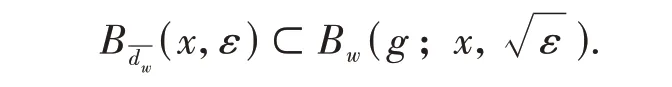非紧集上错误函数下自由半群作用的拓扑压

郭锴，肖倩，马东魁

华南理工大学数学学院，广东 广州 510641

Topological pressure，introduced by Ruelle［1］and Walters［2］，is a core concept in dynamical system and ergodic theory，and plays an important role in the study of thermodynamic formalism. From the viewpoint of dimension theory，Pesin and Pitskel［3-4］studied the topological pressure of non-compact subsets by using carátheory structure（C-P structure），and proposed the topological pressure of non-compact sets in dynamical systems，which is the generalization of Bowen's［5］topological entropy defined by non-compact sets. As the physical process evolves，it is natural for the evolution process to produce changes or some errors in the orbit calculation.However，a self-adaptable system should decrease errors over time. This prompted Cheng，Zhao et al［6］to study the dynamical systems under a mistake function. They defined the pressure for asymptotically sub-additive potentials under a mistake function，and proved that the topological pressure under a mistake function is equivalent to the topological pressure without mistake function by using the ergodic theory. Later，Chen et al［7］gave the concepts of topological pressure with mistake function and showed that the topological pressure under a mistake function on any subset is the same as the classical Pesin pressure of the subset in dynamical systems. This means that the topological pressure under a mistake function in the dynamical system is adaptive，which generalizes the result in the additive case in［3］.

With the development of research on dynamical systems，the dynamical systems of group action has attracted people's attention. To study some questions，Xiao et al［8］gave the definitions of topological pressure and upper and lower capacity topological pressures of a free semigroup action by using C-P structure，and obtained some properties of them. Naturally，we wonder if the topological pressure of free semigroup actions has the similar result in［7］. In order to answer this question，in this paper we introduce the definitions of topological pressure of free semigroup actions under a mistake function and show the topological pressure of free semigroup actions under a mistake function is the same as the topological pressure of free semigroup actions defined by Xiao and Ma［8］.

Furthermore，Gröger et al［9］showed that the entropy of the whole system with Bowen metric is equal to the entropy with mean metric. As an application，we prove that the topological pressure of free semigroup actions defined by Bowen metric coincides with the topological pressure of free semigroup actions defined by mean metric on a non-compact subset.

This paper is organized as follows. In section 1，we give some preliminaries. In section 2，we introduce two definitions of topological pressure of free semigroup actions under a mistake function and prove the main results. Finally，we give an application.

1 Preliminaries

1.1 Words and sequences

Letdenote the set of all finite words of symbols 0，1，…，m-1. For anyw∈，the length ofw，denoted by|w|，is defined the digits of symbols inw. Obviously，with respect to the law of composition is a free semigroup withmgenerators. We writew′≤wif there exists a wordsuch thatw=Forw=i1…ik∈，denotewˉ=ik…i1.

Denote by Σmthe set of all two-side infinite sequences of symbols 0，1，…，m-1，that is，

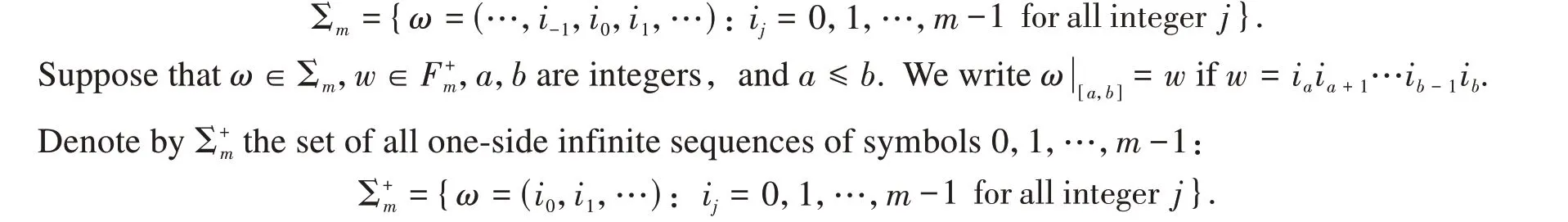
1.2 Mistake function

Let's recall the definition of the mistake function in［7］，which is a little bit different from［6，10］.

Definition 1Givenε0＞0，the functiong：N ×(0，ε0]→R is called a mistake function ifg(n，ε) ≤g(n+ 1，ε) for allε∈(0，ε0]andn∈N and

For a mistake functiong，ifε＞ε0，setg(n，ε) =g(n，ε0).

1.3 Definition of topological pressure of free semigroup actions by using open covers

Let(X，d) be a compact metric space andGbe the free semigroup generated byf0，f1，…，fm-1，wherefi(0 ≤i≤m- 1) is continuous transformations fromXto itself. Givenφ0，φ1，…，φm-1∈C(X，R)， denote Φ ={φ0，φ1，…，φm-1}. For simplicity of notation， we writefwinstead offi1∘fi2∘… ∘fin， wherew=i1i2…in∈Obviously，fww′=fw fw′for anyw，. Forw=i1i2…in∈，denote

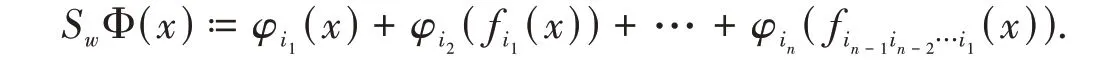
Xiao and Ma［8］introduced the notion of topological pressure of free semigroup actions by C-P structure as follows：

Considering a finite open coverUofX，write | U |= max{|U|：U∈U}，and let

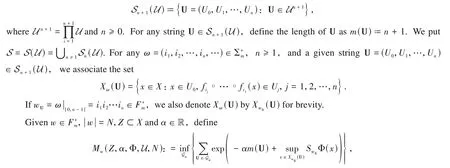
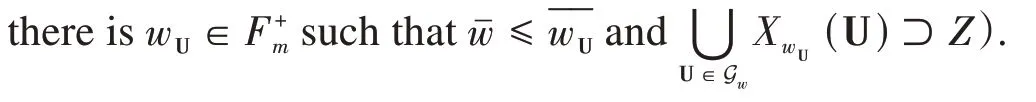
for all U ∈GwandGwcoversZ（i.e. for any U ∈Gw，

Let

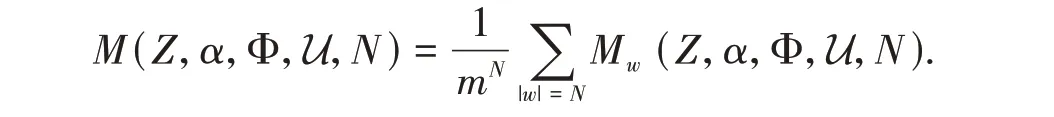
We can easily verify that the functionM(Z，α，Φ，U，N) is non-decreasing asNincreases.Therefore，the following limit exists

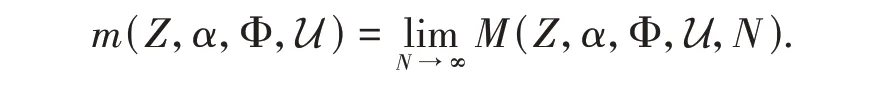
There is a critical value ofαat whichm(Z，α，Φ，U) jumps from ∞to 0. Denote

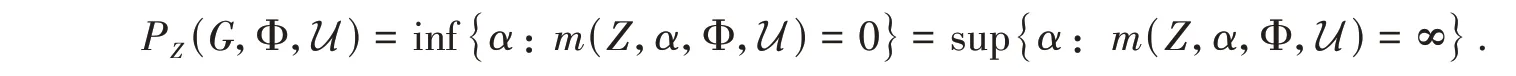
The topological pressure of a free semigroupGwith respect to Φ on the setZis

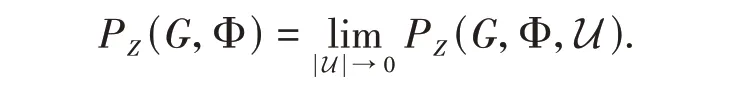
1.4 Definition of topological pressure of free semigroup actions by using the center of Bowen ball

First，recall the definitions of the Bowen metric and(w，δ)-Bowen ball.

LetXbe a compact metric space with metricd，f0，f1，…，fm-1continuous transformations fromXto itself.Suppose that a free semigroupGwithmgeneratorsf0，f1，…，fm-1acts onX. Denote Φ ={φ0，φ1，…，φm-1}，whereφ0，φ1，…，φm-1∈C(X，R). For eachw∈，a new metricdwonX（named Bowen metric）is given by

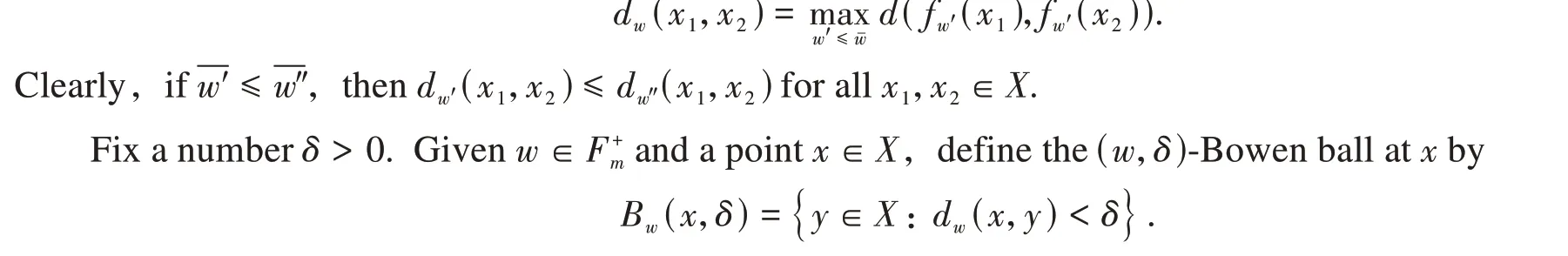
Based on the work of Climenhaga in［11］，Xiao and Ma［8］defined the topological pressure of free semigroup actions by using the center of Bowen ball. Now，let us recall the definition of topological pressure of free semigroup actions by the center of Bowen ball in［8］.

Let F denote the collection of Bowen ball，that is，

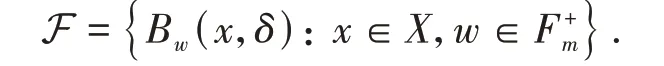
Givenw∈，|w|=N∈N，Z⊂Xandα∈R，define

Set

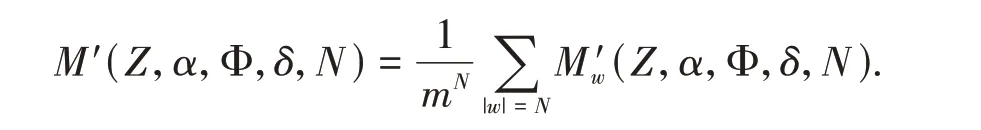
It is easy to verify that the functionM′(Z，α，Φ，δ，N) is non-decreasing asNincreases.Therefore，there exists the limit

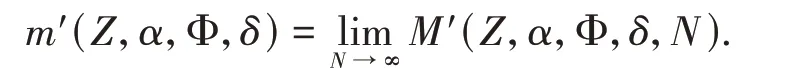
Same as above，denote the critical value ofαby

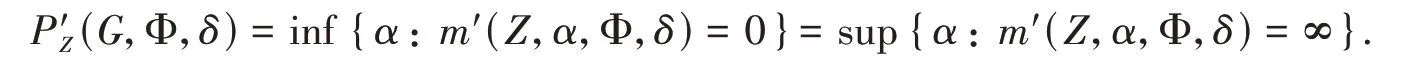
The topological pressure of a free semigroupGwith respect to Φ on the setZis

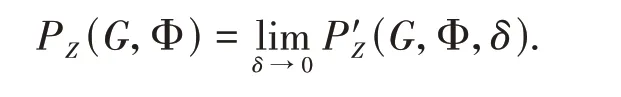
2 Main results and example

Based on ［6-7］，in this section，we first give two concepts of topological pressure of free semigroup actions under a mistake function by using open covers and the center of mistake Bowen ball respectively. In addition，we show that these two concepts are equivalent to the definitions of the topological pressure of free semigroup actions introduced by Xiao and Ma［8］. Finally，we give a notion of mean metric and show that the topological pressure of free semigroup actions under a mistake function defined by Bowen metric agrees with the topological pressure of free semigroup actions defined by mean metric.

Letf0，f1，…，fm-1be the continuous transformations from compact metric space (X，d) to itself. DenoteGthe free semigroup withmgeneratorsf0，f1，…，fm-1acting onX. Givenφ0，φ1，…，φm-1∈C(X，R)，denote Φ ={φ0，φ1，…，φm-1}.

2.1 Definition of topological pressure of free semigroup actions under a mistake function by using open covers

Considering a finite open coverUofX. For any string U ∈Sn+1(U)，let

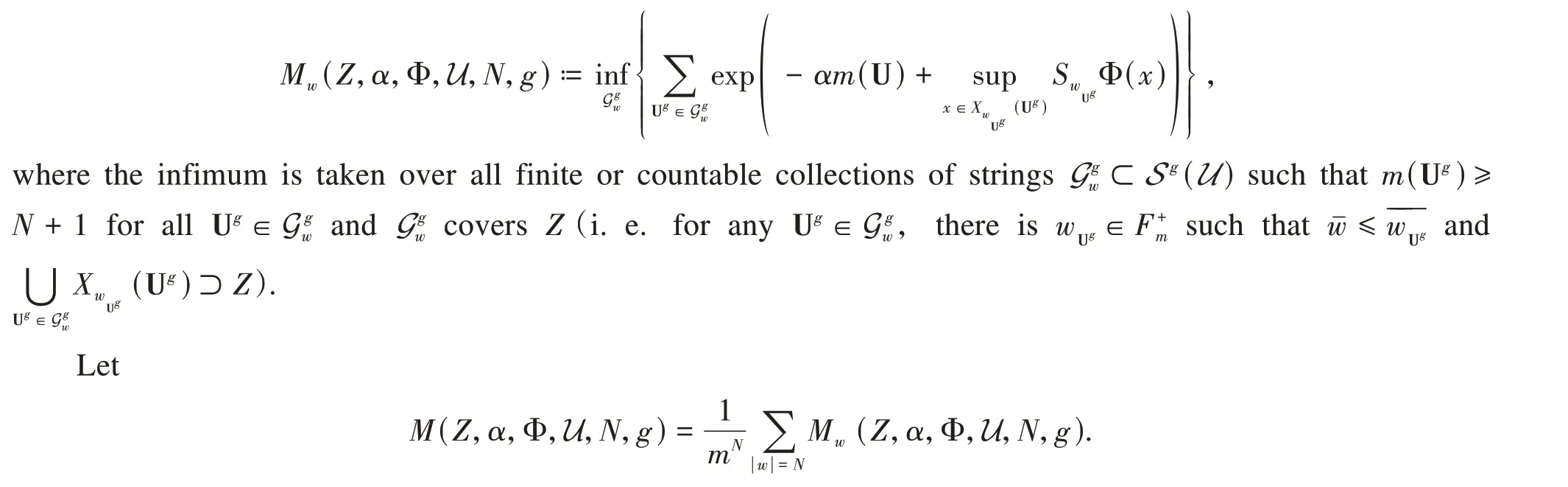
We can easily verify that the functionM(Z，α，Φ，U，N，g) is non-decreasing asNincreases. This guarantees the existence of the following limit

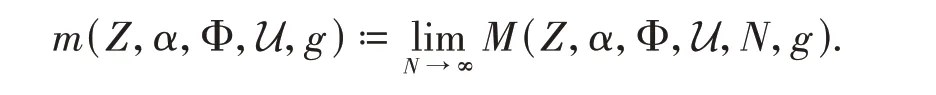
There exists a critical value of the parameterα，which we will denote byPZ(G，Φ，U，g)，wherem(Z，α，Φ，U，g) jumps from ∞to 0，that is，

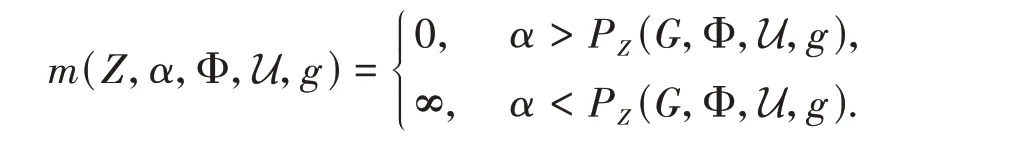
The following theorem discusses the connection between the above definition and the topological pressure of free semigroup actions defined by using open covers.

Theorem 1For any setZ⊂X，the following limit exists and equals to the topological pressure of a free semigroup actionG，that is，

ProofWe use the analogous method as that of［3］. On the one hand，givenw=i1i2…iN∈，for any U ∈Sn+1(U)，we denote the word that corresponds to U bywUsuch that，and corresponds to UgbywUgsuch thatwUg=wU，then we have

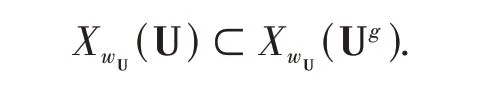
Let

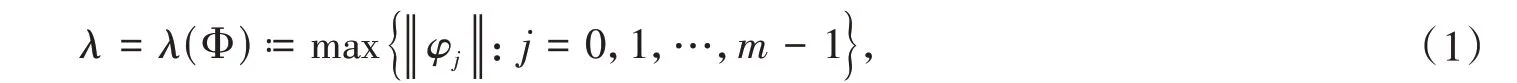
and

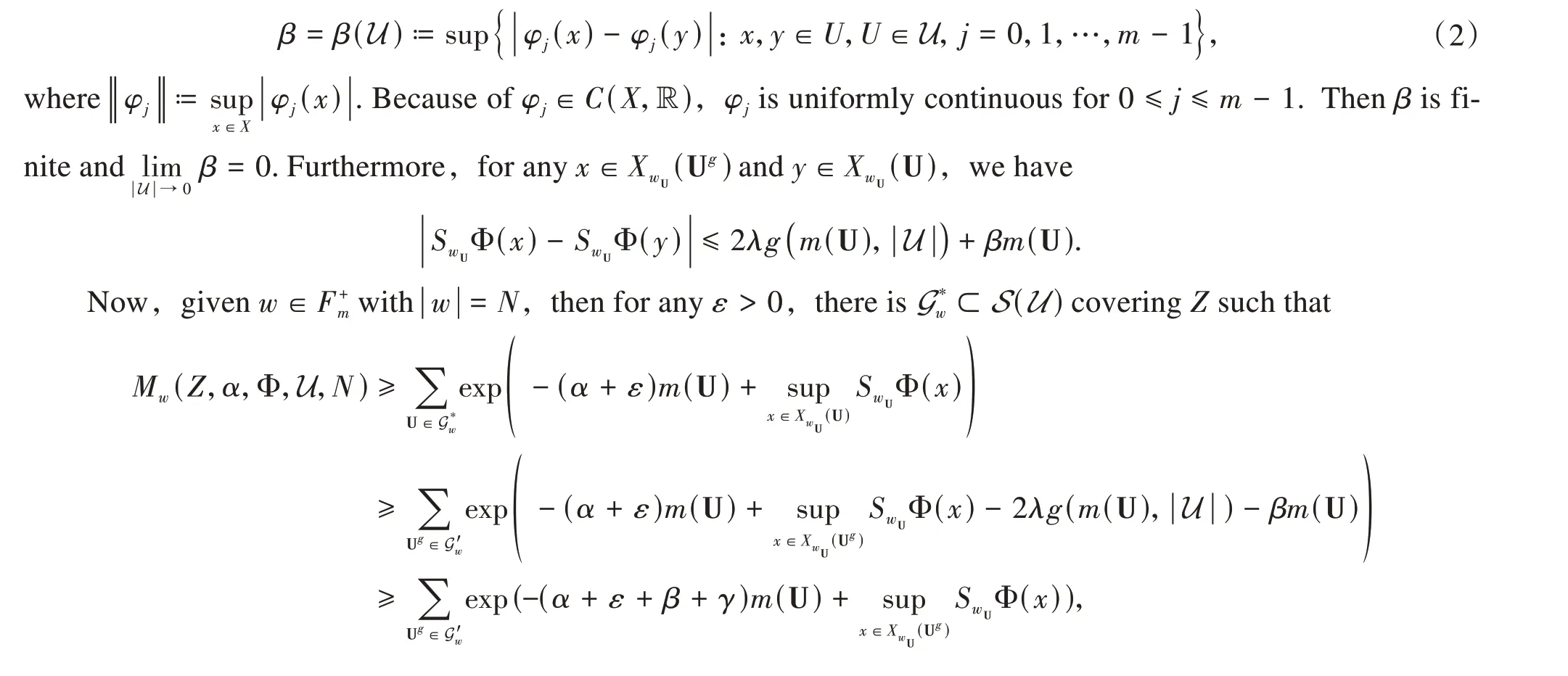
whereG′w={Ug：U ∈，wUg=wU}，γis a function such that

for allm(U) ≥N+ 1 andγ→0 as|U| →0.Moreover，we can get

which implies

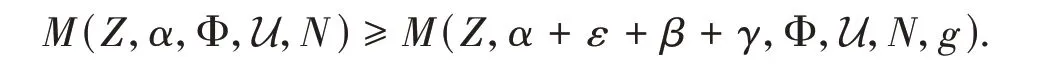
Taking the limitN→∞yields

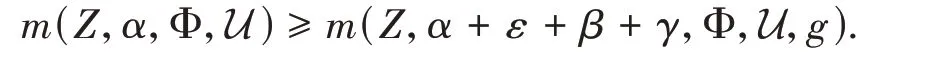
Therefore，

and as|U| →0，that is，β→0，γ→0，we obtain

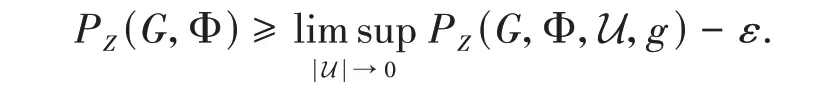
By the arbitrariness ofε，we have

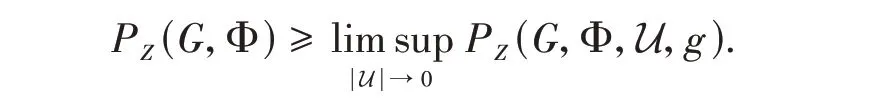
On the other hand，note thatwU=wUg，for any Ug∈(U)，we can find

strings U ∈Sm(U) such that

whereτis the collection of such U.Using Stirling formula，there existsγ1＞0 such that

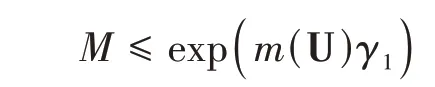
for allm(U) ≥N+ 1，andγ1→0 as |U| →0. Givenw∈with |w| =N，andε＞0，there is⊂S g(U)coveringZsuch that

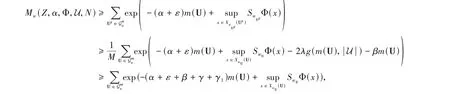
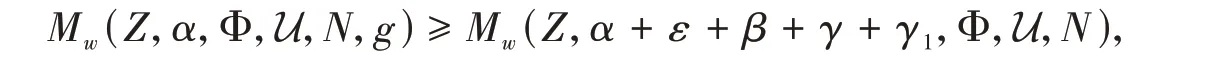
which implies

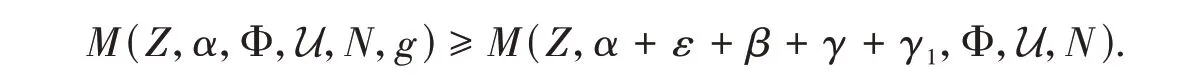
Take the limitN→∞and we get

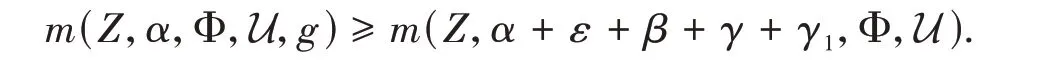
Therefore，

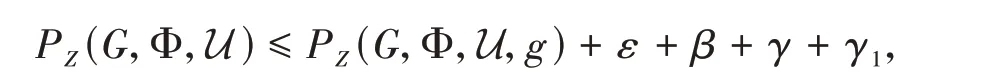
and as ||U →0，that is，β→0，γ→0，γ1→0，we obtain

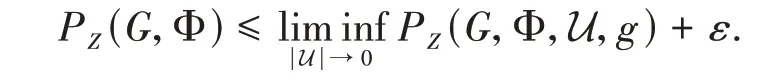
Sinceε＞0 is arbitrary，we have

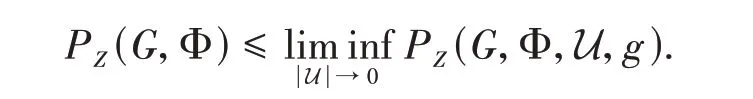
This completes the proof.

The quantityPZ(G，Φ，g) is called the topological pressure of a free semigroupGunder a mistake functiongwith respect to Φ on the setZ.

2.2 Definition of topological pressure of free semigroup actions under a mistake function by using the center of mistake Bowen balls

Now，we introduce a definition of mistake Bowen ballBw(g；x，δ) for a givenw∈F+m.

Fix a numberδ＞0. Givenw∈F+mand a pointx∈X，the mistake Bowen ballBw(g；x，δ) centered atxwith radiusδand length ||

w+ 1 associated to the mistake functiongis given by the following set，i.e.，

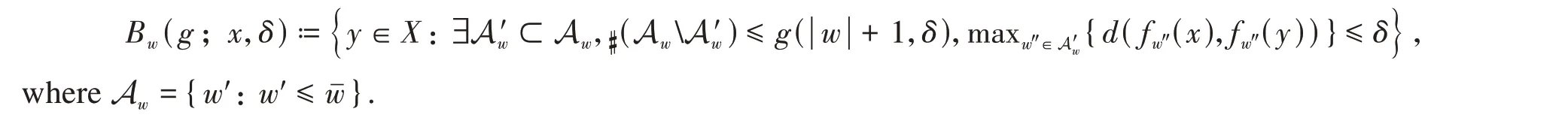
It is obvious that the(w，δ)-Bowen ball is a subset ofBw(g；x，δ).

Now，we describe another approach to redifine the topological pressure of a free semigroupGunder a mistake functiongby the center of mistake Bowen ball.Define the collection of subsets

It is easy to verify that the functionM′(Z，α，Φ，δ，N，g) is non-decreasing asNincreases. This guarantees the existence of the limit

There exists a critical value of the parameterα，which we will denote byP′Z(G，Φ，δ，g)， wherem′(Z，α，Φ，δ，g) jumps from ∞to 0，namely，

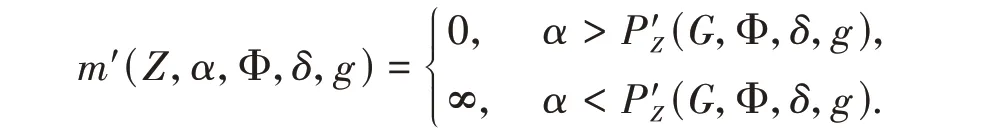
The following theorem proves that the two definitions of topological pressure of free semigroup actions under a mistake function are equivalent.

Theorem 2For any setZ⊂X，the following limit exists and equals toPZ(G，Φ，g) defined by using open covers，that is，

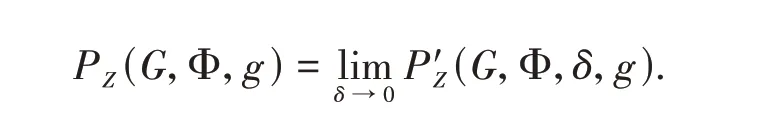
ProofOur proof is adapted from Climenhaga's elegament argument in［11］. On the one hand，givenδ＞0，let

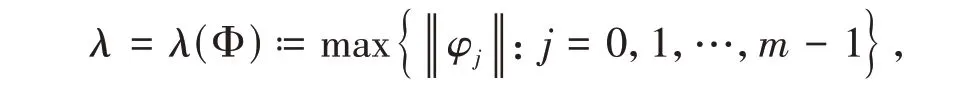
and

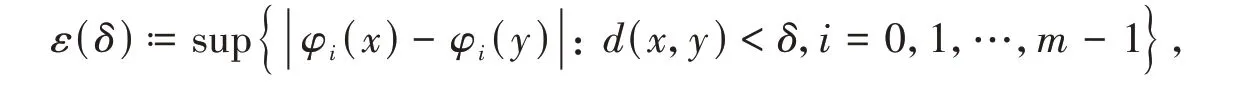
Note thatm(U) =m(Ug′)=|w′ |+ 1，then

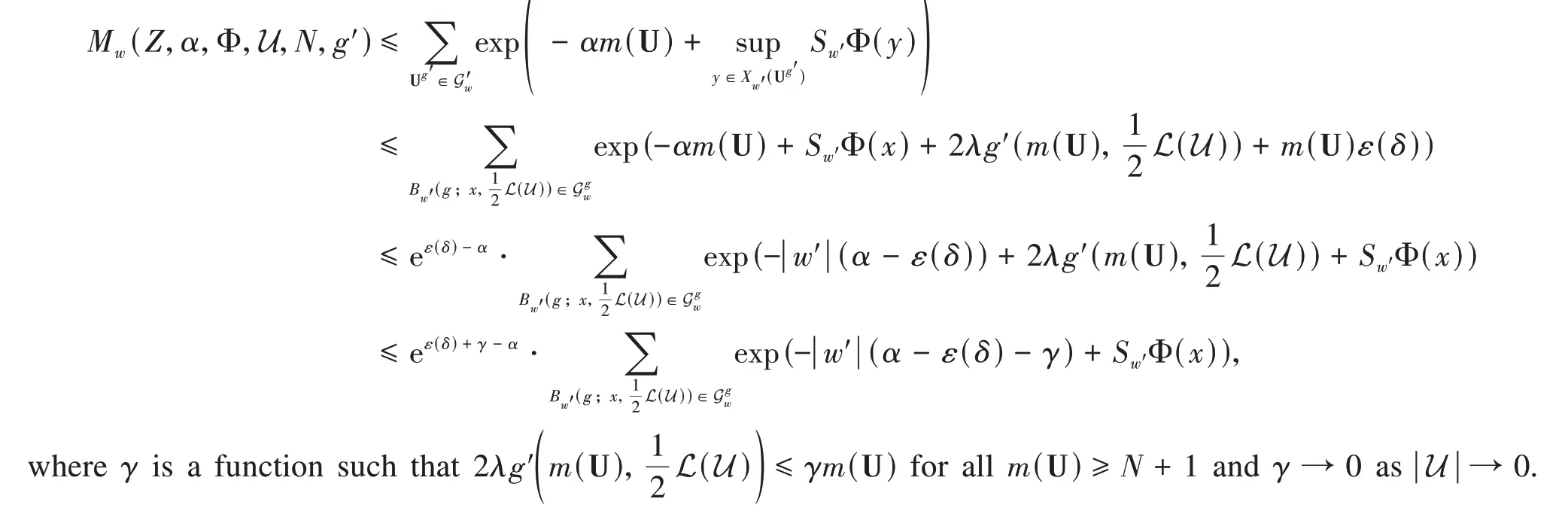
Moreover，we can get

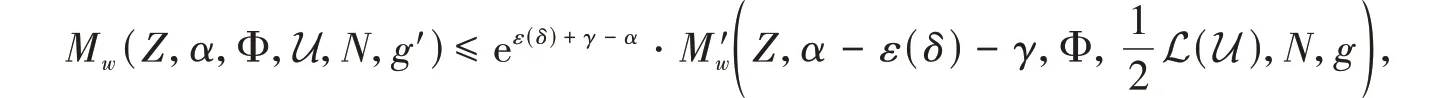
which implies

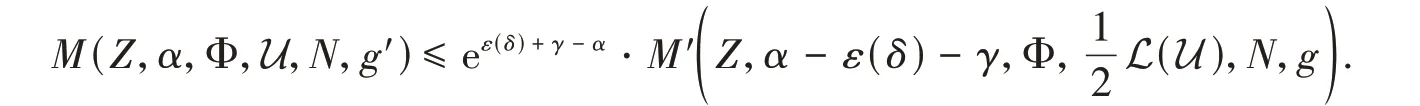
Taking the limitN→∞yields

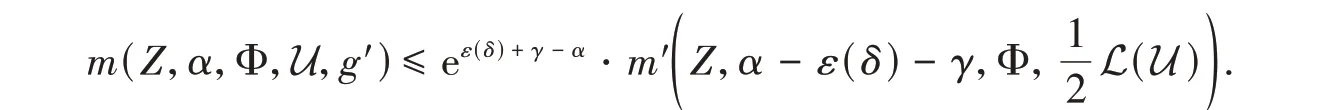
This implies that

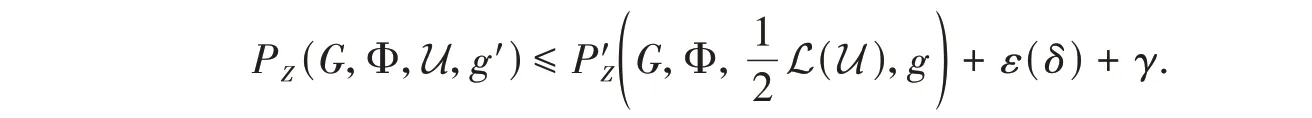
Asδ→0，that is，ε(δ) →0，|U| →0，γ→0，we obtain

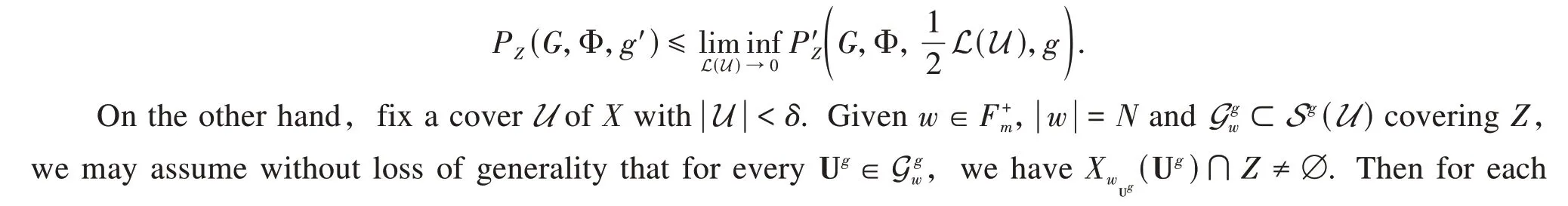
It follows

Hence

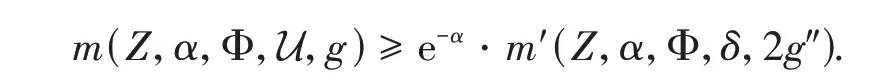
This implies that

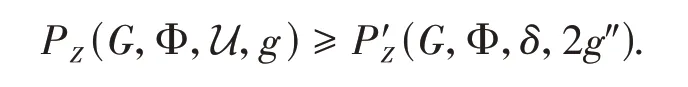
Taking the limit asδ→0 gives

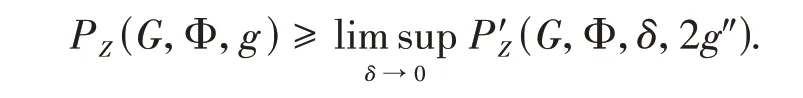
It is obvious thatBw(g″；x，δ) ⊂Bw(2g″；x，δ)，then we obtain

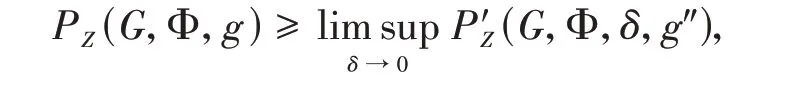
which completes the proof.

2.3 Example

Let(X，d) be a compact metric space，f0，f1，…，fm-1continuous transformations fromXto itself. Similar to the definition of mean metric in［12］，for anyx，y∈X，w∈F+m，we define a mean metric-dwonXas follows：

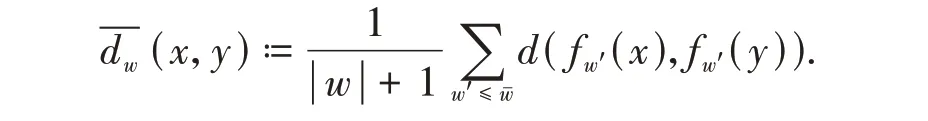
Forx∈Xandδ＞0，let

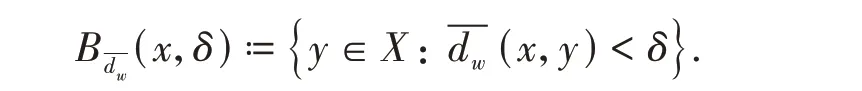
In 2015，Gröger and Jäger［9］gave a definition of topological entropy of the whole system in mean metric by using separated sets，and proved that the topological entropy defined by mean metric is equivalent to the topological entropy defined by Bowen metric. Similar to the process of defining topological pressure of a free semigroupGin Section 1，we can also use the center of(x，δ) to define topological pressure on non-compact subsetZ，denoted by(G，Φ).

Proposition 1For anyZ⊂X，we have

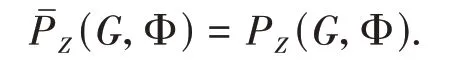
Now，we chooseg(n，ε) =nε. It's clear that this function satisfies the definition of the mistake function.By the following lemma and Theorem 1，it is easy to obtain the above proposition，hence we omit the proof.

Lemma 3For anyx∈X，w∈，andε＞0，we have

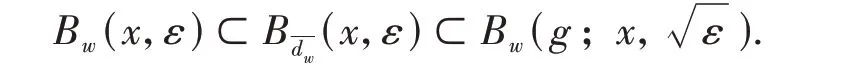
ProofFor anyy∈X，w∈，ifdw(x，y) ＜ε，then(x，y) ＜ε，so we have

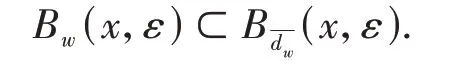
Set

whereAw={w′：w′≤w}.Since

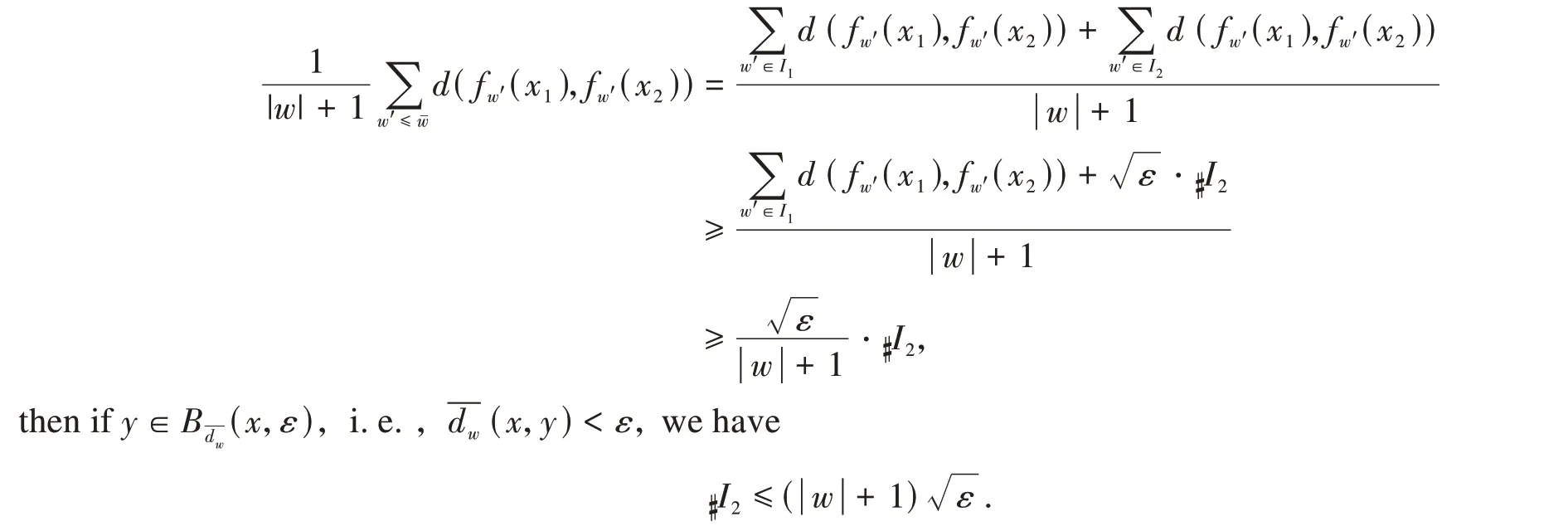
Thus，we obtain

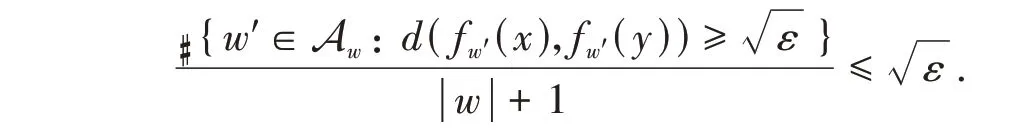
Theny∈Bw(g；x，).Therefore，we have