幂等矩阵线性组合的可逆性及逆的表示

冯福存, 常莉红, 韩惠丽

(宁夏师范学院 数学与计算机科学学院, 宁夏 固原 756000)

0 引言

近年来,国内外很多学者对各种特殊矩阵的组合及组合的相关性质进行了广泛和深入的研究,并得到了一些很好的结果[1-3].幂等矩阵作为一类重要且性质丰富的特殊矩阵，具有广泛的应用,国内外许多从事相关研究的专家发表了一系列文章[4-5].由于密码学、统计学和系统理论中的很多问题都与幂等矩阵的线性组合密切相关,因此很多学者对两个幂等矩阵组合的性质产生了浓厚的兴趣,并对其进行了深入的研究和探索.文献[6]研究了两个幂等矩阵线性组合的可逆性问题,得到两幂等矩阵线性组合可逆的若干充分必要条件.文献[7]给出了在Banach空间中两个幂等算子线性组合的局部性定理.文献[8]讨论了两个幂等矩阵的和、差与线性组合非奇异性之间的一些关系.文献[9]研究了3个互不相同的同阶幂等矩阵,在任意两个可交换的条件下它们线性组合的幂等性和可逆性.通过对它们的研究,使得算子系统结构的内在关系变得更加清晰,也让相关的矩阵理论的课题研究有了坚实的理论基础.

本文在以上文献的基础上,进一步讨论一组幂等矩阵在特定条件下的可逆性问题,讨论任意方阵分解为幂等矩阵线性组合或幂等矩阵与幂零矩阵的线性组合问题,并在此基础上给出任意可逆矩阵分解为一组幂等矩阵线性组合的表示形式.

1 基本概念和记号

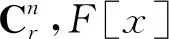
定义 1.1[10]设A是n阶矩阵,如果A2=A,则称A为幂等矩阵.

关于幂等矩阵有如下结论:

结论 1.1[11]幂等矩阵A可对角化,且特征值只能为0或1.

结论 1.2[12]幂等矩阵不一定是对称矩阵.

结论 1.3[12]幂等矩阵A满足r(A)=tr(A).

结论 1.4[11]A是幂等矩阵的充要条件是r(A)+r(I-A)=n成立.

结论 1.5[12]若A是幂等矩阵,则A可逆当且仅当A=I.

2 幂等矩阵线性组合的可逆性

首先给出满足特定条件的一组对称幂等矩阵所具备的性质,然后给出满足特定条件的这组对称幂等矩阵线性组合的可逆性判定.

定理 2.1若A1,A2,…,Am均是n阶对称幂等矩阵,其中r(Ai)=ri,且A1+A2+…+Am=I.则：

1)r1+r2+…+rm=n;

2)Ai+Aj(i≠j)是对称幂等矩阵;

3)AiAj=AjAi=0(i≠j).

2) 令B=Ai+Aj,C=I-B,则B为对称矩阵,且

n=r(I)=r(B+C)≤

r(B)+r(C)=

r(Ai+A

所以

n=r(B)+r(C)=r(B)+r(I-B)，

得B是幂等矩阵,因此,Ai+Aj是对称幂等矩阵.

3) 由Ai+Aj是幂等矩阵,可得

AiAj+AjAi=0,

(1)

(1)式两边分别左乘和右乘Ai，得

AiAj=AjAi=-AiAjAi,

得

AiAj+AjAi=2AiAj=2AjAi=0,

所以

AiAj=AjAi=0,i≠j.

定理 2.2A1,A2,…,Am均是n阶对称幂等矩阵,其中r(Ai)=ri,且A1+A2+…+Am=I.若A=α1A1+α2A2+…+αmAm,则A是对称矩阵,且A可逆的充要条件是αi≠0.

证明A是对称矩阵,显然由定理2.1可知,AiAj=0(i≠j)，故

A(Aix)=αi(Aix).

(2)

由定理2.2的证明过程,考虑其逆过程可得.

定理 2.3A是对称矩阵,若A的特征值为λ1,λ2,…,λm,则存在一组对称幂等矩阵A1,A2,…,Am,使得A=λ1A1+λ2A2+…+λmAm成立.

证明A是对称矩阵,A的特征值为λ1,λ2,…,λm,则存在正交矩阵P使得(3)式成立,

A=PΛPT,

(3)

其中Λ为对角矩阵,对角线上元素由A的特征值λ1,λ2,…,λm构成.

设特征值λi的特征子空间Vλi的维数为ri,(3)式可写为

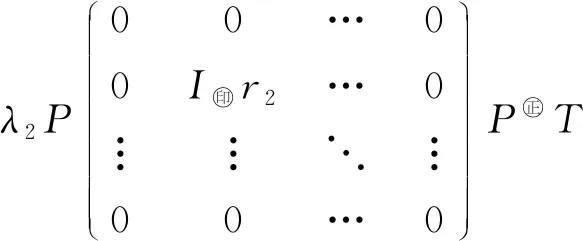
λ=

λ1A1+λ2A2+…+λmAm,

其中

A,

(4)

推论 2.1A是可对角化(非对称)矩阵,若A的特征值为λ1,λ2,…,λm,则存在一组幂等矩阵A1,A2,…,Am,使得A=λ1A1+λ2A2+…+λmAm成立.

在定理2.3中，若A的特征值满足λi≠0(i=1,2,…,m),即A可逆,则有A1+A2+…+Am=I.

定理 2.4A是不可对角化矩阵,若A的特征值为λ1,λ2,…,λm,则存在一组幂等矩阵A1,A2,…,Am和一个幂零矩阵B,使得A=λ1A1+λ2A2+…+λmAm+B成立.

证明A是不可对角化矩阵,设A的特征值为λ1,λ2,…,λm,则存在可逆矩阵P使得

A=PJP-1,

(5)

其中,J=diag(J1,J2,…,Jm)为A的若尔当标准形,Ji是由A的特征值λi构成的若尔当块.

设特征值λi的根子空间V的维数为ri,(5)式可写为

A=

λ

λ1A1+λ2A2+…+λmAm+B,

(6)

满足(Hri)ri=0,令H=(lij)n×n,则

由于A不可对角化,可知lii+1不全为零.取s=max(r1,r2,…,rm),可得Hs=0.Bs=PHsP-1=0.证毕.

3 幂等矩阵线性组合的逆

在前文讨论的基础上,可对应依次给出相应条件的逆矩阵.

证明A是可逆的对称矩阵,则

(A-1)T)*=

故A-1是对称矩阵.

由定理2.3的证明可知

两边取逆,由P是正交矩阵可得

所以

引理 3.1若H是幂零矩阵,f(x)=a1x+a1x2+…+anxn,f(x)∈C[x],则f(H)也是幂零的.

证明因为H是幂零矩阵,不妨设存在正整数t,使得Ht=0,则

f(H)=a1H+a1H2+…+anHn=

(a1I+a1H+…+anHn-1)H,

可得

[f(H)]t=(a1I+a1H+…+anHn-1)tHt=0.

引理 3.2设H=(hij)n×n,其中

hii+1不全为零,则Hn=0,且对任意λ≠0,有

证明

(λI+H)(λI+H)-1=

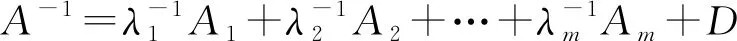
证明A的特征值为λ1,λ2,…,λm,由A是可逆的,可知λi≠0(i=1,2,…,m).

由定理2.4的证明,对(6)式两边取逆，可得

由引理3.2可得

A-1=

其中

gi(H

(-1)

则(7)式可写为

其中Ai如(4)式所示,满足

H=diag(h1(H),h2(H),…,hm(H)),

hi(Hri)=H

(-1)

取s=max(r1,r2,…,rm),由引理3.1,可得Hs=0,Ds=PHsP-1=0.证毕.

致谢宁夏师范学院课程思政示范课程建设(NSSZ2021011)对本文给予了支持，谨致谢意！