区域导航陆基无线电导航系统自动选台优化算法研究

彭旭飞，秦鹏，张萌，张阳康，祖肇梓

1.航空工业西安飞行自动控制研究所，陕西 西安 710065 2.陆军装备部航空军代局，陕西 西安 710065

为了在空中交通中缩小航路间隔，提高空域利用率，同时优化飞行航迹，降低运行成本，国际民航组织（ICAO）提出了基于性能的导航（PBN）的概念[1-2]，并要求按照适航管理体系完成适航验证[3-4]。PBN包含区域导航（RNAV）和所需导航性能（RNP）两类基本导航规范。RNAV是可以使航空器在导航系统信号覆盖范围内，或在机载导航设备的工作能力范围内，或二者组合，沿任意的所需路径飞行的一种导航方式[5-6]。

在RNAV 陆基无线电导航方式中，主要依赖测距机（DME）和甚高频全向信标台（VOR）。由于地面导航台很多，它们使用不同的标识和频率，因此需要选择最合适的陆基导航台进行导航。

为了减轻机组的工作负荷，飞行管理系统（FMS）可以自动选择需要调谐的陆基导航台，再根据测量信息完成位置解算。目前，国外民用飞机（如波音、空客）的FMS已经具备无线电自动调谐和定位的功能[7]。国内学者也进行了相应的研究，提出了DME 台选台算法[8-10]，并将定位精度作为选台算法的考虑因素[11-12]。但是，这些自动选台算法逻辑较为简单，未考虑选台持续性的问题，导致使用过程中会出现导航台频繁切换的问题，影响区域导航的精度和连续性。

本文在分析DME/DME、DME/VOR导航台的信号覆盖范围及实际导航性能的基础上，提出了一种自动选台优化算法，在导航台切换原则中引入有效导航距离和ANP 阈值，并使用北京至上海航路进行仿真试验。结果表明，优化算法可满足区域导航性能要求，同时避免了导航台频繁切换，提高了导航台使用的稳定性。

1 算法设计

1.1 导航台限制条件

DME导航系统由机载测距机和地面测距信标台组成，DME通过询问应答方式来测量飞机到地面导航台的斜距，需要两个及以上的DME 信号，才能确定飞机的位置。DME/DME 定位原理如图1 所示。VOR 导航系统由机载VOR接收机和地面VOR台组成。地面台发送两种信号:一种是固定相位的基准信号；另一种是相位可变的信号。可变信号不断朝各个角度发射相位不同的信号。飞机上的VOR 接收机根据所收到的两种信号的相位差就可以判断飞机处于信号台的哪个角度上，如图2所示。

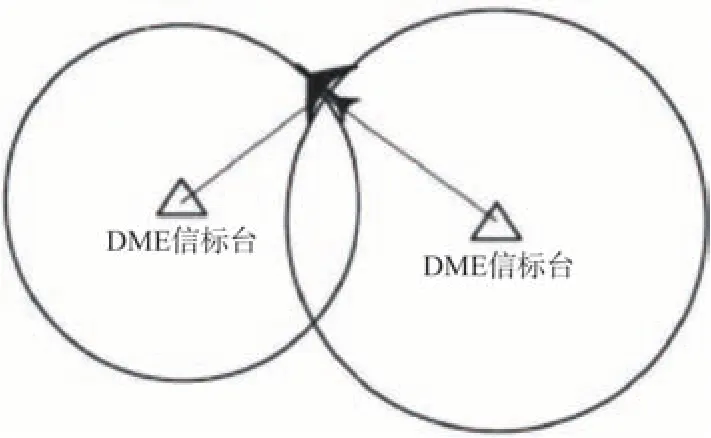
图1 DME/DME定位原理Fig.1 DME/DME positioning principle

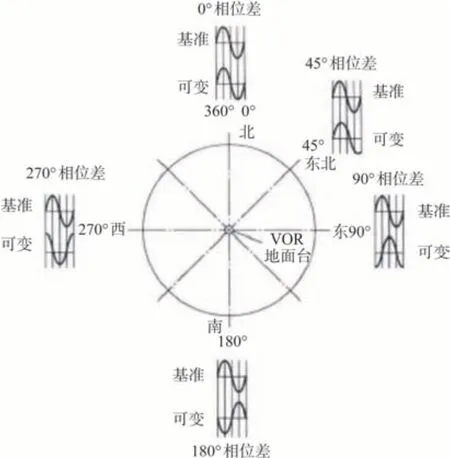
图2 VOR测向原理Fig.2 VOR bearing measuring principle

当信标台同时收发DME 信号时，即构成DME/VOR，也可实现对飞机的定位。DME/VOR定位原理如图3所示。

图3 DME/VOR定位原理Fig.3 DME/VOR positioning principle

由于在选台的过程中，DME/DME方式在定位精度、使用范围等多个方面均优于DME/VOR 方式，所以若飞机具备利用DME/DME 方式的条件，就不会选择DME/VOR 方式。使用无线电导航台时还有多个限制条件。

（1）距离限制条件

根据PBN手册中的规定，导航台到飞机的距离L大于160n mile（1n mile≈1852m）和小于3n mile 时均不可参与基于性能的导航。因此飞机到可用导航台的距离应满足:3n mileL＜160n mile。

（2）VOR台顶角盲区限制条件

导航台的顶空静锥为工作盲区，当飞机处于盲区中时，导航台也不可用，该静锥一般为30°，如图4所示。

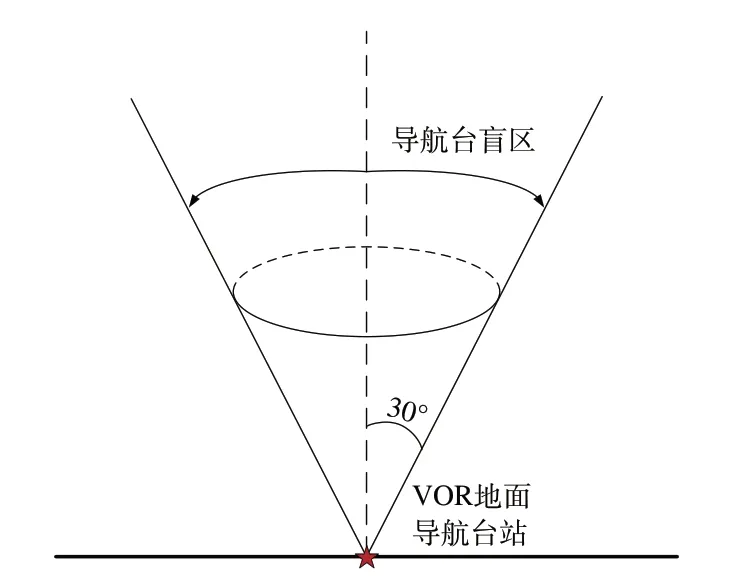
图4 导航台盲区Fig.4 Blind area of navigation station

（3）DME/DME角度限制条件

飞机与两个DME 导航台连线的夹角必须满足30°～150°条件。

以两个DME 台的位置为圆心，以其导航台信号覆盖范围R为半径画圆，这两个圆的交集是飞机可以同时接收两个DME 导航台信号的区域。再考虑飞机与两个DME 导航台连线夹角满足30°～150°的区域:以两个导航台之间的连线为基准形成两个等边三角形，以等边三角形的顶点为圆心，以两个DME导航台之间的距离r为半径画圆。这两个圆的并集与两个DME导航台信号覆盖范围的交集再除去盲区的部分就是满足30°～150°夹角条件的区域，如图5所示。

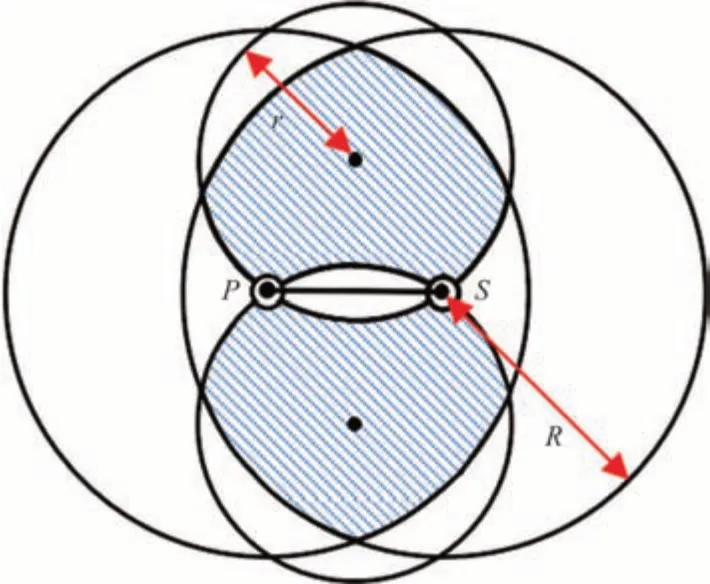
图5 DME/DME有效导航区域Fig.5 DME/DME effective navigation area

1.2 实际导航性能评估

对无线电导航进行实际性能评估，既是RNAV 体系下的导航性能要求，也是导航台选台算法的考虑因素。实际导航性能用ANP 表示，定义了一个误差圆半径，其能使飞机实际飞行位置有至少95%的概率落入该圆内，单位为海里[13]。

（1）VOR系统测量均方差

根据RTCA DO-236B，VOR系统精度的基本表达式是

式中，GS_error 为地面站校准和弯曲误差；D为到VOR 的距离；airborne_error即机载设备误差的标准差，包括接收机噪声。

（2）DME系统测量均方差

DME误差的基本表达式是

式中，GS_error为地面站的时间误差；Air_error为空中误差；K为常数；D为到DME的距离。

（3）ANP计算方法

DME/DME导航模式下，定位误差方差为

式中，φ′为两个DME 地面台与飞机连线之间的夹角；、分别为两个DME 导航台的测量均方差。DME/VOR导航模式下，定位误差方差为

位置估计的水平随机误差服从二维高斯分布，因此1σ误差椭圆的长半轴为σS。对二维高斯分布的概率密度函数积分，可得到其95%不确定度误差圆的半径，即为ANP

式中，K为转换因子，与误差椭圆长短半轴的比例有关，取值范围为1.96～2.45。

1.3 有效导航距离

有效导航距离是指飞机处于某一DME/DME导航台对的有效导航区域内，飞机以当前的方向飞行，DME/DME导航台对可为飞机提供的最长导航距离，直到飞机飞出DME/DME的有效导航区域。导航台选台算法中应考虑有效导航距离因素，当所选的DME 对的有效导航距离过短时，飞机飞行很短的距离就不得不切换其他台站。这样导致导航台跳变问题，在整个航路上有效导航距离都较短，总计切换台站次数过多，即导航台切换过于频繁。

有效导航距离包括三种情况[14]。

（1）飞机在有效导航区域向下一航路点飞行时，与DME/DME 台的夹角逐渐小于30°，从而不满足DME/DME的角度限制条件，如图6所示。

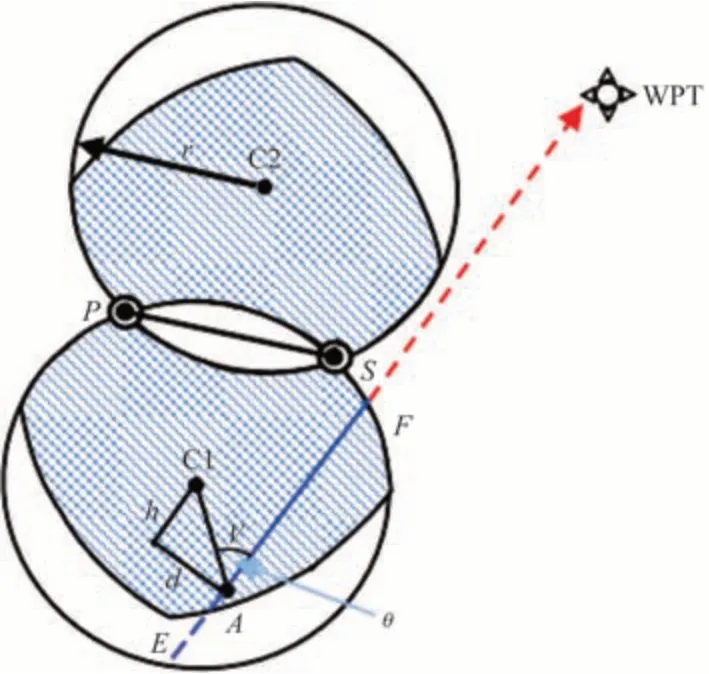
图6 DME/DME有效导航区域情况1Fig.6 The situation of DME/DME effective navigation area 1

（2）飞机在有效导航区域向下一航路点飞行时，航线方向穿过C1和C2源之间的交集。飞机与DME/DME台的夹角会超过150°，不满足DME/DME的角度限制条件，如图7所示。

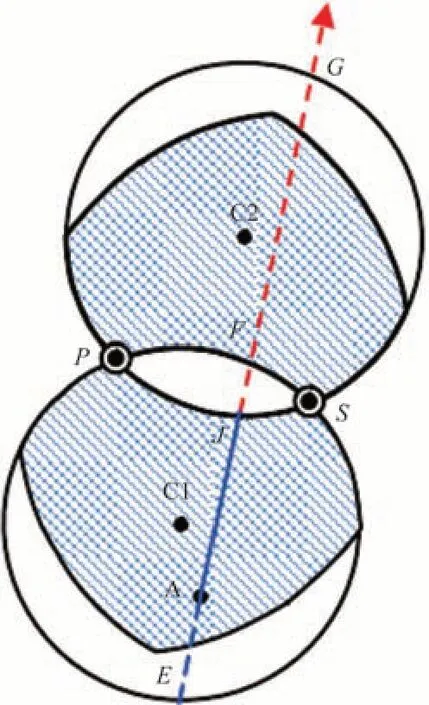
图7 DME/DME有效导航区域情况2Fig.7 The situation of DME/DME effective navigation area 2

（3）飞机在有效导航区域向下一航路点飞行时，航线方向与导航台的覆盖半径相交，使得飞机与导航台之间不满足距离限制条件，如图8所示。

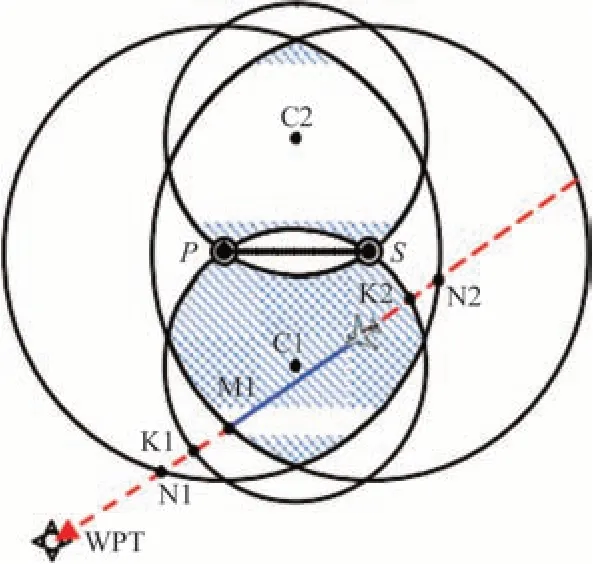
图8 DME/DME有效导航区域情况3Fig.8 The situation of DME/DME effective navigation area 3

1.4 切换原则

传统的无线电自动选台算法为了保证最优导航精度，以ANP 最小作为切换准则，导致所选择的导航台频繁切换，影响定位的连续性。本文对切换原则进行优化时，考虑了有效导航距离和ANP 阈值因素。整个选台算法流程如图9所示。

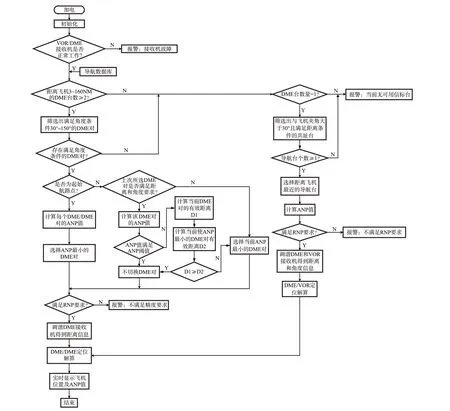
图9 选台算法流程Fig.9 Algorithm flow of navigation station selection

首先经过初始化和工作状态检查后，读取导航数据库中的导航台信息，计算飞机与导航台之间的距离，并筛选出满足3～160n mile限制条件的导航台。当导航台数量不足2时进入DME/VOR分支，当导航台数量≥2时进入DME/DME分支。

在DME/VOR 分支中，排除处于顶角盲区的导航台，优选出距离最近的导航台，并计算ANP。若ANP＜RNP则进行DME/VOR位置解算。在DME/DME分支中，筛选出满足30°～150°角度条件的导航台。当飞机处于起始航路点时按照ANP 最小原则选台，否则在无线电导航设备的主通道中计算当前DME对的ANP和有效导航距离，在无线电导航设备的备用通道中计算使ANP 最小的DME的ANP 和有效导航距离。当ANP 超过ANP 阈值且备选DME 对的有效导航距离大于当前DME 对的有效导航距离时进行导航台切换，否则不切换。完成DME/DME选台后进行位置解算。

在这一选台算法中，对主用DME对和备用DME对的有效导航距离进行判断，可以避免有效导航距离过短而引发导航台频繁切换。此外，可通过设定不同的ANP阈值，调整选台的灵敏度。当ANP阈值较大时，则换台不灵敏，但可能导致定位误差较大；当ANP 阈值较小时，可以保证定位精度，但可能导致选台频繁切换。综上所述，可选飞机和DME/DME台连线的夹角为60°时ANP的值作为换台阈值。

2 仿真计算

以北京首都机场到上海浦东机场航线为例进行仿真计算，对比分析传统选台算法和优化选台算法在导航台使用、换台频度、定位误差、ANP等方面的差异。读取导航数据库中的所有导航台位置，其与飞行轨迹的关系如图10所示。

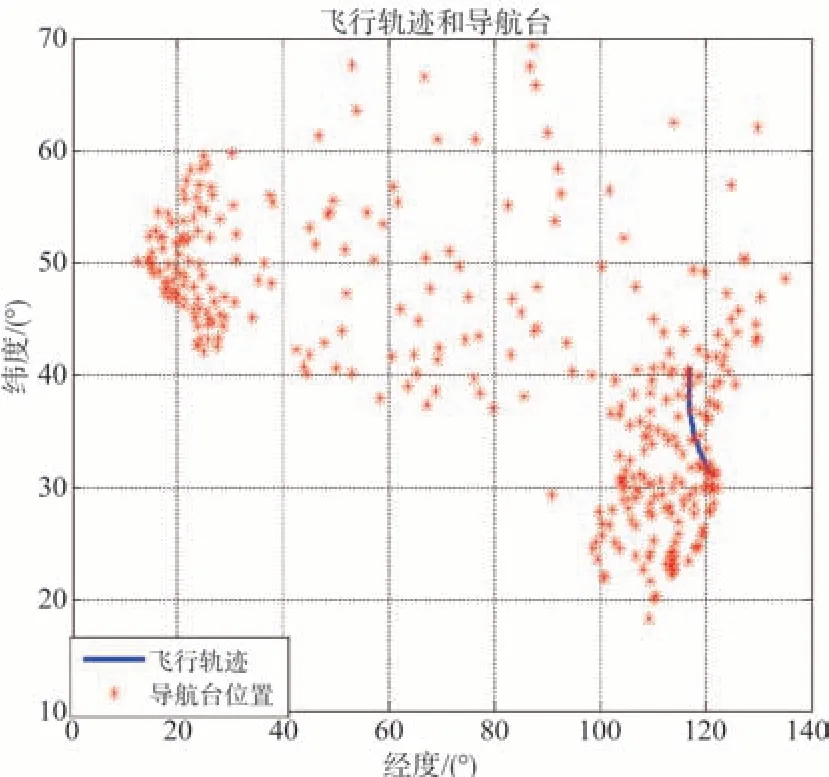
图10 导航台位置和飞行轨迹Fig.10 Navigation station position and flight trajectory

使用传统选台算法和优化选台算法，在整个飞行过程中使用的导航台如图11 和图12 所示。可见部分导航台在传统算法中使用，在优化算法中未使用。说明优化选台算法的切换不如传统算法频繁。

图11 传统选台算法时地面导航台使用情况Fig.11 Usage of ground navigation station with traditional navigation station selection algorithm

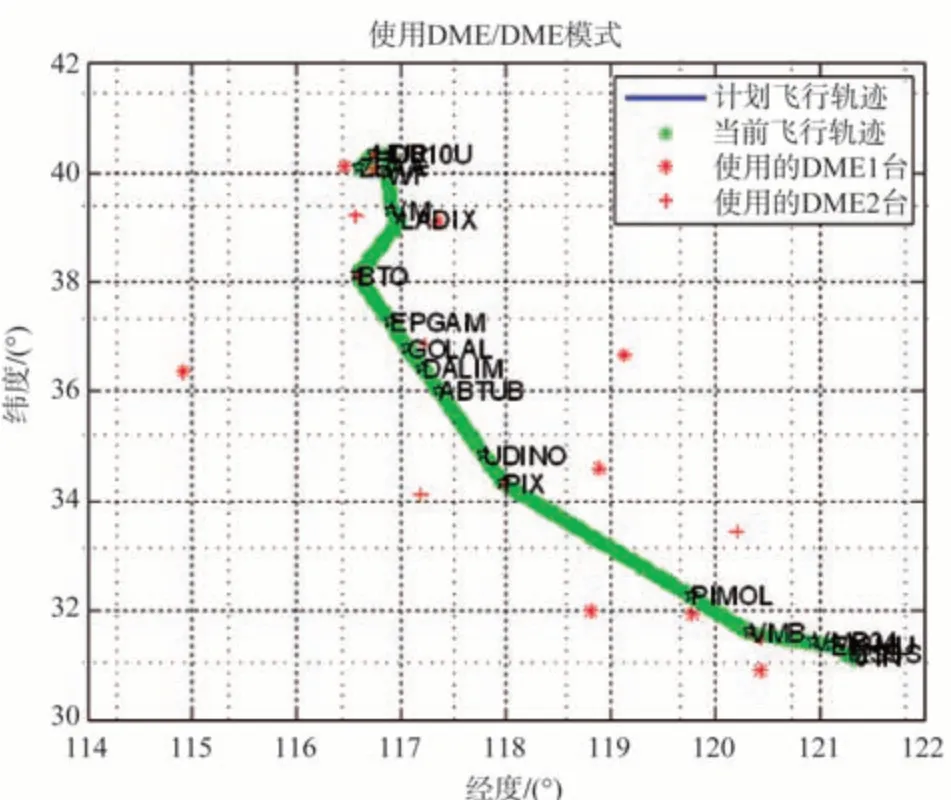
图12 优化选台算法时地面导航台使用情况Fig.12 Usage of ground navigation station with optimized navigation station selection algorithm

使用传统选台算法和优化选台算法的定位误差的ANP如图13和图14所示，两种算法均可以保证ANP不大于RNP（RNP 取4nmile），保证了定位精度。此外，还可以看出定位误差和ANP 的变化趋势一致，存在明显相关性。ANP 跳变是由于导航台的切换。图中红点表示此刻导航台发生了切换，可见优化选台算法相比传统选台算法，换台不频繁。

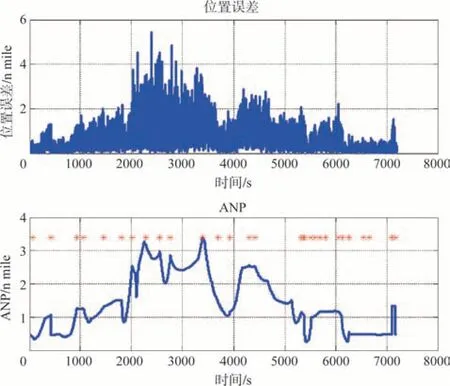
图13 传统选台算法的定位误差、ANP和切换标志Fig.13 Positioning error,ANP and switch flag of traditional navigation station selection algorithm

图14 优化选台算法的定位误差、ANP和切换标志Fig.14 Positioning error,ANP and switch flag of optimized navigation station selection algorithm

在整个航线中，使用传统选台算法和优化选台算法所使用的导航台见表1。

表1 （续）

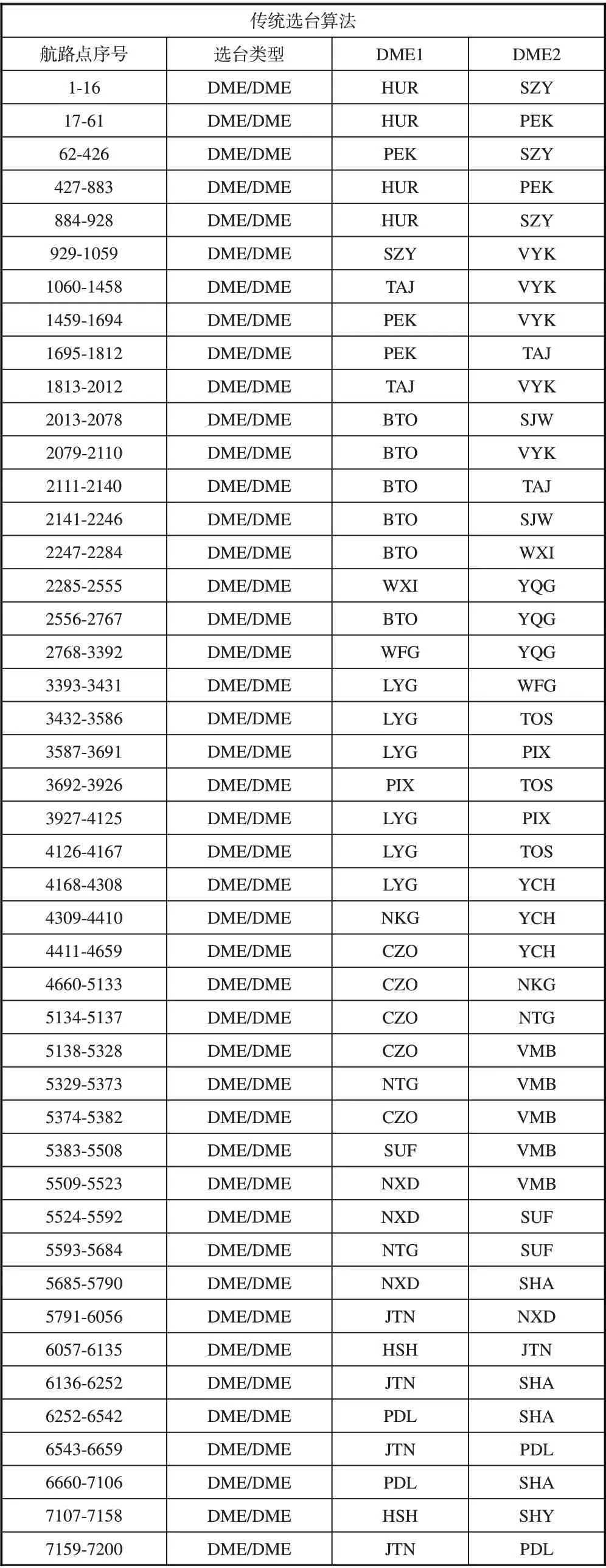
表1 选择的导航台对比Table 1 Comparison of navigation station selection

3 结束语

本文根据RNAV 对导航性能的精度要求，在分析导航台的信号覆盖范围及实际导航性能的基础上，提出了适用于无线电导航的优化选台算法。针对传统选台算法出现的导航台频繁切换问题，综合考虑了主备用DME对有效导航距离、ANP 阈值设定等因素，实现了对切换原则的优化设计。最后使用北京至上海航路进行仿真试验，结果表明优化算法可满足区域导航性能要求，同时避免了导航台频繁切换，提高了导航台使用的稳定性，算法可用有效。