非结构网格热化学非平衡Navier-Stokes方程组求解技术研究

朱海涛，李岩，兰子奇

中国航空研究院数字仿真中心，北京 100012

准确预测高超声速飞行器周围的气动热力学环境是设计、发展和评估新型高超声速飞行器的关键[1]。由于飞行速度很大，在黏性和强激波压缩作用下，气体巨大的动能转化为内能，致使高超声速飞行器所处的气动热力学环境异常苛刻。在地面复现这种高温高焓环境非常困难，进而很难通过风洞试验较为准确地预测高超声速飞行的气动热力学参数，而且成本高昂。高温气体物理化学特性的深入研究和高性能计算技术的快速发展使得先进的计算流体力学方法成为预测高超声速飞行器气动热力学特性不可或缺的重要手段[2]。

数值模拟技术很早便被应用于高超声速流场气动热力学计算。早在20世纪80年代，C.Park等[3]对高温高焓空气的化学反应速率、热力学参数、输运性质等物理、化学特性进行了研究和总结，建立了考虑真实气体效应的三维热化学非平衡Navier-Stokes 方程组。此后，高超声速绕流场数值模拟技术得以快速发展；其中具有代表性的是:M. P.Netterfield 等[4]通过求解二温度热化学非平衡Navier-Stokes 方程组获得了球模型的热化学非平衡数值流场，从中提取了激波位置、驻点温度和组分分布等信息，该算例成为计算高超声速热化学非平衡数值流场的常用对比算例；J.Muylaert 等[5]研究了完全催化边界条件和完全非催化边界条件对高超声速飞行器气动热计算结果的影响，并与风洞试验和飞行试验结果进行对比分析，该算例成为气动热计算的典型对比算例。除此之外，高超声速流动数值模拟的广度不断扩大，开始探索气动热力学环境多物理场耦合数值模拟。例如，B.Hassan等[6]在气/固界面处构造质量、能量平衡的耦合交互面，完成了IRV-2 头部球锥段热化学非平衡流动、非定常材料热响应和烧蚀过程的耦合计算研究，给出了多个弹道点上的表面热流和温度分布。随着火星着落器、星际探测器的兴起，飞行器的速度进一步提高，高温气体内各种非线性物理机制对高超声速飞行器气动热力学环境的影响已无法忽略。描述这些复杂物理机制的新的数学模型也不断被应用于高超声速流场数值计算。例如，Marschall等[7]总结了欧盟航空航天领域使用的多种有限速率催化和化学反应模型，并提出了有限速率表面化学反应的一般框架，用于描述气/固界面热量、能量输运过程。

热化学非平衡Navier-Stokes 方程组数值求解技术也是国内的研究热点。董维中等[8]采用多个振动温度气体模型完成了半球模型和球锥模型绕流的数值模拟，细致研究了气体模型对激波脱落距离、壁面热流、温度分布的影响；高铁锁等[9]通过数值求解热化学非平衡Navier-Stokes方程组获得高温空气组分和温度分布，然后基于辐射传输方程，利用高温气体组分的主要辐射机制，计算分析了辐射加热对返回舱热环境的影响；张子健等[10]提出了一种理论分析和数值模拟相结合的两步渐进法，研究了振动激发过程对二维斜劈气动力/气动热特性的影响规律。董维中等[11]开发了三维热化学非平衡Navier-Stokes 方程组求解软件AEROPH Flow，可以考虑热力学非平衡效应、表面催化效应、烧蚀等因素的影响。邹学峰等[12]对高超声速飞行器热/力/振动/噪声多学科耦合技术的研究进展进行了综述。

高超声速技术的蓬勃发展，促使新型热防护技术、主动流动控制技术以及新型控制舵面等新技术快速应用于工程实践。因此，高超声速飞行器的几何外形越来越复杂，结构形式越来越多样化，基于结构网格的数值模拟技术已不能很好地满足工程实际需求。为此，美国国家航空航天局（NASA）启动了Fundamental Aeronautics Program 项目[13]，发展非结构网格计算技术和基于非结构网格的网格自适应技术即为其中的重要研究内容，并用于发展高可靠性、高效的高超声速热化学非平衡流动数值模拟工具。这个研究领域也引起国内研究者的重视。李鹏等[14]在我国自主开源CFD 软件“风雷”中也开发了非结构网格计算功能，但没有看到详细的计算结果。

本文采用非结构混合网格技术求解三维热化学非平衡Navier-Stokes方程组，与结构网格计算结果进行对比分析，验证了数值求解工具的有效性；同时，针对边界层网格分布和小组分气体计算问题进行了计算研究，并给出了实施建议。

1 热化学非平衡Navier-Stokes方程组

热化学非平衡Navier-Stokes 方程组由经典Navier-Stokes 方程组和描述物理、化学非平衡效应及其耦合效应的模型方程组构成。本文数值计算程序可以计及振动能激发态和离解及置换化学反应，尚无法考虑电子能激发态、光辐射和电离反应。因此，热力学非平衡效应采用二温度模型；化学非平衡效应采用有限速度化学反应模型；二者的耦合效应仅考虑振动温度与离解化学反应之间的相互影响。本文数值求解的热化学非平衡Navier-Stokes方程组为

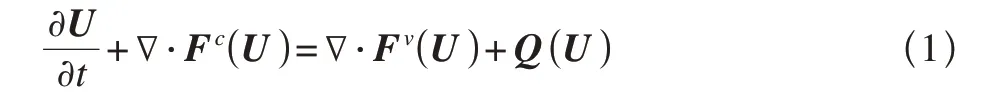
式中

其中，前ns个方程为各个组分的质量守恒方程，其后为三个方向的动量守恒方程，然后是能量守恒方程，最后是振动能方程。U为包含ns个组分的守恒变量:ρi为组分i的密度，ρu,ρE,ρev分别为单位体积混合气体总动量矢量、总能量和总振动能，ρ为混合气体总密度，u,E,ev分别为混合气体质量平均速度矢量和单位质量的总能量、振动能。Fc为对流通量项，I为单位矩阵，p为混合气体压强。Fv为黏性通量项，Ji是组分i的质量扩散通量，遵循Fick扩散定律；τ是黏性应力张量；q是热传导通量，遵循Fourier 热传导定律，由平动—转动温度和振动温度两部分构成；qv是仅由振动温度确定的热传导通量项。Q是源项:ωi是化学反应过程中组分i的生成速率，ωvt是平动—转动态和振动态能量转换过程中振动能生成项，可由Landau-Teller 理论建立不同能量态转换松弛方程是单位质量组分i的振动能量，ωi是由化学反应导致组分i质量变化，进而引起的振动能改变量。这些方程组是不封闭的，需补充以下数理方程。

1.1 热力学方程

热力学方程包括气体状态方程和各能量态内能计算公式。本文采用二温度模型，即平动—转动温度Ttr和振动温度Tv，混合气体的总能量

式中，ei是组分i平动和转动能的和。对分子组分

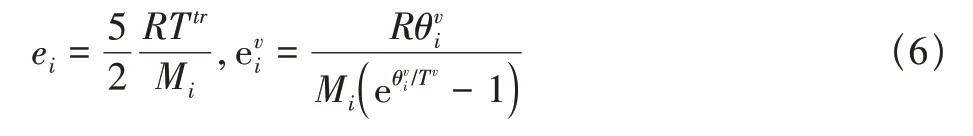
原子组分没有转动和振动能，因此

各组分的分压力仅与平动温度有关，进而混合气体的状态方程为

式中，R为普适气体常数；Mi、分别为组分i的摩尔质量和振动特征温度。

平动—转动模式与振动模式之间存在能量交换。由Landao-Teller理论可知振动能的时间变化率为

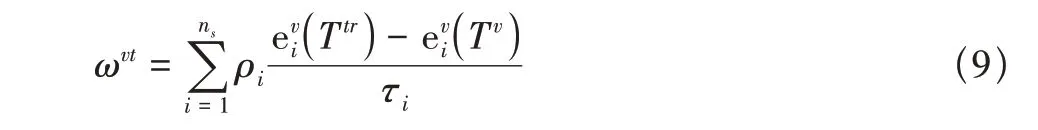
1.2 化学反应模型

对于有nr个化学反应的模型，组分i的生成率为

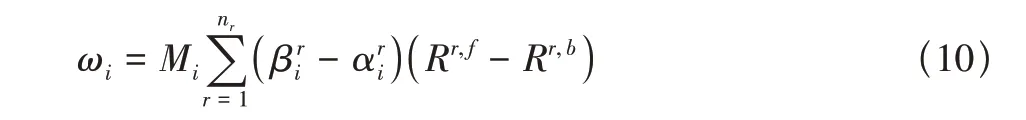
Gupta 给出了高温空气化学反应平衡系数Kr,eq的经验拟合公式，进而可得逆反应的化学反应速率系数为

本文采用5 组分、17 个化学反应的空气化学模型，式（10）、式（11）中用到的常数和经验拟合公式可见参考文献[1]。

1.3 热力学—化学反应非平衡耦合模型

利用化学反应控制温度T建立化学反应非平衡与热力学非平衡之间的耦合关系。5组分空气模型包含置换和离解两类化学反应。采用Park 优先离解模型，置换化学反应的控制温度与平动—转动温度一致，即T=Ttr；离解反应的控制温度由平动—转动温度和振动温度确定，计算公式为T=。

1.4 输运系数

方程组（1）中需要的输运系数有:气体黏度μi、平动—转动导热系数、振动导热系数λvi和质量扩散系数Di。单个组分的黏度和导热系数用Blotter高温气体黏度拟合公式和Eucken经验关系式计算；混合气体黏度和导热系数通过Wilke半经验公式，根据各个组分进行加权平均。扩散系数采用双组元模型计算。具体计算公式可参见参考文献[1]。

式（1）、式（5）、式（8）～式（10）和输运系数计算公式构成封闭的热化学非平衡Navier-Stokes 方程组。引入适当边界条件后构成适定的偏微分方程组初边值问题，即可进行数值求解。本文采用的边界条件包括超声速入口和出口边界条件、对称边界条件、等温壁面边界条件、完全非催化和完全催化边界条件。

2 数值求解方法

对方程组（1）进行空间积分，并采用格点有限元方法离散，在单元控制体上可得如下半离散方程组

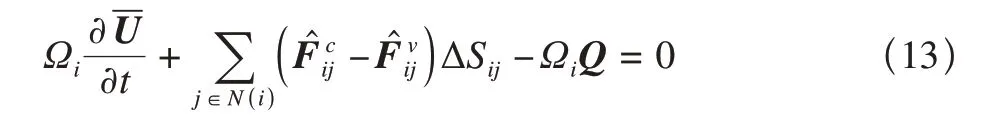
式中，Ωi为网格点i对应的控制体积；N(i)是与点i相邻的网格点集；j是与点i相邻的点，ΔSij是网格边ij对应的对偶网格面积。对流通量项采用AUSM格式计算；黏性通量项首先在各个控制体内采用最小二乘法计算每个网格点上的空间导数值，然后对相邻两点进行平均获得对偶网格面上流动变量、输运系数和相关空间导数值，再计算黏性通量项；源项采用分片常数近似直接在控制内积分。

非平衡效应和各个源项使得离散后线性方程组矩阵条件数很大，数值刚性问题严重。因此在时间离散时，对流通量项和源项进行隐式处理

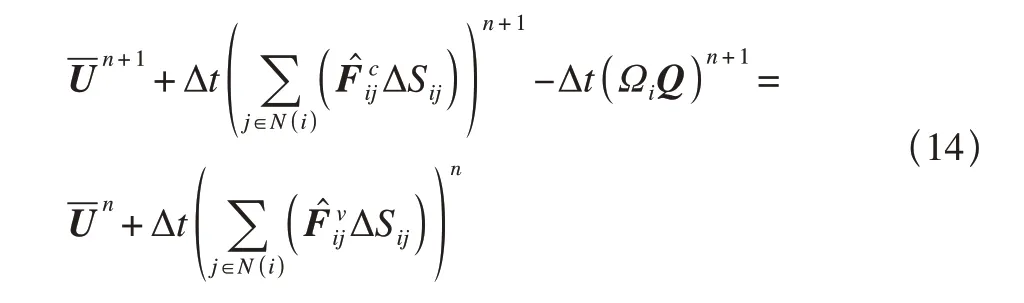
完成空间、时间离散后，采用GMRES算法求解所得线性方程组以更新下一时间步流场信息。

2.1 非结构网格布置

相对于传统亚、跨、超声速流场，高超声速流场具有多组分、高热焓、强激波、强热化学非平衡的特征。基于前者流场特征的非结构混合网格布置规则，能否适用于后者，需进行专门研究。本文以公认结构网格计算结果为基准，对非结构混合网格y+、边界层网格规模、增长率等因素进行细致研究，为高超声速非结构混合网格技术的工程应用奠定基础。

2.2 小组分气体计算

由于高超声速流场热化学非平衡效应，式（13）、式（14）具有很强的数值刚性。不断积累的数值残差对小组分气体计算产生严重不利影响。本文在计算化学反应生成项时，引入元素摩尔数守恒关系式，对一部分组分气体采用式（10）直接计算，其余组分气体由元素摩尔数守恒关系式计算。对5组分空气模型而言，根据元素摩尔数守恒，有

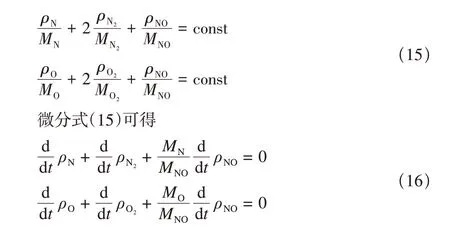
计算过程中，对分子组分N2，O2，NO 采用式（10）直接计算，而原子组分采用式（16）计算，保证各元素摩尔数守恒。与公认的结构网格计算结果对比表明，这种计算方法显著改善了小组分气体的计算准确度。

3 数值结果与分析

本文采用基于非结构混合网格的三维热化学非平衡Navier-Stokes 方程组求解程序计算了半球模型、RAMC II模型高超声速绕流场，并与公认的、采用结构网格的计算结果进行对比分析，还讨论了非结构混合网格边界层网格点布置和小组分气体准确计算问题。

3.1 半球模型

半球模型的半径r= 6.35mm；自由来流速度V∞=5280m/s，静温T∞= 293K，静压p∞= 664Pa；基于球半径的雷诺数Re=14600。壁面采用完全非催化等温边界条件，壁温Tw= 2000K。实际计算中仅取1/4 球面，并采用对称边界条件。

采用4套非结构混合网格，着重考察边界层网格y+、网格增长率γ对数值结果的影响。边界层内棱柱层数目L、边网层网格点数nb和整体计算域网格点数ng等网格参数见表1；其中y+值是驻点附近区域的数值。

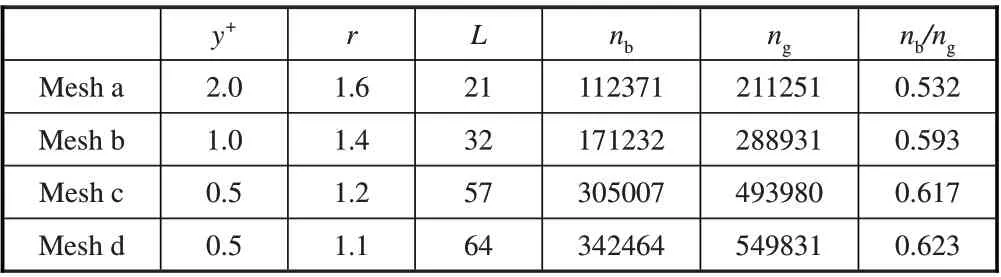
表1 4套非结构混合网格参数Table 1 Main parameters of four unstructured mesh used in present computation

图1给出了物面热流计算结果与公认结构网格计算数据[8]的对比图。由于本文采用全三维计算，图中热流值是每隔15°抽取一条经线，共计13 条经线上热流的平均值。横坐标是经线弧长与球半径的比值。可以看出，第四套网格所得物面热流与公认解基本吻合。由于公认解采用二维轴对称热化学非平衡Navier-Stokes 方程组，无法计及绕纬线方向的流动的影响，因此二者在驻点下游区域存在相对较大的差异。

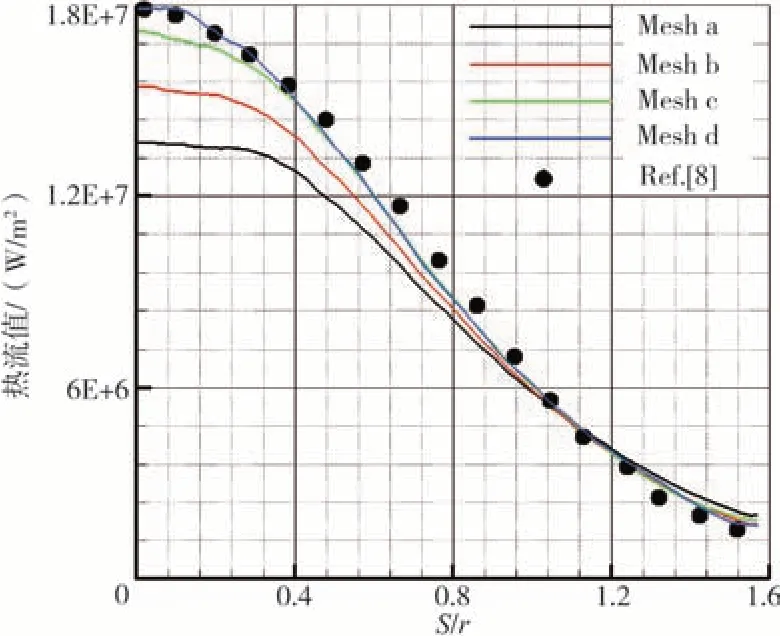
图1 物面热流(w/m2)曲线与公认解[8]对比图Fig.1 Sphere model heat flux(w/m2)of present comparison with reference[8]

图2给出了驻点线上平动—转动温度和振动温度分布与公认结构网格计算数据的对比图。在图2（a）中，第三、第四套网格计算结果与公认结果吻合较好，激波位置也吻合良好。在图2（b）中，非结构网格计算结果与结构网格有较明显的差异:本文最高振动温度出现在激波位置稍下游，与激波比较接近，而结构网格所得最高振动温度与激波有较远的距离。造成差异的原因可能有:（1）振动能控制方程与化学反应、内能模式转化紧密相关，本文采用5组分空气模型，而参考文献[8]采用了7组分或11组分化学模型；（2）本文是全三维计算，而参考文献[8]采用二维轴对称计算，造成流场分布存在差异。

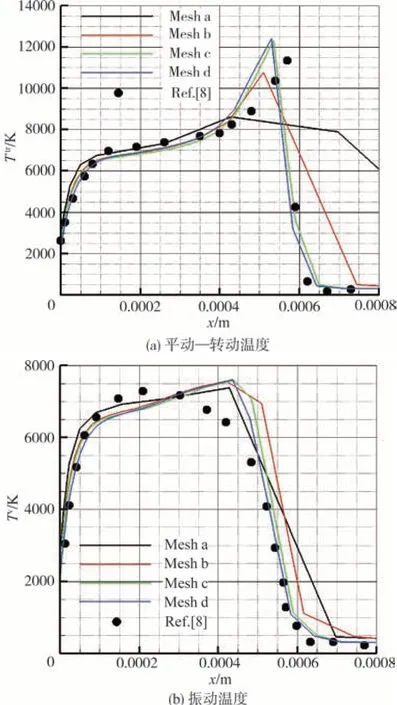
图2 驻点线上平动—转动温度和振动温度分布曲线与公认解[8]对比图Fig.2 Translational-rotational temperature and vibrational temperature in stagnation line of present computation comparison with reference[8]

以参考文献[8]为参考解，可以看出热流对网格分布的要求比流场变量更为苛刻；为了获得准确的热流分布结果，边界层网格y+值应不超过1，边界层增长率应介于1.1～1.2，尽可能使边界层网格点数不低于总网格点数的60%。

3.2 RAMC II模型

RAMC Ⅱ是一个球锥模型，头部球半径为0.1524m，球锥半顶角为9°，轴向长度为1.295m。计算工况为:飞行高度61km；自由来流静压19.2Pa，静温244.3K；飞行马赫数23.9，基于球半径雷诺数19866。物面采用完全非催化等温边界条件，壁温Tw= 1500K。参考文献[15]给出了采用结构网格的详细计算结果。通过与该公认解的对比分析，讨论采用非结构混合网格计算时，两种化学反应源项计算方法对小组分气体数值结果的影响:第一种方法是直接采用式（10）计算各个组分的化学反应生成项；第二种方法是由式（10）和元素摩尔守恒关系式（16）计算各个组分化学反应生成项。

图3给出了驻点线上各组分质量分数分布曲线与公认解的对比结果。其中图3（a）、图3（b）分别给出了直接计算法（方法一）和采用组分摩尔数守恒关系计算法（方法二）所得结果与公认解的对比结果；图3（c）是两种计算方法结果的对比图。可以看出，两种计算方法所得组分质量分数结果与公认解均有一定差异。参考文献[15]采用7 组分空气模型进行二维轴对称计算，因此与本文结果有较明显差异。相对于公认解，采用第二种方法差异更小。由图3（c）可见，两种计算方法对NO组分的影响最为显著。原因是在边界层内混合气体的温度已超过8000K，氧分子已完全离解为氧原子；此时，相对于氮气、氮原子和氧原子，NO组分为小组分气体，对积累的数值误差最为敏感。因此，为保证对小组分气体的准确计算，应采用元素摩尔数守恒关系式计算方法。

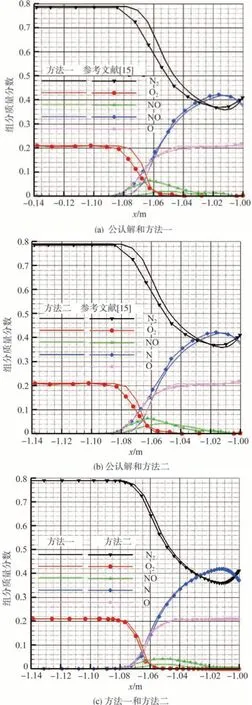
图3 驻点线上各组分质量分数分布曲线与公认解[15]对比图Fig.3 Mass fraction in stagnation line of present computation comparison with reference[15]

4 结论

采用非结构混合网格技术求解三维热化学非平衡Navier-Stokes 方程组，通过与典型算例公认结构网格数值结果进行对比验证，检验了本文数值方法的正确性和有效性。应用本文计算程序，讨论了在采用非结构混合网格进行高超声速流场数值模拟时，边界层网格布置和小组分气体准确计算问题，得到如下结论:

（1）尽管非结构混合网格具有显著的不规则性，且控制方程组离散后系统数值刚性很大，但采用该技术也可以获得与结构网格较一致的流场和热流计算结果。

（2）边界层网格布置对物面热流计算结果影响显著；对二阶格式而言，为保证对物面热流的正确计算，边界层网格y+应小于1（0.5左右），网格增长率应不超过1.4（1.1～1.2）。

（3）小组分气体对数值误差积累较为敏感，为准确计算小组分气体，在化学反应源项计算过程中，应采用元素摩尔数守恒关系式。