坐标系是如何“诞生”的

宋巧巧

我们知道，坐标的意义在于将代数与几何联系起来.然而，坐标系虽然看似简单，但它的形成却是一个十分漫长的过程.

从本质上讲，坐标就是一种位置参考.古代的天文学家们为了确定出天空中星星的位置，自然地用到了某种类似于坐标的方法，即对天空进行网格划分，根据网格位置来确定星体的位置.古希腊天文学家喜帕恰斯（Hipparchus，公元前190-公元前125）用经度和纬度标出天空中点的位置，这就像是给天空画上了网格，利用网格可以标记和快速地找到星星.

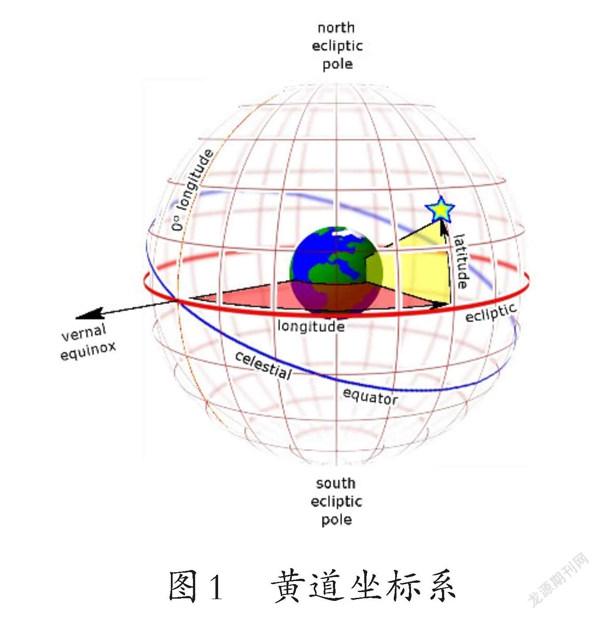
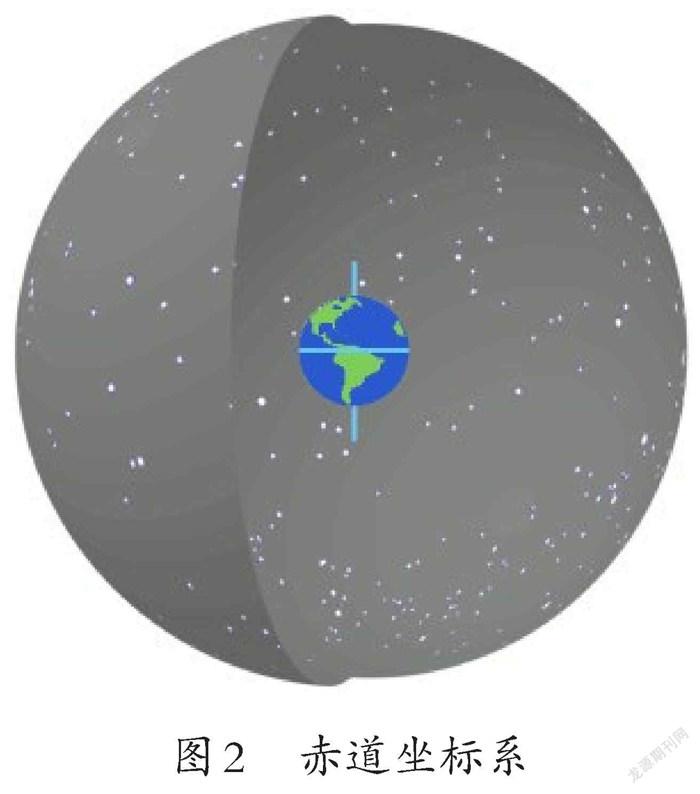
古希腊天文学家和数学家欧多克索斯（EudoxusofCnidus，公元前408-公元前355）曾使用过一种坐标体系标记天空中星体的位置.喜帕恰斯曾评价欧多克索斯在描述恒星位置时采用了恒星的极距（相当于赤道系统的偏角）、赤经（赤道，以赤道为参考面）、经度（黄道，以黄道面为参考）、极经度（混合两种参考）等概念，并给出了两种星空坐标系，如图1（地球绕太阳公转的轨道平面称为黄道，以黄道为参考平面）、图2（假想过天体中心与地球赤道面重合的平面为赤道面，以赤道面为参考平面），但没有提供天体的纬度.

如果在平面上，经度相当于水平线，纬线相当于竖直线，从喜帕恰斯对欧多克索斯的评价可以看出，欧多克索斯的坐标系统，只能确定出星星的高度，并不能准确地定位星星.喜帕恰斯引入纬线，则可以准确地定位星星.后来这种网格坐标被古希腊数学家进行了改进.他们在一个平面底部画出一条水平线，然后在左侧画出一条垂直线（有时是倾斜的），平面内任意点的位置通过该点到水平线和垂直线之间的距离来确定.这样做的意义主要有两点：（1）把可见的网格转变成了隐形的网格，使空间看起来更简洁；（2）由于测量距离的需求，引入了标准的公共设备——尺子，这就向着标准坐标系迈出了重要的一步.

阿波罗尼奥斯（ApolloniusofPerga，约公元前262-公元前190年）在研究坐标系上作出了巨大的贡献.我们现今使用的椭圆、抛物线和双曲线的定义就是由他提供的.在阿波罗尼奥斯的坐标体系中，他将水平线称为“直径”，这里的“直径”就是我们熟知的x轴，“顶点”就是坐标原点，将y轴定义为曲线的切线（参见图3）.

由此我们已经看出阿波罗尼奥斯已经区分出了x轴、y轴、坐标原点，尽管使用了不同的称谓，但在外在形式上，他的坐标轴只是一条直线，并没有方向，也没有负轴，相当于今天笛卡尔坐标系的第一象限.

建立现代坐标系并沟通代数与几何之间的联系的，主要是费马（PierredeFermat，1607-1665）和笛卡尔（RenéDescartes，1596-1650）.

费马在研究阿波罗尼奥斯的《论平面轨迹》后，开始对坐标系进行了深入地研究，用字母来表示几何图形中的点、直线等，如图4所示，设曲线上的一点为J，J的位置随着A、E变化，这个坐标系相当于现在的倾斜坐标系.费马的坐标系利用了韦达的现代表示方法，其特点是没有使用y轴，没有负坐标轴.

费马给出了一条基本原则：只要在最后的方程里出现两个未知量，就可以得到一个轨迹，它可能是一条直线，也可能是一条曲线.如图4中，用x、y表示A、E，它们之间的关系可以用曲线的方程来表示，它的意义在于通过建立坐标系，获得了代数方程，赋予曲线方程以几何意义，无论是对于几何还是代数，这都是巨大的进步.

几何图形比较直观，这引起了笛卡尔的关注.他便产生了把代数应用到几何中的想法，于是创建了笛卡尔坐标系，并主要完成了以下几个方面的工作：

1.利用方程思想解决作图问题.例如，将某个几何问题化归为寻求一个未知长度的线段，设其为x，且满足关系x2=ax+b2，其中a和b为已知长度.由图5和代数运算得出结果x=a2+a24+b2.但笛卡尔只考虑了正根，没有考虑负根.

2.求坐标系中的方程曲线.先选定一条直线，如图6所示，以A点为原点，用x表示AP，用y表示PC.可以看出，笛卡尔与费马绘制曲线的方法，以及坐标的使用方法基本一致.

3.笛卡尔建立了一般方程与曲线的关系，极大地扩展了曲线的范畴.当时古希腊人认为只有用直尺和圆规作出来的曲线才是可靠曲线，但笛卡尔认为只要给定一个含x和y的代数方程，就可以求出它的曲线，而且有些曲线是无法用尺规作出来的.

4.笛卡尔借助坐标研究光学，给出了折射定律.他还解决了一个一般性问题：什么样的曲面作为两种介质的交界面时，从第一种介质内一点发出的光线射到曲面上，折射进入第二种介质恰好汇聚于一点.笛卡尔给出了一种卵形线，如图7（坐标系是后人加的）所示，并给出了曲线的方程.

费马研究坐标的主要目的在于继承希腊人（主要是阿波罗尼奥斯）的思想.但笛卡尔利用坐标提出了更为一般的处理曲线问题的方法，大大超越了费马.也正是由于笛卡尔，人们认识到了坐标系的伟大，并由此诞生了解析几何.

但是，笛卡尔有关坐标的发明，起初并没有引起科学家们的关注.许多科学家认为笛卡尔只是提供了一种几何分析方法，所得到的科学结论，仍没有超越古希腊几何学者所取得的成就.只能说这些科学家只看重知识（几何知识）本身，而没有发现获得这些知识的方法（坐标几何法）的价值.

另一个原因来自于笛卡尔自身.笛卡尔为了体现出自己工作的高深，故意将许多地方写得模糊不清，他曾自称说欧洲的数学家几乎没有一个人能看懂他的著作.还故意删减了一些内容，称他不愿意夺去读者自行加工的乐趣，这或许是一种冠冕堂皇的说法，实际上是担心如果书写得太过于易懂，那些自命不凡的人，将会称笛卡尔所写的东西都是他们已知的东西.

随着对解析几何的推广，坐标系也逐渐被完善，这主要得益于范斯库藤（FransvanSchooten，1615-1660）和沃利斯（JohnWallis，1616-1703）.范斯库藤是荷兰数学家，1632年与笛卡尔相识，并阅读了他尚未出版的《几何》一书，当时觉得难以理解，后来对《几何》做注解，将其翻译成拉丁文于1649年出版，该书后来又多次出现再版，这为笛卡尔坐标系的推广起到了关键作用.更为重要的是，范斯库藤还给出了坐标变换——从一条基线（x轴）到另一条基线变换的代数式，这可能是坐标变换的最早工作成果.

沃利斯是一位英国牧师和数学家，他的主要贡献

在于推动了无穷小微积分的发展.我们在高数中学习到的无穷大的符号∞，就是他发明的，同样他用1∞来表示无穷小.沃利斯在坐标系上的贡献在于他引入了负坐标，将坐标几何的研究由第一象限推广到了四个象限，后来牛顿又用了沃利斯的坐标体系，使得解析几何有了快速的普及.

牛顿在《流数法与无穷级数》一书中还发明了一种新的坐标体系.17-18世纪坐标系是由一个x轴，一个与x轴垂直或成某一角度的y轴构成的.牛顿则采用了固定点和通过该点的直线作坐标轴（类似于极坐标），他还采用了双极坐标，点的位置决定了该点到两个固定点的距离.不过，牛顿的这些成果大约形成于1671年，却到了1736年才出版.而雅各布·伯努利（Ja?kobI.Bernoulli，1654-1705）于1691年在《教师学报》上就发表了有关极坐标的成果，因此通常认为是雅各布首先发明了极坐标.

17世纪中后期，法国数学家拉伊尔（PhilippedeLaHire，1640-1718，）、约翰·伯努利（JohannBernoul?li，1667-1748）、帕朗（AntoineParent，1666-1716）、欧拉（LeonhardPaulEuler，1707-1783）等人，将平面坐标系发展为空间三维坐标系.

坐标系的伟大在于它沟通了几何与代数，首先，几何的概念得以用代数表示，几何的问题也可以通过代数运算求解.反过来，又可以利用几何来解释代数，使代數问题变得形象直观，还可以借助几何去发现那些新的代数结论.拉格朗日曾对这一结合做出过非常高的评价，他说：“只要代数同几何分道扬镳，它们的进展就是缓慢的，它们的应用就十分狭窄.但当它们结合在一起时，相互吸取新鲜的活力，就会以快速的步伐走向完善.”

毫无疑问，将代数与几何联合起来，离不开坐标系，只有在坐标系的框架下，实在物体的运动或变化，才能抽象成为数学模型，问题才得以解决.解析几何学的创立，开启了用代数方法解决几何问题的新时代.在西方数学发展的过程中，几何学似乎一直就是至高无上的.一些代数问题，也都要用几何方法去解决.解析几何的产生，改变了这种传统，在数学思想上可以看作是一次飞跃，代数方程和曲线、曲面联系起来了.