基于优化VMD和SVM的柴油机故障诊断算法

严孝强，张振京，宋业栋※，薛 雷，张 衡

（潍柴动力股份有限公司，山东潍坊 261061）

0 引言

柴油机作为机械运动的主要动力源之一，其工作状态（正常或故障）将直接关系到机械的运行情况，甚至对整个机械系统的安全性与可靠性产生影响［1］，因此有必要对柴油机的故障诊断进行研究。由于振动检测法具有物理特征明显、结构简单、易于检测等特点［2］，一直是研究的热点，特别是近年来随着机器学习方法在各行业中应用的推广，业内专家逐步尝试将振动信号处理和机器学习方法相结合进行柴油机故障诊断的研究。

王建国等［3］将VMD（Variational Mode Decomposition）和奇异值差分谱相结合，进行齿轮早期故障诊断的研究，结果表明，该方法能够准确地提取到齿轮微弱的故障特征信息。王双朋等［4］将VMD算法引入到柴油机气门故障特征提取，结果表明VMD算法在处理振动信号方面具有自适应分解特性，与EMD方法相比较，VMD算法分解出的分量信号与原信号相关性更高，分解效果更好［4］。乔新勇等［5］提出一种基于VMD和多尺度散布熵的柴油机失火故障诊断方法，结果表明VMD算法能够分离出不同频带的模态分量，有效地抑制了噪声干扰。任刚等［6］提出改进自适应遗传算法对VMD算法进行优化，通过迭代寻优得到最优的参数组合，并将该优化VMD算法与SVM（Support Vector Machine）算法相结合应用于柴油机曲轴磨损故障的研究。张超等［7］将EMD能量熵和SVM相结合进行齿轮故障诊断，其性能强于EMD能量熵和BP神经网络［8-9］的结合。蔡艳平等［10］提出了一种基于阈值筛选的VMD振动信号分析方法，并结合SVM算法［11］对同一柴油机8种不同工况下的气门间隙故障进行诊断，结果表明其故障识别率为99.17%。

本文在相关研究的基础上，将优化VMD和SVM相结合，对柴油机曲轴故障、连杆故障和传动惰轮故障进行诊断。

1 VMD分解原理及优化方案

1.1 VMD分解原理

柴油机在运行状态下产生的振动信号较为复杂，是典型的非平稳信号，不宜采用传统的信号处理方式。在经验模态分解（Empirical Mode Decomposition）的基础上，Dragomiretskiy等提出了VMD算法，可将非平稳信号分解为不同时间尺度的平稳信号［12］。VMD算法的目标是将输入信号f分解为K个中心频率为wk的本征模态函数（Intrinsic Mode Function）uk（t），其具体步骤如下。

（1）获取模态的解析信号：

式中：t为时间；δ（t）为冲击函数；u（t）为模态。

（2）将解析信号与其对应预估的中心频率混合，把每个模态的频谱变换到基频带上：

式中：｛wk｝=｛wk，wk，…，wk｝为各模态的中心频率。

（3）计算式（2）中梯度的平方L2范数，估计出各个模态的带宽，建立受约束的变分模型：

（4）引入了二次罚项α和拉格朗日乘子λ，将式（3）转为不受约束的方程。得到增广拉格朗日表达式：

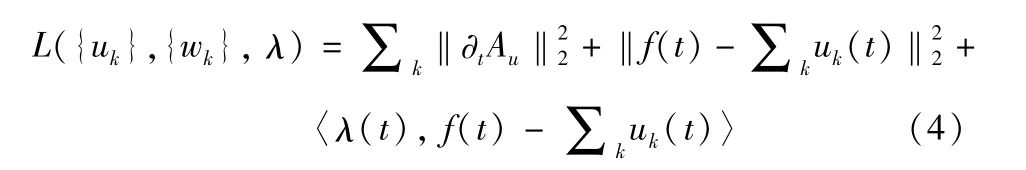
（5）最小值问题则转化为求解增广拉格朗日鞍点问题：

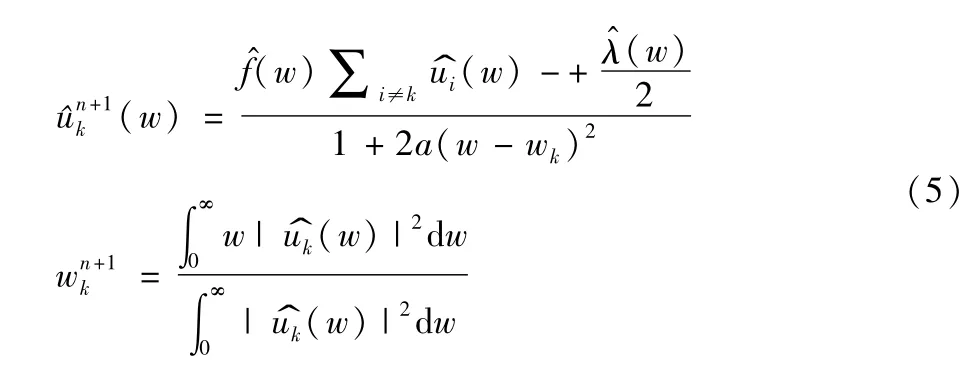
（6）通过换向数乘法依次反复局部优化uk，wk，λ完成求解。即在计算过程中将uk，wk，λ初始化之后进行交替迭代，直至满足迭代停止条件：

迭代完成后，VMD算法输出K个模态分量，即IMF=｛IMF1，IMF2，…，IMFK｝。

1.2 优化VMD

通过以上对VMD分解原理的介绍，VMD分解的效果主要受选取的模态数值的影响，即分解层数K的影响。当K值较小时，由于VMD算法相当于自适应滤波器组，原始信号中一些重要信息将会被过滤，影响后续预测的精度；而当K值较大时，相邻模态分量的中心频率则会相距较近，导致模态重复或产生额外的噪声。分解层数不合理，分解过程中会出现过/欠分解现象，可见分解层数K在VMD中显得尤为重要。文中给出了选取合理分解层数K的优化VMD方案，具体过程如下。

（1）给定K的优化范围。K值最少设置为2，最大为EMD分解层数的2倍。结合经验，在柴油机振动信号处理过程中K值的范围设为［2，12］。

（2）VMD算法分解信号。在选定的K值范围内依次对信号进行分解。

（3）获取有效本征模态函数和数量。假设各IMF与原始信号的相关系数为C，当C大于给定的阈值时则认为该本征模态为有效本征模态函数（Effective Intrinsic Mode Function，简称EIMF），并对EIMF数量进行计次（EIMF-N）［12］。

（4）确定最优K值。统计式（3）中各K值对应的EIMFN，将出现频次最高EIMF-N视为是稳定的K值，并选取最小的K值为最优的K值［13-14］。

（5）使用式（4）中确定的最优K值，对信号进行VMD分解，并且输出EIMF。

1.3 优化VMD验证

为验证优化VMD算法的有效性，设计模拟信号并用优化VMD算法进行处理，得到最优K值和EIMF。模拟信号如下：

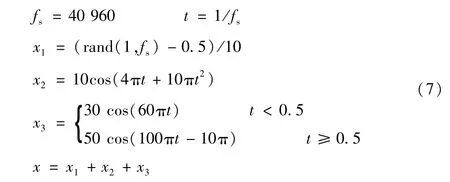
式中：fs为采样频率；x1为模拟噪声；x为模拟信号。

根据上式，绘制模拟信号的时域图，如图1所示。图中，左上为信号x2；右上为t＜0.5时的信号x3；左下为t≥0.5时的信号x3；右下为合成信号x。

图1 模拟信号示意图

采用1.2节中优化VMD方案处理模拟信号x，将相关系数阈值设为0.2，统计各K值对应的EIMF-N值，结果如表1所示。由表可知，在分解层数K=［3，8］内，EIMF-N均为3，故设置分解层数为3，对模拟信号进行分解，并绘制各IMF图，如图2所示。

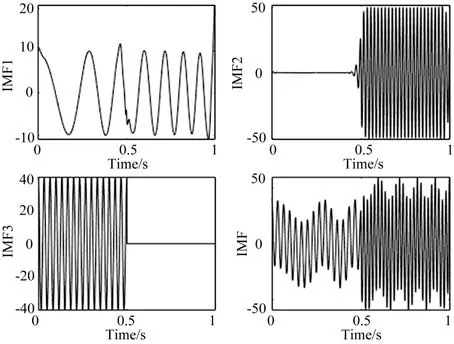
图2 信号VMD3层分解示意图

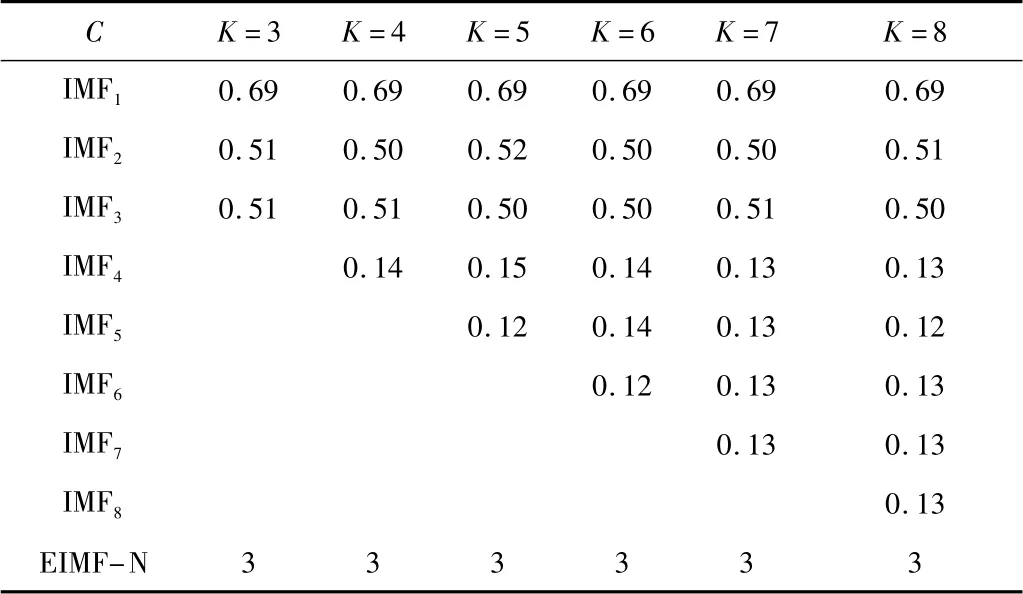
表1 原始信号与IMF的相关系数

通过对比图1和图2，对原始信号进行3层VMD分解后，各IMF均能与模拟信号中各成分相对应。其中，图2中左上为IMF1对应原始信号中的x2；右上为IMF2对应原始信号中t＜0.5时的x3；左下为IMF3对应原始信号中t≥0.5时的x3；右下为IMF对应模拟信号x。

综上证明，该优化VMD算法能够筛选出合理的分解数，解决了VMD算法分解层数难以确定的问题。本文将采用该优化VMD算法处理柴油机的振动信号。

2 故障诊断

2.1 故障诊断流程

本文将振动信号处理和机器学习相结合进行柴油机的故障诊断，其流程如图3所示。

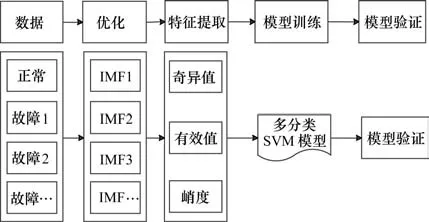
图3 故障诊断流程图

首先，将数据按照实际情况，分为正常、故障1、故障2等；然后，利用上文给出的优化VMD算法对数据进行处理；然后，提取IMF矩阵的奇异值、原始信号的有效值和峭度作为特征向量；最后，将特征向量导入设计好的多分类SVM模型进行训练，并得到分类模型。后续即可利用该分类模型进行故障诊断。

2.2 特征提取

（1）奇异值是矩阵的固有特征，其具有比较好的稳定性，即当矩阵的元素发生小的变动时，矩阵的奇异值变化很小［15］，提取IMF矩阵的奇异值（Singular Value Decompositon，简称SVD）作为特征之一。

（2）有效值是表征整体振动幅值大小的量，提取原始信号中的有效值作为特征之一。其计算公式如下：

式中：x为信号；N为数据点的个数。

（3）峭度能够表征振动幅值概率密度的陡峭程度，提取原始信号中的峭度作为特征之一。其计算公式如下：

（4）构造特征向量。将以上提取的特征构造成特征向量，其计算公式如下：

2.3 多分类SVM模型设计

多分类SVM模型中各参数设置如表2所示。本文数据有正常、曲轴故障、连杆故障和惰轮故障共4类。

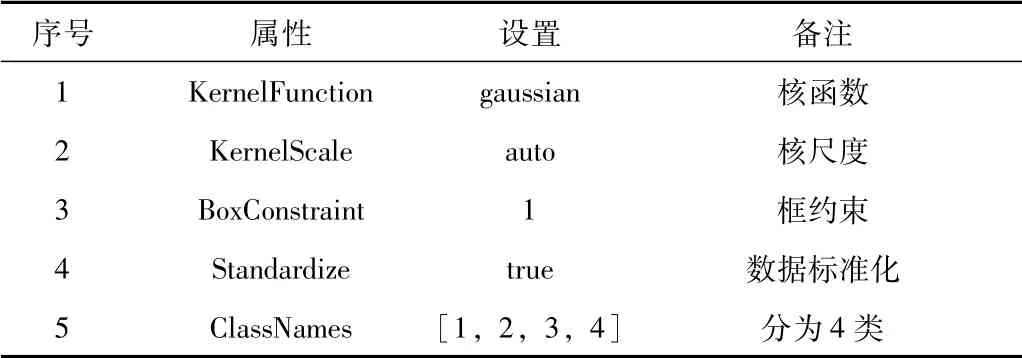
表2 多分类SVM参数设置

3 实验验证

3.1 数据采集

利用某台架某柴油发动机实测数据验证该算法的有效性。采集若干正常、曲轴故障、连杆故障和惰轮故障的数据，数据详细介绍如表3所示。

表3 实验数据介绍

3.2 优化VMD处理

随机选取一组曲轴故障（BF）、曲轴正常（BN）、惰轮故障（GF）、惰轮正常（GN）、连杆故障（RF）和连杆正常（RN），将以上数据集记为D，D=｛BF，BN，GF，GN，RF，RN｝。用优化VMD算法处理数据集D，相关系数阈值设置为0.3，统计分解层数K，结果如表4所示。

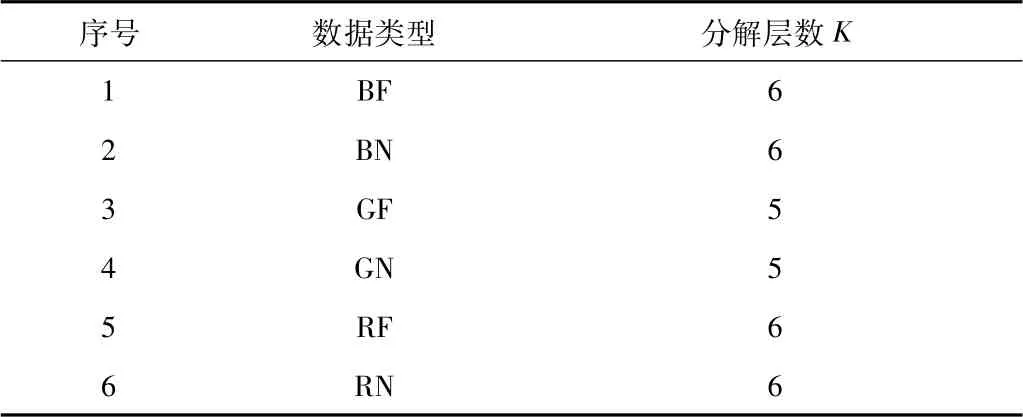
表4 VMD分解层数统计表

按表4确定的分解层数，对BF和BN数据进行6层VMD分解得到各IMF，并绘制其时域图，如图4所示。

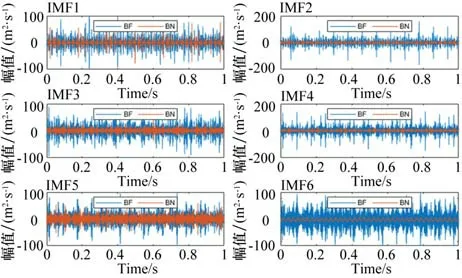
图4 IMF时域示意图

将各IMF进行傅里叶变换，并绘制其频域图，如图5所示。

通过观察图4和图5可以发现，BF和BN数据经过VMD分解后，各IMF在时域幅值存在明显的差异，在频域上也存在明显的差异。

3.3 特征提取

提取数据集D中振动信号的特征值，其结果如表5所示。由表可知，6组数据特征值存在差异性，本文将采用多分类SVM模型处理训练样本数据，得到分类模型。

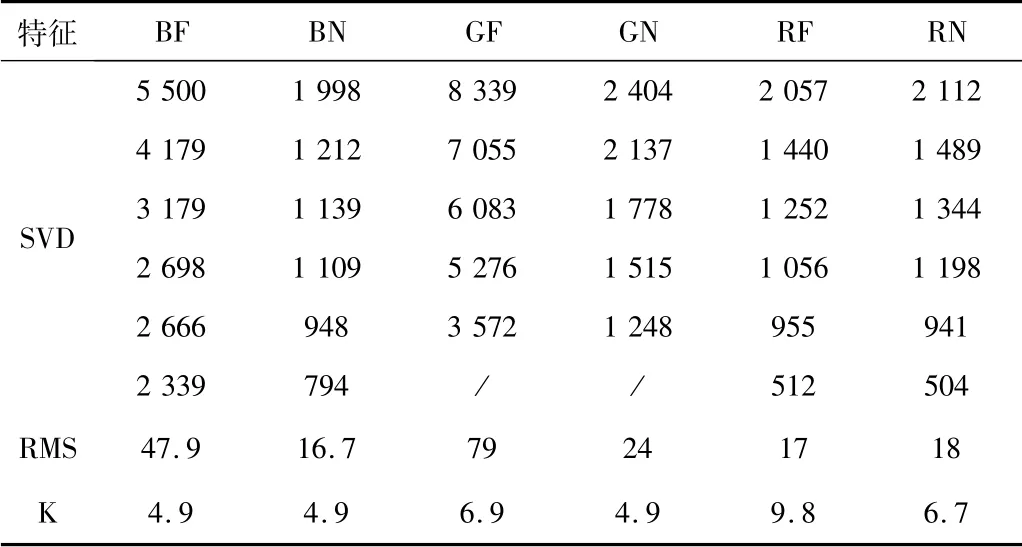
表5 特征值统计表

3.4 分类模型训练及验证

（1）分类模型训练6所示

将。样 本数据按照8∶2随机分为训练数据和测试数据，如表

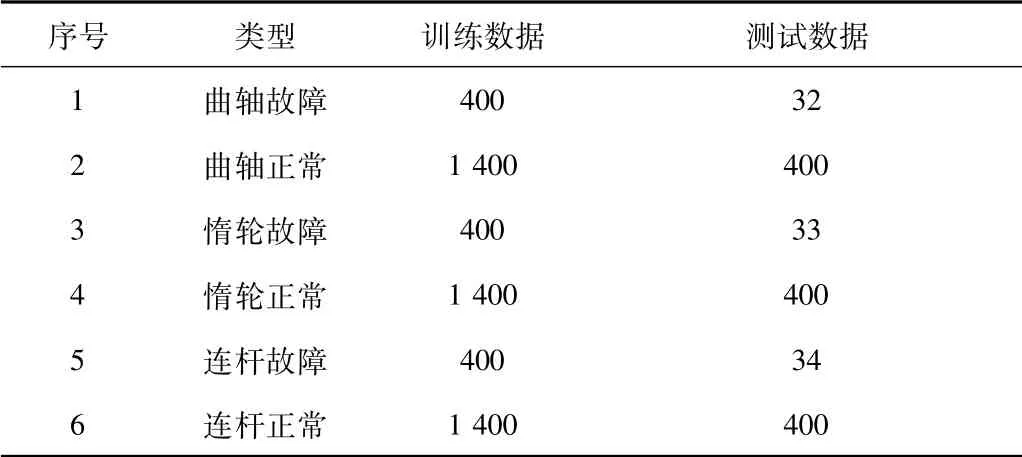
表6 数据分类表

按照图3的流程处理样本数据；按照表4设置VMD分解；特征提取过程中为保证维度一致，惰轮SVD结果需要增加一维并填充为0；按照表2设置多分类模型参数，将正常数据标记为1、曲轴故障标记为2、惰轮故障标记为3、连杆故障标记为4。采用10折交叉验证法评估分类模型，其值为0.006 7，证明该分类模型的误分率较低。

（2）验证

利用测试数据验证该故障诊断算法，绘制诊断结果混淆矩阵，如图6所示。

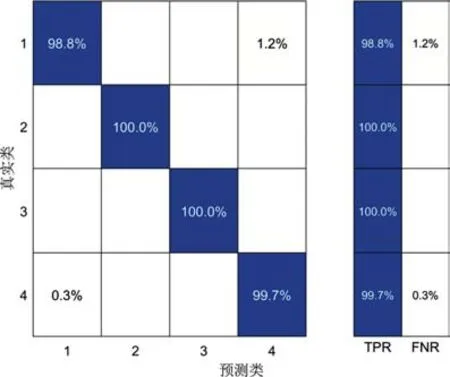
图6 故障诊断结果混淆矩阵示意图

图6纵轴表示真实类、横轴表示故障诊断结果类或预测类；TPR表示正类预测正确的百分比、FNR表示反类预测错误的百分比。由图可知，第1类诊断正确率为98.8%，诊断错误率为1.2%；第2类和第3类诊断正确率均为100%；第4类诊断正确率均为99.7%，诊断错误率为0.3%。综上，该算法的故障诊断正确率为98%以上。

4 结束语

本文将振动信号处理与机器学习相结合用于柴油机故障诊断的研究中，并以台架实测数据验证了该算法的有效性。在振动信号处理过程中，文中给出了优化VMD算法的方案，给出了确定最优分解层数的方法，解决了分解层数对分解结果产生影响的问题；在特征提取方面，提取IMF矩阵奇异值（6维），原始信号有效值和峭度共计3类特征，特征向量维度为8维，为保证特征向量维度的一致性，通过在相应位置增加维度并补0的方法处理维度小于8的特征向量；在分类模型的选择上，本文采用多分类SVM模型；实测数据验证结果表明，该算法的故障诊断正确率为98%以上，证明了该算法的有效性。