基于频域稀疏采样的离轴压缩全息相位重建

蒙彬钧，刘丙才，杨栋，王红军，朱学亮，，钱晓彤，牛瑞，田爱玲，

（1 西安工业大学 兵器科学与技术学院，西安 710021）（2 陕西省薄膜技术与光学检测重点实验室，西安 710021）（3 中检西部检测有限公司，西安 710032）

0 引言

数字全息术［1］通过衍射理论的数值计算来获取物光波的复振幅，相比传统光学全息，其采用光敏电子器件记录下全息干涉条纹，避免了对记录介质进行复杂的光化学处理。通过单帧图像的采集快速恢复物体的三维形貌，具有非接触、实时动态、无损检测的特点［2］。然而，对不同结构的微光学元件进行全息显微测量时，不同纵向深度层面会受到背景信息的干扰，使得全息三维光场中的相位测量精度不高。因此，在探索数字全息波前重建过程中，提高相位重建质量方法的研究具有重要意义。

压缩感知理论［3-4］作为一种新的信号表示与处理的理论，在其理论框架下对稀疏或可压缩的信号，利用测量矩阵将高维信号投影到一个低维空间进行观测，通过求解目标函数极值的方式，从少量观测值中实现原始信号的稀疏精确重构，特别是在高维图像信号的稀疏表示与重建方面拥有广阔的发展前景。压缩感知与全息技术之间的关联性表现在全息记录系统为菲涅耳衍射区域时，测量基相当于傅里叶测量矩阵［5］，CCD记录全息干涉图的过程可以等同压缩编码测量，将包含相位的物光波信息压缩成一幅全息图。BRADY D J等将压缩感知理论与Gabor全息术相结合，提出了压缩感知数字全息成像技术［6］。理论上证明了全息衍射编码满足压缩感知成像中的“非相干”编码的要求，实现三维空间中两个距离较远的蒲公英种子形貌的分层重建，此后，将其用于毫米波压缩感知全息成像［7-8］，同样得到了很好的恢复效果。RIVENSON Y等将压缩感知全息技术用于显微成像领域［9］，利用目标在小波变换域的稀疏特性，大幅降低了成像系统所需测量值数量。与此同时，国内各大高校在压缩全息技术方面也展开了相应的研究，从同轴全息、相移全息、离轴全息、非相干全息等多种全息的压缩感知重建［10-13］，扩展到多层切片物体的层析重建中［14-15］；在同轴全息的重建中能有效消除孪生像的干扰，充分利用探测器的空间带宽积；在三维多层样本的重建中，能有效抑制离焦面信息的干扰，实现不同纵向深度的层析重建。然而，压缩全息在成像方面的应用更多集中于物体的强度恢复，却鲜有对位相型算法的分析研究，现实中没有单纯的强度型物体，即使强度型透明物体都携有一定量深度位相信息。对不同结构的微光学元件进行数字全息显微测量时，由于物体具有连续或者不连续的相位特征，导致传统数字全息再现算法在三维重建中无法精确测量微光学元件的波前相位。

针对上述分析，本文将压缩全息技术应用到离轴全息的波前相位检测中。基于传统数字全息再现算法的重建过程，利用压缩感知理论对傅里叶域内的全息图频谱信息进行随机稀疏采样，并在小波变换域内实现待测物光波有效频谱信息的稀疏恢复；再经过傅里叶逆变换将频域转化到空域，得到重建物光波的复振幅分布，并进一步讨论了采样数与重建图像焦深的关系；针对连续和不连续相位物体展开实验研究，比较了传统衍射再现算法与基于压缩感知的数值重建算法的相位重建结果，分别从相位图重建质量及三维重建精度两个方面分析，得到了比传统衍射重建更高质量的相位重建结果，实现对待测物体相位信息的精确测量。

1 离轴数字全息的压缩感知重建原理

1.1 离轴数字全息

数字全息的记录过程是携带物体信息的光波O(x，y)与参考光R(x，y)在CCD光敏面发生干涉，所得到的干涉条纹图即为全息图［1］。其光强度表达式为

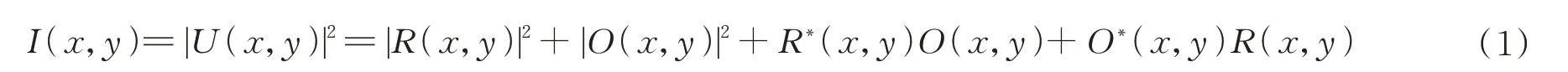
式中，第一、二项为零级衍射项，第三项为携带物体信息的干涉项，第四项为共轭像。通过频域滤波去除直流分量及共轭像，得到待测物光波的复振幅分布

角谱法是衍射光在频域内的一种传播形式，传播过程中无任何近似，可准确描述频域内的衍射再现过程［16］，其复振幅表达式为

式中，z为衍射距离，λ为波长，引入符号F，F-1分别表示傅里叶变换和傅里叶逆变换，F{U(x，y，0)}为物光波U(x，y)在像平面的频谱，H(u，v)为光传播的角谱函数。

1.2 压缩感知重建相位

压缩感知的信号采集过程是一个非自适应的线性采样过程，利用图像的稀疏性，通过非相关测量矩阵将高维信号投影到一个低维空间上进行观测感知。当选择合适的小波变换对物光波频谱信号进行稀疏表示时，可以利用压缩感知算法从少量频域数据中实现高精度重建。假设物光波的频谱信号x∈RN在稀疏基底Ψ=[ψ1，ψ2，ψ3…，ψN]下可表示为稀疏信号θ

用一个与稀疏变换矩阵不相关的高斯随机观测矩阵H∈RM×N(M≪N)对稀疏信号进行观测，得到高维信号投影在低维空间上长度为M的观测值I(M＜N)

式中，A=HΨ为M×N矩阵，称为感知矩阵，当感知矩阵满足稀疏信号的约束等距特性时，频谱信号的稀疏重构可以通过求解目标函数范数极值的方式，从少量压缩采样数据中准确重构出稀疏信号，再经过稀疏反变换获得原始高维图像信息。

压缩感知数字全息记录过程中的测量基相当于傅里叶测量矩阵，光学测量系统本质上探测到的是图像傅里叶变换后的频谱，根据衍射的角谱理论，衍射再现过程相当于不同纵向深度层面产生的离散物光点频谱与光在自由空间传播的传递函数的卷积。因此，全息记录可视为原物光场衍射强度的一个线性观测过程，对全息图频谱及物光场进行离散化处理，假设CCD的分辨率为Nx×Ny，像素尺寸为Δx×Δy，待测物体空间被划分为步长为Δx×Δy×Δz的Nx×Ny×Nz采样区间。对式（3）进行离散化可得

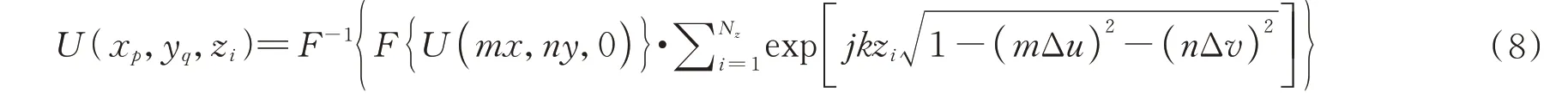
式中。

根据压缩感知理论数学模型，构建适用于描述频域中衍射再现的算法框架，首先要构建适应全息记录过程的传感矩阵，然后基于稀疏重构算法进行重构再现。为适应压缩感知理论中的线性观测过程，进一步需要将离散化后所表示的衍射光场与物光场的关系进行矩阵化处理。定义为全息图中第p行第q列的值为原三维物光场第i层第m行第n列的值。然后定义计算核Q=[q1q2…qNz]，并引入大小为(Nx×Ny)×(Nx×Ny)的分块对角矩阵B=bldiag(F2D，F2D，…，F2D)展开对原物光场的离散傅里叶变换计算，则

式中，F2D表示二维离散傅里叶变换为全息记录过程的感知矩阵。

通过对式（9）的线性观测模型进行优化求解，重构原物光波复振幅可得到相应的再现相位分布

式中，Im与Re分别表示复振幅的虚部和实部。

假设全息图的取样数为N×N，重建像平面的宽度为L=NT，即重建像平面每一个像素的间隔为T，物平面上的离焦点源在像平面上所占有的像素数即为

可以假定点源在重建平面的能量能够集中在1.5个像素作为焦深的限制条件［17］。定义数字全息重建图像的焦深为2|z-zi|，并令Nδ=1.5，根据式（11）得

式中，zi为理想像重建距离，z为实际像重建距离。一方面，重建图像的焦深随着理想像重建距离zi的增加而增加，当采样数N减小时，重建图像的焦深会增加；另一方面，由于全息图的采样是在物体的频域进行的，频谱经过FFT变换到空间域（重建平面），频率分辨率Δf与空间域的采样间隔T之间的关系为Δf=2π/(NT)，在采样间隔不变的情况下，通过减小采样数来获得较高的频率分辨率；由此可知，对于给定有限尺寸空间带宽的CCD，用基于压缩感知的压缩成像机制，通过频域稀疏采样，以远远小于传统方法所获得的数据量，得到重建平面较高分辨率的图像信息。

本文采用回溯思想的压缩采样匹配追踪（Compressive Sampling Matching Pursuit，CoSaMP）算法［18］对式（9）所表示的观测模型进行求解，从低维空间采样数据的非相关观测值中实现高维信号的感知。在傅里叶域内随机采样一半的频谱数据就能实现对全息图的稀疏重建，减小采样数来增加重建图像的焦深。在整个相位重建过程中，无需计算机模拟数字再现光照明全息图，消除了数字再现光对参考光的影响［19］。最后，利用（10）式计算得到包裹相位采用最小二乘相位解包裹算法［20］，得到待测物体真实的相位分布。

2 实验装置

采用Mach-Zehnder干涉光路，通过搭建数字全息显微测量装置，开展功能微结构光学元件的表面形貌和波前相位的高分辨测量实验。实验装置图如图1所示，系统中使用波长为638 nm的半导体激光器作为光源，激光器发出的点光源经过扩束准直（BE）后，经分光棱镜（BS1）1∶1分成两路，一路为物光，一路为参考光；物光波经过平面反射镜（M1）将光路转向，并透过待测物体，携带波前相位信息的物光波再经过显微物镜（MO₁）到达分光棱镜（BS2）；参考光经过平面反射镜（M2）转向经过显微物镜（MO₂）参考光通过设置一定量的离轴夹角，使得几种衍射像在成像平面上能够完全分离。参考光与物光在分光棱镜（BS2）处产生全息干涉，再经过Tube lens成像到CMOS相机的感光靶面上，实现数字全息图的采集。

图1 数字全息显微测量装置图Fig.1 Digital holographic micro measurement device diagram

CMOS相机（DMK 27AUC03）分辨率为1024 pixel×1024 pixel，像素尺寸为3.75 μm×3.75 μm；针对连续物体和不连续物体进行实验验证与分析，对不同深度的待测物体选用合适放大倍率的显微物镜进行预放大成像；微透镜阵列矢高为2.6 μm，选用10×显微物镜，相位分辨率板矢高为50 nm，选用20×显微物镜，实验中采用调焦位移平台进行精确聚焦，实验结果如图2所示，（a）为微透镜阵列全息图，（b）为相位分辨率板全息图。

图2 实验采集的数字全息图Fig.2 Digital hologram collected by experiment

3 实验结果及分析

3.1 微透镜阵列的测试与分析

为了验证压缩感知数字全息算法在提高相位重建质量方面的可行性，通过上述实验光路采集微透镜阵列全息图，如图3（a）所示；首先，对全息图进行傅里叶变换得到全息频谱图，如图3（b）所示，可以看出几种衍射像分离；然后，为消除零级衍射像和共轭像的干扰，使用合适大小的矩形滤波器提取正一级频谱并移中，再经逆傅里叶变换得到预处理后的全息图，如图3（c）所示；最后，对预处理的全息图，分别采用传统衍射再现的反向传播法（Back Propagation，BP）和基于压缩感知稀疏采样（Back Propagation-Compressed Sensing，BP-CS）的方法进行相位重建，获得其相位分布。黑色箭头为传统方法的重建步骤，蓝色箭头为本文所提方法的相位重建步骤，压缩感知稀疏采样算法框架，如虚线框图3（j）所示；采用传统衍射再现的方法得到的包裹相位分布，如图3（d）所示，基于压缩感知的方法重建得到的包裹相位分布，如图3（f）所示；传统的衍射再现过程是利用计算机模拟再现光照明全息图，经过衍射传输成像在像面上。而压缩感知稀疏采样的相位重建过程无需参考光波，其包裹相位不受数字再现光的影响；随后，采用基于离散余弦变换的最小二乘法对包裹相位进行解包裹处理，获得连续真实的相位分布。传统方法得到的解包相位，如图3（e）所示，压缩感知的方法重建得到的解包裹相位，如图3（g）所示；可以看出，基于压缩感知重建得到微透镜阵列的相位分布，相较于传统衍射重建方法，其相位图边缘轮廓清晰、背景平稳、相位对比度高，有更好的重建质量；本文采用相位畸变补偿算法来消除光学元件引起的相位畸变，得到微透镜阵列的二维相位图及三维相位图，如图3（h）、3（i）所示。

为验证本文方法三维重建的精确性，基于传统的数字全息再现得到的三维重建结果（BP）、基于压缩感知稀疏采样的三维重建结果（BP-CS）与白光干涉仪测量结果（ZYGO）三者进行比较，选取单个微透镜相同位置处的截面线（图3（h）中红线标出）进行对比，结果如图4（a）所示。将传统方法得到的重建结果、基于压缩感知稀疏采样的重建结果分别与白光干涉仪测得的结果进行残差分析，残差对比结果如图4（b）所示。对传统方法的相位重建结果与白光干涉仪之间的残差值R-BP，对基于压缩感知稀疏采样的相位重建结果与白光干涉仪之间的残差值R-BP-CS进行对比分析，采用峰谷差值（Peak-Valley，PV）和均方根值（Root-Mean-Square，RMS）作为评价指标，实验结果的评价参数见表1。

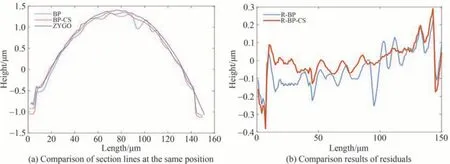
图4 微透镜阵列的三维重建实验结果Fig.4 Experimental results of 3D reconstruction of micro lens array

对基于压缩感知稀疏采样重建前后的相位结果分别进行计算，从表1中的残差对比可以看出，传统方法的三维重建结果与白光干涉仪测量结果在相同截面线处的残差估计：PV值为0.6975 μm，RMS值为0.127。压缩感知稀疏采样后的三维重建结果与白光干涉仪测量结果在相同截面线处的残差估计：PV值 为0.5094 μm，RMS值 为0.1079，后 者 残 差 的PV和RMS值 与 前 者 相 比，分 别 降 低 了26.97%和15.04%。结果表明，经过压缩感知算法处理后的波面较为平滑，恢复的相位精度更高，可有效提高相位重建质量。

表1 残差对比分析Table 1 Comparative analysis of residual

3.2 相位分辨率板的测试与分析

为了验证本文方法在不连续相位物体测量中的有效性，待测物体选用相位分辨率板，基于数字全息相位重建过程，本文在频谱滤波中用交互式掩模数字滤波实现正一级频谱的提取、移中。用压缩感知算法实现全息图频谱信息的稀疏恢复，再经过角谱法衍射再现其相位分布，得到相位分辨率板的三维重建实验结果，如图5所示。对比压缩感知重建前后的相位分布图，其中图5（a）为传统衍射再现的相位图，图5（b）为压缩感知稀疏采样重建得到的相位图，分别取第六组第2线、第8组第1线的局部截面线进行对比，如图5（c）、5（d）所示。分别计算相位分辨率板不同组线的峰谷差值（PV），传统方法（BP）的三维重建结果在6-2位置高度为47.6 nm、8-1位置高度为17.7 nm，压缩感知稀疏采样（BP-CS）的三维重建结果在6-2位置高度为49.6 nm、8-1位置高度为29.7 nm。相位分辨率板的纵向高度为50 nm的标准件，实际测量使用ZYGO白光干涉仪测得6-2位置处高度为53.0 nm，传统方法得到6-2位置处的高度与白光干涉仪所测结果进行误差计算，矢高的相对误差为10.2%；压缩感知重建后得到6-2位置处的高度与白光干涉仪所测结果进行误差计算，矢高的相对误差为6.4%，相对测量精度提高了3.8%。由此可知，压缩感知重建的方法计算所得到的相位测量精度更接近真实值。

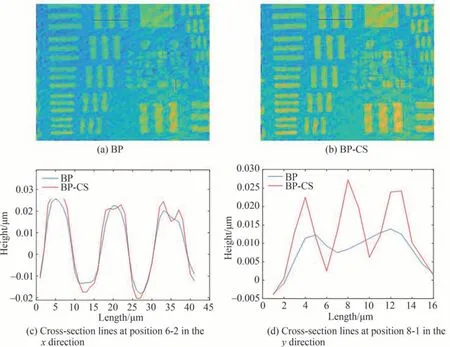
图5 相位分辨率板的三维重建实验结果Fig.5 Experimental results of 3D reconstruction of phase resolution plate.

通过图5（a）、（b）可以看出，传统数字全息再现算法的相位重建结果不能分辨第8组。由于CMOS相机离散采样的原因，对物体相位信息的离散化，更容易捕获随物光波连续变化的复振幅分布，使得部分角谱分量丢失。因此，在相位分辨率板的波前相位重建中，不能够分辨出局部不连续物体的相位特征。通过压缩感知稀疏采样恢复后的相位图，与传统衍射重建的相位图相比，其局部像质有所改善、相位对比度更高，对比相同位置处的截面线，能够分辨出第8组的第1线。这是由于压缩感知重建在频谱滤波后，频谱所占区域的宽度通常只是部分像素，通过变换域内的稀疏采样，对不连续区域出现的离散相位信息进一步压缩重建，使得重建图像更精细，说明不连续相位物体的局部频谱分量可以通过压缩感知的方式获得稀疏恢复。

4 结论

为了提高传统数字全息在三维重建中的相位测量精度，构建了离轴数字全息显微测量系统，提出了基于频域稀疏采样的压缩全息相位重建方法。该方法用基于压缩感知理论的压缩成像机制，通过低分辨的采样获得待测物波前相位的高分辨重建。通过对比压缩感知处理前后的三维重建精度，残差估计值的对比分析表明，该方法仅提取少量频谱数据依旧能够实现高精度相位重建，提高了微光学元件波前相位的重建质量以及三维测量精度。在不连续物体的波前相位测量中有着潜在优势，通过压缩成像来实现现有技术无法突破的超分辨检测成为了可能。