基于时间演化算符的高保真度量子操控的逆向工程
陈添凤,邱嘉旻,彭宏,陈曦,延英
(1 苏州大学光电科学与工程学院苏州纳米科技协同创新中心,江苏 苏州 215006)(2 苏州大学江苏省先进光学制造技术重点实验室教育部现代光学技术重点实验室省先进光学制造技术重点实验室,江苏 苏州 215006)(3 苏州大学数码激光成像与显示教育部工程研究中心,江苏 苏州 215006)
0 引言
近年来,在量子信息处理、量子计算、量子通信[1-4]等方面,对量子比特的相干操控引起广泛关注。在量子系统中,相干操控最重要的一个目标是对能量子态进行精确操控。但是,承载量子比特相干操控的物理系统通常都是不完美的,会受到退相干、频率失谐、非共振激发,以及拉比频率波动等因素的干扰和制约。因此,要实现精确的量子操控,需要尽可能地克服这些限制性因素的影响。目前,操控量子态常用的技术包括绝热通道技术[5-6]、共振脉冲技术[7],以及量子绝热捷径等。其中,绝热通道技术对实验中出现的参数波动具有较高的鲁棒性,但是因为受到绝热条件的限制,演化过程较慢,因此受退相干的影响较为严重;共振脉冲技术虽然有较快的演化速度,但是对参数波动的鲁棒性较差。为了兼得高鲁棒性和快速演化两个特征,上海大学的陈玺教授提出了量子绝热捷径(Shortcut to Adiabaticity,STA)技术[8-10]。该技术的核心是以非绝热方式(不需要满足绝热条件)来加速量子态的演化,同时保留了绝热过程的鲁棒性。
STA的实施方法主要有两种,一种是基于刘易斯-里森菲尔德不变量(Lewis-Riesenfeld Invariant,LRI)理论的逆向工程[11-14],另一种是无跃迁量子驱动(Transitionless Quantum Driving,TQD)[15-17]。前者的思路是首先求出哈密顿量的不变量,然后基于LRI的瞬时本征态来构建薛定谔方程的解,进而反解出系统的哈密顿量。后者的核心是在一个初始哈密顿量H0(t)上增加反绝热耦合项,使得量子态在系统总哈密顿量的驱使下能非绝热地沿着H0(t)的瞬时本征态进行演化。2010年,陈玺教授基于TQD提出仅在两个基态能级之间使用微波场就可以实现快速布局数转移[17],但是这个微波场在某些实验中较难实施。为此,研究者在三能级系统中,考虑到在大频率失谐情况下激发态没有布局数分布,因此可以将三能级系统简化为一个有效二能级系统,并确保在初始和终止时刻量子态的布局数与绝热状态时相同,基于TQD通过幺正变换,得到有效的哈密顿量,达到修改光脉冲的目的,实现了两个量子比特能级之间的布局数转移[18-19]。还有很多研究工作假设在三能级系统中不存在频率失谐问题(即共振模型),通过引入时间演化算符并结合逆向工程逆向求得哈密顿量,然后将此哈密顿量与初始哈密顿量进行对比获得修改后的光脉冲,进而实现高鲁棒性的量子态操控[18,20]。目前,这两种技术 已 被 应 用 于多种物理系统 中,如 囚 禁 离 子[21]、氮-空位(Nitrogen-Vacancy,NV)中心[22]、超导量子系统(Superconducting Quantum System)[5,23],以及稀土离子(Rare-Earth Ions,REI)量子比特系统[13]等,实现了对某些参数波动具有较高鲁棒性的量子操控。但是,这些工作大多仅关注量子操控的鲁棒性,而没有提及量子操控可能对系统带来的不必要干扰激发,即对目标量子比特进行操控的光脉冲可能会对邻近的非共振的量子跃迁进行激发,从而对目标量子比特造成干扰。例如在REI系统[24-27],对目标量子比特的操控会不可避免地对频域内临近的其它量子跃迁或背景离子进行非共振激发[13],进而对目标量子比特造成干扰。又例如,超导量子比特系统可以看作不等间距的量子谐振子,相邻三个能级之间的跃迁频率差值称为非谐量[28-29],对相邻两个能级的激发,会不可避免地激发其中一个到第三个能级的跃迁,为了减小这种干扰,一个方法是增大非谐量,但是付出的代价却是降低量子比特的相干时间。因此,在类似这样频率紧密分布的系统中,要想取得高保真度的量子操控,不仅需要快速和高鲁棒性的特征,还需要极低的非共振激发。
为了使量子操控具备上述三个特征,快速高效地制备量子比特的任意叠加态,课题组已基于LRI逆向工程理论[13,30],结合光脉冲优化方法,在三能级系统中创建了快速、具有高鲁棒性和低非共振激发的量子操控,并将之应用于REI系统中,得到了较好的结果。然而,在LRI理论中,首先需要构造出哈密顿量的不变量,而在大多数系统中,不变量是未知的,构造不变量的过程较复杂,会受到某些实验系统的限制[9]。TQD与LRI在一定程度上是等效的,二者之间可以互相转换[16]。因此,原则上基于TQD也可以创建满足需求的量子操控。但是,在TQD方案中引入的反绝热耦合项[17],在很多情况下是直接耦合两个量子比特能级(0和的微波脉冲,而在一些实验系统中,这种微波场不容易实施或不适合使用[31]。比如,在稀土离子量子比特系统中,为了对量子比特进行有效的操控,首先需要通过光谱烧孔效应创建一个零吸收窗口,然后再将一小部分(频率分布宽度约170 kHz)稀土离子泵浦回透明窗口中作为量子比特[24]。在创建零吸收窗口时,必须使位于吸收窗口左侧的稀土离子都处于态。若在量子操控中使用微波场,它会对这些离子在两个量子比特能级和之间进行激发(这个跃迁的非均匀展宽非常非常小,可以忽略不计),导致部分离子会被泵浦到零吸收窗口中,对目标量子比特造成干扰。因此,在稀土离子量子比特系统中不适合使用微波场。为此,福州大学夏岩教授课题组提出,基于一组含时辅助基矢来构建时间演化算符,并结合逆向工程得到哈密顿量,进而通过约束基矢中的两个含时参量之间的关系来消除哈密顿量中的反绝热耦合项,在非绝热状态下实现了布局数转移[32]。
本文同样基于TQD的逆向工程技术,通过合理设计时间演化算符,消除哈密顿量的反绝热耦合项,同时去除额外的微波场;并将此理论方案应用于频域紧密分布的稀土离子量子比特系统中,在非绝热光脉冲中引入多个新自由度参数,在不改变初始态和终止态的情况下,通过优化这些自由度参数的取值来改善光脉冲的工作性能。一方面增加量子操控对频率失谐量的鲁棒性;另一方面,使量子操控在对目标量子比特作用时,对临近量子比特造成极低的干扰激发。同时,本方案是一个非绝热过程,可大大缩短脉冲作用时间,降低退相干的可能性。
1 光脉冲的设计理论
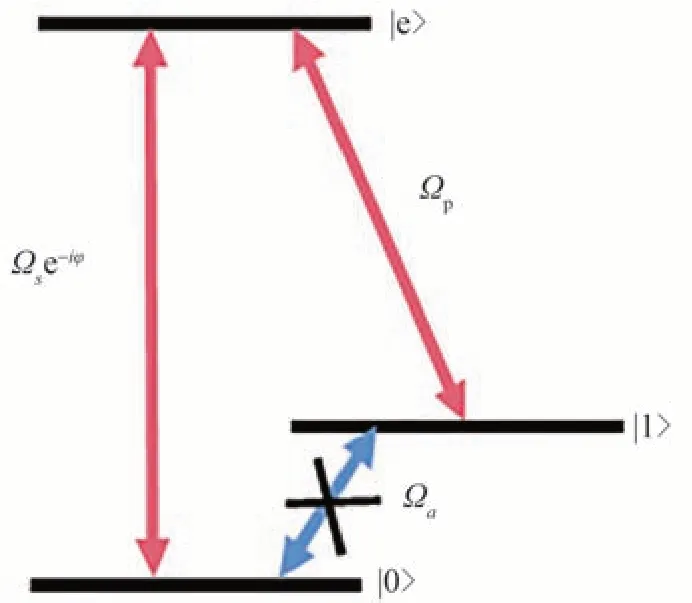
图1 一个Λ型三能级系统的能级结构示意图Fig.1 The schematic energy level diagram of a three-level system with Λ configuration

首先,基于两个含时变量α(t)和β(t),在基矢下假设一组正交归一且完备的辅助态基矢,即

基于这组基矢,系统的时间演化算符可以构建为[32]
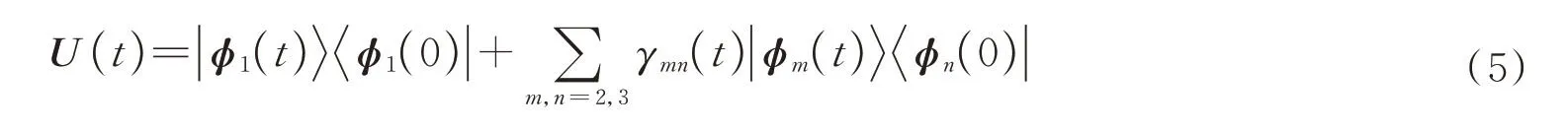
由于U(t)U†(t)=I,参数γmn(t)需要满足

式中,δmn是Kronecker Delta函数。在式(6)的约束下,可以借助另一个含时参量l(t)将γmn(t)表达出来,于是式(5)变为

由此得到系统的哈密顿量在辅助态基矢下的形式,即


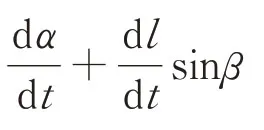
至此,借助三个含时参量构造出了时间演化算符,并逆向求解出系统的哈密顿量,通过约束三个含时参量之间的关系,在三能级系统中将两个量子比特能级之间的直接耦合项去除掉。
结合式(1)、(10),可得到光脉冲Ωp,s(t)的表达形式为

这样,基于两个含时变量α(t)和β(t)得到了光脉冲的拉比频率;对光脉冲的设计问题转换为构建α(t)和β(t)的问题。另外,考虑到在实验中,如果光脉冲振幅在时域中有急速变化,那么它必然会在频域内带来多个冗余分量,可能对目标量子态造成干扰。因此,光脉冲的振幅最好在起始和终止时刻都为零,即

这要求α(t)和β(t)满足如下边界条件

本文目标是使哈密顿量H(t)驱动三能级系统在两个量子比特态能级之间进行精确演化,将量子比特初始化到一个任意叠加态上。量子操控的精确度用保真度F来衡量,即

基于以上理论考虑一个最简单的情况,即哈密顿量驱动系统沿着从初始态演化到目标叠加态。即α(t)和β(t)必须在初始和终止时刻满足如下边界条件

考虑到式(13)以及高鲁棒性和低非共振激发的要求,提出α(t)和β(t)为

式中,ak(k=1,2,3,4…)是不含时的常数,表征每个正弦函数的权重;C为一常数,其取值可以在满足α(t)的边界条件下进行选取,这里令C=0。式(17)和(18)所示α(t)和β(t)显然满足式(15)和(16)要求的边界条件。为满足边界条件式(13),ak(k=1,2,3,4…)需要满足

由式(19)、(20)可知,n个参数中(a1,a2,a3,a4,…an)仍然有n-2个自由度,这些自由度可以用来对光脉冲进行优化。因为在不考虑频率失谐和非共振激发的前提下,无论ak取何值,量子态都可以完美地沿着进行演化,达到目标态。但是,在REI系综量子比特系统中,系综量子比特中的频率失谐和光脉冲对附近量子比特的非共振激发都会降低量子操控的保真度,借助这些自由度可以优化光脉冲的工作性能,实现高保真度的量子操控。

在式(19)和(20)中,n的取值原则上可以无限大,这样提供更多的空间去调节光脉冲的工作性能,但是n越大,相应正弦波的频率就越高,而在实际应用中,正弦波的频率可能会受到所使用仪器设备的时间精度的限制。因此考虑n=4的情况,即值得指出的是,前文所述理论方案考虑的是哈密顿量驱动系统沿着演化的情况,但事实上,对于所述初始态和目标态,哈密顿量也可驱动系统沿着另外一个路径演化,即沿,实现既定的量子操控。此时,式(5)所示的时间演化算符应该调整为相应地,式(15)和(16)也要发生改变,但是,逆向设计的基本原理保持不变。但是,系统不可能沿进行演化,因为要求态上的布局数时时刻刻为零,这点在使用两个光场间接地对两个量子比特能级进行耦合时是不可能实现的。
2 数值模拟
将理论方案应用于REI系统中(Pr3+:Y2SiO5),考察是否可以创建快速、高鲁棒性和低非共振激发的量子操控。REI系统具有长达6 h的量子比特相干时间[24-27],是一个有竞争力的量子计算硬件的测试体,而且晶体材料的制作工艺成熟,可以直接采购。在REI系统中,极少量的Pr3+以随机掺杂的方式取代硅酸钇晶体中的钇离子。研究者通常选取Pr3+基态中两个超精细能级作为量子比特,这两个能级之间的耦合通过各自与激发态之间的光学跃迁来实现,相关的能级系统都可以看做一个三能级型系统。在这样的系统中实现精确的量子操控,除了快速以外,还需要满足两个条件:1)量子操控对表征量子比特的数十亿个镨离子(称为系综量子比特)具有同等效果的激发,即对约170 kHz(半高全宽)的频率失谐量具有高鲁棒性[24];2)由于晶体中原子密度极高,所以在目标量子比特跃迁频率附近(≥3.5 MHz)存在着大量的非共振Pr3+离子,称为背景离子。这就要求量子操控对这些背景离子尽可能地不要有任何激发,即量子操控必须具有足够低的非共振激发[25]。

图2 光脉冲拉比频率和量子态布局数随时间的演化情况Fig.2 Time evolution of the Rabi frequencies of the pulses and the population of the quantum state
2.1 高鲁棒性
为了考察上述光脉冲对于REI系综量子比特中频率失谐量Δ的鲁棒性,在三能级耦合微分方程中引入了频率失谐量,并考察了在脉冲终止时刻,量子比特达到目标量子态的保真度对频率失谐量Δ之间的依赖关系,结果如图3所示。在±170 kHz频率失谐范围内,设计的光脉冲对系综量子比特的平均操控保真度为99.86%,比文献[13]中的结果(99.79%)略高,说明量子操控具有较好的鲁棒性。作为对比,在ak的有效取值范围内随机取了一组值:a1=-,a2=0,a3=0,a4=,此时光脉冲对系综量子比特的平均操控保真度为98.23%。

图3 获得目标态的保真度对频率失谐的依赖关系Fig.3 Dependence of the fidelity of achieving the target stateon the frequency detuning
2.2 低非共振激发
除了对频率失谐量的鲁棒性以外,还关心光脉冲在对感兴趣的量子比特进行操控时,是否会对其邻近频域的背景离子或其它量子比特造成非共振激发。即在理想情况下,如果不存在非共振激发,那么背景离子应该保持在其初始状态上的布局数与频率失谐量之间的依赖关系,结果如图4所示。对于|Δ|=3.5 MHz处的量子比特离子,在态上上。为此,考察了在光脉冲结束时刻,量子态在能级的布局数(蓝色曲线)低于3%;随着频率失谐量的增加,在1态上的布局数逐渐降低;在|Δ|≥5 MHz时,背景离子被非共振地激发到态上的概率低于1.45%。在3.5 MHz时的非共振激发概率比文献[13]中结果(2.7%)略高,但是仍然在可接受的范围内,尤其是选择能级间距更大的稀土离子作为工作物质时,如Eu3+。
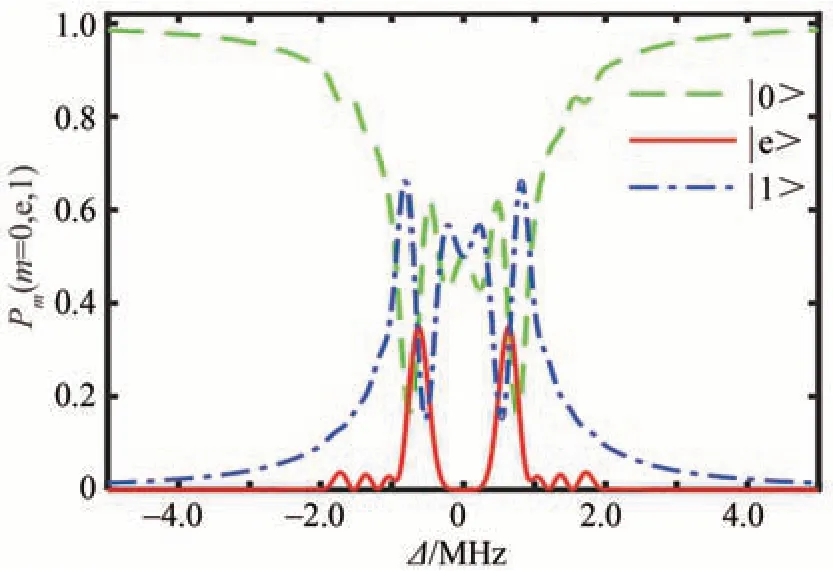
图4 量子态在能级和上的布局数对频率失谐的依赖情况Fig.4 Dependence of population in levelandof the final stateon the frequency detuning
数值模拟结果表明,设计的光脉冲既对于系综量子比特中存在的频率失谐(≤170 kHz)具有高鲁棒性,也对于位于目标量子比特寻址频率附近的(≥3.5 MHz)背景离子具有极低的非共振激发,符合REI系统对量子比特进行高保真度操控的需求。
3 实验方案
图2(a)所示的光脉冲在实验中是切实可行的,可以通过连续激光和声光调制器等设备来产生,实验装置示意图如图5所示。首先,使用任意波形发生器(AWG)生成两个无线电脉冲(RF)信号,它们的振幅与式(11)所示拉比频率成正比,位相与光脉冲的位相相同,即

图5 实验装置图Fig.5 The schematic experimental setup

式中,A为从光脉冲的拉比频率Ωp,s到无线电信号振幅Ep,s的转换系数,由实验系统决定;E01是两个量子比特能级和之间的能级差;h是普朗克常数。RF脉冲驱动声光调制器(AOM),使之对入射的连续激光调制,这样AOM输出的一阶偏折光束便是所需的光脉冲,其时长、振幅、位相等参数全部由AWG生成的RF信号决定。当光束聚焦直径为100 μm时,一阶偏折光束的典型上升时间为数十纳秒。因此,基于此系统可以生成如图2(a)所示的光脉冲。
由式(23)、(11)、(17)和(18)可见,ak的取值决定了RF信号的波形。而在实验中,每个AWG都有特定的时间分辨率和振幅分辨率,通过数值计算得到的最优ak值,如果使RF信号的振幅变化太快,超过了AWG的时间分辨能力,或者ak中小数点后最后一个数位上的数值对应的RF信号的振幅变化低于AWG的振幅分辨率,那么所生成的RF信号就会偏离理想波形,这种偏离会影响AOM的声光调制作用强度,使得生成的光脉冲也偏离理想波形。因此,有必要考察操控保真度对ak在其最优值附近的波动的依赖程度,这可以为实验研究提供一些参考。鉴于本文给出的最优值中,a1和a2远大于a3和a4,因此,有理由相信a1和a2对保真度的影响会更大,为此,考察了保真度对a1和a2波动的依赖关系(Δ=0),结果如图6所示,图中代表着a1和a2在最优值附近的相对波动。在η1=±10%,η2=±10%区间内,即图中红色点线方框内,绝大部分情况下保真度仍大于99%。

图6 在Δ=0下,保真度对a1和a2值波动的依赖关系Fig.6 Dependence of fidelity on the fractional fluctuation of a1 and a2 withΔ=0
4 与无跃迁量子驱动技术的对比
本文提出的理论方案,与传统的无跃迁量子驱动方案相比,相似之处是二者都通过构建时间演化算符逆向求解出系统的哈密顿量,且都涉及到两个量子比特能级之间的直接耦合项,但存在着显著差异。本文理论方案具有如下特征:1)量子态沿着辅助态进行演化,而不是初始哈密顿量的瞬时本征态。辅助态由两个含时参量α(t)和β(t)来决定,在满足边界条件的情况下,α(t)和β(t)可以有多种选择,使得辅助态具有更大的调节空间。2)通过逆向设计哈密顿量消除了微波场,不但可以简化实验装置,而且可以为某些无条件或不适合使用微波场的实验系统,如REI系统,带来极大便利。更重要的是,采用本文方案消除掉0和1之间的直接耦合微波场,只需要使三个含时变量α(t)、β(t)和l(t)满足关系式=0即可,不需要在其他任何方面付出代价。即式(5)所述时间演化算符提供了自由度,对于任意形式的α(t)和β(t),总可以根据=0找到一个l(t)。但是,光脉冲的数目和具体形式如式(11)所示,却不依赖于l(t),所以不会受到任何影响。3)在含时参量中引入多个自由度,使哈密顿量的构造具有更高的灵活性,可用来调节光与物质相互作用的动力学行为。
5 结论
本文借助一组正交归一的辅助态,构建出时间演化算符,并由此逆向推出系统的哈密顿量;通过约束辅助态中的含时参量之间的关系,消除了哈密顿量中的微波场,简化实验操作步骤。同时通过在含时参量中引入多个自由度参数并对其值进行优化,设计出了非绝热的、对较小范围(|Δ|≤170 kHz)的频率失谐量具有高保真度,且对临近量子比特(|Δ|≥3.5 MHz)具有较低非共振激发的量子操控光脉冲。将此理论方案应用于REI量子系统中,数值模拟表明,该光脉冲可以操控系综量子比特创建一个任意叠加态,平均操控保真度高于99.86%。
本文提出的理论方案不仅适用于稀土离子量子比特系统,也适用于其它任何依靠频率寻址的量子系统,如氮-空位中心系统,超导量子比特系统等。另外,还可以结合微扰理论,将此理论方案进行拓展,使量子操控在对频率失谐量具有高鲁棒性,对邻近量子比特具有低非共振激发的前提下,进一步对拉比频率波动也具有较高的鲁棒性。克服这些物理限制性因素对量子操控的影响,对量子计算、量子纠错以及量子通信等量子科技都具有积极的意义。
附录
如引言中所述,期望量子操控能对REI系综量子比特中存在的频率失谐量具有高鲁棒性,即在||Δ≤170 kHz时,保真度要尽可能地趋近于1;而对距离目标量子比特约3.5 MHz以外的背景离子不产生干扰,即在||Δ≥3.5 MHz时,非共振激发要尽可能地低。为此,对式(17)中的参数ak进行优化。采用的方法是对ak在其有效取值范围内进行扫描,考察量子操控在||Δ≤170 kHz范围内的保真度,以及在±3.5 MHz处的非共振激发。保真度越高,非共振激发越低,参数的取值就越优越。
具体步骤为:
首先,式(21)和(22)限定了a3和a4必须在[-1,1]范围内,对于在此范围内的任意值,a1和a2都可以由此二元二次方程组求出。为了清晰地看到这两个参数对量子操控保真度和非共振激发的影响。令Δ=170 MHz,对它们进行了扫描,保真度对a3和a4的依赖关系如图7(a)所示;同时,在Δ=3.5 MHz处态上的布局数P1对a3和a4的依赖关系如图7(b)所示,P1越低,说明非共振激发越低。图7(a)和7(b)的交叠区域是感兴趣的参数空间,在此交叠区域中a3的取值范围是[-0.07,0.14]。

图7 光脉冲对系综量子比特的操控保真度F以及对背景离子的非共振激发P1对a3和a4的依赖关系Fig.7 Dependence of the operational fidelity F over the ensemble qubit and the off-resonant excitation P1 of the background ions on a3 and a4
其次,为了在前一步得到的范围内对a3和a4的取值进行更精细的优化,令a3=0.05,对a4在其有效取值范围内(a3ϵ[-0.5,0.45])进行扫描,寻找出保真度F=0.99时对应的频率失谐量值Δ1和Δ2。由此可得出,保真度大于等于0.99的频率失谐量范围为。同时,考察频率失谐量Δ=3.5 MHz时所对应的非共振激发P1的值(从图4可以看出,P1对于频率失谐量呈对称分布,因此这里只考虑了3.5 MHz时的情况),结果如图8所示。理想的结果是在确保P1足够小(例如<3%)的前提下,Γ的值越大越好。从图中看出,当a4=-0.17时,Γ=0.38 MHz,P1=3.0%,量子操控兼具高鲁棒性和低非共振激发的特性。此时,根据式(20)和(21)可以求出a1=-0.74836,a2=0.63918,即文中采用的最优值。需要指出的是,最优值有多种选择,文中给出的只是一组。

图8 保真度F≥0.9对应的频率失谐量区间Γ以及在Δ=3.5时态上的布局数P1对a4的依赖关系Fig.8 Dependence of the range of the frequency detuningΓwith F≥0.99 and the population instate P1 withΔ=3.5 MHz on a4

