高精度背景纹影流场探测系统研究

刘世韦，梅海平，任益充，陶志炜，艾则孜姑丽·阿不都克热木，张骏昕，李艳玲，饶瑞中

（1 中国科学技术大学 环境科学与光电技术学院，合肥 230026）（2 中国科学院合肥物质科学研究院 安徽光学精密机械研究所 大气光学重点实验室，合肥 230031）

0 引言

流场显示与测量技术广泛应用于航空航天、大气海洋、医学生物等领域，对了解流动现象、研究流场特性、探索物理机制等具有重要意义［1］。粒子示踪和表面流动技术适用范围有限且会干扰待测流场，光学测量方法具有非接触、无干扰的显著优势，但干涉法费用昂贵且易受到环境干扰，传统的阴影和纹影技术定量化程度不高。随着计算机软硬件的成熟，20世纪末，MEIER G E A等［2］在传统纹影技术的基础上，结合粒子图像测速（Particle Image Velocimetry，PIV）技术创造性的发展出了一种非接触式新型流场探测手段，即背景纹影（Background Oriented Schlieren，BOS）技术，BOS技术以其不干扰待测流场、时空分辨率高、视场大、成本低等优势迅速发展并广泛应用于多种流场测量显示，如直升机桨叶旋涡、风洞、超声速流场等［3-5］。BOS技术不仅在应用上表现出巨大的潜力，在理论上的发展也逐步推进，文献［3，6-9］分别讨论了背景纹影技术的原理、背景设置、以及在流场测量中的精度、灵敏度、分辨率等问题，使得BOS技术的原理和计算方法日趋成熟，应用更为科学和精密。国内关于BOS技术的研究起步较晚，2010年起，国防科大率先开展BOS技术在气动光学领域的实验研究［10］，其后被用于燃烧场诊断、温度场可视化、密度场重构等，为实现大视场流场研究提供了经验。

背景纹影技术的核心在于使用图像处理算法对未经过流场的原始背景和经过流场后的扰动背景进行比对，进而计算各像素点的位移，因此背景和图像处理算法的选择在BOS技术中占有很重要的地位。背景图案通常分为随机点图、规则点图等，图像处理算法包括互相关算法、光流算法、整像素搜索+亚像素定位［11］等。经过多次定性的实验验证，可知随机的背景图案效果优于规则背景，光流算法在速度、精度和鲁棒性优势明显［12］，但是光流算法类型和具体的背景参数对流场定量测量的影响以及系统可实现的检出精度，目前仍缺少系统性的研究和论述。此外，背景纹影技术得到的是背景像素点的偏移量，此偏移量代表着流场的折射率梯度，理论上由梯度场可以重构折射率场，在研究流场结构、流体特性等方面都有重要意义，因此我们将波前重构与背景纹影技术结合起来实现流场中的波前探测。

本文首先分析不同类型的光流算法以及不同参数的背景对图像位移检测精度的影响，并探究在最优背景和最佳算法下BOS系统可检测到的最小位移量，即系统的位移检测精度；在此基础上根据背景图像位移场与流场波前梯度场的定量关系，分别采用傅里叶变换法和迭代法重构流场波前，并进一步分析其波前重构精度；最后分别开展以散斑图像为背景的室内酒精温压场实验和以自然图像为背景的室外炮筒声压场实验，通过实验论证实验室和外场环境下不同流场测量的可行性。

1 背景纹影技术原理

如图1所示是背景纹影成像系统，其主要由背景图案、扰动流场和成像系统三部分构成。扰动流场使得大气的折射率出现随机起伏，产生的折射率梯度使得来自背景图案的光线以一定的偏转角发生偏折，从而使光线透过镜头入射至CCD上的位置产生偏移。光线从背景图案到达CCD具体过程为

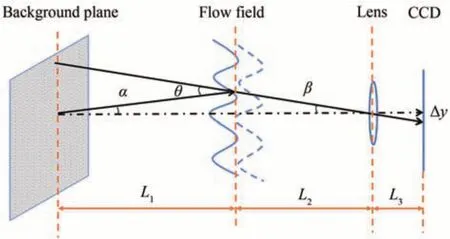
图1 背景纹影系统成像装置Fig.1 BOS imaging configuration

1.1 光线偏折

由经典光学可知，偏折角是折射率梯度沿光传播路径的积分，而光程（Optical Path Length，OPL）是折射率沿光传播路径的积分

式中，θ是偏折角，n是折射率，∇表示梯度，dL是光传播路径的积分变量。

在实际中，我们通常测量光程差（Optical Path Difference，OPD），OPD是各点OPL与OPL在光瞳处的平均值之差，当流场以及流场条件一定时，平均OPL为定值，所以有

联立两式可知

1.2 像点偏移

当折射角满足小角度时有

由几何关系可知

所以，偏折角满足

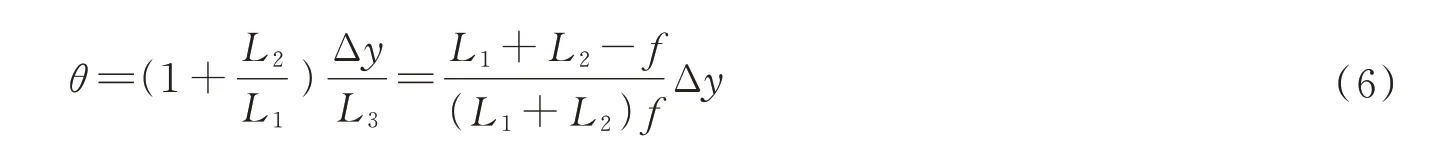
式中，L1是背景板到流场中心的距离，L2是流场中心到镜头的距离，L3是CCD到镜头的距离，Δy是背景斑点偏移量，f是镜头焦距。

理论上由位移场可以得到折射率梯度场，进而重构出折射率场，得到波前信息。

2 位移提取算法及其精度

由上述原理可知，BOS技术首先计算出CCD接收平面上每个像元的偏移量，再根据偏移量求解流场的波前分布情况，其中偏移量求取的算法精度直接影响最终精度，因此开展位移提取算法精度测试并确定其位移检测精度。

2.1 光流算法

背景纹影技术是通过比较光线经过流场前后的两幅图像像素点的偏移来进行光线偏折角的量化，而在位移提取的算法中，光流算法是通过时变图像序列中像素点的亮度变化来估计实际运动［13］，二者都是要解决图像像素对应问题，因此我们在BOS技术中使用光流算法。

光流算法首先假设相邻帧像素点“亮度一致”，即

I(x，y，t)和I(x+dx，y+dy，t+dt)分别是图像序列中时刻t和t+dt时的图像亮度。将右式进行泰勒展开并舍去高阶项后得到光流场的基本约束方程［17］

Ix，Iy，It分别表示像素点灰度沿x，y，t方向的偏导数，可由图像数据得到，u，v是像素点沿x，y方向的光流矢量，是未知量。

该方程属于超定方程，需要引入额外的约束条件进行求解，根据所得光流矢量疏密程度可分为稀疏光流和稠密光流。稀疏光流以L-K光流算法［14］为代表，在光流基本方程的基础上附加一个局部平滑假设，通过选取特征点进行图像的局部匹配；稠密光流以H-S光流算法［13］为代表，在光流基本方程基础上附加一个整体平滑假设，通过计算图像上所有的点的偏移量得到光流场。稀疏光流计算速度快，多用于追踪运动物体，而在流场研究中更多需要还原其运动细节，稠密光流适用性更强。

2.2 光流算法精度测试

为了可精确控制背景参数及其位移量，采用亚像素平移方法，通过比较数字图像算法计算结果和实际加载量的偏差来估计算法精度。具体方法为：

1）用激光衍射的快速傅里叶变换方法数值模拟高斯激光束散斑背景图［15］；

2）采用双线性插值方法将背景图进行亚像素平移；

3）将原图和平移后的图像用数字图像算法进行处理，对比处理结果与实际位移量。

由2.1可知，光流算法是通过比较背景图像中像素点的亮度变化来估计实际运动，而且光流算法根据约束条件的不同又可分为多种类型，因此背景图案、算法类型都可能对精度产生影响，本文分析了五种不同的光流算法以及不同亮度、对比度和相关度的背景对位移检测精度的影响。

2.2.1 算法类型及参数对光流算法检测精度的影响

如2.1所述，稠密光流求解的超定方程需引入额外的约束条件，根据约束条件的不同，光流算法可分为很多种。Farneback将图像视为二维信号并展开为多项式，用加权最小二乘法进行位移估计得到稳健的稠密位移场；Wulff基于金字塔LK稀疏光流，通过匹配插值得到快速的稠密光流；Weinzaepfel在变分光流法中引入描述子匹配，用于计算大位移光流；Black假设任意光流场可以近似为少量基本流场的加权和，建立分层模型，通过主成分分析从稀疏得到稠密光流；Zach基于全变差正则化和数据保真度项中L1范数的双重公式，采用逐点阈值化有效计算光流［16-19］。根据上述光流原理分别实现了Farneback、SparseToDense、DeepFlow、PCAflow和DualTVL15种稠密光流算法。

基于这5种稠密光流算法对相同参数的散斑背景进行亚像素位移检测，在python3.8下处理，所用计算机配置为：8 GB内存，Intel（R）Core（TM）i5-8265U CPU处理器，1.80 GHz主频，检测结果如图2（a）所示。Deepflow和Dual TVL1速度偏慢且误差较大，PCAflow和Sprasetodense速度较快但在不同位移量下稳定性较差；综合比较，采用Farneback算法用时最少、误差最小且稳定性最高，在稠密光流算法中精度最高。

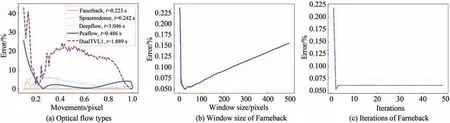
图2 不同光流算法类型及参数下检测量与实际位移量的相对误差Fig.2 The relative error between the measured displacement and the actual displacement under the different optical flow

Farneback算法中的参数对位移检测精度的影响如图2（b）和图2（c）所示，可以看到，当散斑图移动0.2个像素、迭代次数不变，均值窗口大小在2～500个像素之间变化时，尺寸在10个像素左右时，误差最小，当小于或大于10时，误差都会增大，这是因为平均窗口与算法鲁棒性有关，窗口过小可能使位移量溢出，过大又会增大平均效应使运动场模糊；当散斑图移动0.2个像素、均值窗口大小不变，迭代次数在1～50之间变化时，图中所有迭代次数下误差均在可信范围内，其中迭代不小于2次时误差较稳定，这是因为迭代次数与检测速度有关，迭代次数多与理论值越接近但是速度会减慢，当移动亚像素时，较少的迭代次数就可以达到很高的精度。因此，均值窗口尺寸会影响检测精度，其大小应当根据像元的位移来确定，迭代次数影响较小但不应过多否则耗时较长，通常可设为3。

2.2.2 背景图像参数对光流算法检测精度的影响

背景亮度B反映了图像的明暗程度，用平均灰度来衡量；对比度C反映了图案的清晰程度，用局部像素的灰度差来衡量；图像的相关度F反映了图案的相似程度，用局部像素的灰度相关性来衡量。

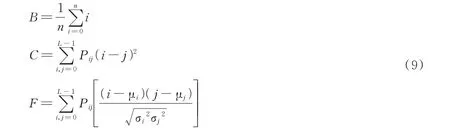
式中，n是像素点的个数，L是灰度值的级数，i，j分别是图像上任意两点的亮度值，Pij是整幅图像中(i，j)的概率组合，μx，μy，σx，σy分别为和的均值和标准差。

图3（a）是相关度、对比度相同而亮度依次增加的背景图分别移动不同亚像素位移量时的检测结果，随着亮度的改变，相对误差不变，可以认为在一定范围内图像亮度对精度几乎不产生影响；图3（b）是相关度、亮度相同而对比度依次增加时的检测结果，对比度较低时，测量的相对误差较大，随着对比度的增加，相对误差逐渐减小，当对比度大于一定范围时，相对误差几乎不变，可推知对比度在一定范围内对精度会产生较大影响；图3（c）是平均亮度、对比度相同而相关度逐渐增加的检测结果，当相关度非常小时，相对误差也非常小且变化不大，而当相关度逐渐增大时，相对误差也增大，可知图像相关度会影响光流算法的检测精度。

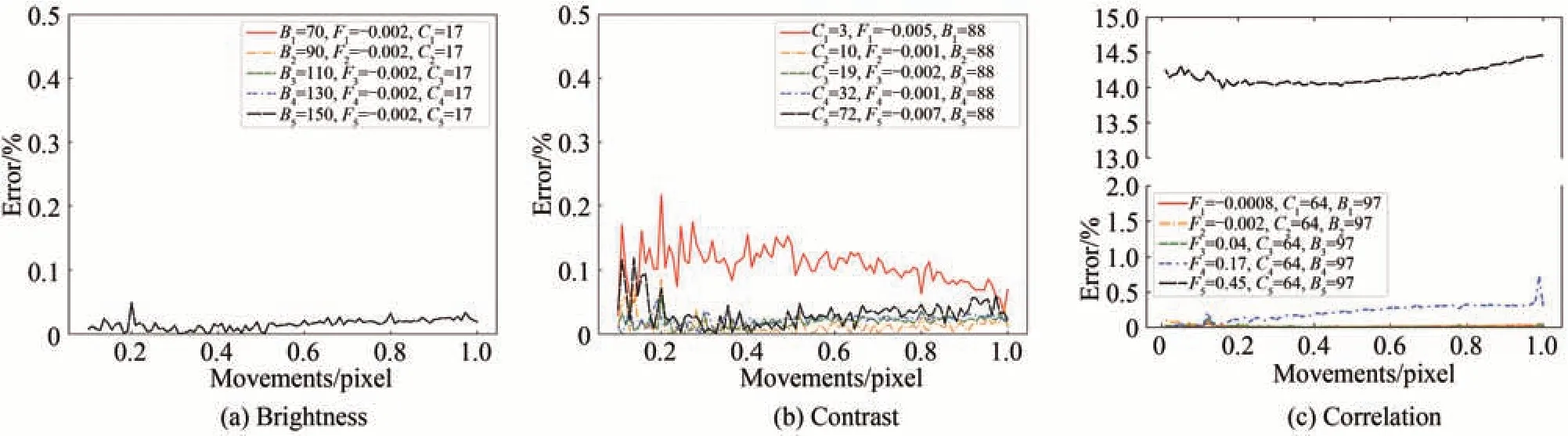
图3 不同背景参数下检测量与实际位移量的相对误差Fig.3 The relative error between the measured displacement and the actual displacement under the different background parameters

综上所述，光流算法检测精度与背景图像相关度呈反相关，相关度较小意味着图像纹理密集，此时细微的位移对子窗口内的图像造成较大影响，故检测算法能够实现较高精度；光流算法检测精度与图像对比度则呈现正相关，对比度较高时意味着图像明暗差别较大、纹理边缘更为清晰，从而更易于检测微小位移；正常曝光情况下，图像亮度对光流算法检测精度几乎无影响，这是因为图像亮度意味着整体明暗程度，在一定范围内调节亮度不会改变图像纹理，检测精度不会变化，但是亮度过大或过小时图像会出现过曝和欠曝现象，此时图像纹理趋于平滑，位移不明显，相对误差也会增大。

2.3 光流算法位移检测精度

为验证光流算法的位移检测精度，用如图4（a）的散斑图案作为背景，背景参数为：亮度97，对比度64，相关度-0.008；通过双线性插值将其依次移动1/10，…，1/500个亚像素；并用Farneback稠密光流算法处理背景图像和位移后图像，算法参数为：均值窗口10，迭代次数3；比较实际位移值和测量值，结果如图4（b）所示。虚线是实际位移值，实线是测量值，当位移量大于0.0050个像素时，虚线与实线基本重合，而当位移量小于0.0050个像素时，实线逐渐偏离虚线，说明随着位移量的减小，测量值逐渐偏离实际位移值，检测误差逐渐增大。

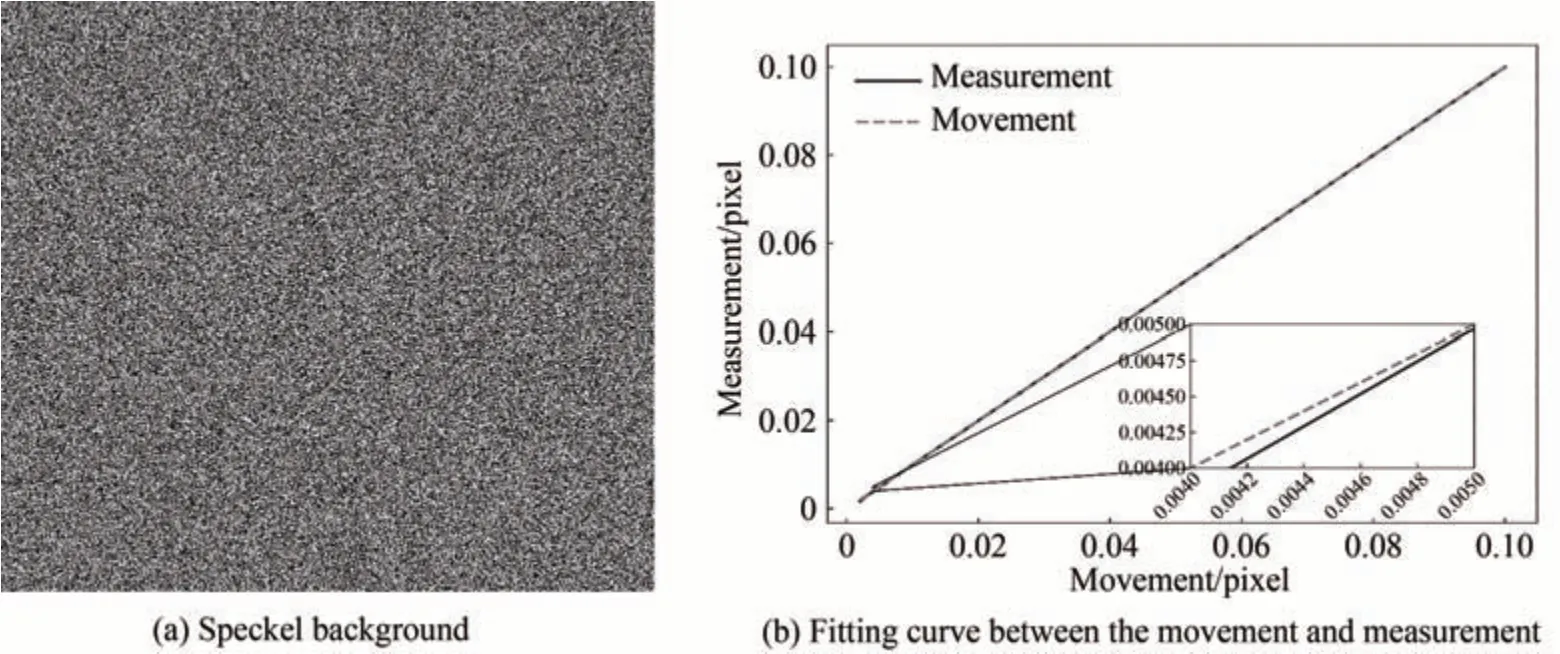
图4 背景在不同位移量下真实值与测量值的拟合Fig.4 Fitting curve between the movement and measurement of background under different displacement

对图4（b）中的测量结果进行高斯统计和误差分析，结果如表1所示，表1是背景沿水平方向和竖直方向分别移动1/10、1/50、1/100、1/200、1/300、1/400个亚像素时的测量值、99%的置信区间和相对误差、不确定度。相对误差S是测量值绝对误差与实际位移值之比，它反映了测量值的可信程度，一般认为相对误差在5%以内都是可信的，不确定度U是测量值的标准偏差，它反映了测量值的分散性程度，可用于评价测量值的质量优劣，不确定度越小，质量越高。当位移量达到0.0025个亚像素时，竖直方向检测误差为5.27%，超过可信范围，因此光流算法检测精度可以达到1/400个亚像素。

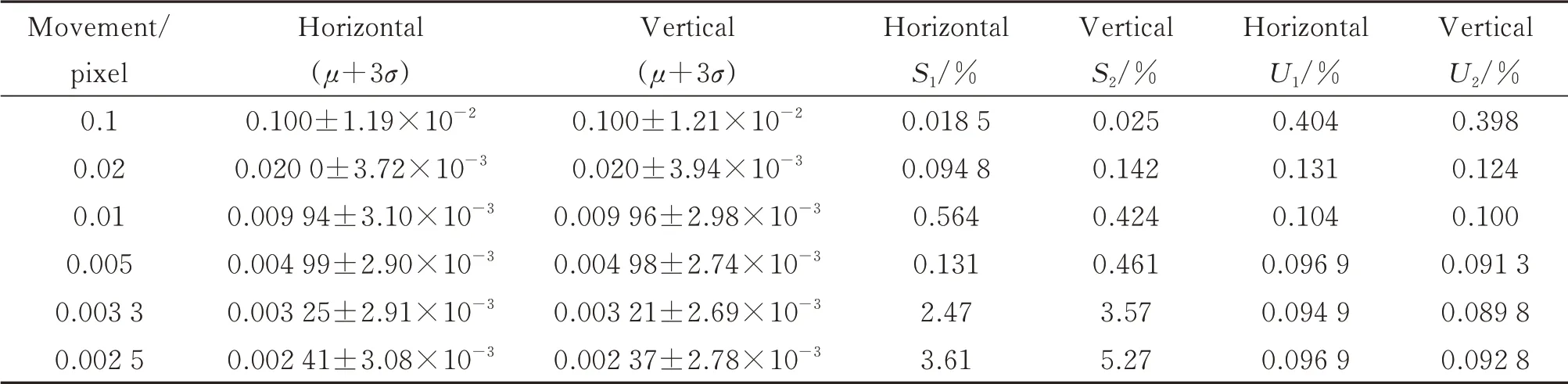
表1 不同位移量下，水平和竖直方向的测量值、相对误差和不确定度Table 1 The values，the relative error，the uncertainty in horizontal and vertical directions between the measured displacement and the actual displacement under different displacements

3 波前重构算法及其精度

通过光流法获得图像中偏移量即各像素的折射率梯度后，可进一步由梯度场重建折射率场，当平面波在其中传播时，对应即为波前信息，需要说明的是，本文所重构的波前指的是光程差场，或者说折射率场，并不涉及波长。图像重建常用方法有求解泊松方程、滤波反投影重建、希尔伯特变换等，但这些方法都会出现误差大精度小的问题。根据已知波前梯度点和待测波前折射率点的相对位置构建Southwell数学模型，即假设相邻两点的折射率差与这两点波前梯度测量值的算术平均值相等，对于每个点的折射率，可利用其周围点进行求解。求解波前的矩阵方程为

式中，X列向量是待求波前，S列向量是已知波前梯度，A是根据Southwell模型构造的稀疏矩阵。方程求解有多种方法，如直接求逆法、高斯消元法、快速傅里叶变换算法、迭代法等，其中反对称偏导积分（Antisymmetric Partial Derivative Integral，ASDI）法是基于傅里叶变换的一种，首先构建所测斜率与波前真实斜率的最小二乘误差模型，将空域中的积分运算映射为频域中一组傅里叶基函数的线性组合，然后将原先的梯度矩阵填充扩展至2倍，进而求取最优解［20］；Guass-Seidl（G-S）迭代法是给定一个初始折射率值，代入方程计算作为下次迭代的初始值，每计算一个折射率后，便将它更新为该点折射率值，并带入计算周围点的折射率，如此循环直至达到收敛条件。

通过数值模拟验证上述两种算法精度，取非周期性函数W1和周期性函数W2，计算两函数沿x，y方向的梯度数据，并分别用ASDI和GS算法重构原函数，原始函数和重构函数分别如图5和图6所示。

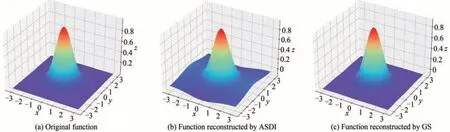
图5 非周期性原始函数及重构函数Fig.5 Aperiodic original and reconstructed function

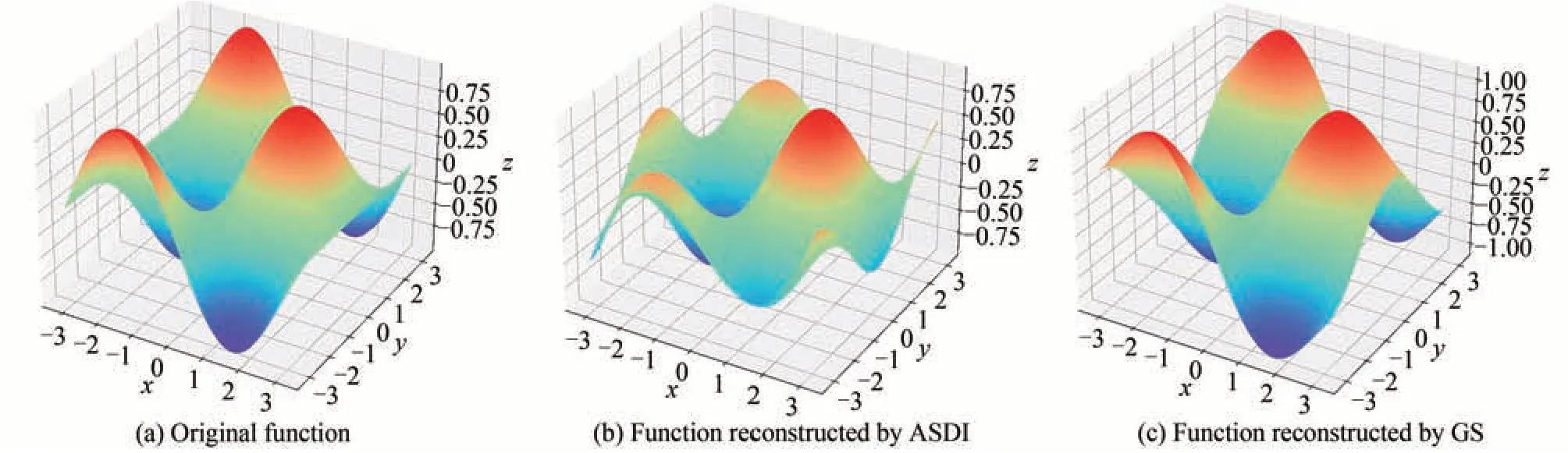
图6 周期性原始函数及重构函数Fig.6 Periodic original and reconstructed function

对原始函数和重构函数进行分析比较，用均方根误差RMSE（Root Mean Square Error，RMSE）表示算法重构精度。表2为两个函数分别在两种重构算法下的重构时间以及原始和重构函数间的RMSE，可知，ASDI法运算速度较快，但重构效果较差，尤其在边缘处重构精度偏低，GS迭代法运算速度虽然较慢，但是重构效果更好，在非周期函数中，重构函数与原始函数的RMSE不足0.05，且当初始给定条件接近真实情况时，运算速度可以加快，所以在实时处理时可以考虑用ASDI法，而在后处理时用GS迭代法。

表2 函数重构的时间及原始和重构函数的均方根误差Table 2 The time of function restructing and the RMSE between original and reconstructed function

4 流场探测实验

4.1 温压场实验

在实验室内搭建一套完整的背景纹影系统如图7所示，为了减少空调、人员走动等产生的气流对实验造成的影响，提前一天关闭空调和门窗，使实验室温度气流达到稳定。将打印的散斑图片用磁条固定在平滑的磁吸板上作为背景，既能实现固定也方便移动；将能产生明亮而稳定的火焰的便携式铝制酒精灯放置在距离磁吸板0.2 m处的稳定试验台上，火焰上方空气因受热会产生不均匀折射率场；实验所用160万像素的海康MA-CA016-10UM相机，像元尺寸为3.45 μm×3.45 μm，最大帧频249.1 fps，搭配适马150～600 mm镜头固定在距离磁吸板4m处的可调节三脚架上，USB连接电脑和相机组成实时成像采集系统，通过控制电脑即可控制相机，避免了采集图案或视频时出现抖动；为了减少不稳定光照对背景参数的影响，在磁吸板右前方放置一台880 W大功率LED打光灯，调节光束大小使背景全覆盖；调整三脚架高度使镜头、背景处于酒精灯火焰口上方30 cm处的同一直线上，调节镜头焦距保证对焦在背景中火焰上方气流扰动区域；分别在酒精灯点燃前和点燃后火焰状况达到稳定时采集视频，对视频进行后处理，读取全部帧，将燃烧前后的图像帧进行光流和波前计算并可视化。

图7 室内酒精灯燃烧实验场景图Fig.7 Scene diagram of indoor alcohol lamp combustion experiment

图8分别是酒精灯燃烧时火焰上方气流在均值窗口为5，20，50个像素下的二维光流图和三维波前图。图8（a）中平均光程差为41.56 μm，位移不明显，波前在边缘处不均匀，说明有较多的噪声，图8（b）中平均光程差为40.63 μm，在火焰上方有明显的不均匀气流，可以看出波前除中轴外较为均匀，图（c）中平均光程差为33.71 μm，光程差相比前两者有所减小，整体过度平滑、气流运动的细节丢失。因此，在酒精灯燃烧实验中，均值窗口在20个像素左右最合适。由2.1可知，光程差是折射率沿光传播路径的二维积分，光程差变化即为折射率变化，且在图中可以看出，正对于火焰上方的温度最高，光程差起伏也最为明显，而偏离火焰中轴处温度较低，光程差起伏也较弱。由此证明，室内酒精燃烧实验中，温度起伏与光程差起伏成正比，酒精燃烧的温度变化使得正对于火焰上方的空气折射率出现起伏，进而产生了明显的光程差变化。

图8 温压场的光流图和波前Fig.8 Optical flow image and wavefront of temperature pressure field

4.2 声压场实验

选择一个晴朗无风的天气在安静的园区内开展实验，园区内环境噪声不超过20 dB。实验所用相机为KAYA JETCAM-19高速相机，像元尺寸为10 μm×10 μm，最大帧频2400 fps，搭配尼康800 mm定焦镜头固定在稳定且高度可调的三脚架上，采集卡、光纤分别连接电脑和相机组成实时成像采集系统。使用常见的工业氧气和液化气，通过智能控制系统控制电子炮筒精确点火，发出最高160 dB的炮声。搭建室外背景纹影系统，以软件和镜头所在位置为原点，炮筒在离原点约100 m处，选用300 m左右处的树林作为不均匀背景，调节镜头使相机、炮筒口、背景处于同一直线上，为准确观察炮筒发射时的周围场况又不影响背景，调整镜头俯仰角保证炮筒口既出现在画面中又不占过多面积，调整相机参数保证相机准确对焦在自然背景上。在炮筒发射前5 s即点击鼠标开始采集视频，智能控制炮筒定时发射，一直到发射完毕后10 s停止采集，视频采样帧率为1000 Hz。对视频进行后处理，播放帧率为20帧/s，共300帧，读取全部帧，将每一帧图像与其相隔一帧的图像进行位移和波前计算并可视化。

图9 室外炮筒发射实验场景及布局Fig.9 Scene and layout of outdoor barrel launch experiment

如图10所示，从左往右，自上而下分别为炮筒发射不同时刻的背景图像以及均值窗口为50个像素时对应的光流场和波前。图10（a）是炮筒发射前0.1 s的观测场，可以看到背景图和光流场均无任何变化，波前平均光程差为0.34 μm，整体较平稳，说明周围环境未对观测场产生扰动，这是实验准确开展的前提；图10（b）是发射瞬间的观测场，背景图中的炮筒口还未有变化，而光流场中已经显示周围有清晰明亮的光流团，波前也发生跃变，最大光程差为140 μm，这说明发射瞬间炮筒口附近场因冲击发生了强烈的位移；图10（b）～（f）是发射后短时间内观测场的变化，可以看到背景图中只有炮筒口附近有烟尘粒子在移动，画面其他位置无变化，光流图中出现了以炮筒口为中心向周围场迅速传播的弧形光流，波前出现不断波动的光程差场，且随着传播距离的增大，波峰逐渐降低，以出现的前两列波为例，第一列波如图10（c）～（e）所示，对应最大光程差为200 μm左右，第二列波如图10（d）～（f）所示，对应最大光程差为150 μm左右，两列波由炮筒口传播至观测场中间再到观测场最右边，传播时间0.2 s，传播对应的实际距离有60 m，传播的波场速度约等于声速。已知声压是由于物体振动引起空气疏密起伏从而在原来大气压强下叠加的变化压强，由此证明，外场炮筒引爆实验中发生了声波的传播，炮筒粒子冲击瞬间发出的高分贝声音使得周围总大气压强发生变化，进而使大气折射率出现起伏，产生了明显的光程差变化。

图10 声压场的自然背景、光流图像和波前Fig.10 Natural background，optical flow image and wavefront of voice pressure field

5 结论

本文介绍了背景纹影技术流场探测的原理和可行性，从原理出发分别研究了BOS技术中位移检测和波前重构两大部分，包括实现方法和精度测试。发现：1）位移检测中，Farneback光流算法效果最好，但是其算法参数以及背景参数都会影响检测精度，理想情况下，检出的最小位移量可达1/400个像元；2）波前重构中，基于傅里叶变换的ASDI法速度较快但是精度较低，GS迭代法的速度较慢但是精度较高，对于非周期函数，重构函数和原始函数的RMSE不足0.05，当对速度要求较高时可选用ASDI法，而当对精度要求较高时可采用GS迭代法。其次将搭建的BOS技术流场测试系统用于实验室内和外场两种典型流场环境中，均可实现定性观察和定量测量。高精度背景纹影系统装置简单、算法成熟，除本文所示温压场和声压场两种流场外，BOS技术得到的折射率还可用于热场或密度场的温度和密度计算，所提取的波前信息也有助于进一步了解流场结构，在自适应光学、目标探测等科研方面以及精密仪器检测、发动机性能提升、气动外形优化等工业领域都具有广泛的应用前景。