电流调制下光注入VCSEL-SA的可重构逻辑运算

肖路遥，唐曦，林晓东，高子叶，段志飞，杜潇睿，夏光琼，吴正茂，邓涛

（1 西南大学 物理科学与技术学院，重庆 400715）（2 微纳结构光电子学重庆市重点实验室，重庆 400715）

0 引言

随着社会的迅猛发展，人工智能、互联网、多媒体、5G通信、大数据业务等现代科技技术已经广泛应用于国民生产生活，全社会对算力的需求以每年至少20%的速度递增，由此对计算系统的算力提出了前所未有的挑战。目前，我国的“神威-太湖之光”超级计算机的峰值计算能力可以达到12.5亿亿次/秒。然而，这种传统的存算分离的冯诺依曼架构在存储、运算速率、功耗等方面的瓶颈限制了其进一步发展。此外，沿用至今的“摩尔定律”也因CMOS工艺的限制而遭遇瓶颈，集成电路的发展已进入后摩尔时代。在此背景下，人工神经网络的研究与发展备受关注，基于硅基电子器件或光学器件的光子神经网络已经变成了该领域的焦点问题。光子神经网络在处理复杂的人工智能任务时具有较低的功耗和高速率的优势，可克服冯诺依曼架构的局限，因而可以提供一种新的可行性方案用于解决诸如决策、深度学习和优化、模式识别以及感知信息处理等更复杂的计算任务。近年来，光子神经网络因其在速度和能量效率方面明显优于传统电子方法而成为研究热点［1-5］。迄今为止，神经形态光子器件的研究引起了科研工作者的广泛关注，例如光子晶体结构［6］，共振隧穿二极管光电探测器［7］，光纤激光器［8］，半导体光放大器［9］，光学调制器［10］和半导体激光器［11-16］等。在这些神经形态光子器件中，半导体激光器具有与生物神经元相似的多种行为，且可以产生比生物神经快达8个数量级的脉冲响应，因而可作为一种理想的人工神经元。目前，不同类型的半导体激光器已经在神经形态计算系统中得到了广泛研究和应用，如微盘激光器［11］，微柱激光器［12］，微环激光器［13］，量子点激光器［14］，带有饱和吸收体的激光器［15］和垂直腔面发射激光器（Vertical-Cavity Surface-Emitting Lasers，VCSELs）［16-17］。特别地，VCSEL具有体积小、功耗低、成本低以及与光纤耦合效率高等优点［18-19］，因此，探索VCSEL器件的非线性动力学行为及其在神经拟态计算相关领域的应用可望推动人工智能领域的创新发展。最近，外部刺激下VCSEL光子神经元的spiking动力学行为已经被理论和实验报道［20-23］。值得注意的是，在VCSEL中引入饱和吸收体后，可以构建两段式可激发激光器（VCSEL-SA）。与传统的光子神经元模型相比，这种集成的光子神经元类似于LIF模型，其输出的spike信号可携带时空信息，能更好的模拟生物神经元的特性，且能够激发更短的亚纳秒光脉冲，其兴奋阈值也可在一定范围内灵活控制［24-27］。因此，VCSEL-SA在光子神经网络相关领域的研究和应用具有巨大的价值。

光学逻辑门作为光网络系统中的基本单元，在光交换、光提取、光计算等复杂的光信息处理任务中起着关键性作用［28］。PERRONE S等基于光注入VCSEL，利用噪声和偏振双稳的相互作用实现了随机逻辑门［29］，许葛亮等利用外部光反馈注入VCSEL实现了可重构光电混沌逻辑门［30］，钟东洲等基于外部光注入VCSEL实现了光电复合逻辑门［31］，项水英等基于光注入VCSEL-SA，通过控制抑制窗口进一步实现了全光异或逻辑门［32］并基于监督学习算法训练的多层脉冲神经网络完成了XOR分类任务［33］。上述研究证实了利用VCSEL器件实现逻辑运算的可能性。因此探究基于VCSEL的逻辑运算架构及其逻辑运算性能对基于VCSEL的光子神经网络构建及其应用有着重要的意义。此外，考虑到可重构的逻辑器件可大大降低未来大规模光子集成的成本，提高逻辑器件的利用效率。本文提出了基于电流调制和光注入共同作用下的VCSEL-SA实现可重构光电逻辑门（NOT，NAND，NOR，XOR）的方案，数值分析了影响逻辑门运算性能的主要因素，并讨论了不同逻辑门实现重构的条件。

1 系统模型与理论

图1是基于电流调制下光注入VCSEL-SA的光电逻辑门（NOT，NAND，NOR，XOR）系统结构图。其中，VCSEL-SA的偏置电流略小于阈值电流以避免激光器处于自脉冲振荡状态［34］。矩形脉冲信号O通过马赫-曾德尔调制器（Mach-Zehnder Modulator，MZM）后注入VCSEL-SA可以使其成功激发一个spike。在此基础上，将任意波形发生器生成的矩形脉冲电信号A和B通过反相器（Inverter）实现反相，再经偏置器（Bias Tee）与直流偏置耦合后注入到VCSEL-SA，通过合理设置调制电流大小即可实现可重构的光电逻辑门（NOT，NAND，NOR）。另外，移除红色虚线框内的调制器和反相器后，即电信号A作为兴奋信号输入VCSEL-SA，而电信号B通过反相器实现反相后作为抑制信号输入VCSEL-SA，且此时无光注入信号，通过选取合适的偏置电流以及调制信号幅度，VCSEL-SA可以实现XOR逻辑运算。在所有的逻辑运算中，当VCAEL-SA激发spike时，逻辑运算结果为1，否则为0。

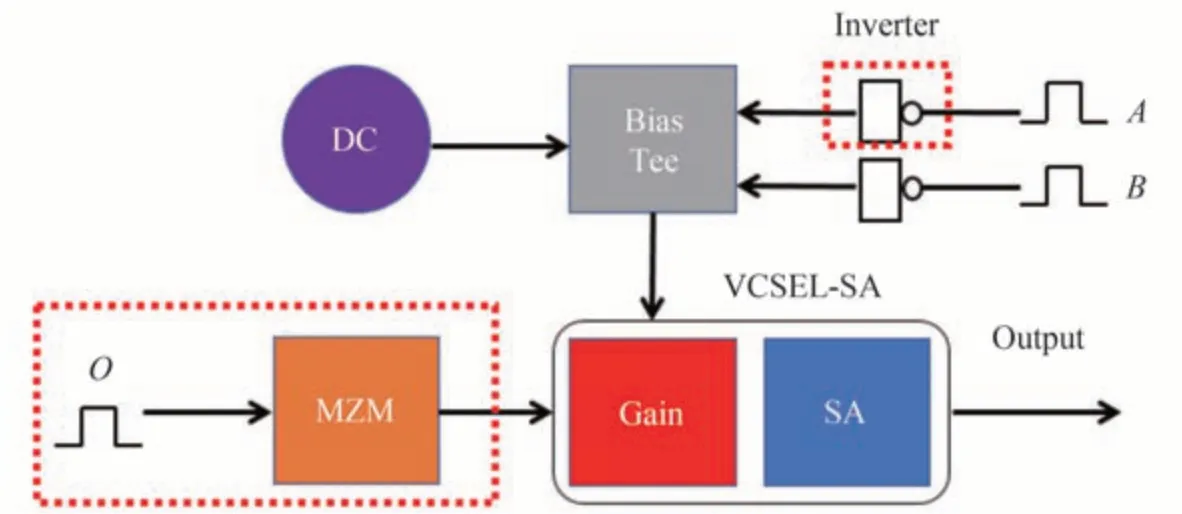
图1 基于VCSEL-SA的光电逻辑门（NOT，NAND，NOR，XOR）的系统结构图Fig.1 Schematic diagram of photoelectric logic gate（NOT，NAND，NOR，XOR）based on VCSEL-SA

考虑到电流调制和光注入的影响并忽略偏振效应，基于VCSEL-SA的逻辑运算可以用修正的Yamada模型来描述，其速率方程表示为［15，35］

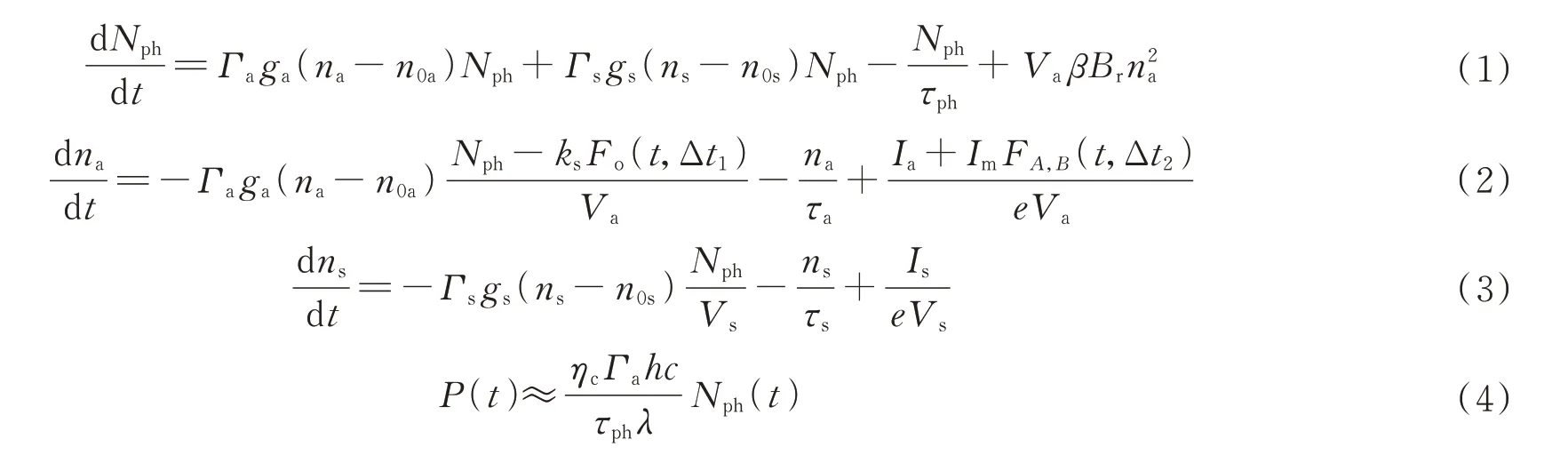
式中，下标a和s分别表示增益区和饱和吸收区，Nph(t)表示腔内总的光子数，P(t)是激光器的输出功率，n(t)是载流子数，I是偏置电流。ksFO(t，Δt1)代表耦合到激光器增益区的光信号，ImFA，B(t，Δt2)代表调制信号，其中ks是注入强度，Im是调制信号的幅度，Δt1和Δt2分别表示光信号和电信号的扰动时间。VCSEL-SA的其他参数如表1所示，使用四阶龙格库塔法数值求解上述方程。

表1 VCSEL-SA的参数值Table 1 Typical VCSEL-SA parameters

2 结果与讨论

2.1 电流调制下VCSEL-SA的spiking动力学特性

图2给出了无光注入时VCSEL-SA在不同调制电流下的输出情况，其中，Ia=2.3 mA，Δt2=1 ns，Im分别为1.5、4.5、7.5、15、30 mA。随着Im的增加，VCSEL-SA输出的spikes数目逐渐增多，且其峰值功率也逐渐增大，spike间隔越小，这种现象类似于生物神经元激发的tonic脉冲。当Im到达15 mA时，VCSEL-SA输出呈现明显的振荡过程。当Im继续增加到30 mA时，VCSEL-SA首先会激发出一个大功率spike，随后经过短暂的振荡过程快速进入稳定输出态，这与生物神经元输出的phasic脉冲相似，这些结果与光注入VCSELSA的spiking动力学行为基本一致［38］。

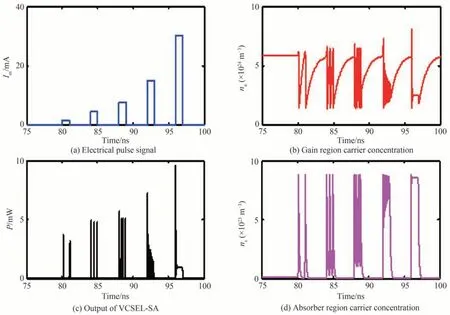
图2 不同的调制信号幅度下VCSEL-SA的输出情况Fig.2 The output of the VCSEL-SA for different modulation signal amplitude

图3给出了无光注入且调制信号扰动时长Δt2变化时VCSEL-SA输出的情况，其中，Ia=2.3 mA，Im=1.5 mA，扰动时长依次为1、2、4 ns。从图中可以看出，随着Δt2的增加，VCSEL-SA激发的spike数目逐渐增多，说明spike激发的数量与扰动时长Δt2有关，这为实现VCSEL-SA的spike编码和逻辑运算提供了又一种调控手段。

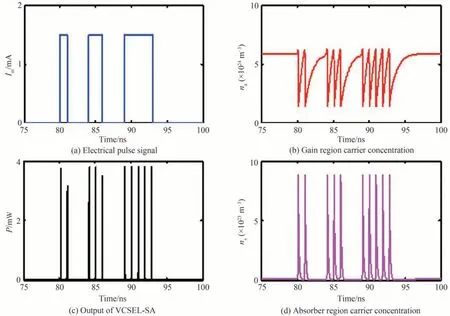
图3 不同调制信号扰动时间对应的VCSEL-SA输出Fig.3 The output of the VCSEL-SA for modulation signals with different perturbation durations

为了进一步探究外部调制电流信号对光注入VCSEL-SA激发的spike信号进行抑制的影响。图4给出了光注入VCSEL-SA在无电流调制和增加电流调制时的输出情况，其中，光注入强度ks=3×103，扰动时长Δt1=15 ns，偏置电流Ia=2.3 mA。在没有调制信号输入的情况下，光注入VCSEL-SA可以输出连续的spike信号，如图4（c）所示。此时，输入一个负脉冲电信号（Im=1.5 mA，Δt2=5 ns）对VCSEL-SA进行调制，在脉冲作用区输出的spikes信号被完全抑制，如图4（d）所示。这可以解释为输入的负脉冲抑制信号使得激光器增益区载流子的积累难以达到VCSEL-SA的兴奋阈值，从而无法激发spike。由此可见，通过控制光注入和电调制信号，VCSEL-SA可以灵活的激发spike信号或者抑制输出的spike信号，这种控制spike激发或抑制的方式可用于设计基于VCSEL-SA的光电混合型逻辑电路（NOT，NAND，NOR，XOR）。

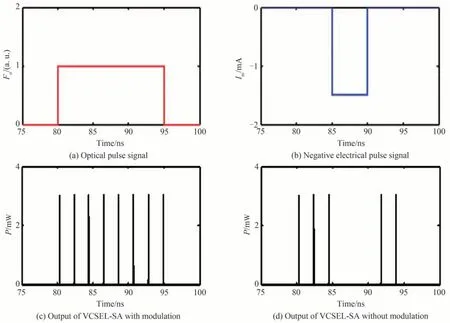
图4外部扰动下VCSEL-SA的输出情况Fig.4 Output of VCSEL-SA under external disturbance

2.2 光电逻辑门（NOT，NAND，NOR，XOR）的实现

图5 给出了光注入VCSEL-SA实现NOT门逻辑运算的情况。本节中，在未做特别说明的情况下，固定偏置电流Ia=2.3 mA，光注入强度ks=3×103，扰动时长Δt1=1 ns。在每一个光脉冲注入下，VCSEL-SA可成功激发一个spike信号，如图5（b）所示。此时，通过反相器对电流调制信号A（B）进行反相，然后通过偏置器注入VCSEL-SA，对应的调制信号幅度Im依次为0 mA，0.2 mA，0.5 mA，1 mA，如图5（c）所示。从图5（d）可以看出，当反相的电流调制信号较小时，VCSEL-SA在光脉冲的作用下仍然可以激发spike信号。随着电流调制信号的增大，VCSEL-SA有源区内累积的载流子数减小，无法满足spike激发的阈值条件，因而不再激发spike信号。由此可见，通过控制调制信号的强度，可以使VCSEL-SA实现NOT门的逻辑运算。

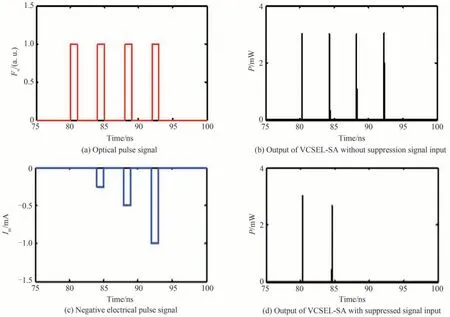
图5 NOT门逻辑运算的实现Fig.5 Implementation of NOT logic operation

图6给出了VCSEL-SA实现光电逻辑门（NAND，NOR）的情况。在与非门（NAND）逻辑运算中，两路调制电流幅度均设定为0.3 mA，两路电信号经过反相器反相后分别输出0011和0101，如图6（b）和（c）所示。从图6（d）可以看出，两路输入的电信号只要存在“0”，VCSEL-SA则可以激发spike信号。当两路电信号均输出“1”时，VCSEL-SA有源区的载流子无法达到激发阈值条件，因而不再能激发spike信号。对于或非门（NOR）逻辑运算，两路电信号分别输出0011和0101，其调制电流幅度均设定为1 mA，如图6（f）和（g）所示。从图6（h）可以看出，两路输入的电信号只要存在“1”，VCSEL-SA有源区的载流子则无法达到激发阈值条件，此时不再有spike信号被激发。仅仅当两路电信号均输出“0”时，VCSEL-SA可以激发spike信号。值得注意的是，调制电流大小的选择与光注入强度及VCSEL-SA的偏置电流大小有关，因此，对于光注入VCSEL-SA，通过合理选择调制电流的强度，VCSEL-SA可以实现光电逻辑门（NAND，NOR）的逻辑运算功能。

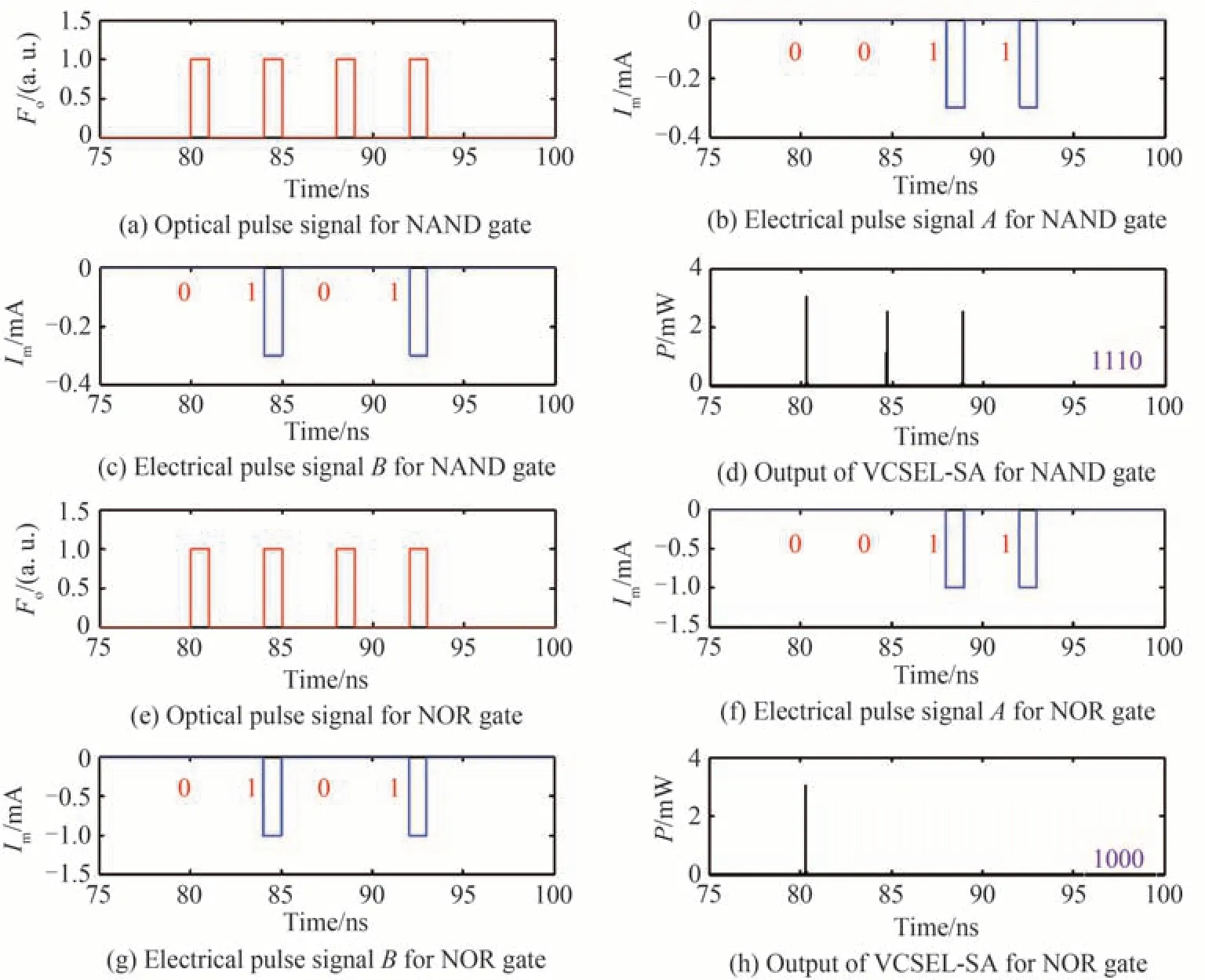
图6 NAND门和NOR门的逻辑运算实现Fig.6 Logic operation implementation of NAND gate and NOR gate

图7 给出了实现光电逻辑门（XOR）的情况。在执行XOR逻辑运算时，外部光注入信号不再需要，第一路调制信号的反相器需要移除且需对两路调制电流信号进行处理。通过数字信号处理技术把A和B两路信号的每一位码元转换为原码后并补加上其取反的码元，即“0”转换为“01”，“1”转换为“10”，图7（a）和（b）分别表示处理过后的A、B两路信号，其中蓝色实线是原信号，红色实线是补加的信号。经过处理后的A（′01′′01′′10′′10′）和B（′01′′10′′01′′10′）两路调制电信号同时注入VCSEL-SA，XOR逻辑运算的结果如图7（c）所示。值得注意的是，与光电逻辑门（NAND，NOR，NOT）相比，XOR逻辑操作的实现不需要光信号的注入，仅仅需要改变电流调制信号的输入方式，即调制信号需要增加相应的码元且调制信号A无需反相。由此可见，通过控制光注入信号、直流偏置及调制信号的输入方式即可使该系统实现不同逻辑运算功能的转换，从而实现逻辑门的重构。需要指出的是，为了直观地表征系统的逻辑运算功能，在模拟过程中相邻扰动信号的时间间隔设定为5 ns，且这个时间在一定的范围内可调。在实际应用中，这个时间间隔会受到偏置电流、光注入强度等参数的影响，本质上由神经元的不应期决定。

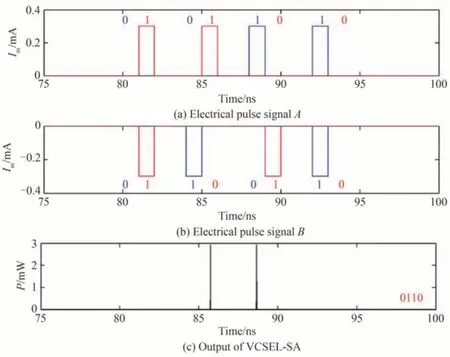
图7 XOR逻辑运算的实现Fig.7 Implementation of XOR logic operation

为了进一步探究光电逻辑门实现重构的优化工作参数范围，图8以逻辑门（NAND，NOR）为例给出了不同调制电流下VCSEL-SA输出的演变图谱，其中，Ia=2.3 mA，ks=3×103，光注入脉冲和电流调制信号的扰动时长分别为Δt1=1 ns，Δt2=1 ns。当两个电流调制信号（10）和（01）分别注入VCSEL-SA，且电流调制强度Im小于0.32 mA时，spike能够被激发，满足NAND的实现条件，而当电流调制强度Im大于0.32 mA后，spike不再被激发，满足NOR的实现条件，如图8（a）所示。当两个相同模式（11）的电信号调制VCSEL-SA，且电流调制强度Im大于0.18 mA时，VCSEL-SA不能激发spike信号，满足NAND和NOR的实现条件。综合图8（a）和（b）可以看出，当调制信号幅度Im的取值范围在0.18～0.32 mA时，NAND能够被实现，当调制电流大小Im大于0.32 mA时，NOR能够被实现。因此，对于给定的光注入VCSEL-SA，我们通过调节调制电流信号的幅度可以实现NAND和NOR逻辑运算功能的转换，即实现NAND和NOR逻辑门的重构。

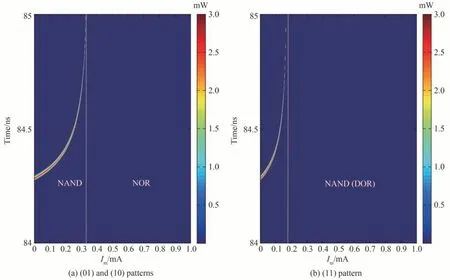
图8 VCSEL-SA的输出随调制幅度Im变化的演变图Fig.8 Evolution of the VCSEL-SA′s output with Im

图9进一步给出了两路调制电流信号的输入延时对光电逻辑门（NAND，NOR）的影响，这里只讨论了当两个调制信号输入非“0”信号的情况，即输入模式为11。两路电信号均通过反相器反相，且第一个调制信号的下降沿到第二个调制信号的下降沿的时间距离为Δτ。图9（c）～（d）和图9（g）～（h）是NAND门运算的情况。当调制电流大小Im=0.2 mA时，随着Δτ从0 ns逐渐增加，VCSEL-SA开始无法激发spike信号，即可以实现NAND操作。当输入延时Δτ达到0.3 ns时，VCSEL-SA激发了spike信号，此时NAND逻辑操作失效，如图9（d）所示，这主要是因为当输入的两路电信号的时延达到一定程度后，调制信号无法使VCSELSA有源区内的载流子累积的水平降低到阈值以下，因此VCSEL-SA仍然能激发一个spike。当调制电流被增加到Im=0.3 mA时，类似的结果仍然可以被获得，如图9（g）和（h）所示。图9（k）～（l）和图9（o）～（p）是NOR门运算的情况，调制电流幅度分别为0.5 mA和1 mA。从图9（i）～（p）可以看出，对于两个大小不同的调制信号，即使两路电信号的输入延时Δτ大于调制信号的扰动时长Δt=1 ns，NOR逻辑运算仍然可以实现。这主要是因为单路调制电流的幅度已经足够抑制激光器的spike输出，这与图6（e）～（h）中NOR门运算的情况一致。由此可见，本文提出的可重构逻辑门在两路调制信号存在一定的输入延时也可实现NAND和NOR逻辑运算。当调制信号幅度达到一定值后，信号间的输入延时对逻辑运算（NAND、NOR）的影响相对较小，这主要是因为大的调制信号注入可以使增益区的载流子浓度急速下降，能更加有效地抑制VCSELSA的spike激发，因而可以容许更大的输入延时范围。需要指出的是，实现逻辑运算所能容许的输入延时范围受探测光O的注入强度、偏置电流大小和调制电流大小的影响，因此，在实际的逻辑运算中，需要合理的设置光注入强度、VCSEL-SA偏置电流、调制信号的幅度及两路调制信号之间的时延。

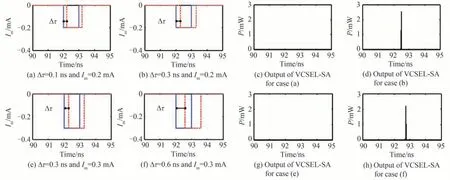
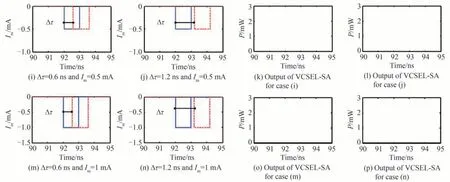
图9 两个电流调制信号之间的输入延时对光电逻辑门（NAND，NOR）的影响Fig.9 Influence of the input delay between two current modulation signals on the optoelectronic logic gate（NAND，NOR）

在逻辑电路的实际应用中，噪声不可避免地会对系统的性能产生影响。为了进一步分析噪声对本文提出的可重构逻辑运算电路的影响，图10（a）～（c）和图10（d）～（f）分别给出了信噪比SNR为20 dB和10 dB时，光电逻辑门（NAND，NOR，XOR）输出的结果，其中，Ia=2.3 mA，ks=3×103，光注入脉冲和电流调制信号的扰动时长均为1 ns。当调制信号幅度Im=0.3 mA时，对比图10（a）和图10（d），当信噪比从20 dB下降到10 dB时，NAND的逻辑运算失效。图10（b）和（e）是调制信号幅度Im为0.5 mA时，NOR逻辑操作的输出情况，可以看出即使在较大的噪声影响下，NOR门仍然可以实现。图10（c）和（f）是在调制信号幅度Im=0.3 mA的条件下，XOR的输出情况，蓝色实线是原信号，红色实线是补加的信号。从图中可以看出，较大的噪声下XOR逻辑运算仍然可以实现。显然，虽相对于NAND逻辑运算而言，NOR和XOR逻辑运算对噪声的容忍性较好。由此可见，虽然噪声对逻辑门的运算性能有一定的影响，但本文提出的基于电流调制下光注入VCSEL-SA的逻辑电路对噪声有一定的容忍性。

图10 噪声对光电逻辑门（NAND，NOR，XOR）实现的影响Fig.10 The effect of noise on the implementation of optoelectronic logic gates（NAND，NOR，XOR）

3 结论

基于电流调制和光注入共同作用下带有饱和吸收体的垂直腔面发射激光器（VCSEL-SA）的spiking动力学特性，提出了一种可重构的光电逻辑门（NOT，NAND，NOR，XOR）设计方案，并数值分析了系统的逻辑运算特性。结果表明，选取合适的调制电流大小可以实现NAND和NOR逻辑门的重构。两个电流调制信号之间的延时对光电逻辑门（NAND，NOR）的实现几乎没有影响。通过改变外部调制电流信号的输入方式并去掉光注入信号，可以实现XOR逻辑运算。此外，研究进一步证实，在一定的条件下，本文提出的基于VCSEL-SA的光电逻辑门对噪声具有一定的容忍性。本文所设计的逻辑运算电路有望对未来超高速、大带宽的光子神经网络应用于相关领域所需基本逻辑运算元器件的开发设计提供一定的理论基础。