基于压力拱理论的极软岩隧洞衬砌应力变形研究

黄旭斌，苗 喆， 陆 希，张 凯，邓立文，张华毅

(1. 中国电建集团西北勘测设计研究院有限公司，西安 710065；2. 中国电建集团西北勘测设计研究院有限公司 博士后科研工作站，西安 710065；3. 河海大学，南京 210024)

0 前 言

为了促进“双碳目标”的顺利推进，中国将有一大批抽水蓄能电站即将开工建设。伴随着大量的输水隧洞工程施工，将面临极软破碎围岩等不良地质条件问题[1-3]，给隧洞工程设计与施工带来极大不便，甚至在开挖过程中会出现围岩失稳坍塌，造成经济损失甚至人员伤亡。隧洞开挖过程中，随着临空面上应力的释放，围岩的应力场将发生重分布，形成新的应力场[4]。对于极软岩而言，隧洞开挖后自洞壁向围岩深部依次形成围岩松动区-压力拱区-原岩应力区[5-6]，且随着施工时间持续，将会形成动态压力拱[7]。台启民等[8]通过数值模拟的方法，认为压力拱的演化规律分为3个阶段，即外边界形成阶段，内边界连通阶段，内、外边界发展阶段，且认为在第一阶段的时候采取适当的超前支护措施，以防止隧道周围松动区的连通。徐泽沛等[9]通过计算发现无衬砌隧洞开挖后，随着时间的发展，形成的压力拱的垂直外边界基本不变，垂直内边界逐渐减小，此处提及的内边界应为相关文献[6]中的松动圈外边界一致。极软岩隧洞开挖后，压力拱很有可能在短时间内形成，压力拱理论则认为压力拱内部围岩应力将全部作用在衬砌结构上。因此，压力拱理论是我国地下工程设计的力学基础[10]，对地下工程设计具有指导意义。

对于极软岩隧洞而言，不仅要关注隧洞开挖后的稳定性，还需保证隧洞在一衬甚至二衬后不被破坏。相关学者虽对围岩压力拱进行了研究，但对衬砌的安全性未做深入考究，现有研究成果对实际工程设计方案制订指导性不强。因此，本文基于压力拱理论，计算得到压力拱的计算边界，通过有限元计算方法分析作用在隧洞衬砌的内力和变形规律，为极软岩隧洞坍塌形成压力拱后的支护设计提供理论支撑。

1 工程概况

新疆哈密抽水蓄能电站通风兼安全洞采用城门洞形断面开挖，开挖宽度8.5 m，开挖高度8.25 m，具体体型如图1所示。极软破碎岩体隧洞总长约150 m，围岩类别为Ⅴ类，平均埋深约140 m。根据现场反馈，通风兼安全洞在进入极软破碎围岩段后由于支护不及时而出现了坍塌，隧洞压力拱已形成，因此很有必要对形成压力拱后隧洞衬砌的安全性进行验算。通风兼安全洞的支护方案为：① 顶拱采用超前大管棚注浆支护，等注浆层形成强度后进行开挖；② 进行一衬支护，包括喷锚支护和钢支撑支护；③ 进行二衬混凝土支护。

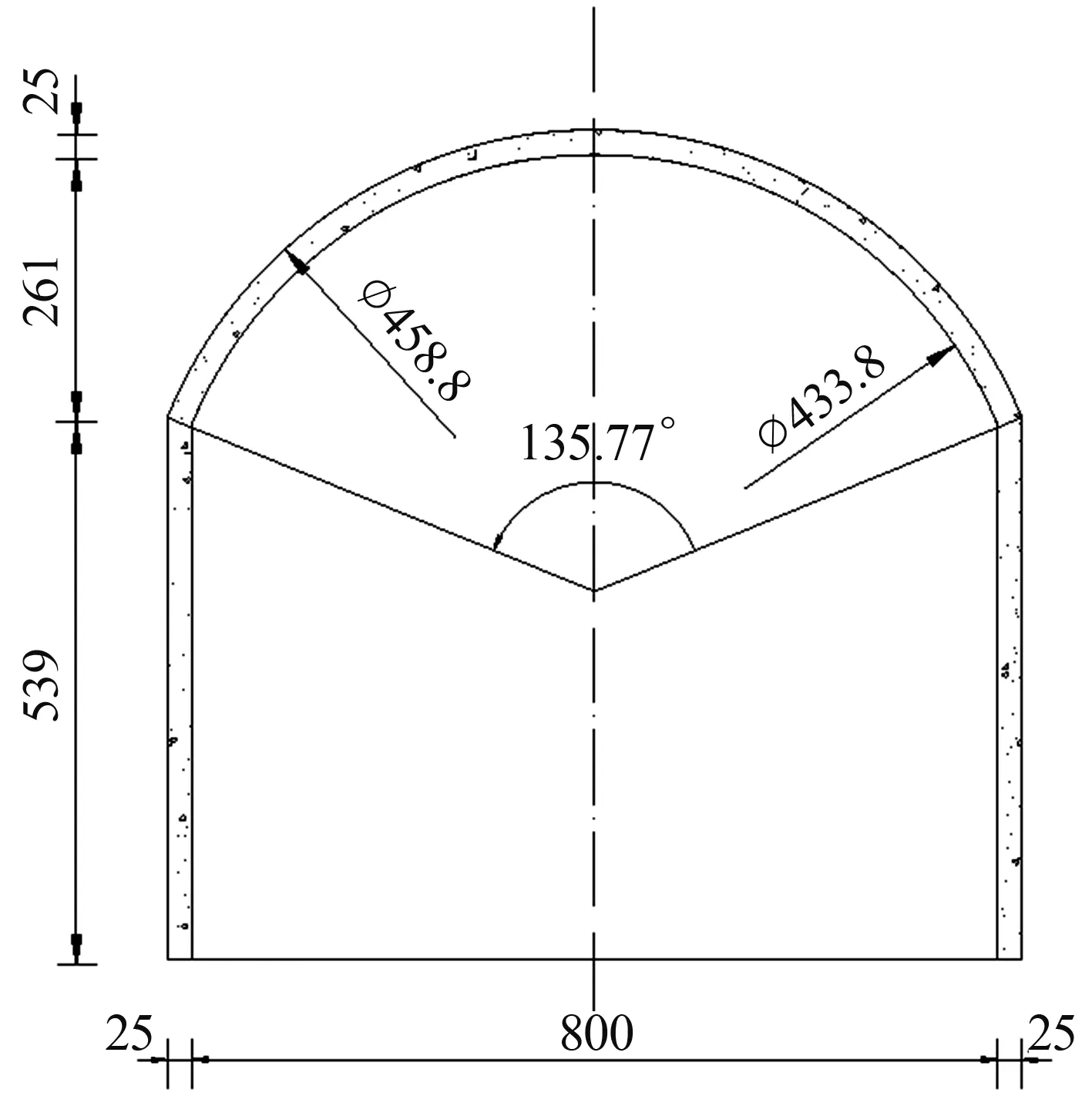
图1 通风兼安全洞体型 单位：cm

2 计算方法及参数选择

2.1 基本假定

假定隧洞压力拱已完全形成，压力拱内围岩压力将全部由一衬和二衬来承担，因此本文对计算工况进行如下假定：

(1) 假定隧洞一衬支护后停留时间较长，山岩压力直接作用在一衬上；

(2) 假定一衬支护完全破坏，山岩压力直接作用在二衬支护上，假定二衬厚度为0.5、0.8 m和1 m；

(3) 假定一衬后立即二衬支护，衬砌厚度为0.5 m。基于上述假定，对以上3种假定共5种工况进行衬砌结构在顶拱中心内侧、拱肩内侧和边墙中心内侧3个位置的应力和变形进行分析。

2.2 压力拱理论

压力拱是地下空间工程常见的一种现象，具有客观存在但肉眼无法观测到，不但存在于拱顶，还可能存在于两侧边墙，在无人为施加外边界荷载的情况下具有自我调节达到稳定等特点[8]。深埋隧洞压力拱形状为二次抛物线，拱最大宽度和拱高按照经验公式(1)和公式(2)确定：

(1)

(2)

公式(1)～(2)中：φ为内摩擦角，(°)；fk为岩石坚固系数(普氏系数)，本文计算中取0.5，其余参数意义如图2所示。

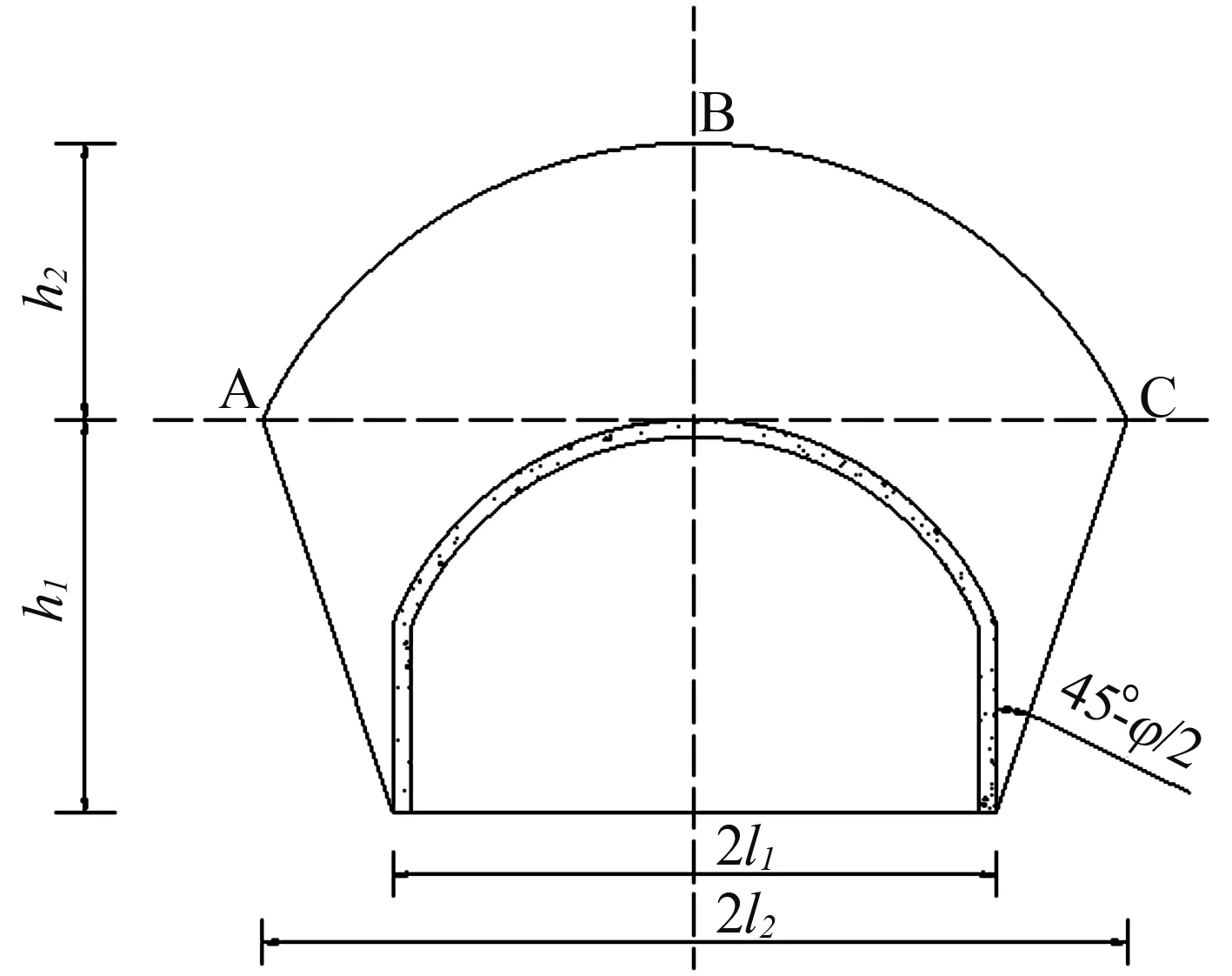
图2 深埋隧洞压力拱体型

在确定压力拱宽度l2和高度h2后，作用在顶拱和边墙上的最大山岩压力可通过公式(3)和公式(4)计算得到：

(3)

(4)

公式(3)～(4)中：qb为作用在压力拱的最大山岩压力,kN;qe1为作用在B点的水平向压力,kN;qe2为作用在边墙底部水平向压力。

2.3 数值模型建立及参数选取

哈密通风兼安全洞衬砌结构模型为三维有限元计算模型，采用数值模拟方法将压力拱理论计算得到的荷载施加到衬砌上，计算衬砌上的内力和变形。本次衬砌计算范围沿洞轴线方向长度为5 m，隧洞衬砌结构网格划分如图3所示。从外到内分别代表注浆加固层(0.5 m)、喷层混凝土(0.25 m)和二次衬砌(0.5、0.8 m和1 m)。计算时衬砌结构采用八节点三维单元模拟，钢支撑采用梁单元模拟。计算总单元数为1 370个，其中梁单元有220个；总节点数为1 881个。模型采用笛卡儿直角坐标系，其整体坐标系的X轴与通风兼安全洞的轴线一致；垂直方向为Z轴，向上为正，Y轴以右手法则确定，水平向左为正。

图3 隧洞衬砌结构网格划

根据现场调研及相关试验，坍塌段围岩参数如表1所示。一衬包括注浆层、喷层混凝土及钢支撑以及二衬混凝土均按照弹性材料进行计算，参数如表2所示。

表1 坍塌段围岩参数

表2 衬砌材料计算参数

3 结果与分析

3.1 衬砌主应力

(1) 仅一衬支护工况下主应力分析

在压力拱作用下，由于城门洞型衬砌的结构形式，发生应力较大地方可能出现在顶拱中心、拱肩和边墙中心等位置。大、小主应力主要表征作用在衬砌结构上的拉、压应力是否在材料的设计强度范围内。仅一衬支护工况下分别作用在注浆层和喷层混凝土上3个位置上的大、小主应力如图4所示，其中图4(a)为大主应力。图中正值表示拉应力，负值表示压应力。从图4(a)中可以看出，作用在注浆层顶拱和拱肩位置未出现拉应力，均为压应力。作用在喷层混凝土上3个位置的应力在数值上均大于相同位置注浆层的应力，主要是由于喷层混凝土的弹性模量更大。喷层混凝土上3个位置大主应力计算值均超过1.5 MPa，大小关系为边墙中心>拱顶中心>拱肩。

图4 仅一衬支护条件下衬砌各位置主应力

图4(b)为小主应力计算结果。从图中可以看出，作用在注浆层边墙中心的应力较顶拱中心和拱肩位置大一些。然而，对于喷层混凝土而言，作用在拱肩位置的应力最大，其次为边墙中心和顶拱中心。现有标准和文献对注浆层是否会发生破坏的研究较少，但对于喷层混凝土是否发生拉/压破坏，GB 50086-2015《岩土锚杆与喷射混凝土支护工程技术规范》[11]给出了C25喷层混凝土拉/压设计强度标准值，分别为1.27 MPa和11.4 MPa，从图4计算的结果可知，仅一衬支护条件下拱顶、拱肩和边墙均可能出现拉坏现象，但发生压坏的可能性较小。因此在实际施工过程中，不建议一衬支护停留过长时间，需及时进行二次支护，以防一衬发生破坏进一步导致围岩的失稳。

(2) 仅二衬支护工况下主应力分析

仅二衬时各位置主应力随衬砌后的变化规律如图5所示。其中大主应力随衬砌厚度的变化如图5(a)所示，从图中可以看出，各位置出现的大主应力均为正值，说明这些位置均出现了拉应力。在衬砌厚度一定时，作用在边墙中心的拉应力最大，其次为拱肩和拱顶中心。当衬砌厚度为0.5 m时，边墙中心的拉应力大于强度设计值，此处可能会发生拉坏现象，拱肩和顶拱中心拉应力小于强度设计值，这两处发生拉坏的可能性较小。对于其他两种厚度的二衬，拉应力均未超过强度设计值。随着衬砌厚度的增大，边墙中心的拉应力呈非线性减小，衬砌厚度从0.5 m增大至0.8 m，拉应力减小的幅度远大于衬砌厚度从0.8 m增大至1 m的幅度，拱肩和拱顶中心拉应力可近似为线性减小。

图5 仅二衬主应力随衬砌厚度变化规律

图5(b)为作用在二衬各位置小主应力随衬砌厚度变化规律。从图中可以看出，各位置出现的小主应力均为负值，说明这些位置均出现了压应力。从整体上来看，压应力随着衬砌厚度的增大呈减小趋势。不论衬砌厚度为多大，作用在拱肩位置的压应力均为最大。当衬砌厚度为0.5 m时，作用在边墙上的压应力大于作用在顶拱中心的压应力，当衬砌厚度大于等于0.8 m时，边墙中心和顶拱中心的压应力大小基本相同。再者，作用在二衬各位置的压应力均未超过强度设计值，因此各厚度下二衬出现压坏的可能性较小。

(3) 一衬和二衬联合支护工况下主应力分析

一衬和二衬联合支护工况下衬砌主应力如图6所示，其中图6(a)为各位置大主应力。从图中可以看出，作用在注浆层上的大主应力均为压应力，而作用在喷层混凝土和二衬上的大主应力为拉应力。在拱顶中心和拱肩位置，喷层混凝土的拉应力大于二衬上的拉应力，但在边墙上的规律相反。图中结果还表明，作用在3种支护上的拉应力均未超过强度设计值，因此不会出现拉裂现象。图6(b)为各位置小主应力。图中结果显示，作用在3种支护上的小主应力均为压应力，注浆层上的压应力最小，其次为二衬和喷层混凝土。作用在3种支护上的压应力均未超过强度设计值，因此出现压坏现象的可能性较小。

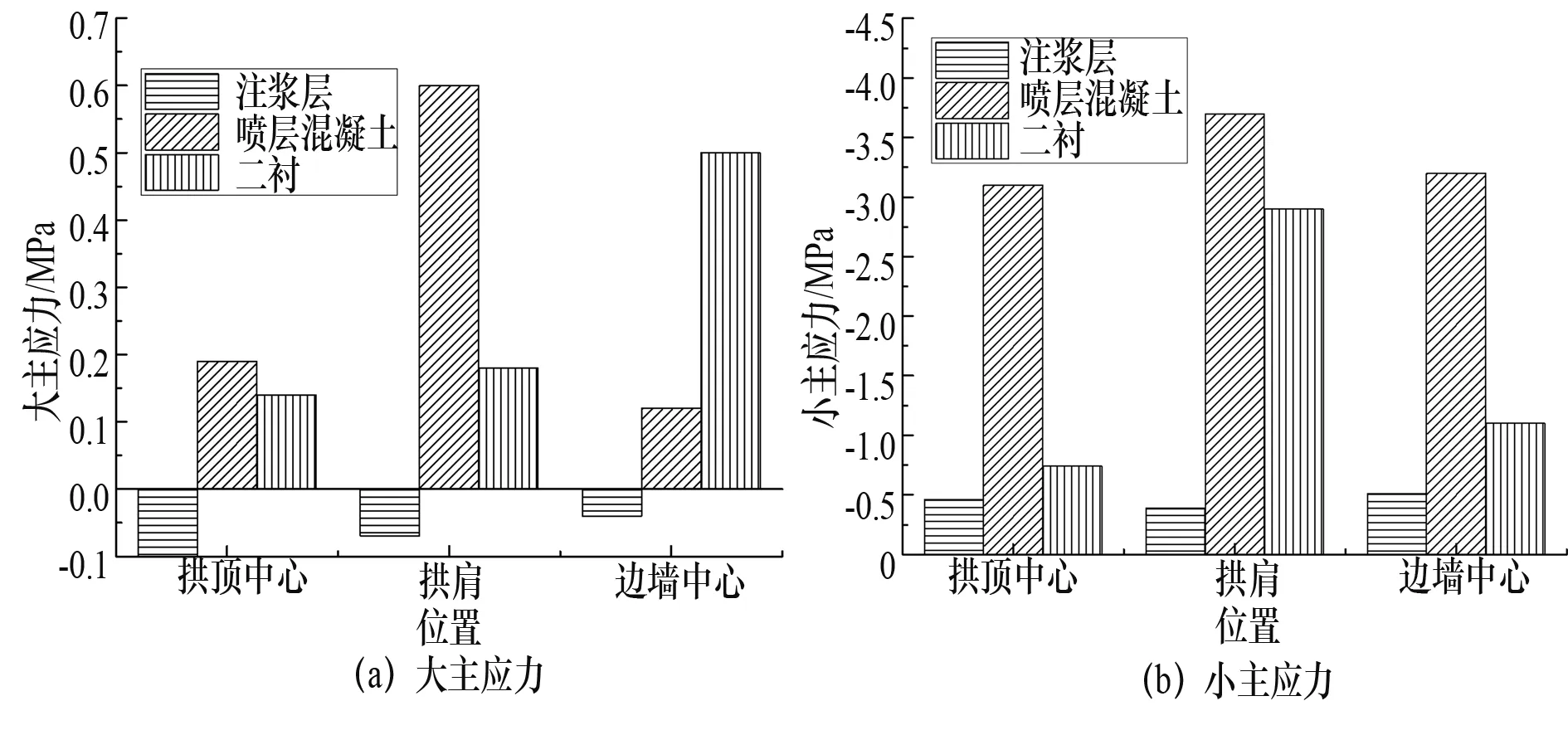
图6 一衬和二衬联合支护条件下衬砌各位置主应力

3.2 衬砌径向位移

(1) 仅一衬支护径向位移分析

仅一衬支护工况下注浆层和喷层混凝土径向位移如图7所示。从图7中可以看出，注浆层和喷层混凝土相同测点的径向位移大小差别较小，为协调变形。在本文计算得到的压力拱压力条件下，拱顶中心和边墙中心的径向位移大小相差较小，注浆层拱肩位置的径向位移稍大于喷层混凝土的径向位移。注浆层和喷层混凝土拱肩位置的径向位移较顶拱和边墙中心的径向位移小，主要是由于拱肩位于边墙和顶拱的交接位置，有一定的结构优势性。

图7 仅一衬支护工况下注浆层和喷层混凝土径向位移

(2) 仅二衬支护径向位移分析

仅二衬支护下各位置的径向位移随衬砌厚度的变化规律如图8所示。从图8中可以看出，在同一衬砌厚度工况下，顶拱中心的变形最大，其次为边墙中心，边墙中心的径向位移最小，主要是由于顶拱上作用的压力拱应力最大。各位置的径向位移随衬砌厚度的增大呈非线性减小趋势。

图8 仅二衬支护工况下衬砌径向位移

(3) 一衬和二衬联合支护工况下径向位移分析

一衬和二衬联合支护工况下各位置径向位移如图9所示。从图中可以看出，在联合支护的工况下，3种支护相应的位置位移差别较小，为协调变形。且拱顶中心的径向位移最大，其次为边墙中心和拱肩的径向位移，这与仅一衬工况下的径向变形规律有所差别，主要是由于二衬有底板，改变了整体结构，对边墙有一定的保护。

图9 一衬和二衬联合支护工况下衬砌径向位移

4 结 论

本文基于压力拱理论和数值模拟结合计算分析的方法，对仅一衬支护、仅二衬支护(厚度0.5、0.8m和1 m)和一衬与二衬联合支护等3种工况下拱顶中心内侧、拱肩内侧和边墙中心内侧等3个位置应力及变形进行分析，并得到如下结论：

(1) 经过计算发现，3种支护条件下衬砌压应力均未超过强度设计值，因此发生压坏的可能性较小，一衬和二衬(0.5 m)联合支护的方案是可行的。

(2) 仅一衬支护条件下拱顶中心内侧、拱肩内侧和边墙中心内侧以及仅二衬厚度为0.5 m条件下边墙中心内侧拉应力值超过强度设计值，衬砌可能会发生拉裂破坏。

(3) 仅一衬支护条件和一衬与二衬联合支护条件下衬砌变形为协调变形，径向位移最大处为顶拱中心。