基于优化BP神经网络算法的隧道岩土体力学参数分析方法研究

龚 盛，杨 柱，张国鹏，罗 曦，陈兴周

(1. 西安科技大学 建筑与土木工程学院,西安 710054；2. 中国电建集团西北勘测设计研究院有限公司,西安 710065)

0 前 言

隧道开挖破坏了地层的天然应力状态，受赋存现场的地下水、隧道上覆荷载、施工方式等复杂工程条件的影响，引起应力重分布并随时程而变化[1]。而由于土体结构的复杂性以及土体材料的非均质、非线性、不连续的特性，使得土力学参数的确定一直是工程界的难题之一，为此，获取符合实际的围岩参数进行支护设计尤为重要[2-3]。土体力学参数可以通过室内试验和原位试验获得，然而，这些试验获得的参数都是试样的力学参数，实际工程中土层的性状复杂，试样的力学参数无法很好的反映土层的强度、变形特征[4]。基于现场监测的位移反分析方法是确定土体力学参数的有效方法之一，并且其在隧道的稳定性评价、施工设计以及变形预测中发挥着重要作用。

范新宇[5]等针对水库边坡变形受水位线升降影响的特点，采用神经网络预测了库水位变化和降雨对边坡变形的影响；张争[6]等利用Phase2联合 MATLAB神经网络工具箱进行围岩参数反演，进行隧洞围岩变形分析，计算结果与监测数据变化规律一致；柏俊磊[7]采用BP神经网络对水电站高边坡进行参数反演，通过有限元计算验证所得参数能较好地反应岩体开挖后的位移变化规律。Zheng Zhaoliang[8]等采用人工神经网络模型(ANN)和粒子群优化模型算法对边坡进行位移反分析，根据不同开挖阶段的监测位移数据获得岩体的弹性模量；Yong Zhao和Shi-Jin Feng[9]在考虑了位移损失和空间效应的基础上，使用粒子群优化算法优化极限学习机，提出了一种基于岩石位移参数反演的方法；原先凡[10]等基于有限差分软件建立模型，并利用BP神经网络模型对考虑开挖卸荷状态下的隧道围岩力学参数进行反分析；张志华[11]等基于神经网络计算分析了土体变形量与其对应的力学参数之间的非线性关系。

本文将CO-RDPSO算法优化神经网络运用到隧道工程反分析当中，根据监测位移反演土体力学参数，并且用文献算例进行了验证并反演参数，可为后续支护设计安排提供参考。

1 基于 CO-RDPSO 神经网络的参数反演方法

在隧道稳定性分析中，土体力学参数选取的合理性决定着计算的正确性，因此有必要进行土体力学参数反演，获得与工程较为符合的土体力学参数尤为重要。土体力学参数的辨识一般有正分析和反分析两种。正分析即是通过室内试验、原位试验或力学计算等方法进行正向确定参数；反分析则是通过现场监测位移等结果数据来逆向确定参数的方法。受地质体构造复杂性等的影响，通过正向分析得到的参数与工程实际相差较大。本文采用位移反分析的方法并基于BP神经网络算法来获取隧道土体力学参数。

1.1 BP神经网络

BP神经网络是一种前向传播的神经网络，由输入层、隐含层、输出层构成输入数据与输出数据间的非线性映射，它的信息是正向传递的，误差则是反向传播的，其基本思想是将预测值与期望间的误差由输出层反向传播，用以调整各个连接神经元之间的权值和阈值，通过多次迭代误差找到合适权值和阈值，使误差逐渐减小，网络实际输出值不断逼近期望输出，神经网络信息传递方式如图1所示。常规的BP神经网络采用梯度下降法对误差进行传播, 但由于初始权值和阈值是随机设定的，使得BP神经网络常出现、易陷入局部最优、网络学习率不稳定、收敛速度慢等缺陷。

图1 BP神经网络结构

1.2 交叉算子的随机漂移粒子群算法CO-RDPSO

粒子群优化算法(Particle Swarm optimization,PSO)是Poli R和Kennedy J[12]提出的进化算法的一个重要分支，是一种通过全局粒子最优位置和粒子个体最优位置调整下次迭代位置的寻优计算方法。在寻找函数最小值方面具有很强的优化性能，并且收敛速度快。

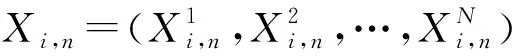
(1)

(2)

公式(1)～(2)中：W是惯性权重；c1和c2是学习因子，用于调整算法的收敛速度；r1，r2为在[0，1]范围内正态分布的随机数。

(3)

公式(3)表明整个种群的收敛会使每个粒子在各自的Pi,n和Gn组成的超矩形附近进行搜索，反映了标准PSO 算法中粒子偏局部的搜索行为，使得标准 PSO 算法在迭代后期易于陷入局部收敛。

(4)

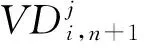
(5)

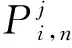
(6)

(7)

综上，RDPSO算法的速度更新公式可写为：

(8)

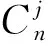
Holland 受自然界生物进化提出了遗传算法，该算法自20世纪70年代提出以来在解决优化问题上得到了广泛的使用[15]，其中交叉算子是遗传算法优化的主要工具，将交叉算子运用到粒子群算法上也有着优秀的表现。交叉学习可以利用已有的优秀粒子构造新的粒子，不仅可以提高粒子的种群多样性，避免粒子过早收敛，同时使得粒子的搜索范围更大，更有机会跳出局部收敛。

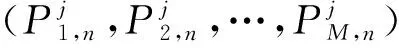
(9)

(10)

R=(t/nmaxiter)×M

(11)

公式(11)中:t为迭代次数；nmaxiter为最大迭代次数；M为粒子总数。

(12)

(13)

最后应用随机漂移粒子群算法进行速度和位置的更新，如公式(8)和公式(2)所示。

1.3 CO-RDPSO优化神经网络反演流程

基于CO-RDPSO 算法的隧道力学参数反演分析流程如下：首先依据地质及施工资料建立隧道数值仿真模型，在反演参数取值范围内进行均匀采样，带入数值模型计算生成训练样本。采用CO-RDPSO 算法对 BP神经网络的初始权值和阈值进行优化，使神经网络能够更好地反映隧道变形与围岩力学参数之间的非线性映射关系。将实测位移带入训练好的神经网络，通过不断迭代优化寻找最贴近实际监测数据的材料参数，最后利用数值模型和计算反演参数下隧道的位移，通过计算位移与实测位移的对比评价反演效果。

2 工程算例

2.1 数值模型

采用文献[16]中的案例验证CO-RDPSO算法优化BP神经网络的效果。某地铁隧道采用盾构施工，隧道外径 6.0 m，衬砌厚 0.3 m，建模时采用实体单元模拟衬砌，土体密度1 800 kg/m3，其他参数详见表 1。地表覆盖 3～5 m厚杂填土，主要由黏性土、石灰岩碎石、建筑垃圾以及生活垃圾等组成，下层主要是中风化白云质灰岩，岩体节理裂隙较发育。

表1 土体参数参考值

依据文献资料建立的数值模型如图2所示，模型的尺寸为50 m×40 m×30 m(长×宽×高)，模型的四周和底面设置法向约束，模型顶面采用自由边界，由于隧道中心点到模型顶面的距离小于隧道中心点到实际地面的距离，在模型顶面施加1.4 MPa的法向力，用于模拟土层和地面荷载。隧道采用全断面开挖法施工，开挖进尺为2 m，在隧道拱顶和拱腰处设置两个监测点，监测该处的位移值作为数据集输入样本，将数据集分为训练集和测试集对神经网络进行训练，并测试神经网络的预测效果。

图2 数值计算模型

模型采用的力学参数如表1所示。结合表1中参数的变化区间，丁德馨[17]等采用数理统计分析方法确定了弹塑性位移反分析的可反演参数，其中对变形影响最大的参数主要是弹性模量和泊松比，因此本文主要对弹模和泊松比进行反演，将弹性模量、泊松比均匀分为5个水平，进行正交实验，得到了25个训练样本集，将数值模拟得到的位移值作为数据集输入值，土体力学参数作为输出值，得到初始数据集对神经网络进行训练与验证，学习样本如表2所示。

表2 神经网络学习样本

2.2 构建样本集训练神经网络

利用CO-RDPSO算法优化 BP 神经网络权值和阈值，研究表明隐含层数量对BP神经网络的准确性影响不大[18]，并且过多的隐含层可能会导致神经网络出现过拟合的现象，因此本文只选取了一层隐含层，隐含层神经元个数为12个，以均方误差MSE作为目标函数，利用粒子群算法进行多次寻优计算，单次计算时最大迭代次数为200次，以多次训练中目标函数最小处粒子的位置作为神经网络的初始权值和阈值，即完成了神经网络的训练。

将隧道开挖2 m处断面的实测值代入训练好的神经网络，其训练迭代过程误差曲线如图3所示，图3中的适应度即为误差均方MSE，随着迭代的进行误差逐渐减小，当误差趋于最小时建立最终的BP神经网络。利用神经网络计算得到土体杨氏模量为0.358 2 GPa、泊松比μ为0.271 4，因为选取的神经网络训练样本不一样，本文所得土体力学参数与文献计算结果有一定误差，但两文中参数值非常接近。

图3 BP神经网络训练误差曲线

2.3 结果分析

将E、μ带入数值模型获取模拟位移值，其位移对比如图4所示，拱顶与拱腰反演参数模拟位移与监测位移误差分别为0.2% 和 0.75%，分析误差产生的原因主要有：① 粒子群粒子个数设置为100个，相较于神经网络权值阈值个数较少；② 本文采用的为单目标粒子群优化算法，目标函数仅有一个，可将平均绝对误差、均方根误差作为目标函数，得到不同目标函数下的神经网络。

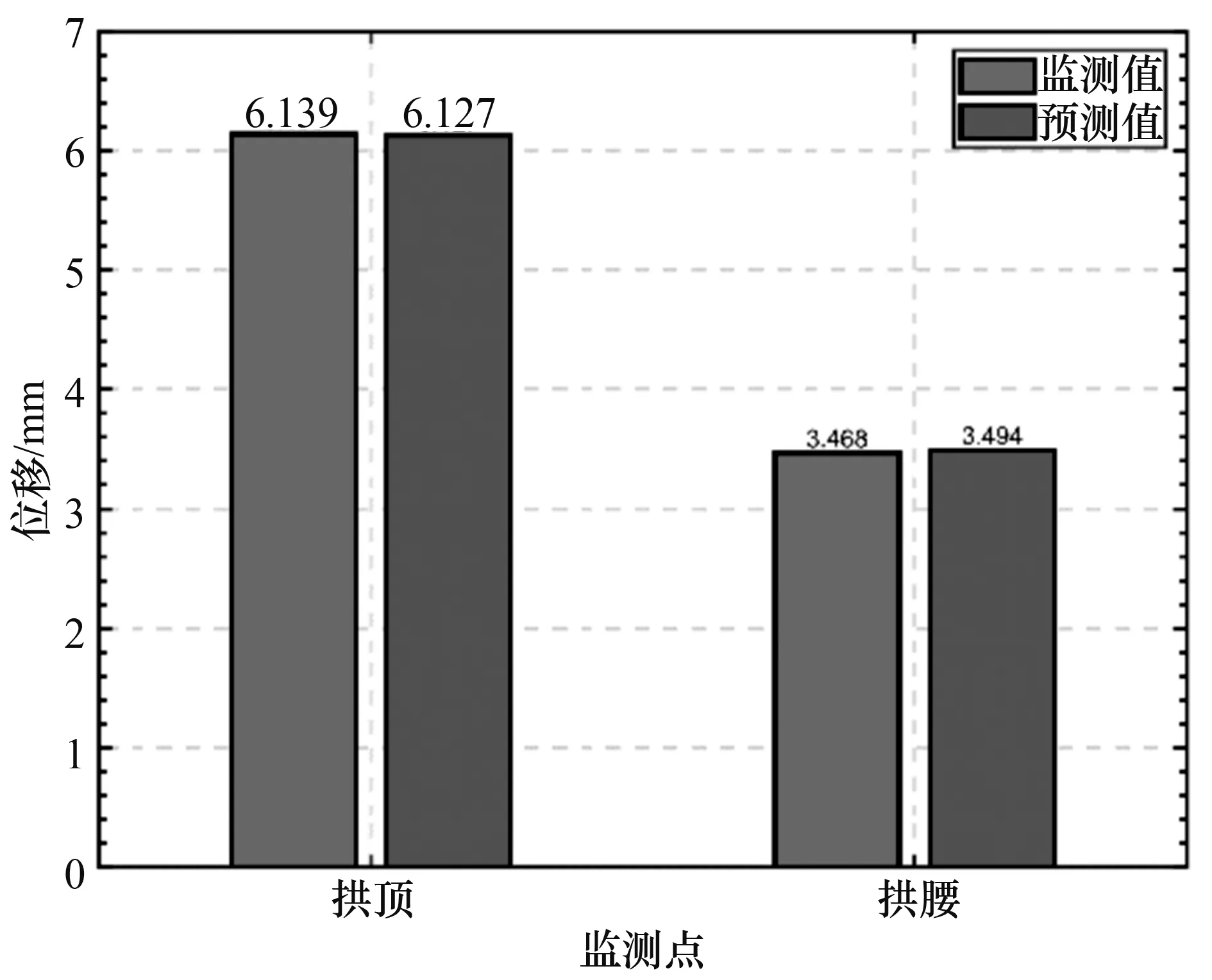
图4 监测点计算位移与预测值对比

3 结 论

(1) 基于神经网络,对利用正交设计试验并结合数值模型的样本集进行训练,得到了训练收敛的神经网络,可以方便地反演计算围岩力学参数。

(2) 采用CO-RDPSO算法，不仅能提高其全局搜索能力，还能够加快神经网络的收敛速度，改善神经网络易于陷入局部最优解的问题，又利用了神经网络非线性映射特点，从而能够得到反演参数的最优解。