预应力UHPC-NC组合梁抗弯承载力计算方法

朱劲松，秦亚婷，史腾

(1.天津大学 建筑工程学院，天津，300072；2.天津大学 滨海土木工程与安全教育部重点实验室，天津，300072)

超高性能混凝土(UHPC)是一种新型高性能纤维增强水泥基复合材料。与传统的普通混凝土(NC)相比，UHPC具有优异的力学性能，如超高的抗压强度和抗拉强度、低渗透性、高耐久性等[1-3]。部分或全部采用UHPC材料可以改善桥梁结构的性能[4]，将预制UHPC 梁单元与NC 桥面板通过抗剪连接件连接组成的UHPC-NC组合梁桥可以充分发挥UHPC的抗拉性能及NC的抗压性能，同时提高结构的承载能力和耐久性，优化桥梁上部结构尺寸，并减轻结构自重。该结构形式在充分利用UHPC 优良性能的同时降低了造价，成为适用于中、小跨径桥梁的新型结构形式。

VOO 等[5-6]介绍了由UHPC 预制梁和现浇NC桥面板构成的组合公路桥的制作工艺、施工顺序以及设计方法；李昭等[7]提出了一种新型装配式双工字型UHPC-NC组合梁结构，并进行了缩尺模型试验和有限元分析，研究了配筋率、UHPC 抗拉、压强度及桥面板强度等级对组合梁抗弯性能的影响；季文玉等[8]通过试验方法研究了活性粉末混凝土(RPC)应用于梁结构叠合梁的抗弯延性性能，研究结果表明RPC 材料优异的力学性能以及钢纤维的存在提高了叠合梁峰值荷载后的变形能力；LI等[9]对UHPC-NC 叠合梁的抗弯性能进行了试验和理论研究，发现将UHPC应用于预应力混凝土梁的受拉区，可以显著提高构件的刚度和延性。现有研究已表明UHPC组合结构具有良好的力学性能及工程应用价值，然而，目前国内仍缺乏有效指导UHPC组合结构设计的规范。

为有效预测预应力UHPC-NC组合梁的抗弯承载力，指导UHPC-NC组合梁桥的设计，本文作者提出预应力UHPC-NC组合梁的抗弯承载力计算方法；建立预应力UHPC-NC组合梁的抗弯承载力理论计算公式，并将公式计算值与有限元模拟值进行对比，以验证抗弯承载力计算公式的适用性。

1 预应力UHPC-NC组合梁概况

预应力超高性能混凝土-普通混凝土(UHPCNC)组合梁由预制工字型UHPC梁单元和覆盖于其上的NC翼缘板通过预埋在UHPC梁单元中的抗剪钢筋连接组成，以下简称为预应力UHPC-NC组合梁。预应力UHPC-NC组合梁可以减少钢筋用量和构件截面尺寸，降低结构自重，在大跨度和重荷载结构应用中有明显的优势。预应力UHPC-NC组合梁结构示意如图1所示。预制UHPC梁单元顶缘预留钢筋连接件，竖向抗剪钢筋伸出预制UHPC梁顶缘兼作钢筋连接件，实现与现浇NC翼缘板间的剪力连接。

图1 预应力UHPC-NC组合梁示意图Fig.1 Schematic diagram of prestressed UHPC-NC composite beam

2 预应力UHPC-NC 组合梁有限元分析

2.1 材料本构模型

预应力UHPC-NC 组合梁的材料模型包括UHPC、普通混凝土、预应力筋、普通钢筋模型。2.1.1 UHPC本构模型

UHPC 的受压应力-应变关系采用文献[10]提出的UHPC 受压本构模型，其应力-应变关系曲线如图2(a)所示，表达式如下：

式中：σ为UHPC 受压应力；ε为UHPC 受压应变；fc为UHPC 轴心抗压强度；ε0为UHPC 的峰值压应变；UHPC应变比ξ=ε/ε0；UHPC受压峰值应变n=E0/Esl；应力峰值点的切割模量Esl=fc/ε0；E0为初始弹性模量。

UHPC的受拉应力-应变关系采用文献[11]提出的UHPC受拉本构模型，其应力σ-应变ε关系曲线如图2(b)所示，其中fct为UHPC应变硬化阶段平均应力；εca为线性偏离初裂应变；εpc为极限应变。

图2 UHPC应力-应变关系曲线Fig.2 Stress-strain relationship curves of UHPC in compression and tension

2.1.2 NC本构模型

NC的单轴受压应力-应变关系表达式如下：

式中：fc，r为轴心受压强度；εc，r为与fc，r对应的混凝土峰值压应变；Ec为混凝土弹性模量；αc为混凝土单轴受压应力-应变曲线下降段的参数，αc=0.157fc0.785-0.905；NC单轴受压应变比x1=ε/εc，r。

NC的单轴受拉应力-应变关系表达式如下：

式中：ft，r为轴心受拉强度；εt，r为与ft，r对应的混凝土峰值拉应变；αt为混凝土单轴受拉应力-应变曲线下降段的参数，αt=0.312f2t，r；NC 单轴受拉应变比x2=ε/εt，r。

2.1.3 普通钢筋本构模型

钢筋本构采用理想弹塑性模型，其应力-应变关系表达式如下：

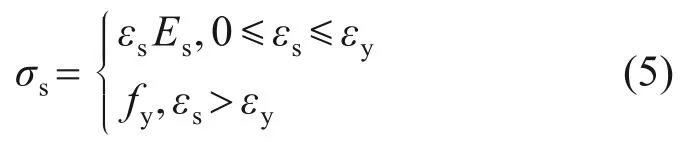
式中：Es为钢筋弹性模量；fy为钢筋的屈服强度；εy为钢筋达到屈服强度时对应的峰值拉应变。

2.1.4 预应力筋本构模型

预应力钢绞线本构关系采用双斜线弹塑性模型，其应变-应力关系表达式如下：

式中：fy为预应力钢绞线屈服强度；fu为预应力钢绞线极限强度；εu为极限拉应变；Ep为钢绞线弹性模量。

本文在ABAQUS 中采用塑性损伤模型(damaged plasticity)模拟UHPC 和NC 的材料性能，混凝土塑性损伤模型中除定义材料本构关系外，还需确定与塑性准则等相关的参数，根据ABAQUS手册中的推荐值，定义膨胀角为30°，偏心系数为0.1，双轴抗压强度与单轴抗压强度之比为1.16，不变应力比为0.666 7，黏性系数为0.001。

2.2 UHPC-NC界面模拟方法

UHPC 与NC 均为水泥基材料，材料性质相近，UHPC-NC 界面黏结性能良好[12-13]。然而，对于UHPC-NC界面行为的模拟，现有研究中还没有统一的方法。ABAQUS 中提供了多种模拟界面行为的选项，其中主要包含以下3种：1) 使用完全黏结(tie)对界面行为进行模拟，这种模拟方式认为2个接触面之间不会发生相对滑移[14]；2) 采用默认的法向硬接触和切向摩擦因数相结合的方式对界面行为进行模拟，该方法计算时忽略了界面间的黏聚力影响，仅考虑了界面间摩擦因数的影响，会低估界面间的黏结强度[15]；3) 采用接触-分离模型(黏聚力模型)模拟界面的接触行为，该模型同时考虑了界面间的黏聚力和摩擦因数的影响，是一种较为理想的接触设置方式[16]。

本文分别采用以上3 种方法对文献[7]中的UHPC-NC 组合梁缩尺模型进行有限元建模，其中接触-分离模型采用最常用的双线性本构模型。3种UHPC-NC界面模拟方式下得到的有限元模拟结果如图3 所示。由图3 可见：使用完全黏结(tie)以及采用接触-分离模型(黏聚力模型)对界面行为进行模拟得到的有限元计算结果均能较好地与试验结果吻合，但采用接触-分离模型模拟时，计算成本较高。经综合考虑，本文采用完全黏结(tie)模型对UHPC-NC界面行为进行模拟。

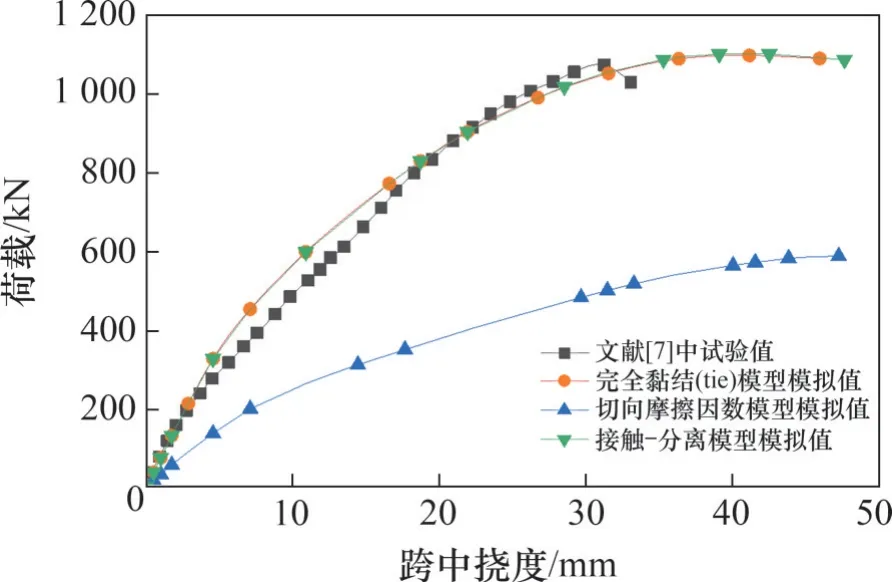
图3 组合梁界面模拟方法对比Fig.3 Comparison of interface simulation methods for composite beams

2.3 试验验证

李昭等[7]根据实际工程尺寸设计了一根缩尺比例为1∶2 的UHPC-NC 组合梁模型，并进行了抗弯试验，以研究UHPC-NC组合梁的抗弯性能。试验梁总长7.5 m，桥面板宽度为580 mm，试验梁上部采用现浇C50普通混凝土，现浇桥面板配筋为两层直径为8 mm 的纵横向钢筋，箍筋采用直径为10 mm的单肢箍，东西两侧间距分别为100 mm和50 mm，下翼缘配筋为直径为20 mm 的受拉主筋，钢筋型号均为HRB400。

李立峰等[17]设计了一根大比例预应力UHPC-T形梁，并进行了抗弯试验，以研究预应力UHPC梁的抗弯性能。试验梁总长10 m，计算跨径9.8 m，试验梁采用后张预应力构件，上下翼缘分别布置5根和8根直径均为12 mm的纵向钢筋，箍筋采用直径为12 mm 的单肢箍，间距为100 mm，钢筋型号均为HRB335，下翼缘配筋为2束直线1860级预应力钢绞线。

通过有限元分析软件ABAQUS 建立文献[7]中UHPC-NC 组合梁和文献[17]中预应力UHPC-T 形梁的数值分析模型，材料力学性能分别见表1和表2，并进行单元选取、相互作用及边界条件设定及网格划分。采用完整的三维模型进行建模，NC和UHPC 采用八节点实体单元(C3D8R)建模。对于试件中的纵向钢筋及预应力筋，采用两节点桁架单元(T3D2)建模，钢筋保护层厚度为25 mm，网格尺寸为50 mm。边界使用简支条件建模，采用位移控制加载。混凝土与钢筋骨架采用嵌入(embedded)连接方式，混凝土与垫块之间采用完全黏结(tie)连接，UHPC 与普通混凝土之间采用完全黏结(tie)连接。

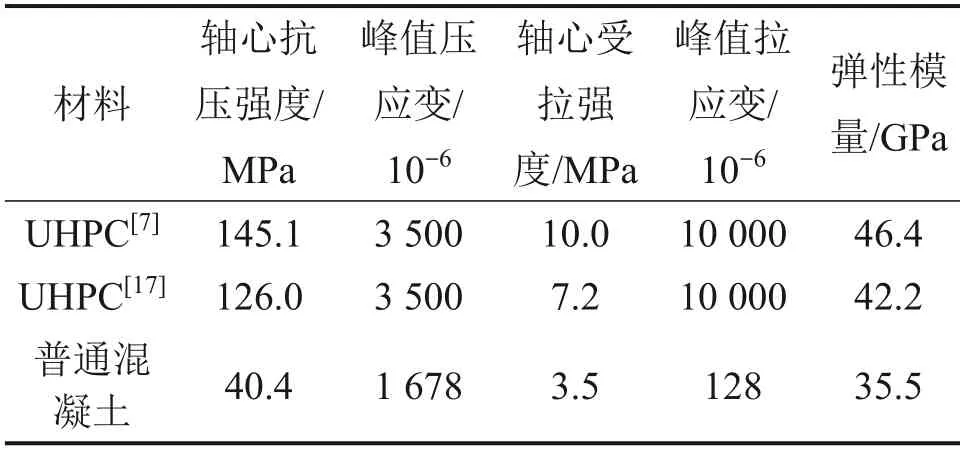
表1 UHPC及普通混凝土基本力学性能Table 1 Basic mechanical properties of UHPC and concrete

表2 钢筋基本力学性能Table 2 Basic mechanical properties of reinforcement

将ABAQUS 有限元模拟结果与抗弯试验结果进行对比，从而验证有限元数值模拟方法的准确性。UHPC-NC 组合梁及预应力UHPC-T 形梁有限元计算得到的荷载-跨中挠度曲线与试验曲线的比较如图4所示。由图4可知，本文有限元模拟结果与抗弯试验结果吻合良好，验证了本文所建立的UHPC-NC 组合梁和预应力UHPC-T 形梁有限元模型的准确性和可靠性。

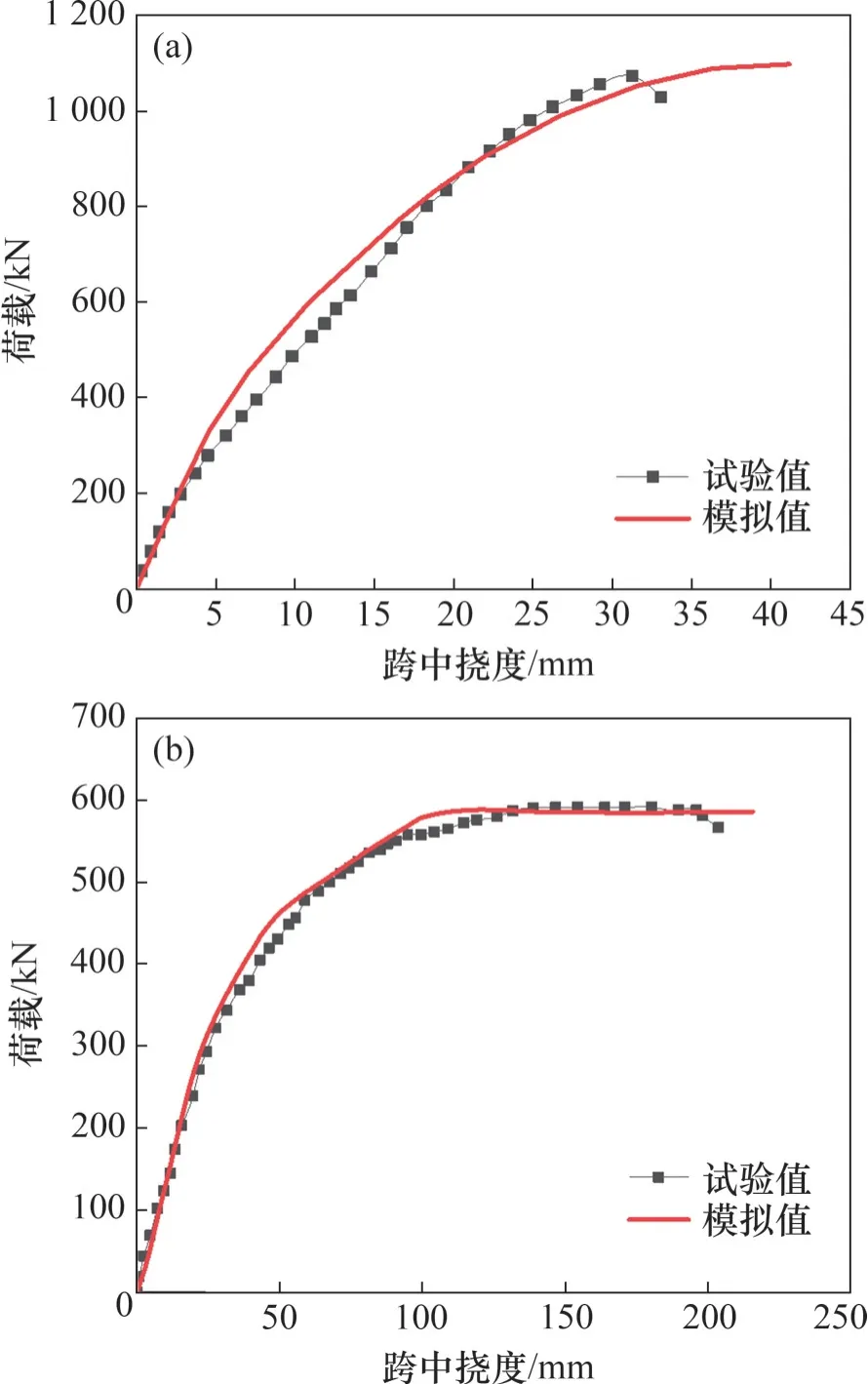
图4 荷载-跨中挠度有限元计算曲线与试验曲线比较[7,17]Fig.4 Comparison of finite element calculation curves and experimental curves of load-deflection[7,17]

3 预应力UHPC-NC 组合梁抗弯性能分析

3.1 预应力UHPC-NC组合梁数值模型

本文预应力UHPC-NC组合梁总长为30 m，梁肋下部布置5 根直径为25 mm 的受拉主筋。混凝土桥面板中横向钢筋铺设间距为500 mm，纵向钢筋间距为100 mm，钢筋直径均为16 mm。箍筋为直径为16 mm 的单肢箍筋，箍筋间距为100 mm。钢筋规格均为HRB400。采用2 束ϕs15.2-6(每束包含6 根直径为15.2 mm 的钢绞线)的1860 级钢绞线作为预应力筋，预应力筋张拉控制应力为1 395 MPa。预应力UHPC-NC 组合梁尺寸构造如图5所示。

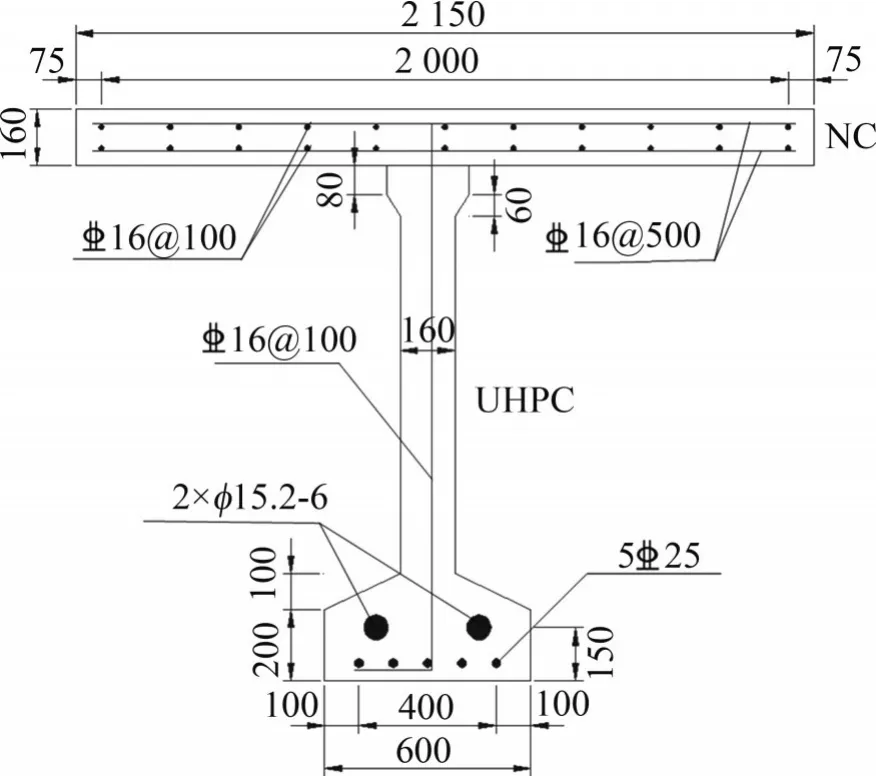
图5 预应力UHPC-NC组合梁构造图Fig.5 Structure diagram of prestressed UHPC-NC composite beam

对预应力UHPC-NC 组合梁进行受弯模拟分析，其中UHPC和NC材料参数采用文献[7]中的实测值。预应力UHPC-NC 组合梁计算模型如图6所示。

图6 预应力UHPC-NC组合梁有限元模型Fig.6 FE model of prestressed UHPC-NC composite beam

3.2 破坏模式

对于预应力UHPC结构，由于UHPC在开裂之后仍然具有一定的抗拉强度，预应力筋不会立即屈服，结构不会发生脆性破坏[17]。根据NC压碎和预应力筋屈服及拉断发生的先后顺序不同，预应力UHPC-NC组合梁破坏模式可分为超筋梁脆性破坏和适筋梁破坏，当结构配筋率过大时，会导致受压区NC压碎时预应力筋未屈服，发生超筋梁破坏。适筋梁塑性破坏又可分为受压区混凝土压碎破坏和预应力筋拉断破坏。当配筋适当时，预应力筋屈服后，受压区混凝土压碎先于预应力筋拉断发生，受压区混凝土发生压碎破坏；反之，则发生预应力筋拉断破坏。

对于预应力UHPC-NC组合梁，跨中截面受压混凝土应变及受拉预应力筋应变与跨中挠度的关系如图7所示，预应力筋应力随跨中挠度变化如图8 所示。由图7 与图8 可见：当受压区混凝土达到极限压应变0.003 时，组合梁预应力筋应力fps为1 813 MPa，组合梁预应力筋已经屈服，但预应力筋尚未达到极限拉应变εpu=0.035，说明组合梁预应力筋屈服后，受压区混凝土压碎先于预应力筋拉断发生，表现为受压区混凝土被压碎破坏。

图7 应变与挠度关系曲线Fig.7 Relationship curve between strain and deflection

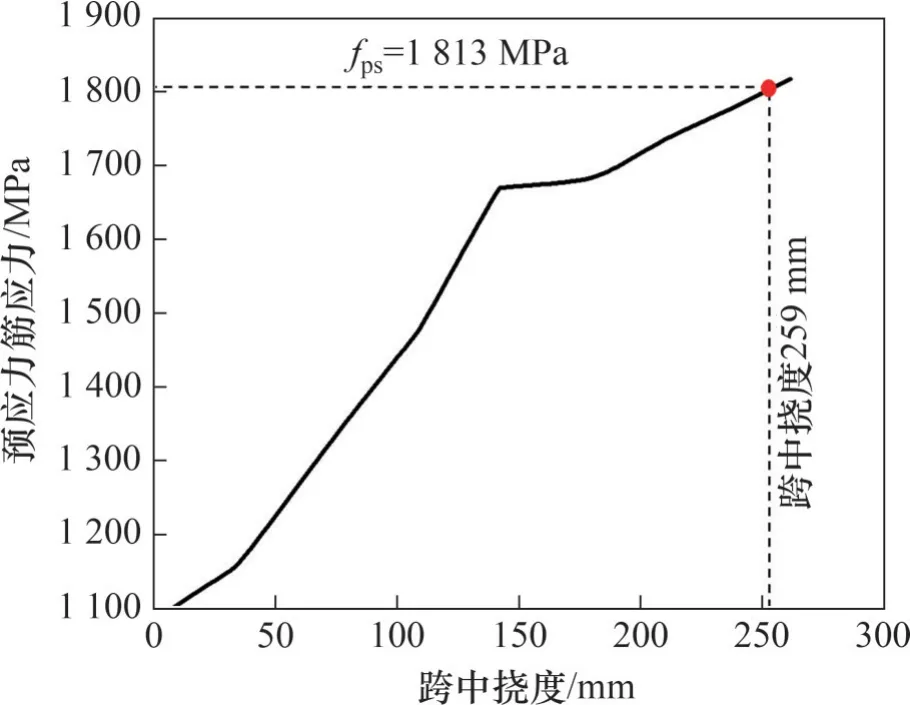
图8 预应力筋应力变化曲线Fig.8 Stress variation curve of prestressed tendon

3.3 参数分析

本文系统地分析了预应力筋配筋率、普通钢筋直径、普通钢筋强度等级以及高跨比等参数对预应力UHPC-NC组合梁抗弯承载能力的影响。预应力UHPC-NC组合梁参数以及本文抗弯承载力公式计算结果与有限元计算结果对比见表3。参数变化对预应力UHPC-NC 组合梁抗弯性能的影响见图9。

由表3和图9可知，提高预应力筋配筋率、普通钢筋直径和高跨比均可显著提高预应力UHPCNC组合梁极限抗弯承载力，普通钢筋强度等级对组合梁极限抗弯承载力影响不明显；组合梁开裂前的抗弯性能受高跨比影响较大，增大高跨比可以有效提高组合梁弹性阶段抗弯刚度；预应力筋配筋率、普通钢筋直径和普通钢筋强度等级对组合梁开裂前的受弯性能没有显著影响。

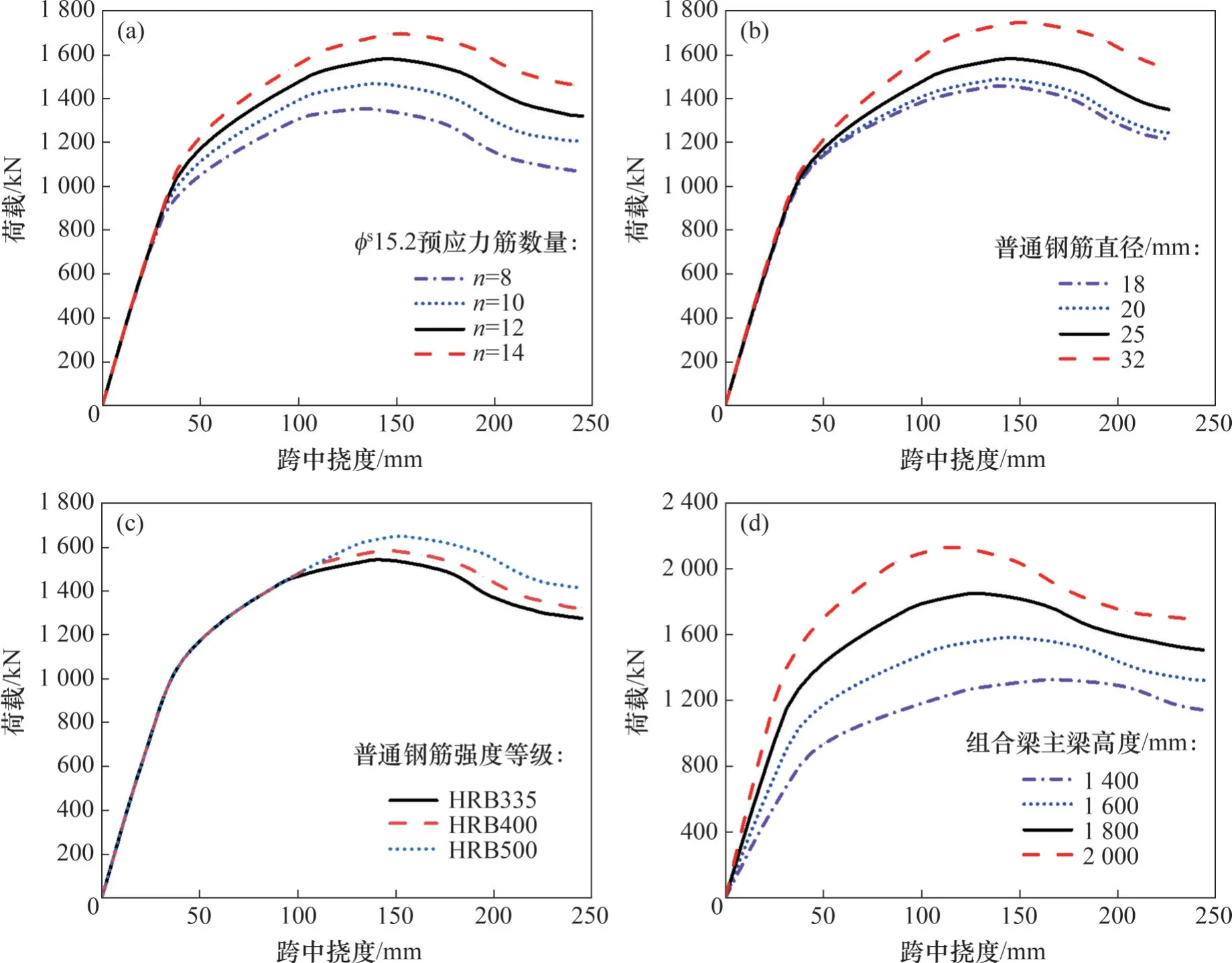
图9 各参数变化对预应力UHPC-NC组合梁抗弯性能的影响Fig.9 Influences of various parameters on the flexural performance of prestressed UHPC-NC composite beams

表3 组合梁参数信息以及抗弯承载力公式计算结果与有限元计算结果对比Table 3 Composite beam parameter information and comparison of calculation results with finite element calculation results of flexual capacity

4 受弯承载力分析

4.1 基本假定

与一般钢筋混凝土梁类似，计算预应力UHPC-NC 组合梁抗弯承载力时，采用以下基本假设：1) NC翼缘板和预制UHPC梁单元之间存在可靠连接，相对滑移很小，可以忽略不计；2) 组合

梁截面上UHPC、NC、预应力筋和钢筋应变均符合平截面假定；3) 当组合梁达到极限状态时，受压区混凝土部分已进入塑性状态，将截面受压区NC 和UHPC 应力图形简化为矩形，压应力分别取为NC 和UHPC 的轴心抗压强度；4) 考虑受拉区UHPC对抗弯承载力的贡献，将受拉区UHPC应力图形简化为矩形，其拉应力基于安全考虑取为λ倍抗拉强度(λ≤1)，其中λ为受拉区UHPC等效矩形应力系数[18]，受拉区等效矩形拉应力为λftd，其中，ftd为UHPC抗拉强度。

将组合梁截面进行简化处理，将上翼缘承托部分和下翼缘马蹄处按等面积原则简化为矩形截面。基于上述假定，承载力极限状态时UHPC-NC组合截面应力应变分布如图10所示。

图10 中，M为组合梁抗弯承载力；hf1为普通混凝土受压翼缘高度；bf1为普通混凝土受压翼缘宽度；bf2为受拉UHPC 翼缘宽度；hf2为受拉UHPC 翼缘高度；b为UHPC-NC 组合截面腹板宽度；h为UHPC-NC 组合截面高度；fsd为纵向普通钢筋的抗拉强度设计值；As为受拉区纵向普通钢筋面积；f′sd为纵向普通钢筋的抗压强度设计值；A′s为受压区纵向普通钢筋面积；ftd为UHPC轴心抗拉强度；fcd为UHPC 轴心抗压强度设计值；fcd1为普通混凝土轴心抗压强度设计值；fpd为纵向预应力钢筋的抗拉强度设计值；Ap为受拉区纵向预应力钢筋的截面面积。β为受弯构件受压区高度x与实际受压区高度xc的比值，对于C50 混凝土，取0.8[19]；xt为组合梁受拉区等效高度；对于UHPC结构，参考“公路桥涵超高性能混凝土应用规范(征求意见稿)”取0.82；对于组合截面本文统一取为0.82。

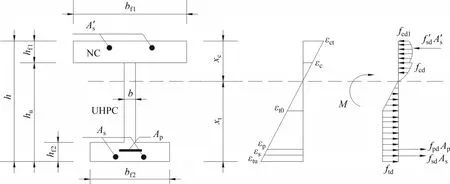
图10 组合梁截面应力-应变分布图Fig.10 Stress-strain distribution of cross section of composite beams

4.2 抗弯承载力计算方法

在计算截面的极限弯矩时，应先判断所属的截面类型，根据受压区高度不同，受拉区和受压区的合力计算以及极限抗弯承载力的计算分为以下2 种情况：当受压区高度在NC 翼缘板内，截面为第一类截面；当受压区进入UHPC腹板区域，截面为第二类截面。

当满足式(7)时，受压区高度在NC 翼缘板内，抗弯承载力按第一类截面计算，截面简化应力分布如图11所示。

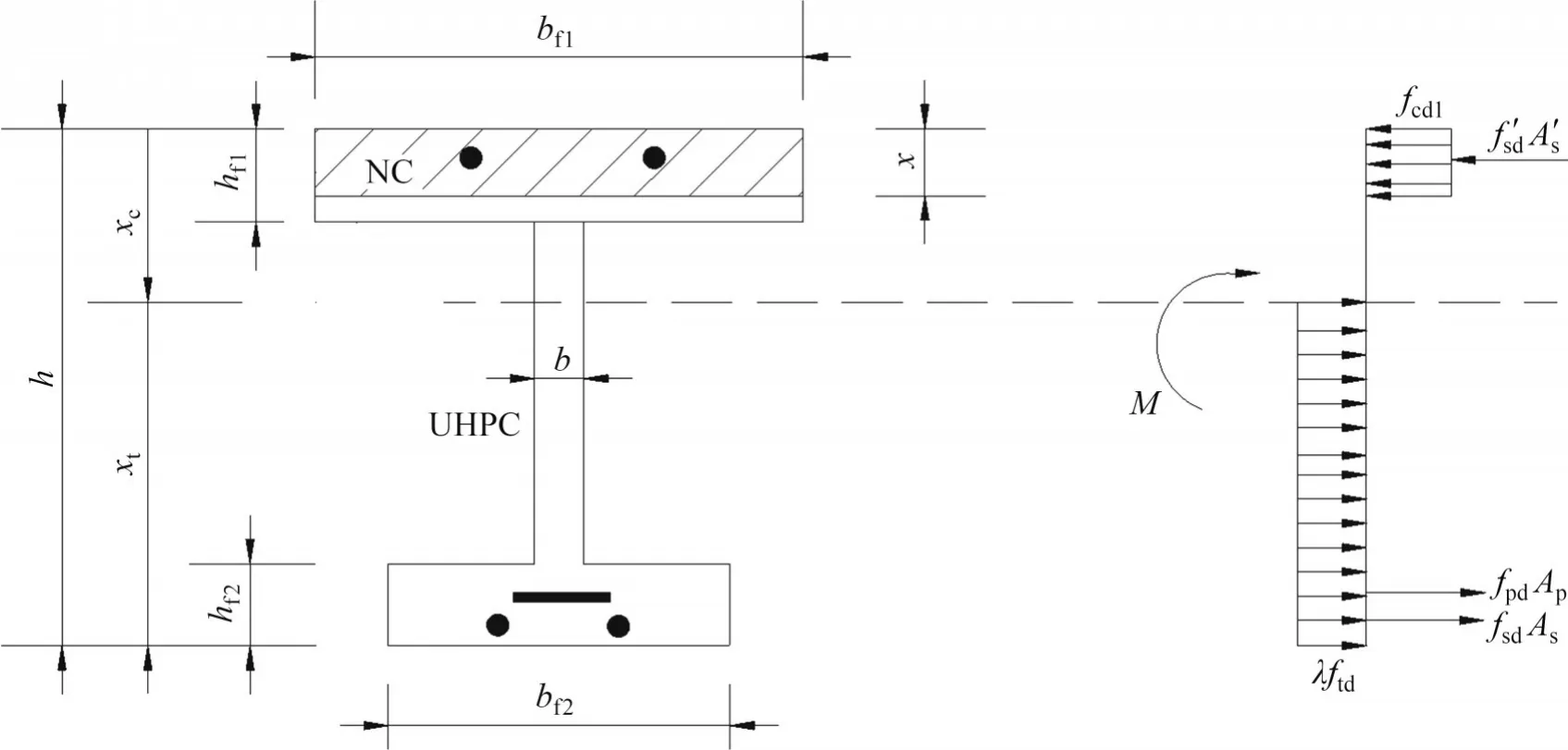
图11 组合梁第一类截面简化应力分布Fig.11 Simplified stress distribution of the first section of composite beams

由力的平衡条件可求出受压区高度x：

受拉区等效高度xt按下式计算：

对梁底受拉边缘取矩可得抗弯承载力Mu：

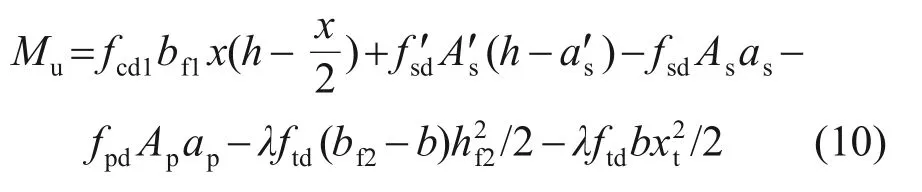
式中：as为受拉区普通钢筋合力点到受拉区边缘的距离；a′s为受压区普通钢筋合力点到受压区边缘的距离；ap为受拉区预应力筋合力点到受拉区边缘的距离。

当不满足式(7)时，受压区高度在UHPC 腹板内，抗弯承载力按第二类截面计算，截面简化应力分布如图12所示。

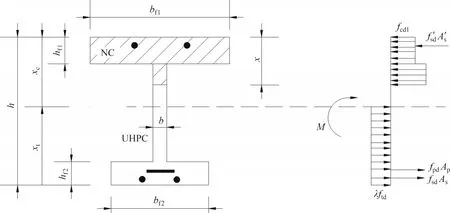
图12 组合梁第二类截面简化应力分布Fig.12 Simplified stress distribution of the second section of composite beams

由力的平衡条件可求出受压区高度x：

对梁底受拉边缘取矩可得抗弯承载力Mu：

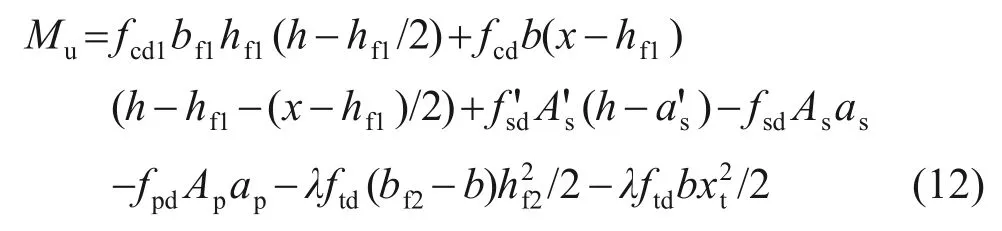
4.3 受拉区UHPC等效矩形应力系数取值比例

预应力UHPC-NC组合梁正截面抗弯承载力计算与普通钢筋混凝土梁不同，需要考虑受拉区UHPC抗拉强度对抗弯承载力的贡献。通过前面的分析可知，在计算组合梁抗弯承载力时，受拉区UHPC 的应力等效为矩形应力图，基于安全考虑，提出受拉区UHPC 等效矩形应力系数λ，当λ取值为0～1.0 时，预应力UHPC-NC 组合梁正截面抗弯承载力公式计算值与有限元模拟值比较如表4和图13所示。图13中，实线表示Mu公式计算值与有限元模拟值之比为1，虚线范围表示Mu公式计算值与有限元模拟值的相对误差小于20%[20]。

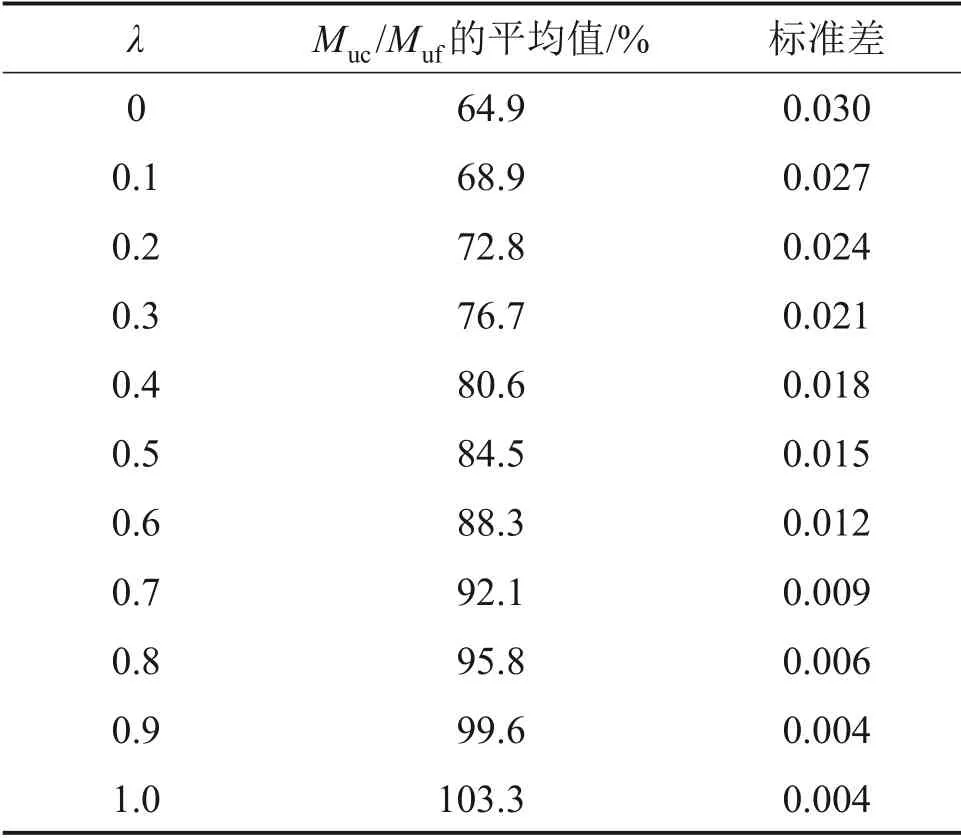
表4 不同λ下Mu公式计算结果与有限元计算结果对比Table 4 Comparison between calculation results of different UHPC tensile strength ratio and FE calculation results of Mu

图13 Mu公式计算值与有限元计算值对比Fig.13 Comparison between the calculated values of the formula and the calculated values of the FE of Mu

由表4和图13可知：当受拉区UHPC等效矩形应力系数为0即不考虑受拉区UHPC对抗弯承载力的贡献作用时，抗弯承载力公式计算值与有限元模拟值比值的均值为64.9%，标准差为0.03，抗弯承载力公式计算结果过于保守；当受拉区UHPC等效矩形应力系数为0.1～0.8 时，抗弯承载力公式计算值与有限元模拟值比值的平均值为68.9%～95.8%，标准差区间为0.006～0.027，抗弯承载力公式计算结果偏保守；当受拉区UHPC等效矩形应力系数为0.9时，抗弯承载力公式计算值与有限元模拟值比值的平均值为99.6%，标准差为0.004，抗弯承载力公式计算值与有限元模拟值吻合良好；当受拉区UHPC 等效矩形应力系数为1.0 时，抗弯承载力公式计算值与有限元模拟值比值的平均值为103.3%，标准差为0.004，抗弯承载力公式计算结果偏大，设计值安全性偏低。经综合考虑，设计时取受拉区UHPC等效矩形应力系数λ=0.9。

5 结论

1) 基于UHPC-NC界面模拟方法的研究，建立了预应力UHPC-NC组合梁的有限元分析模型，并通过试验验证了模拟方法的准确性和可靠性。提高预应力筋配筋率、普通钢筋直径和高跨比均可显著提高组合梁极限抗弯承载力，普通钢筋强度等级对组合梁极限抗弯承载力影响不明显。

2) 基于平截面假定、截面平衡条件以及UHPC、普通混凝土、预应力筋和钢筋的本构关系，提出了预应力UHPC-NC组合梁的抗弯承载力计算公式。通过有限元分析验证了计算公式的准确性和可靠性，抗弯承载力公式计算值与有限元模拟值比值的均值为99.6%，标准差为0.004，表明本文所推导出的抗弯承载力计算公式具有较高的精度。

3) 当预应力UHPC-NC组合梁达到极限承载力时，考虑受拉区UHPC对抗弯承载力的贡献，提出了受拉区UHPC 等效矩形应力系数λ，当λ取0.9时，抗弯承载力公式计算值与有限元模拟值吻合良好。