面向高温超导钉扎磁悬浮列车悬浮特性研究

张明亮 李明远 刘鹏飞 闫杨阳 刘丽茹 杨新梦

1.石家庄铁道大学机械工程学院，石家庄，050043 2.兰州交通大学光电技术与智能控制教育部重点实验室，兰州，730070

0 引言

磁悬浮列车的类型很多，常见的包括常导电磁悬浮列车[1]、低温超导电动磁悬浮列车[2]和高温超导钉扎磁悬浮列车[3-8]。常导电磁悬浮列车利用电磁吸力实现列车悬浮，需要精准的闭环控制系统；低温超导电动磁悬浮列车利用车载超导线圈(位于列车底部的液氦冷却装置中)与轨道侧壁的常导8字型线圈相互作用实现悬浮和导向，但是在低速未完全悬浮起来之前需要借助辅助车轮进行支撑；高温超导钉扎磁悬浮列车利用车载高温超导体(位于列车悬浮架底部的液氦冷却装置中)与永磁轨道的相互作用实现悬浮和导向。综合对比可知，具有我国完全自主知识产权的高温超导钉扎磁悬浮列车无需借助精确的主动控制也能实现静止时稳定悬浮，在直线电机的驱动下可实现无摩擦平稳运行，因此本文重点研究该类型磁悬浮列车。

为减小空气阻力、实现更高的速度，需要将真空管道技术与高温超导磁悬浮技术相结合，这类组合方式成为人们追求更高速度的新型交通系统[8-11]。我国目前已经成功建成全球首个真空管道超高速磁悬浮列车环形试验线系Super-Maglev，验证了真空管道高温超导磁悬浮的可行性[12-16]。在高温超导磁悬浮系统中，悬浮力和导向力是磁悬浮列车的主要性能指标，在工程化推广运行方面具有重要意义。目前的研究主要侧重于单块永磁体和永磁轨道等参数对高温超导体所受的悬浮力和导向力力学特性的影响，永磁轨道的优化分析大多集中在比较几种不同轨道下力学性能的优劣，具体量化的比较指标仍需深入研究，在优化过程中，简单计算悬浮力的方法较少。在动力学仿真研究方面，主要集中在高温超导磁悬浮系统的振动特性[17-21]。针对这种现状，本文对高温超导磁悬浮列车的悬浮力进行研究，为此提出了一种计算悬浮力简单有效的方法，为磁轨关系参数优化提供支撑。

目前永磁轨道的结构主要有单峰式结构、双峰式结构和三极对顶式结构等[22]，本文选用能提供较强磁场的双峰永磁轨道，测试了双峰永磁轨道和高温超导块组合的悬浮力，提出一种简单等效处理高温超导块组合的方法，通过改变场冷高度和悬浮间隙的参数研究悬浮力特性。

1 高温超导钉扎磁悬浮列车的工作原理

高温超导钉扎磁悬浮列车的悬浮是通过放置在车体底部的高温超导体与永磁轨道相互作用实现的，这种现象称为磁通钉扎效应，其原理如图1所示。永磁轨道为高温超导体提供磁源，将高温超导体固定于永磁体之上，两者之间留有一段距离，然后加液氮冷却。低温处理高温超导体之前外磁场可自由通过高温超导体，如图2所示，而低温处理高温超导体之后永磁体的磁场被高温超导体的钉扎点捕获固定，如图1所示，使两者呈现一种非接触稳定的连接，即能够使高温超导体稳定悬浮在永磁体之上。

图1 高温超导体磁通钉扎效应示意图

图2 外磁场在正常态高温超导体中的分布

高温超导体在生长过程中内部含有晶体缺陷和人为添加的杂质，使得高温超导体内部产生可以束缚磁场的钉扎点，即能够捕获磁轨的部分磁场，同时另一部分磁场又被阻止在高温超导体的外部无法渗入内部，此时高温超导体与磁轨在初始的场冷高度下保持非接触连接状态(无重力影响)。一旦释放高温超导体，受其重力的影响会向下轻微移动，由于外磁场具有梯度，高温超导体因外磁场的变化而感生出强电流，进而形成磁场，此时永磁轨道的磁场与其相反，两者相互作用产生斥力即可认定为悬浮力。当这种斥力与自身的重力相等时，高温超导体可以无任何支撑地悬浮于磁轨上方，同时高温超导体捕获磁通的能力使其具备导向力，因此可以使车载高温超导体的磁悬浮列车沿轨道纵向无摩擦地运行，本文重点对悬浮力进行研究。

为了后续表述方便，对文中的几个关键名词介绍如下：①场冷条件是指先将高温超导体放置在外磁场(由永磁体提供)中，再对高温超导体进行液氮低温冷却处理。②场冷高度是指在初始场冷条件下高温超导体上表面和永磁体下表面之间的轴向距离。③悬浮间隙是指永磁体轴向移动时高温超导体上表面和永磁体下表面之间的轴向距离。

2 悬浮力实验研究

2.1 实验装置

高温超导体和永磁轨道的悬浮力对稳定悬浮至关重要，本文对其进行实验研究。采用的悬浮力测试实验装置如图3所示，其结构原理示意图见图4。高温超导体固定在液氮低温容器中，双峰永磁轨道固定在移动架上。位移传感器位于永磁轨道移动架和基座之间，压力传感器位于低温容器和基座之间。电机带动永磁轨道上下往复移动，永磁轨道和高温超导体间的距离由位移传感器进行测量，悬浮力数据由压力传感器传给数据采集卡，测试系统对数据进行处理分析，将悬浮力数据导出。

图3 悬浮力测试装置

图4 悬浮力测试装置的结构示意图

目前已经研究出的三种不同结构的永磁轨道的磁场分布情况(箭头代表磁化方向)如图5所示，研究表明结构简单的单峰轨道更适用于实际中只用到永磁轨道中心位置磁场的高温超导悬浮列车，而结构复杂的双峰轨道具备较宽且较强的磁场，与单峰轨道相比能够为高温超导体提供更大的悬浮力和导向力，因此应根据实际需要选择合适结构的永磁轨道[25]。

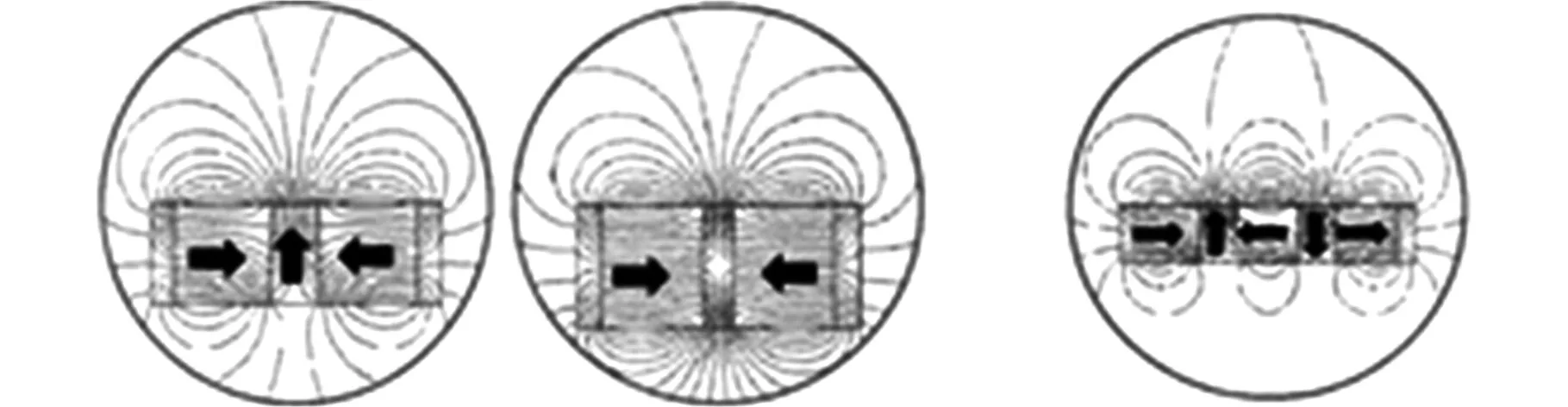
(a)单峰永磁轨道 (b)双峰永磁轨道

为了得到更大的悬浮力，本次实验采用双峰永磁轨道，轨道长度为800 mm，实物如图6所示；具体尺寸参数如图7所示，其中充磁方向为箭头方向，两边采用纯铁，主要磁场集中在中间两块纵向充磁永磁体上方。为了形成较大的超导平面，高温超导体利用多个高温超导块组合起来，简称高温超导块组合，具体采用10块高温超导块，单块尺寸为φ30 mm×14 mm，按5×2的方式排列，排列方式如图8所示。

图6 永磁轨道实物

图7 永磁轨道横截面图

图8 高温超导块组合图

2.2 实验结果分析

利用该装置测试双峰永磁轨道和高温超导块间的悬浮力数据，不同场冷高度下悬浮力和悬浮间隙的关系如图9所示。

(a)场冷高度为20 mm

悬浮力的测试实验过程主要分为3个阶段，以场冷高度20 mm的实验数据为例进行阐释，具体过程如下：

(1)初段上升过程。永磁轨道在20 mm场冷高度处逐渐上移至最高点60 mm，此段高温超导块所受的悬浮力为负值(吸引力)。可以观察到高温超导体在场冷高度处是不受力的(作用力等于0)；随着悬浮间隙的增大，吸引力先由0逐渐增大，约在32 mm时达到峰值-61.0 N，然后逐渐减小，到60 mm处悬浮力为-24.38 N。

(2)中段下降过程。永磁轨道由最高点60 mm处逐渐下移至最低点10 mm，高温超导块组合所受的悬浮力先表现为负值(吸引力)后表现为正值(排斥力)。随着悬浮间隙的减小，吸引力增大，约在39 mm处达到峰值-38.29 N，显然中段吸引力要小于初段吸引力，当永磁轨道移至24 mm时吸引力变为0，继续向下移动，悬浮力由吸引力转变为排斥力，随着悬浮间隙的减小和排斥力的迅速增大，在最低点10 mm处排斥力为200.98 N。

(3)后段上升过程。永磁轨道由最低点10 mm处逐渐上升移动至最高点60 mm，高温超导块组合所受的悬浮力先表现为正值(排斥力)后表现为负值(吸引力)，随着悬浮间隙逐渐增大，排斥力迅速减小，在18 mm处变为0，此时永磁轨道继续向上移动，排斥力转变为吸引力，在30 mm处达到峰值-62.32 N，最后吸引力逐渐减小，到60 mm处悬浮力为-25.11 N。

由图9可以观察到3个阶段在相同高度处的悬浮力不同，高温超导块组合初段悬浮力小于中段悬浮力，后段悬浮力小于中段悬浮力，初段悬浮力介于两者之间。产生这种现象的原因是高温超导体的磁滞作用，高温超导体捕获的磁场以磁通量子的形式被束缚在内部的针扎中心，捕获的磁场发生蠕动和强迫运动时不可避免地带来能量的损耗，使捕获磁场发生改变，从而造成悬浮力发生变化。因为初段悬浮力受磁滞影响较小，所以本文选取此段作为理论仿真研究的对象。

3 悬浮力理论研究

3.1 等效处理方法的提出

根据冻结镜像模型，可将高温超导块组合与永磁轨道之间的作用力分成斥力和引力两部分[23-24]。斥力通过设置高温超导体的低磁导率来实现，该过程模拟高温超导体的抗磁特性，相当于移动镜像；引力通过将高温超导体等效成具有磁化电流的磁体来实现，该过程模拟高温超导体的捕获磁场特性，相当于冻结镜像。利用该方法可以将高温超导块组合简化处理，由此可以计算高温超导块组合和永磁轨道间的悬浮力。具体处理的步骤如下：①将高温超导块组合的相对磁导率设置为0.001；②将超导体材料属性中的材料设置成钕铁硼，其中磁化电流可根据超导体与永磁轨道在场冷高度处的作用力为0来确定，即根据作用力为0并通过迭代计算流程得到高温超导体在场冷高度下的捕获磁场。

3.2 仿真三维模型的建立

为了利用等效处理方法，考虑到双峰永磁轨道磁场比较复杂，需要利用有限元软件对其进行建模。本文在Maxwell软件中搭建了双峰永磁轨道三维模型，其中永磁体材料设定为钕铁硼NdFe35，按给定的方式(图7)充磁，密度为7.4 g/cm3，相对磁导率为1.010，矫顽力Hc=942 kA/m，其磁场分布如图10所示。

(a)俯视图

为了避免边界效应并与实验对应，在永磁轨道中央正上方放置拼接好的高温超导块组合。为了简化分析，将超导体块组合等效成长方体。基于上述参数建立高温超导块组合和永磁轨道配对的三维模型，如图11所示。

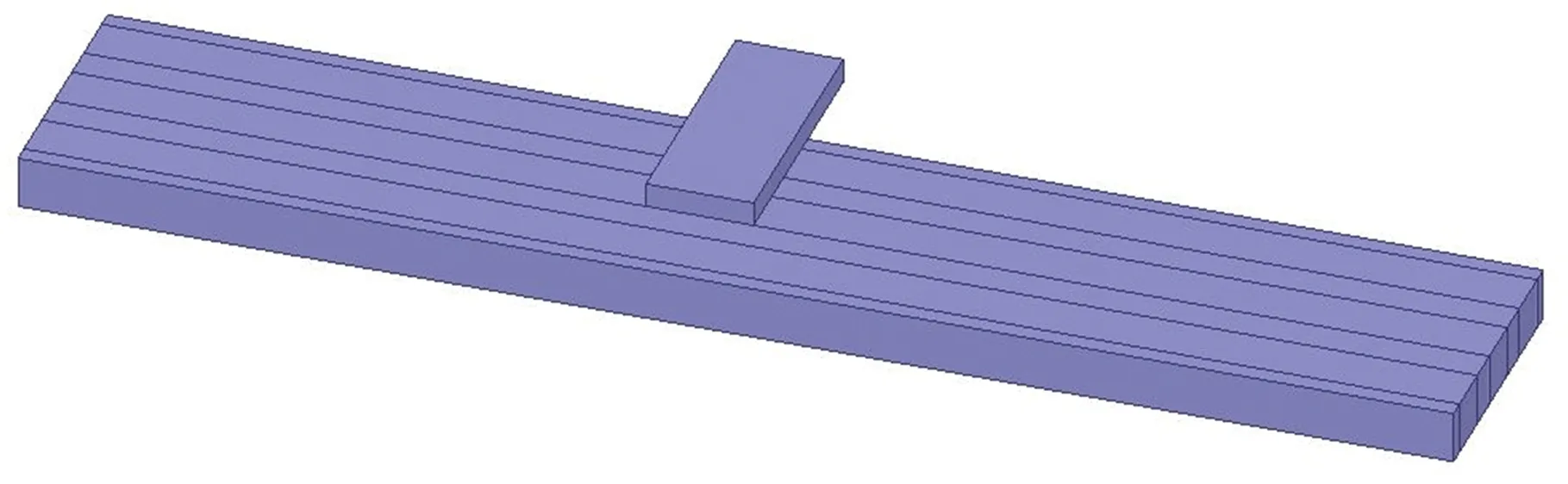
图11 超导体与永磁轨道三维模型

3.3 悬浮力仿真结果分析与讨论

利用Maxwell软件建立的三维模型通过迭代计算得到高温超导块组合的捕获磁场。利用捕获磁场和低相对磁导率的等效处理方法计算高温超导块组合在场冷高度20 mm下的引力和斥力，如图12和图13所示。可以观察到斥力都随着悬浮间隙的增大指数减小，而引力随着悬浮间隙的增大指数增大。

图12 不同悬浮间隙下高温超导块组合所受斥力

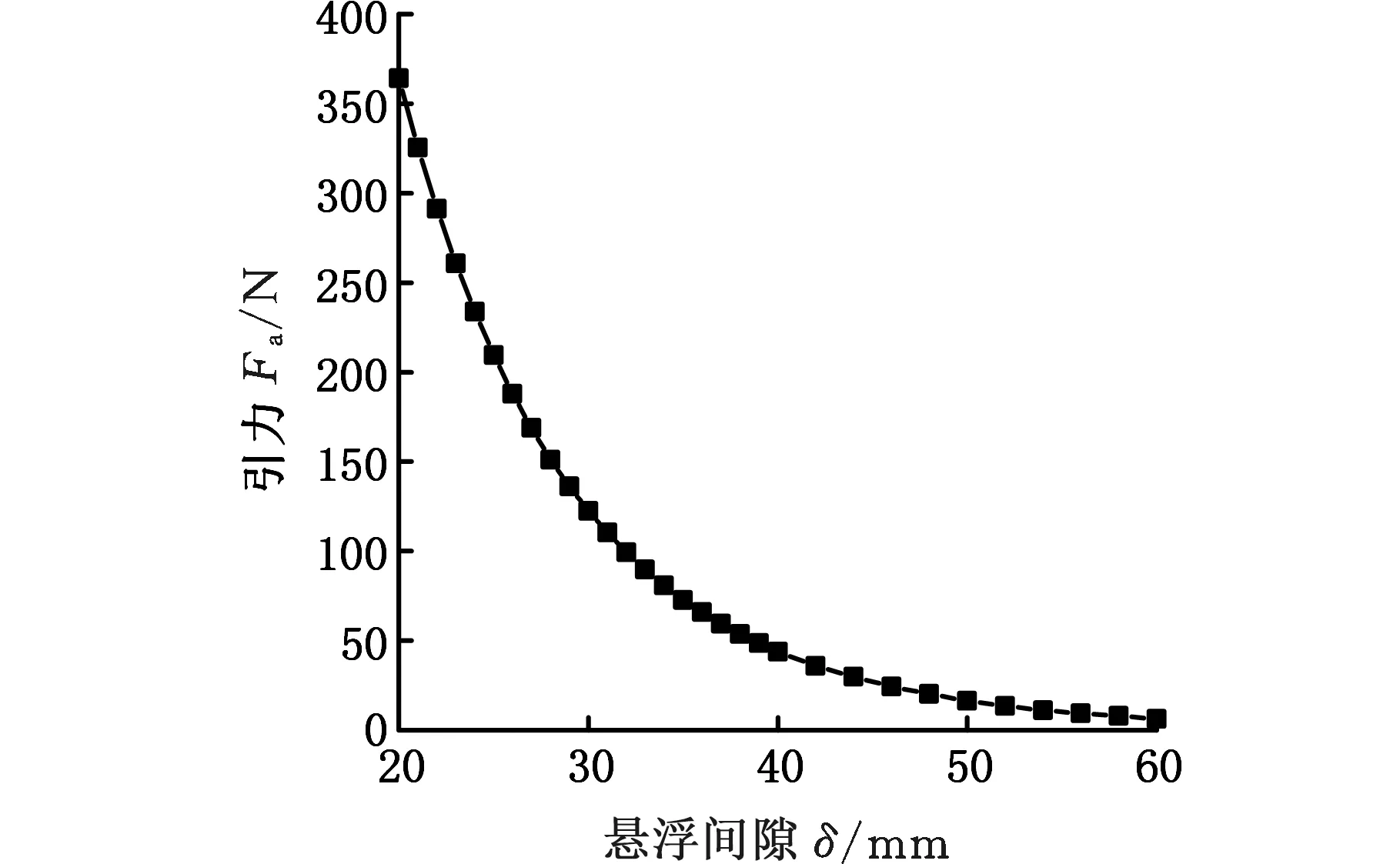
图13 不同悬浮间隙下高温超导块组合所受引力

将斥力和引力叠加求和即可得到高温超导块组合受到的悬浮力，如图14所示。可以观察到悬悬浮力大小随着悬浮间隙的增大先增大后减小，方向为z轴负方向，总体表现为引力，阻碍两者相互远离。

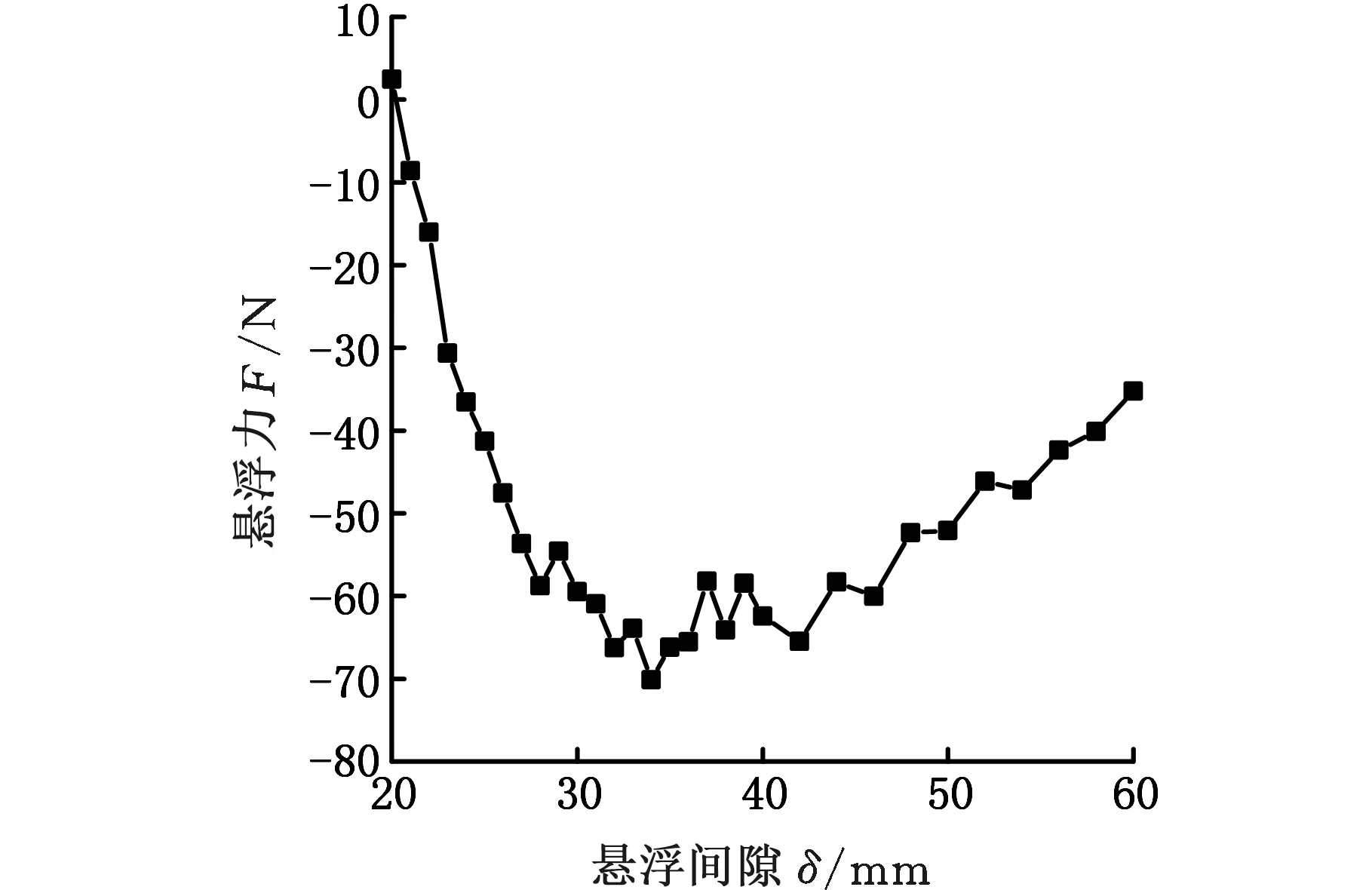
图14 不同悬浮间隙下高温超导块组合所受悬浮力

(a)场冷高度为20 mm

为了验证本文等效处理方法的有效性，将不同场冷高度下悬浮力仿真结果与实验结果进行对比，如图15所示。可以观察到仿真计算的悬浮力与实验测得的悬浮力整体趋势大致相同。当悬浮间隙大于场冷高度时，随着悬浮间隙的增大，悬浮力逐渐增大，增大到一定程度再逐渐减小。同时可以观察到在场冷高度小距离范围内仿真结果和实验结果比较接近。

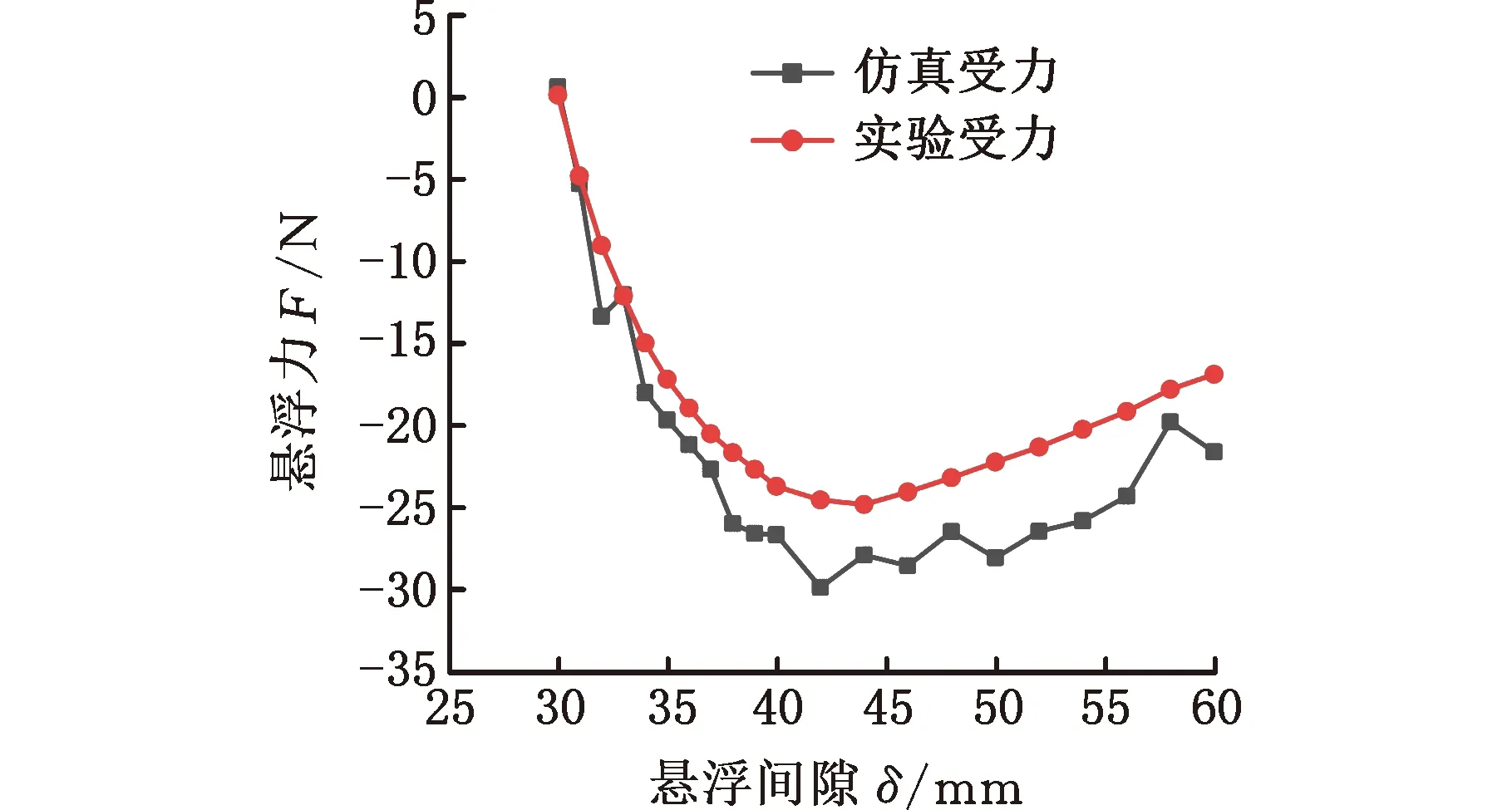
(d)场冷高度为30 mm

由于在实际的高温超导磁悬浮列车运行过程中列车的悬浮间隙需要保持较小的变化，即悬浮间隙离平衡位置不能太远，否则会带来安全隐患，故需着重研究超导体悬浮间隙在场冷高度(平衡位置)附近10 mm内所受的悬浮力特性。以20 mm场冷高度为例，需对比悬浮间隙在20～30 mm内高温超导块组合所受悬浮力的仿真结果与实验结果，如图16所示。

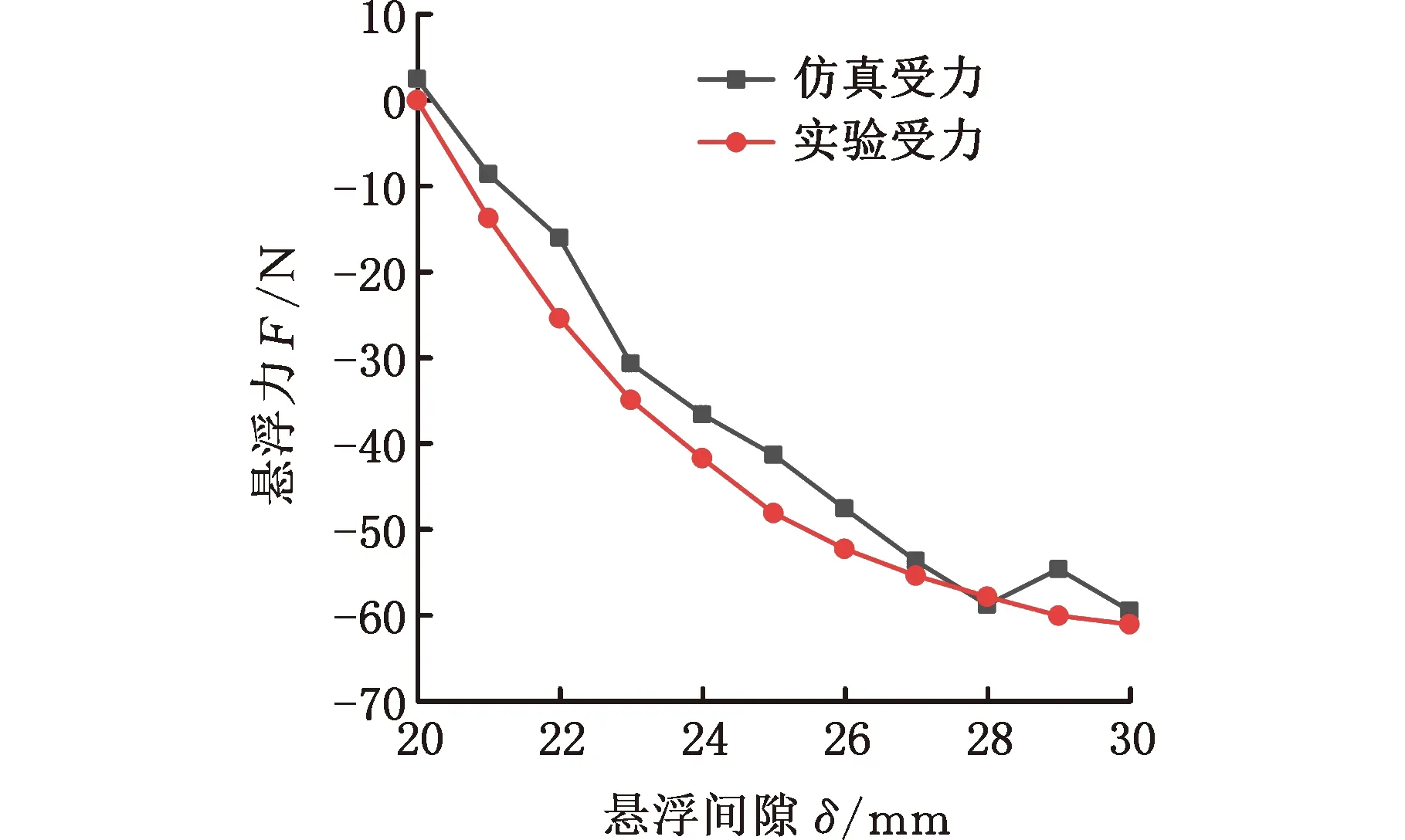
图16 20 mm场冷高度下悬浮间隙20～30 mm的悬浮力对比

由图16可以观察到仿真计算出的悬浮力数据与实验数据相比误差较小，表明采用等效处理方法计算高温超导块组合和永磁轨道间的悬浮力是可行的。该方法可为高温超导钉扎磁悬浮列车的磁轨关系参数优化提供一种简单的计算方法。

4 结论

(1)基于冻结镜像模型提出将高温超导块组合等效处理成低相对磁导率磁体的方法，该方法可以计算其与永磁轨道间的悬浮力。

(2)在固定的场冷高度下，逐渐增加高温超导块组合与永磁轨道的悬浮间隙，悬浮力先增大后减小，且具有明显的磁滞效应。

(3)通过仿真结果与实验结果对比发现，仿真结果与实验结果整体趋势相同，由于高温超导磁悬浮列车的工作特性，在场冷高度附近10mm内的悬浮力仿真结果与实验结果误差较小，验证了所提等效处理方法的正确性。