基于加工误差敏感度与模糊层次分析法的行星滚柱丝杠公差匹配优化方法
吴翰林 魏沛堂 蔡 磊 胡 瑞 刘怀举 杜雪松 朱才朝 刘 浪
1.重庆大学机械传动国家重点实验室,重庆,400044 2.贵州群建精密机械有限公司,遵义,563000
0 引言
行星滚柱丝杠(planetary roller screw mechanism, PRSM)是一种通过丝杠、滚柱、螺母之间多对螺旋曲面啮合将旋转运动转化为直线运动的螺旋传动机构,主要由丝杠、螺母、滚柱、内齿圈和保持架等零件组成。PRSM有着极高的承载能力、传动精度、传动效率、轴向刚度与高速性能[1-2],主要应用于数控机床、航空航天、武器装备及精密机械等领域[3-5]。各行业对PRSM的应用均有较高的精度要求,其关键零部件公差设计是研发过程中的一大难点和关注重点。若公差精度设定过高,加工成本会急剧增大,反之则达不到相应的技术要求。目前,丝杠、螺母、滚柱等关键零部件原始误差因素与PRSM轴向间隙、行程精度的关联规律尚未明确,各误差项公差优化缺乏依据,因此,研究PRSM行程精度与零部件各尺寸、形位公差之间的关联关系及轴向间隙与行程精度之间的关联关系,合理设计公差对PRSM精度保障与提升具有重要意义。
传统的公差优化设计过程中,通常以产品最终质量与制造成本之间折衷平衡作为优化目标。例如,JIANG等[6]考虑产品或结构在实际制造过程中设计变量的不确定性,通过综合考虑目标函数的最优性、设计变量的可制造性和约束条件的可靠性,提出一种基于公差设计的新型区间优化方法。HAN等[7]基于适合线性模型的综合参数与公差设计方法(integrated parameter and tolerance design, IPTD),提出了一种计算机辅助的计算机实验综合参数与公差设计方法,其中输入特性的平均值和公差同时被优化,以使总成本最小。上述公差优化设计方法中所建立的公差优化模型大多是以加工成本最低为目标、以零件或装配体性能为约束的确定性优化模型,在拥有明确的关键公差参数设计理论的情况下能最大程度上减少加工成本、提高加工成品率、提高加工效率,然而当产品本身关键公差设计参数与最终服役性能之间关联关系的理论研究不足时,在无法满足产品性能要求的前提下关注基于加工成本的公差优化方法对工程实际的应用价值并不显著。
相比普通结构件,精密传动机构对零部件加工精度有着极高要求,普通加工生产环境下生产设备所能提供的有限加工精度条件限制了设计精密传动机构时零部件加工精度等级,因此需要引入公差优化理论以对零件公差设计进行修正,以满足一般加工精度下高性能指标要求。杜雪松等[8]提出基于模糊层次分析法的RV减速器公差设计方法,通过构造零件设计参数对传动精度影响程度的敏感系数及加工难易度,提出RV回差分配权重计算方法,实现参数公差分配,并基于分配结果与加工成本函数进行公差优化。潘柏松等[9]建立了考虑齿轮磨损的行星减速器传动精度时变可靠性模型,进行传动可靠性分析与公差优化设计;并建立以加工成本最低为优化目标、传动精度可靠度和齿轮磨损量为约束条件的公差优化设计模型,以序列二次规划法对影响加工成本的设计参数进行优化。上述研究结合实际传动结构形式与特点,建立装配体性能与公差优化模型,提出性能与成本优化匹配方法,实现公差优化理论工程应用。
国内外学者对PRSM关键误差参数与行程误差关系的研究较少。李凯等[10]分析了一种基于PRSM的精密传动机构的传动精度、传动效率两项指标,得到了导程误差、力形变误差和弹性接触形变误差、安装误差、同轴度误差、回程误差、驱动电机误差、支撑轴承和联轴器误差、测量装置误差、控制系统误差、环境因素误差对传动精度的影响程度,推导了传动效率与接触角、螺旋升角的相互关系。MA等[11]对PRSM螺距误差、牙侧角误差、丝杠螺纹同轴度误差、装配误差中偏心误差、偏斜误差、负载变形误差与行程误差的关系进行了研究,得到了空载及负载状态下PRSM行程误差与上述误差因素间的数学关系模型,并通过空载及负载精度实验进行了验证。郑伟等[12]对包括螺距误差、牙侧角误差、螺纹同轴度误差的型面误差、偏心误差、倾斜安装误差、支撑单元顶升误差、热变形误差、弹性变形误差、承载变形误差的变形误差与PRSM行程误差影响因素进行分析,基于各项误差建立行程误差模型并使用行程误差试验台实验验证了模型的有效性。上述研究较为全面地考虑了部分加工、装配、变形误差对行程误差的影响,但较为全面地研究丝杠、滚柱、螺母各关键尺寸公差、形位公差与行程精度之间关联关系的报道较少,无法明确关键公差对行程精度的影响规律,进而无法满足对PRSM公差主动设计的需求。
综上所述,已有相关研究对PRSM加工误差与行程误差的分析较为笼统,缺乏滚柱、螺母加工误差因素对行程误差影响的研究。本文针对公差主动设计需求,对PRSM传动原理及结构进行分析,提出行程精度、轴向间隙与各原始误差因素数学关系模型,计算得到各误差因素敏感性指数;基于三角模糊数的专家评判层次分析法,以5级精度下300 mm行程变动量为指标初步分配PRSM行程精度各误差项公差;基于序列二次规划算法,对影响轴向间隙的各误差项公差进行优化;并通过某型号PRSM进行优化实例数值仿真验证,以证明行程误差计算模型与优化模型的有效性。
1 PRSM行程误差及轴向间隙模型
本文选取对PRSM行程精度和轴向间隙影响较大的公差作为匹配优化设计变量。标准型行星滚柱丝杠典型结构如图1所示,通过螺母、滚柱、丝杠间的螺纹接触实现力的传递,其行程精度直接取决于滚柱-丝杠、滚柱-螺母之间螺纹啮合点位置。因此,本文选取直接影响螺纹间啮合点位置关系的公差,包括丝杠、滚柱和螺母的螺纹中径、螺纹同轴度与螺距公差作为优化设计变量。其中,螺纹中径误差定义为实际测量中径值与理论中径值之差,螺纹同轴度误差定义为螺纹滚道轴心线与两端光轴回转轴心线偏差距离的两倍,螺纹螺距误差定义为实际测量螺距值与理论螺距值之差,如图2所示。
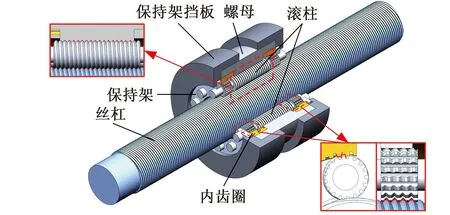
图1 标准型PRSM结构与啮合关系
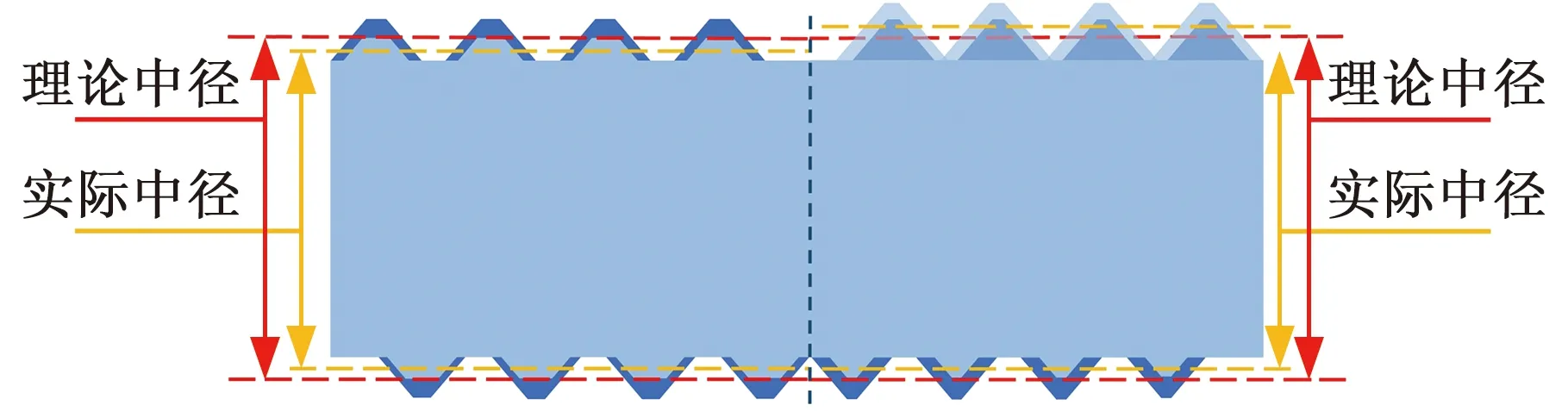
(a)中径误差(左)、螺纹同轴度误差(右)
螺纹同轴度误差定义如图3a所示,黑色外圆面为光轴轮廓外圆面,蓝色外圆面为实际螺纹中径外圆面。为计算由螺纹同轴度引起的行程误差,以丝杠理论轴心线为原点建立参考坐标系(图3b),其中,x轴定义为光轴半径沿水平方向,y轴定义为光轴半径沿垂直方向,光轴轴心线为坐标原点o。
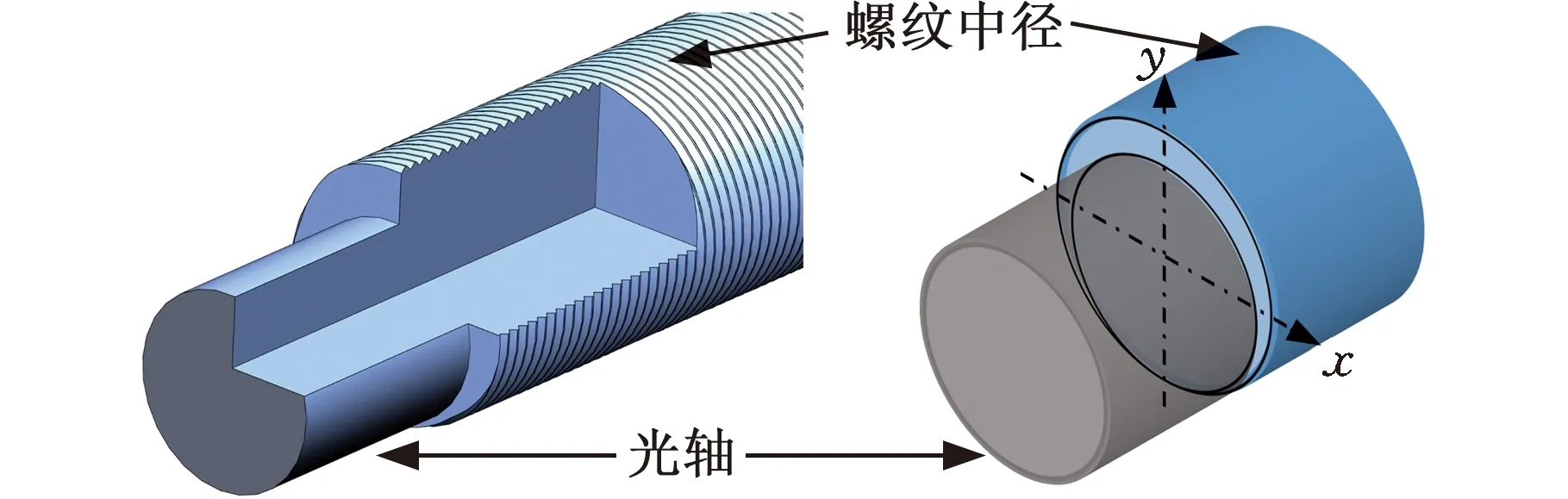
(a)螺纹同轴度误差示意图
如图3b所示,根据定义的x、y轴建立坐标系oxy,同时以螺纹中径圆沿水平方向半径为x轴,沿垂直方向半径为y轴,螺纹轴心线为坐标原点o′建立坐标系o′x′y′。定义角y′oy为螺纹中径圆偏差角θ。灰色实心圆为光轴截面,蓝色实心圆为实际螺纹中径截面,黑色虚线圆为理论螺纹中径截面。在丝杠转角θ下,螺纹啮合点误差Δ即为啮合位置相位角α下,蓝色实心外圆b到灰色实心外圆a处距离ab。有
(1)
其中,R为丝杠转角为θ时原点o距离偏差圆交点的长度,r为黑色虚线圆半径,e为实际轴心线偏离理论轴心线距离。提取R,将式(1)转化为关于R的函数,考虑到R为正值,可写为
(2)
由式(2),在丝杠转角θ下,螺纹同轴度引起的螺纹啮合位置的径向偏差Δ可表示为
(3)
由于标准型PRSM丝杠与螺母牙型角通常为45°,故螺纹同轴度引起的螺纹啮合位置的径向偏差Δ等于其引起的行程误差。由式(3),当丝杠输入转角,即丝杠自转角度为θS时,可计算得到滚柱与丝杠螺母啮合处转角及螺纹同轴度引起的行程误差。
标准型PRSM通常采用多根滚柱与丝杠、螺母配套啮合的方式,增加丝杠-滚柱-螺母螺纹副啮合对数目以增强其承载能力与传动稳定性。但由于滚柱间存在加工误差的区别,存在相互竞争和相互干涉的关系,多滚柱啮合比单滚柱啮合复杂,为了简化PRSM行程精度的计算,本文将多滚柱啮合模型简化为单滚柱啮合模型。图4a为含单根滚柱的标准式PRSM运动示意图,丝杠只存在绕轴线回转的自由度;螺母只存在沿丝杠轴线方向直线运动的自由度;滚柱同时存在绕自身轴线自转与绕丝杠公转的自由度。其中,A点为滚柱起始位置,E点为丝杠自转角度θ后该滚柱的终点位置;dN、dR、dS分别是螺母、滚柱、丝杠的传动节圆直径,称为名义直径或者螺纹中径,dP是滚柱公转轨迹直径;ωS是丝杠旋转角速度,ωR是滚柱绕自身轴线自转的角速度,ωP是滚柱公转的角速度。
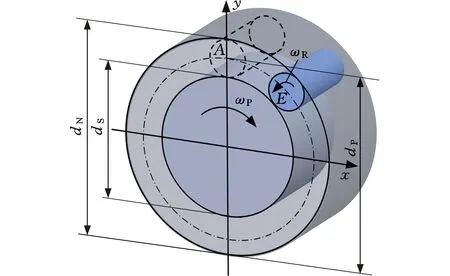
(a)丝杠-滚柱运动示意图
滚柱和螺母螺纹螺旋升角相同,不存在相对位移的情况,其间接触为纯滚动。无外部限位情况下,螺母具有沿丝杠轴向移动及周向转动两自由度,但通常情况下会采用限位装置限制螺母周向自由度,使其直接用于直线推力的传递。标准型PRSM滚柱自转角速度与公转角速度之比为一常值[13],其值决定于丝杠与滚柱螺纹名义中径比km:
km=dS/dR
(4)
如图4b所示,定义θRP为滚柱公转角度,θRR为滚柱自转角度,θRS为滚柱相对丝杠的公转角度,定义顺时针旋转θ为正,逆时针为负,则
(5)
θRR=θRP(km+2)
(6)
θRS=θS-θRP
(7)
基于PRSM运动学原理,定义ΔXR为滚柱螺纹同轴度误差的一半,即由滚柱螺纹同轴度引起的螺纹啮合位置的径向偏差。由滚柱螺纹同轴度引起的滚柱丝杠啮合处行程误差SRep可表示为
(8)
φRR=-(θRR+π)
式中,φRR为滚柱在其与丝杠啮合处相对于同轴度偏心方向的夹角;rS、rR、rN分别为丝杠、滚柱、螺母的名义半径,即螺纹中径的一半。
同理,由滚柱螺纹同轴度引起的滚柱螺母啮合处行程误差NRep可表示为
(9)
φRN=-θRR
式中,φRN为滚柱与螺母啮合处相对于同轴度偏差方向的角度。
同理,可以推导得到相对转角θRS下丝杠螺纹同轴度引起的丝杠滚柱啮合处行程误差Sep:
(10)
式中,ΔXS为丝杠螺纹同轴度误差的一半,即由丝杠螺纹同轴度引起的螺纹啮合位置的径向偏差。
滚柱公转角度θRP下螺母同轴度误差引起的螺母滚柱啮合处行程误差Nep可表示为
(11)
式中,ΔXN为螺母螺纹同轴度误差的一半,即由螺母螺纹同轴度引起的螺纹啮合位置的径向偏差。
联立式(8)~式(11)得到丝杠、滚柱、螺母三者螺纹同轴度误差导致的行程误差:
eP=Sep+SRep+NRep+Nep
(12)
标准型PRSM工作时,滚柱与螺母之间不存在相对轴向位移,滚柱-螺母侧螺距误差造成的行程误差直接取决于螺母与滚柱各自最大单牙螺距误差;滚柱与丝杠之间存在轴向位移,滚柱-丝杠侧螺距误差造成的行程误差取决于滚柱最大单牙螺距误差以及该行程下丝杠累积螺距误差。
由螺距误差引起的行程误差为
(13)
式中,EPN为螺母最大单牙螺距误差;EPR为滚柱最大单牙螺距误差;EPST为丝杠累积螺距误差;Kp为单牙螺距误差与累积螺距误差之比,在300 mm螺纹全长上5头螺纹的Kp取值范围通常为2~3,根据实际加工经验,取Kp=23/8。
实际检测过程中,中径测量误差为综合误差,反映了牙型角误差、螺距误差、中径误差的累积,单独的中径误差仅仅反映了未啮合前PRSM内部的初始间隙,对啮合后传动精度几乎不会造成影响,因此在行程误差模型中暂时不予考虑,而是在轴向间隙模型中予以考量。
联立式(12)、式(13),得到总行程误差目标函数:
EP=Sep+SRep+NRep+Nep+EPt
(14)
由式(12),丝杠、滚柱、螺母螺纹同轴度误差引起的行程误差为单向螺纹牙啮合状况下的误差,即螺纹同轴度误差引起轴向间隙的变化量2倍于行程误差变化量。根据螺纹同轴度误差定义,轴向间隙值将随着误差值的增大而减小。根据螺纹中径误差定义,轴向间隙随着丝杠与滚柱中径误差的增大而减少,随着螺母中径误差的增大而增大。就螺距误差而言,其值将1∶1反映到引起的轴向间隙变化量,即螺距误差值为轴向间隙值。轴向间隙数学模型如下:
Sa=-2eP-ΔS-2ΔR+ΔN+EPN+2EPR+EPS
(15)
式中,Sa为轴向间隙;ΔS为丝杠中径误差的一半;ΔR为滚柱中径误差的一半;ΔN为螺母中径误差的一半。
为验证所建的PRSM行程精度及轴向间隙模型的正确性,将本文方法与文献[11]提出的基于矩阵坐标变换方法建立的PRSM传动误差模型进行对比。采用与表1相同的PRSM参数,并取相同的丝杠、滚柱、螺母螺纹同轴度、螺距及中径误差,采用上述两种方法对丝杠旋转一定角度下的行程精度进行计算,结果如图5所示,可以看出两者计算得到的行程误差偏差在0.5%以内,初步验证了本文建立的行程精度模型的正确性。
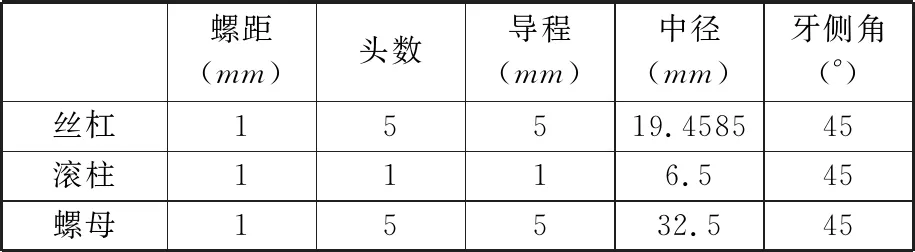
表1 PRSM结构参数
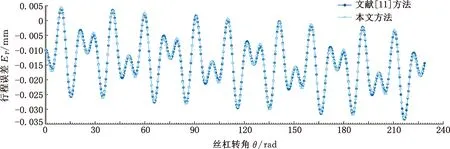
图5 PRSM行程误差模型对比验证
采用图6a所示的行星滚柱丝杠空载传动精度试验台,对表1所示结构参数的PRSM进行空载传动精度测试,测试有效行程长度为80 mm。PRSM行程精度试验结果和模型预测值对比如图6b所示,行程精度预测模型中采用各关键零件实测加工误差作为输入。经对比,PRSM行程精度模型预测结果和行程精度试验结果的有效行程变动量Vu分别为12.2 μm、15.28 μm,预测值与实际值误差为20.16%,考虑到试验过程中随机误差的影响,误差在接受范围内,验证了多滚柱啮合模型简化为单滚柱啮合模型的可行性和所建PRSM行程精度模型的正确性。

(a)空载传动精度试验台
2 PRSM关键公差分配方法
PRSM公差的合理分配主要取决于两方面[8]:①设计参数误差对行程精度的敏感度。敏感度反映设计参数误差对行程误差影响程度,敏感度越大,影响程度越大,公差分配时许用误差越小,加工控制越严格。②设计参数加工难易度。不同零件即使相同精度等级其加工难易度亦不相同,需对加工难度更大的设计参数分配较大的公差值宽度,以提高加工成品合格率。
基于所建的PRSM行程误差与轴向间隙模型,开展行程误差与轴向间隙误差敏感性分析,提出一种基于参数灵敏度分析及加工难易度综合权系数的PRSM关键公差分配方法,分配目标精度等级下行程误差至各设计参数公差,实现零件公差的初步分配,技术路线如图7所示。通过建立行程误差数学模型与轴向间隙数学模型,对关键公差进行敏感性权系数求解,同时基于三角模糊数的专家评判层次分析法求解各公差加工难易度权系数。综合加工难易度权系数与敏感性权系数,对各公差许用行程误差进行分配,若校验公差分配结果得到的行程误差值符合要求,则基于序列二次规划算法以轴向间隙对公差进行优化。最后通过优化前后行程误差与轴向间隙结果比对验证公差分配优化模型的正确性。
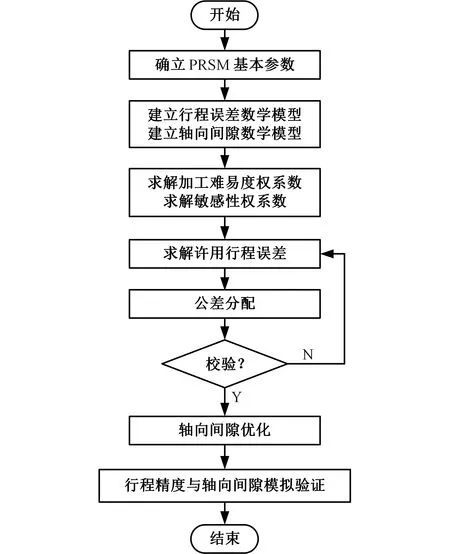
图7 公差分配优化流程图
2.1 行程误差敏感性分析
为建立关键零件公差与PRSM行程误差的关联关系,需对上述模型涉及到的螺距公差、中径公差、螺纹同轴度公差进行敏感性分析,以满足基于行程精度与轴向间隙对公差进行主动设计的需求。
精密传动行程精度的影响误差大致分为三类:周期性系统误差、随机误差、非周期性系统误差。就PRSM而言,其行程精度的周期性误差主要由丝杠、滚柱、螺母螺纹同轴度原始误差引起,而非周期性误差则由丝杠、滚柱、螺母中径误差及螺距误差引起。随机误差是温度、湿度、环境因素引起的,本文暂未考虑。
设PRSM各误差因素x=(x1,x2,…,xk)为设计变量,令Δθ(x)=f(x),则目标函数对设计变量的灵敏度为[14]
基于第2节各关键误差因素对行程误差关系模型与上述敏感性计算公式,对PRSM中各误差因素的敏感性指数进行计算,结果如图8所示。可以看出,所有误差因素与行程误差均为正相关,其敏感性指数从大到小依次为:丝杠螺距(2.8750)、滚柱螺距(1.0000)、螺母螺距(1.0000)、丝杠螺纹同轴度(0.9800)、螺母螺纹同轴度(0.4750)、滚柱螺纹同轴度(0.0585)。滚柱同轴度敏感性指数小于0.1[14],故不需考虑滚柱同轴度误差。
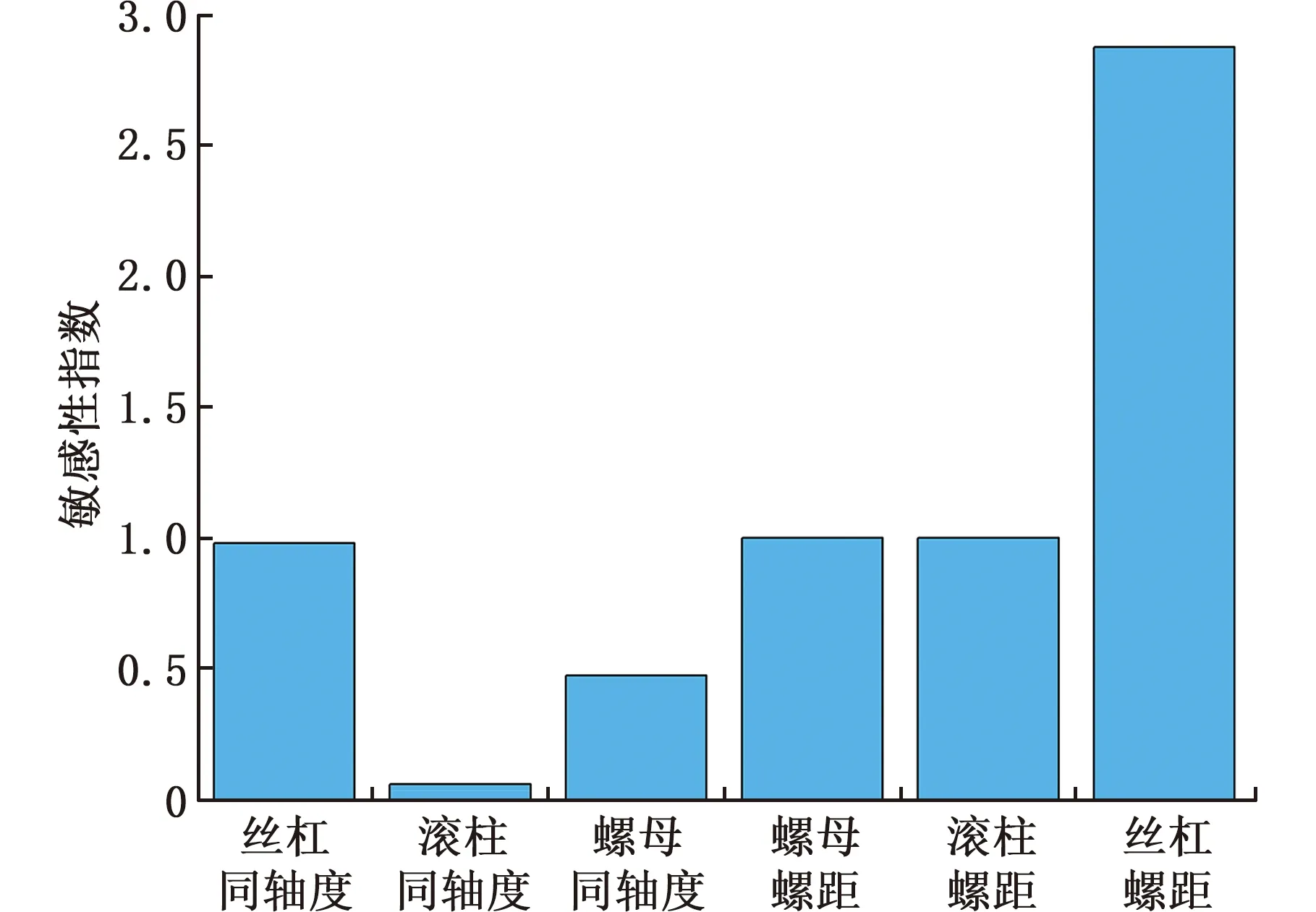
图8 行程误差敏感性指数直方图
2.2 轴向间隙敏感性分析
PRSM轴向间隙反映了运动过程中各构件相对位置关系,轴向间隙与行程精度呈负相关,为同轴度误差、螺距误差与中径误差共同作用结果。因此,需对轴向间隙进行敏感性分析以满足正常装配需求,实现PRSM轴向间隙主动设计,避免因干涉产生的装配误差对装配体传动性能的影响。
如前所述,因中径误差对行程精度无直接影响,但对轴向间隙有显著影响,因此,本文基于灵敏度计算公式,对中径误差ΔS、ΔR、ΔN进行轴向间隙敏感性分析,得到敏感性指数从大到小依次为:滚柱中径误差(-4)、丝杠中径误差(-2)、螺母中径误差(2),其中丝杠与滚柱中径误差与轴向间隙为负相关,由于螺母为内螺纹,故其中径误差与轴向间隙为正相关。
2.3 关键零件加工难易度评估
为了评估PRSM关键零件加工难易度,本文采用Delphi法,由专家对在上层准则影响下同一层次的指标进行两两重要性比较,并利用三角模糊数构造模糊判断矩阵[15]。所构造的模糊判断矩阵中[l,m,u]取值依据1-9标度法[16],见表2,在三角模糊数中,中值m为专家给出的两指标相对重要程度。模糊评判区间下界l和上界u可根据专家对判断的模糊程度加以确定,u-l越大,表示专家的判断越模糊,u-l越小,表示专家的判断越清楚。当u-l=0时判断是明确的,这时,

表2 1-9标度法及其含义[16]
u=m=l与一般意义下的判断标度值相同。
通过专家评审,得到PRSM设计参数加工难易模糊矩阵,见表3。其中,Z1为丝杠螺纹同轴度;Z2为滚柱同轴度;Z3为螺母螺纹同轴度;Z4为螺母螺距;Z5为滚柱螺距;Z6为丝杠螺距。

表3 PRSM设计参数加工难易度模糊判断矩阵
对判断矩阵构造模糊评价因子矩阵E,计算公式如下:
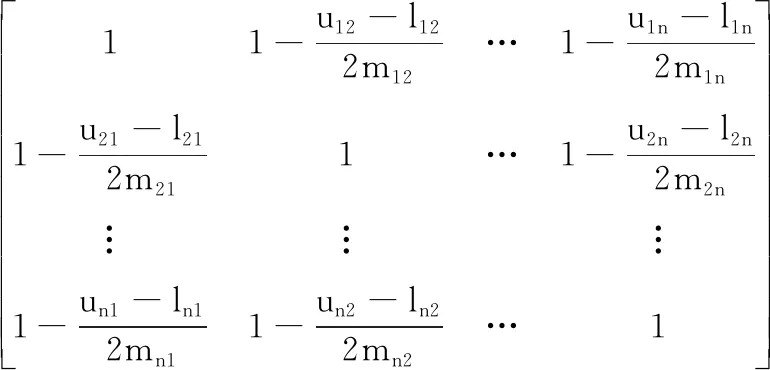
式中,sij为标准差率,反映专家评判的模糊程度,其值越大,模糊程度越大,反之亦然。
调整判断矩阵Q可表示为
式中,矩阵M为判断矩阵中所有三角模糊数中值mij组成的矩阵。
将调整判断矩阵Q按列转换为对角线为1的判断矩阵,记为判断矩阵P,则P=(Pij)n×n,且满足Pij=1/Pji。
用相容矩阵分析法对矩阵P进行变换,得相容矩阵R=(rij)n×n,R满足一致性条件rij=rikrkj(i,k=1,2,…,n),且rii=1,rij=1/rji。rij按下式进行计算
计算评估指标的权重ωi:
对表3进行计算分析,得到各误差参数加工权重系数,见表4。结果表明,加工权重系数最大的为丝杠螺距公差(0.9987),螺母螺纹同轴度(0.1214)加工权重系数次之。相对而言,丝杠螺纹同轴度和螺母、滚柱、丝杠螺距的加工权重系数非常小。这主要是由于PRSM丝杠螺纹长度远长于螺母、滚柱螺纹,且通常为多头螺纹,其加工精度只能依靠加工机床本身精度保证,故加工难度远远大于其他尺寸公差、形位公差。同理,螺母与丝杠同为多头螺纹,但螺纹长度短于丝杠,而滚柱为单头螺纹,螺纹长度略短于螺母螺纹长度。与此同时,螺纹同轴度误差可通过对装夹装置的重新设计以及加工工艺的优化得到改善,因此它作为可人为控制的误差因素,加工权重低于螺距误差因素。由表4得到的不同误差参数加工权重系数排序与基于实际加工经验与理论得到的排序结果一致,初步验证了加工权重的正确性。
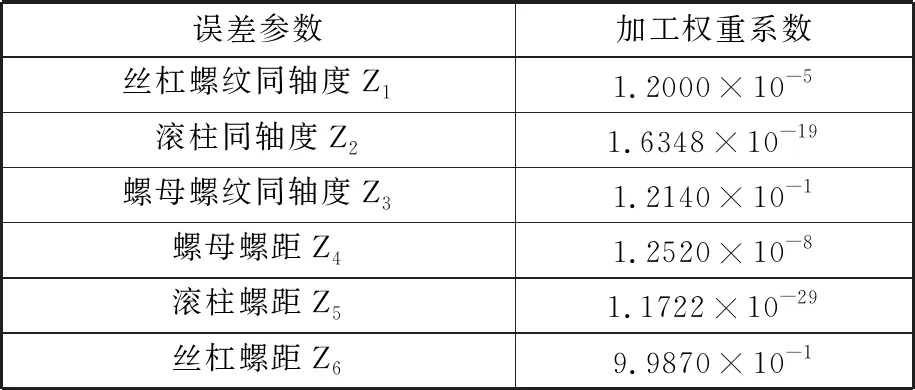
表4 误差参数加工权重系数
2.4 关键公差综合分配权重
基于PRSM行程精度和轴向间隙参数灵敏度分析以及计算得到的加工难易度综合权系数,采用PRSM关键公差综合分配权重计算方法,将目标精度等级下行程误差分配至各设计参数公差。
考虑到加工难易度极端值的不利影响,本文采用平方平均数作为敏感性指数及加工难易度综合后的权系数的计算方法,使其结果较为稳定合理。建立的各参数权重表达式为
(16)
其中,ωβi为第i个误差参数的加工难易度权系数;ωαi为第i个误差参数的敏感性权系数,可表示为[17]
(17)
式中,Si为误差参数的敏感性指数,参数敏感性指数越高,相应敏感性权系数越小,进而许用行程误差越小。
采用式(16)、式(17)由丝杠、滚柱、螺母螺纹同轴度以及丝杠、滚柱、螺母螺距误差因素敏感性指数计算得到的敏感权系数见表5。
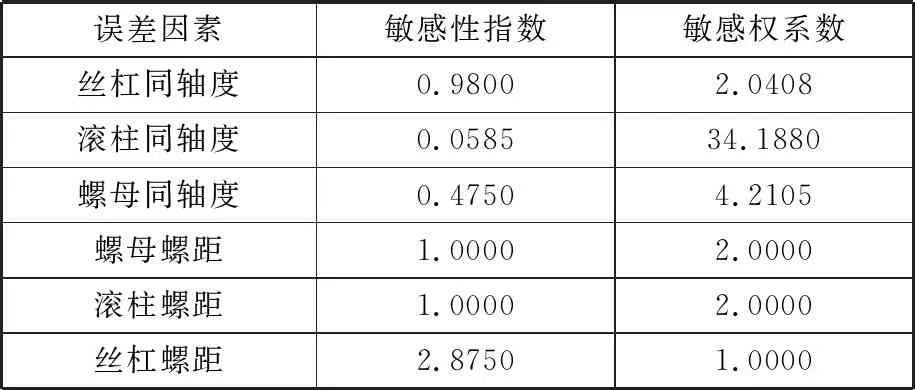
表5 敏感性计算结果
将行程误差按照权重系数分配给各关键公差:
epi=ωiep0
(18)
式中,epi为各关键公差分配得到的行程误差;ep0为总行程许用误差。
由误差敏感性权系数及零件加工难易度权系数,经式(18)计算得到的PRSM关键公差分配权重见表6。
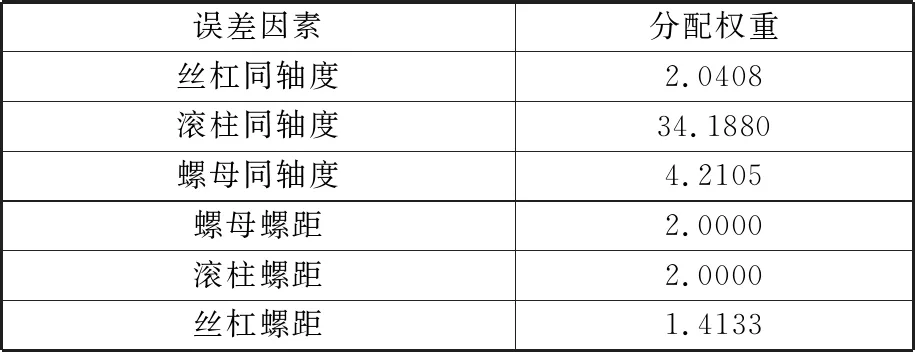
表6 关键公差分配权重
基于计算得到的分配权重,根据行业标准JBT12604—2016对行程精度的定义,对PRSM 5级精度下300 mm行程变动量V300进行误差分配,代入式(14)对分配后的行程误差进行求解,得到的各关键公差分配比例与公差带宽度见表7。
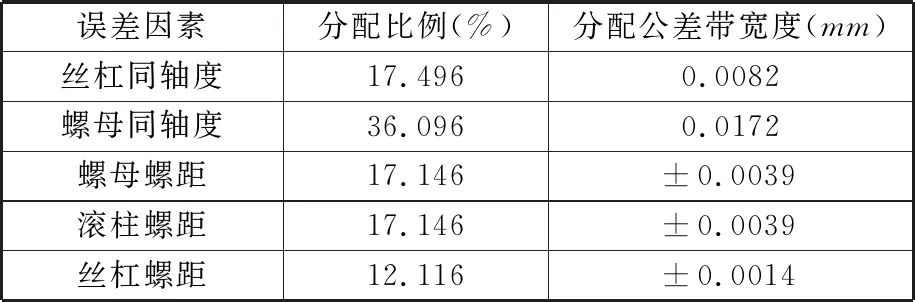
表7 关键公差分配结果
综合表5~表7得到PRSM公差设计结果,见表8。
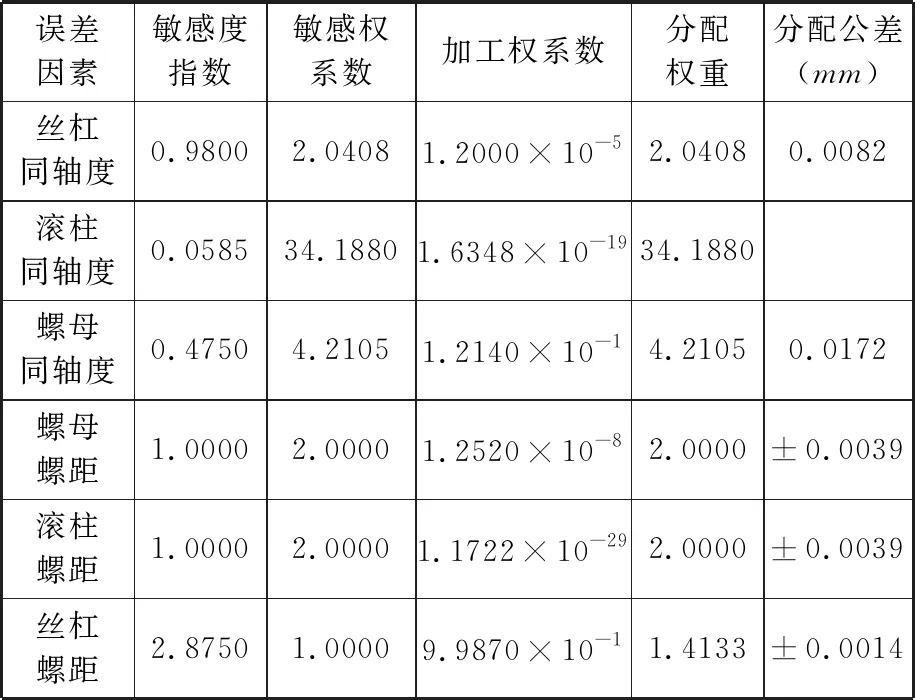
表8 PRSM关键公差设计结果
3 PRSM关键公差优化方法
PRSM运行过程中其轴向间隙随丝杠自转发生周期性变化,当完整周期中轴向间隙最小值为负时,发生螺纹副干涉现象,影响运动稳定性、精度保持性和服役寿命。由第2节,因中径误差对行程精度无直接影响,但对轴向间隙有显著影响,因此设计时以PRSM运行完整周期内避免干涉为优化目标,即minF(xi,xj)=0,优化中径公差上下限,确保公差带范围PRSM正常运转。
基于表8公差分配结果,对PRSM丝杠、滚柱、螺母中径公差进行优化,以满足行程误差要求的同时满足轴向间隙要求。
3.1 目标函数及约束条件
以式(15)作为行星滚柱丝杠轴向间隙目标函数,以滚柱、丝杠、螺母中径误差精度等级作为约束条件:
式中,xi,i=1,3,5、xj,j=2,4,6分别为丝杠、滚柱、螺母中径的上极限偏差值与下极限偏差值;Δyi,i=1,3,5、Δyj,j=2,4,6分别为丝杠、滚柱、螺母中径上极限偏差值与下极限偏差值初始取值的幅值,其值取决于实际加工设备提供的一般水平加工精度条件;a、b分别为不同加工精度等级中径公差带宽度下限与上限,可查询GB/T 1800.1—2009标准得到[18]。
本文选择IT6级精度作为尺寸公差带,根据尺寸精度等级,得到丝杠中径误差的约束条件为
滚柱中径的约束条件为
螺母中径的约束条件为
3.2 优化实例
本节以标准型PRSM为例,结构参数见表1。根据第2节建立的轴向间隙数学模型和3.1节建立的约束条件构造适应度函数如下:
minF(xi,xj)=-2EP-ΔS(xi,xj)-
2ΔR(xi,xj)+ΔN(xi,xj)+EPN+2EPR+EPS
基于2.4节公差分配结果,考虑PRSM中径优化为非线性优化问题,采用收敛性好、计算效率高、边界搜索能力强的序列二次规划算法(sequential quadratic planning,SQP)对丝杠、滚柱、螺母中径施加3.1节建立的约束条件,并利用MATLAB中SQP算法对轴向间隙适应度函数进行计算,得到规定加工精度等级下丝杠、滚柱、螺母中径的最优解,见表9。设计参数的对比见图9。
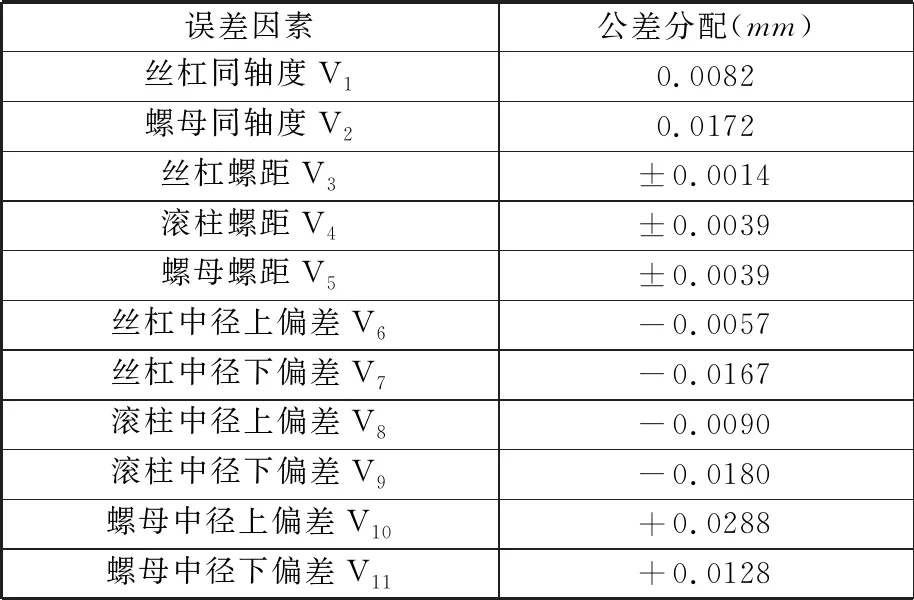
表9 公差分配优化结果
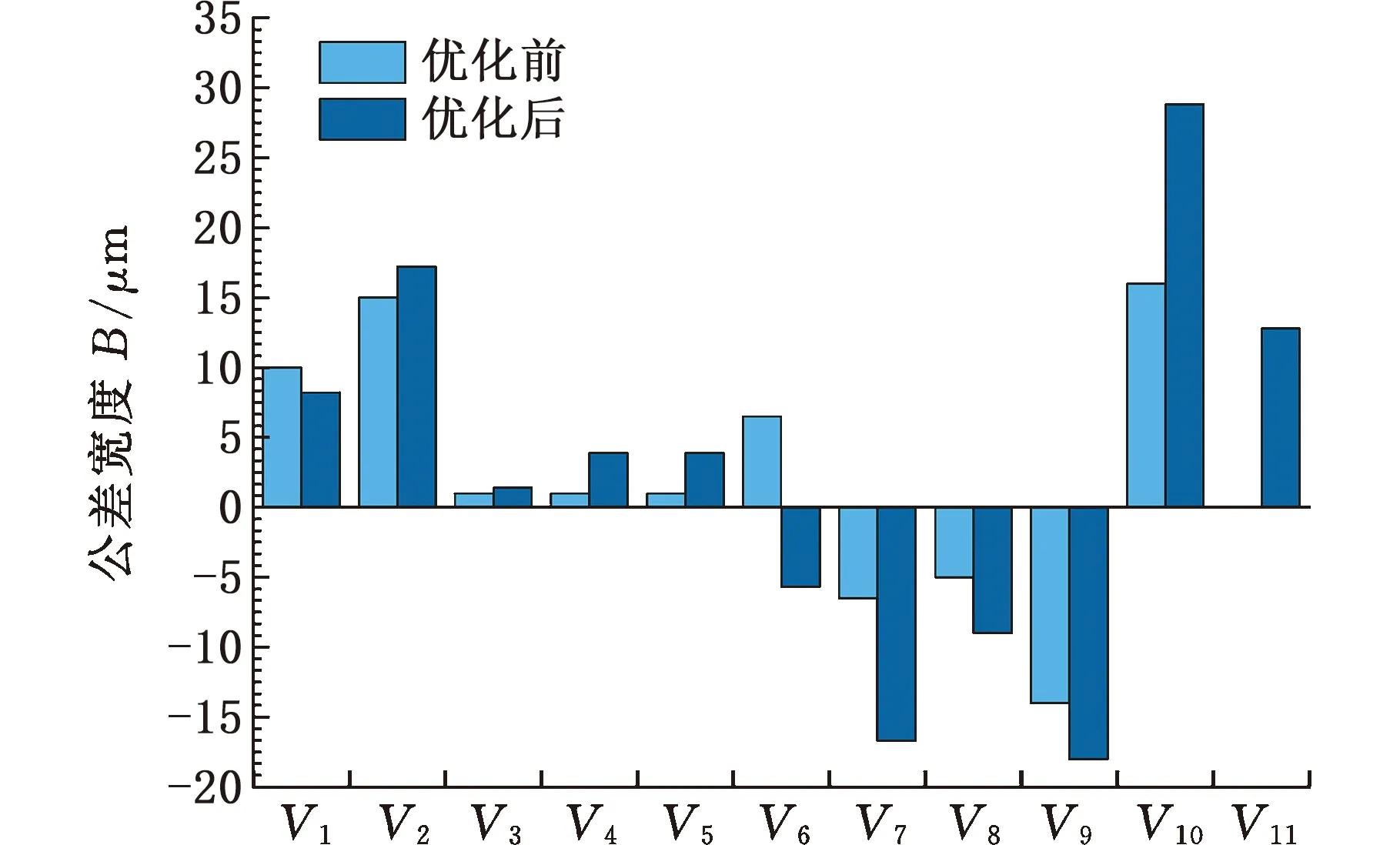
图9 设计参数对比
优化后PRSM行程精度随丝杠转角变化的关系图如图10a所示,轴向间隙随丝杠转角变化的关系如图10b所示。关键公差的公差带宽度与优化前相比平均扩大65%,优化后各公差参数上下偏差及公差带宽度分配更为合理,实现了PRSM关键零件加工精度IT6-7级标准公差精度等级下,行星滚柱丝杠V300满足5级行程精度指标,即300 mm行程变动量控制在23 μm以内。同时,经优化后完整周期内轴向间隙最小值由-25 μm变为0,有效避免了螺纹干涉。本文方法极好地平衡了行程精度与轴向间隙,可有效避免局部公差参数设计不合理导致加工难度过大的问题,提高了零件加工可行性、经济性,可为PRSM的理论设计与工程加工提供支撑。
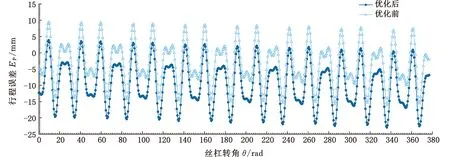
(a)优化前后行程精度
4 结语
(1)丝杠、滚柱、螺母螺纹同轴度误差和螺距误差与行程误差均为正相关,其中敏感性系数最大为丝杠螺距误差,其次为滚柱、螺母螺距误差、螺母螺纹同轴度误差且三者较为接近。丝杠、滚柱中径误差与轴向间隙为负相关,螺母中径误差与轴向间隙为正相关,其中敏感性系数最大为滚柱中径误差,其次为丝杠中径误差、螺母中径误差且两者相等。
(2)基于三角模糊数的专家评判层次分析法求解零件加工难易度权系数,获得各公差加工难易度大小关系。加工权重系数最大的为丝杠螺距公差,螺母螺纹同轴度加工权重系数次之。
(3)算例表明,经优化后在保证V300 5级精度的前提下,对各关键公差进行了放宽,公差带宽度平均增加65%,提高了关键零部件的加工可行性、加工合格率和经济性;同时优化后完整周期内轴向间隙最小值由-25 μm变为0,避免了极端情况下因螺纹啮合干涉导致的无法正常运转。

