应用DCNLP的电机输出力矩受限下机械臂能耗分析*
彭见辉,李佳玉,陈军杰,彭展恒
(东莞理工学院城市学院,东莞 523419)
0 引言
随着我国净增人口的快速减少,人口红利优势正在消失,人力成本逐渐增大,制造业面临着转型升级的迫切压力,在各领域推进机器人换人显得尤为必要[1],工业机械臂在各行业的应用已连续七年排在世界第一大产业[2]。电动机作为影响电机驱动型机器人生产成本、工作精度的主要因素之一[3],其输出力矩范围直接决定了电机的价格,若电机力矩范围选择不当会导致电机工作电流变化较大,引起机械臂产生振动、冲击,影响其性能及工作精度,如何选择力矩范围合适的电机对保持机械臂的工作性能、降低采购成本及工作能耗至关重要。
庞哲楠等[4]采用多种控制器相结合的方式,有效抑制了漂浮空间中机器人的柔性振动;梁作昊[5]采用了模糊自适应动态面的控制方法,以辅助信号限制实际扭矩受限对机械臂的影响;高兴泉等[6]针对输入受限倒立摆的控制问题,采用输入约束下的T-S模糊模型,达到了其保代价的控制要求;钱美容等[7]提出了一种输入力矩受限下机械臂的反演滑模控制,但仅限于2自由度机械臂的简单轨迹控制;高欣等[8]采用粒子群算法,有效降低了空间机械臂运动过程中的关节力矩均值,并获得了其最小运行轨迹。以上研究主要针对能源受限的空间机械臂或自由度较少的机械臂,针对生产中应用的多自由度机械臂,如何在确保机械臂顺利完成工作的同时,尽量限制各关节输出力矩的范围,抑制电机振动,对降低采购成本、减小工作能耗、延缓机构磨损、提高工作寿命具有重要意义。
目前以直接配置结合非线性规划的方法(DCNLP)用来解决机器人的相关问题还处于探索阶段[9-10],尤其在优化机械臂关节电机输出力矩范围、减缓电机振动方面的探究仍处于空白。本文采用直接配置和非线性规划方法[11-12]解决各关节不同力矩输出范围下,机械臂最优控制下的两端点边界值问题(TPBVP)和最优能耗问题,确定机械臂完成相同工作关节电机的临界力矩值,并对各关节输出力矩进行频谱分析,为机械臂选择合适的力矩范围,以最优能耗平稳的完成工作提供重要参考。
1 机械臂模型的建立
1.1 机械臂数学模型
本文以5连杆机械臂为研究对象,其结构简化如图1所示,其中基座定义为连杆0,不包含在本文所要研究的5个连杆之内,连杆1的转动轴垂直地面,其上坐标系为基坐标系,连杆2、4上的关节运动形式为上下转动,连杆3和连杆5上的关节运动形式为左右转动。

图1 五连杆机械臂模型
以D-H矩阵表示两个相邻连杆坐标系[13]、各连杆相对基坐标系的相对位移。根据图1定义iri为在连杆i上固定点,如式(1)所示,并以关于第i个连杆坐标系的齐次坐标表示,其中将第i个坐标系与基坐标系相关联的坐标变换矩阵0Ai定义如式(2)所示。
0ri=0Ai·iri
(1)
0Ai=0A11A2…i-1Ai
(2)
相邻连杆的变换矩阵如式(3)~式(7)所示。
(3)
(4)
(5)
(6)
(7)
1.2 机械臂动力学方程
假设各连杆均为刚性且细长杆,同时定义各连杆质量mi=1 kg、长度Li=1 m。以拉格朗日-欧拉方程[14]构建5连杆机械臂的动力学方程式:
(8)

(9)
式中,g=[0 0 -9.81 0]为重力加速度的矢量表达式;mi、Li为机械臂第i连杆的质量、长度;Ji为各杆转动惯量矩阵,具体如式(10)所示。
(10)
Uij为自定义矩阵,其形式如式(11)所示:
(11)
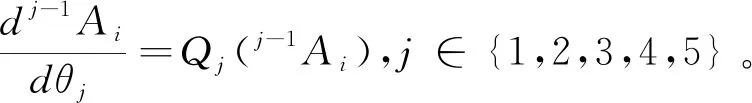
当机械臂连杆数n>3,上式(8)、式(9)的变换推导十分繁琐[15],本文以Mathematica的符号语言编程法(symbolic language)推导连杆数n=5时的式(8)并变换为式(12):

(12)
将式(12)进一步变换为:
(13)
式(13)是用10个状态变量x(t)=[θ1(t),ω1(t),θ2(t),ω2(t)…θ5(t),ω5(t)]表述机械臂关节动力学的10个非线性一阶微分方程,至此,再以符号语言编程法进行式(13)的完整推导。
2 最优控制理论及直接配置非线性规划
2.1 最优控制理论
(1)最优控制理论。最优控制采用的系统方式为:

(14)
式中,x(t)为状态变量;u(t)为控制项,其部分的初值和终值已给定。
某些状态变量在tf时,必须维持在一定的关系式下,据此上述给定的终值将被收录在终端限制向量Ψ。为了找到最优化控制u*(t),以满足初值及终值控制项Ψ,并且将成本函数J降到最小值,则将J值定义如下:
(15)
式中,φ为纯量方程,只和x(tf)、tf有关。
(16)

为推导方便,再定义一个纯量方程式H:
H=L+λT·f
(17)
同时令
Φ=φ+vT·ψ
(18)
式(18)联结终值φ及最后限制ψ,vT联结φ及ψ。
总之,美国政治家在面对具体问题时,总要把外交决策置于精明的利益计算之上,任何时候都决不会脱离利己为先的盘算,这是美国外交的“现实主义”一面;但是,美国外交同时也要处理好现实利益与自由主义价值认同之间的关系,这是所谓“理想主义”一面。毫无疑问,现实主义国家利益观与自由主义价值认同感的有机结合,才是国际外交的“美国风格”。忽视相对独特的自由主义观念对美国外交的影响,显然是片面的。


(19)
(20)
(21)
xi(t0)、xj(tf)、λk(tf)
(22)
(23)
式(19)、式(20)的边界值分别在起点、终点给定,甚至有时给定的并不全,式(22)各项值均已给定,最优控制项u*(t)是最优条件下x(t)、λ(t)的函数,至此机械臂的最优控制演变成两端点边界值问题,此问题是非线性的,难以求解。
采用间接逼近方法[16]是对未给定的x(t)、λ(t)设下猜测值,并将猜测值代入式(19)和式(20),再进行积分,但积分的结果往往无法满足式(22)和式(23)。多数研究致力于不断改进猜测方式,但不能保证迭代结果一定收敛。
2.2 直接配置与非线性规划
本文不再使用间接逼近法,改用直接配置和非线性规划的方法(DCNLP)以解决上述问题,并实现机械臂工作过程中的最优能耗控制。直接配置法通过使用非线性规划技术将两端点边界值问题转变为参数优化问题,打破了数值计算的僵局。DCNLP将连续的两端点边界值问题中的工作用时[t0,tf]分割为n段,则会出现n+1个时间分割点,分割后每小段时间长度为T=ti-ti-1,令S=(t-ti)/(ti-ti-1),则S∈[0,1],如图2所示,在每个分割点上分配状态变量的值为Xi,在两个分割点间采用一个三次多项式如式(24)所示。
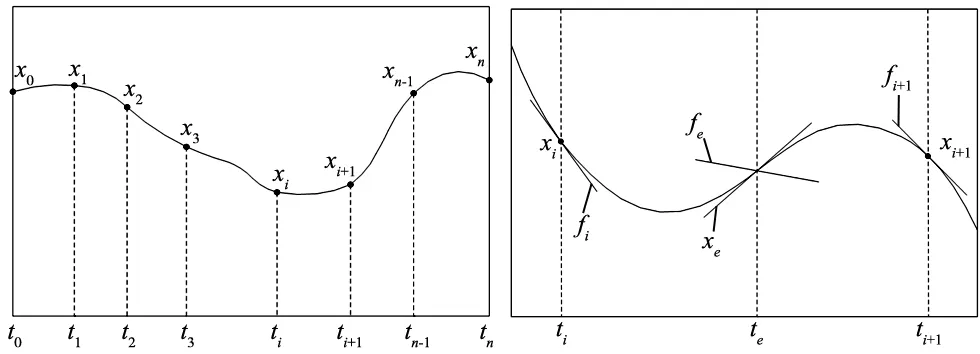
图2 时间段分割方案图3 Simpson在第i段中的系统限制方程
x=C0+C1S+C2S2+C3S3
(24)

将式(24)微分,以上4个式子代入,并在0和1之间计算出其值,得到:
(25)
对式(25)变形,利用其逆矩阵得到C1、C2、C3、C4的值:
(26)
在分割的每个小时间段的中点计算x及x′,其中在每个小时间段中点处S=0.5,推导出式(27)和式(28)。
(27)
(28)
(29)
式(13)中包含10个一次状态差分方程,将机械臂工作用时分成128段,共存在1128个系统限制方程Δ,并在最终收敛时限制方程Δ均为0。
以直接配置结合非线性规划的方法对x[k]在n+1个节点位置开始猜测,并以初始猜测、各小段时间中心点的τ[k]进行迭代计算。在进行迭代计算前,应先提供一个与∂Δ/∂X的雅克比矩阵十分相似的带状矩阵,如表1所示。

表1 限制方程的JACOBIAN矩阵
2.3 能耗指标函数J的设定
本文以机械臂完成动作的各关节最小力矩平方和之值作为最优控制问题的性能指标,设定其能耗指标函数J的方程:
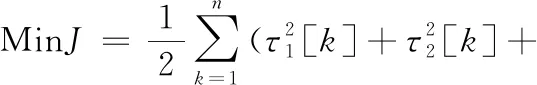
(30)

3 仿真及结果分析
3.1 初始条件设定
本文以五连杆机械臂工作过程进行仿真,为便于对5个关节力矩进行快速傅里叶变换(FFT),将工作用时tf设定为1 s,并切割成128份等长的时间段,共129个切割点,其中第65点为目标工件的预定点,将各关节在第1点的θ[1]、ω[1],第65点的ω[65],第129点的θ[129]、ω[129]分别设定如下,同时为提高机械臂在抓取目标物前后的平稳性,将第65点前后各6点的5个关节角速度ωi[k]限制在±0.1 rad/s以内,另外工件坐标设定在P2处,θ[1]、θ[129]处机械臂末端坐标均为P1,将机械臂工作过程中的5个关节输出力矩范围Bm限制在[-Bm,Bm]内,各初始参数设定具体如下:
θ[1]=[0°,0°,0°,0°,0°]T,ω[1]=[0,0,0,0,0]Tω[65]=[0,0,0,0,0]T,θ[129]=[0°,0°,0°,0°,0°]T,ω[129]=[0,0,0,0,0]TP1=(1,-4,0),P2=(1.5,-0.5,0)
机械臂末端由点P1至P2抓取目标后,再返回点P1,释放工件,同时完成机械臂复位归零动作,为进行下一周期工作做好准备。
3.2 不同力矩范围与能耗指标函数J间关系分析
将各关节输出力矩范围限制在Bm=∞,即不限制关节输出力矩范围,经程序迭代计算,得到机械臂工作过程中能耗指标函数值J=2 193.566 6。
以上述Bm=∞的计算结果导入MATLAB中进行仿真,以分解图形式展现机械臂的工作过程,如图4所示,其中大小不同的珠形轨迹线为机械臂第5至第1关节的空间轨迹,最大的珠形轨迹即为由最优化控制所得到的机械臂末端的工作路径。

图4 机械臂的工作仿真分解图 图5 不同力矩范围Bm与能耗指标J值关系
为分析不同输出力矩范围Bm下,机械臂完成同一工作时能耗指标J值的变化情况,将输出力矩范围Bm分别设定在100、90、80、70、65、60、55、54、53、52 N·m,其他初始条件不变,多次进行迭代计算,其结果如图5所示。
为进一步探究不同输出力矩范围Bm下,关节实际输出力矩情况,选取第2、第3关节绘制关节实际的输出力矩变化曲线如图6和图7所示。
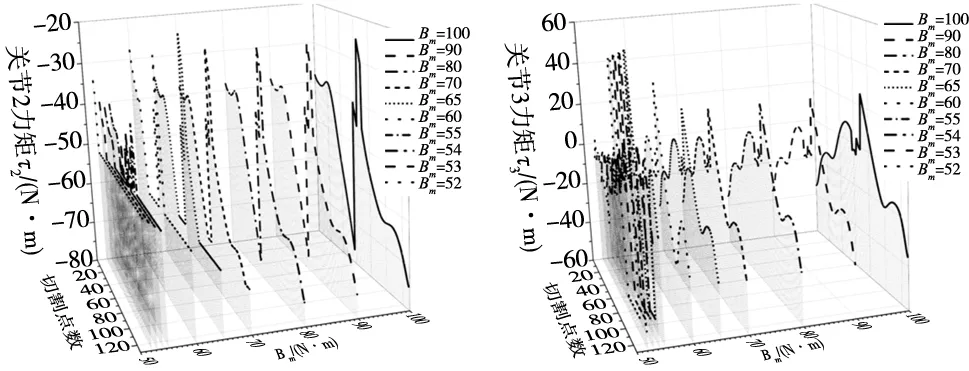
图6 不同力矩范围Bm下关节2实际输出力矩曲线 图7 不同力矩范围Bm下关节3实际输出力矩曲线
由图5~图7可知,随着输出力矩范围Bm的不断减小,关节实际输出力矩被明显地限制在相应范围内,且当Bm减小至65 N·m而继续减小时,能耗指标函数J值急剧增加,故不能为降低制造成本而过分减小电机力矩范围Bm,应将Bm保持在65 N·m左右,既能有效限制力矩范围,降低机械臂的制造成本,又可将能耗指标函数J值降低在较小范围内,进而降低其应用成本。
3.3 不同力矩范围下电机输出力矩频谱分析
为分析输出力矩范围Bm不断减小下,各关节电机实际输出力矩的频谱变化情况,使用快速傅里叶分析(FFT)完成对不同力矩范围下5个关节电机实际输出力矩的频谱分析,其分析结果如图8~图12所示。
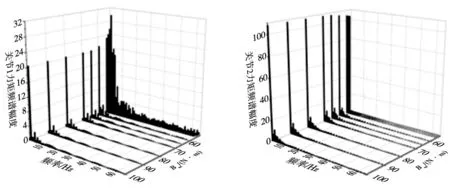
图8 关节1输出力矩τ1频谱 图9 关节2输出力矩τ2频谱
由图可知,随着输出力矩范围Bm不断减小,各关节电机实际输出力矩的频谱逐渐开始变化。以第3关节为例,如图10所示,当力矩范围Bm在65 N·m以上时,电机实际输出力矩的频谱形状基本保持不变,且此时主要集中在较低频域,当力矩范围Bm降低到60、55、54、53、52时,电机实际输出力矩的频谱开始转移到更高的频域,此时机械臂工作易引起电机工作电流的大幅波动,进而导致电机产生振动、冲击,为保证机械臂工作的平稳性,应避免选择力矩范围在65 N·m以下的电机作为关节驱动器。
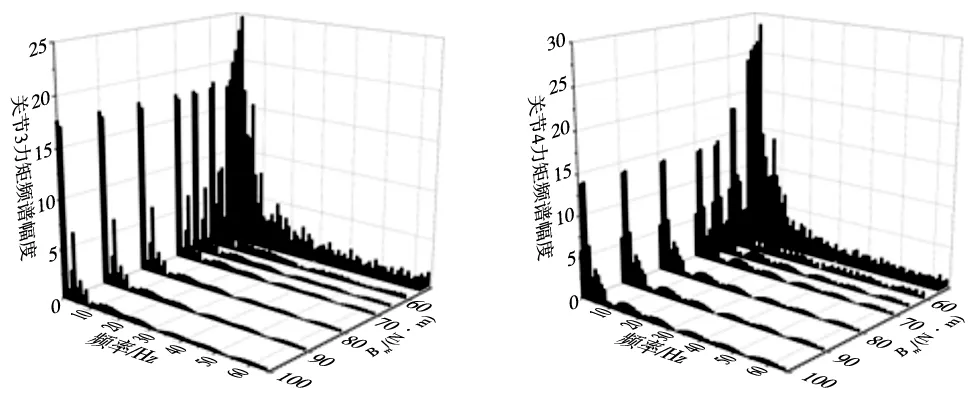
图10 关节3输出力矩τ3频谱 图11 关节4输出力矩τ4频谱
4 总结
针对电机输出力矩范围受限下机械臂的工作能耗问题进行了分析仿真,结论如下:
(1)提出了一种以直接配置非线性规划(DCNLP)处理非线性机械臂系统的方法,解决了电机输出力矩受限下机械臂工作的最优能耗控制问题。
(2)通过仿真得出:当电机输出力矩范围Bm降低到一定值时,机械臂的能耗指标函数J值急剧增加,确定了机械臂完成相同工作下关节电机的临界力矩值,结合各关节输出力矩的频谱图,明确了应将电机的Bm保持在临界力矩值附近,可有效降低机械臂的能耗指标函数J值,减小电机输出力矩范围,抑制电机工作时电流的大幅波动导致的电机振动。

