面向弹性提升的智能配电网远动开关优化配置模型研究

路恒达

（宜兴市供电公司，江苏 宜兴 214200）

0 引 言

现代社会的运转依赖于可靠的电力供应，极端自然灾害和人为攻击给电力安全带来严重威胁。配电网规划和运营中经常会考虑到N-1和N-2故障，极端事件通常会导致N-K的多重故障。建设弹性电网，提高自愈能力和恢复能力，已经成为电力系统发展的先决条件。目前，提高配电网弹性的措施可以分为规划和运营2个方面。规划措施方面包括多层次事故预防、升级变电站、输电线路接地以及弹性资源配置[1]。运营措施方面主要包括使用智能电网等新技术并制定恢复策略，帮助电网实现灾害发生后的有效响应与快速恢复。本文所提远动开关（Remote Controlled Switch，RCS）配置模型属于上述规划措施中的弹性资源配置，通过优化开关位置可以提高分布式配电网恢复负载的能力，并减少极端事件造成的损坏。考虑灾后配电网重建恢复策略，将模型建立为3层鲁棒优化问题，并应用列约束生成（Column-and-Constraint Generation，CCG）算法完成模型求解[2]。此外，提出了一种方法来描述N-K故障对错误传播、链接攻击状态、攻击位置以及关键配置状态的影响，并将其应用在最优规划方案与最严重攻击方式的求解中。

1 问题陈述

配网线路故障后的工作原理和整体RCS恢复过程如图1所示。

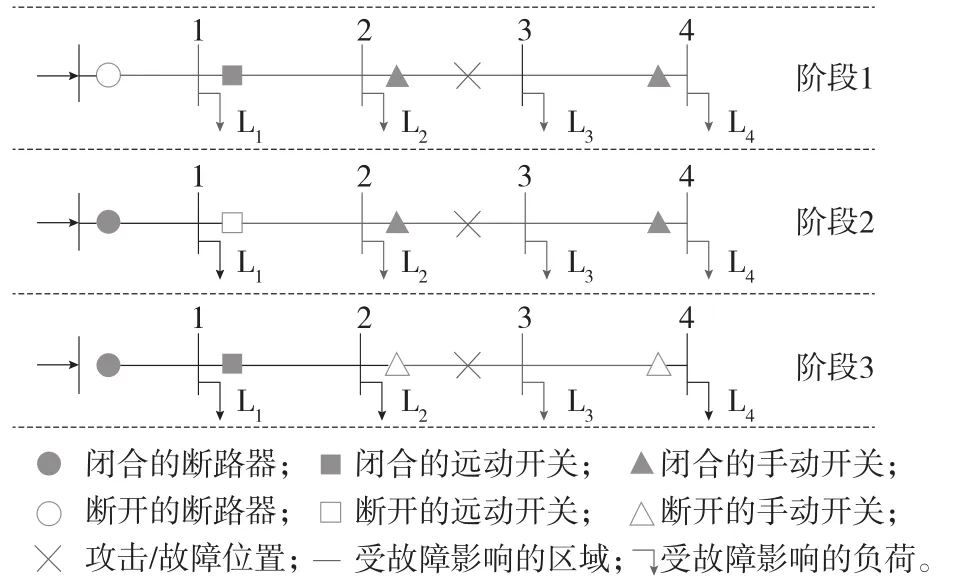
图1 RCS的操作原理和整体恢复过程

阶段1：假设线路2—3发生故障，则所有负载都与开关断开。

阶段2：指挥中心收到错误报告后，通过通信配电网向RCS发送开关操作指令，遥控开关断开并与故障隔离，同时合上开关使L1返回负极。此时，其他负载受缺陷传播的影响，继续处于负载丢失的状态。

阶段3：维修人员使用手动开关复位L2负载，并通过修复缺陷进一步复位其他负载。

RCS配置的结果主要影响第2级负载的恢复（从RCS运行到机控开关的手动控制），本工作仅对这一阶段进行优化。使用RCS进行故障控制，将配电网转换为故障区，并形成分布式能源使能的微电网来恢复负载。结合故障指示器、测量设备、用户反馈等手段有效定位灾后故障，确保RCS和通信系统在故障期间也能可靠运行。

2 模型建立

建立一个强大的3层防御-攻击者-防御（Defender-Attacker-Defender，DAD）优化框架[3]。第1层，规划者规划RCS配置场景；第2层，攻击者寻找最困难的攻击策略；第3层，考虑到可能的恢复措施，寻找最严重攻击策略。与此同时，该攻击策略将返回至第1层作为规划的参考。通过DAD框架，决策制定者可以在系统受到攻击时制定减少危害的计划。为优化目标选择一种RCS配置方案，当使用最大攻击模式和拓扑优化时，最小化灾后切负荷功率。

2.1 配电网潮流运行分布

采用线性化配网潮流模型建立潮流约束，由于正常操作期间的线路网损远小于线路功率，因此配电网损耗项近似为0。此外，正常运行的节点电压均与额定值接近，近似认为线性化配电网潮流模型在弹性配电网的规划与恢复优化中得到了广泛应用。

2.2 配网拓扑约束

2.2.1 径向拓扑的局限性

配电网通常需要运行在辐射状网络结构下，而维持辐射状网络结构的充要条件是闭合线的数量等于拓扑中的节点数与子图数之差、每个线程的连接都完成。在配电网更新过程中，子图可能包括连接变电站的子图、仅由分布式电源供电的子图以及无源孤岛子图。配电网重构过程中形成的子图如图2所示。

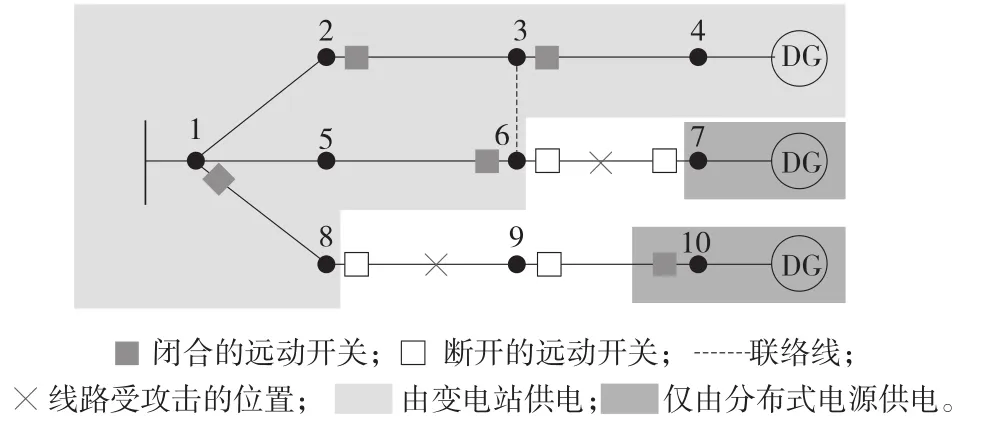
图2 配电网重构过程中形成的子图

在线路6—7和线路8—9受到攻击后，在最近的RCS隔离故障节点7和10处分别形成由分布式电源（Distributed Generator，DG）供电的子图，节点9形成无源孤岛子图，其余节点形成连接变电站的子图，此时联络线为断开状态，以保持辐射状拓扑[4]。

2.2.2 错误传播和线路条件约束

以线路i—j为例，展示了节点j会受到故障传播影响的2种场景，如图3所示。场景1是i—j线段被攻击，节点j未配置RCS；场景2是由于故障，其他线段转移到节点i，节点i—j两侧均未配置RCS。

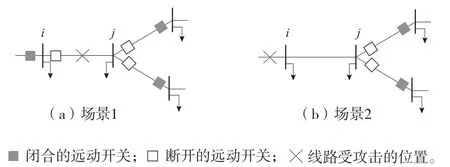
图3 节点j受错误传播影响的场景

3 模型解决方案

CCG算法将初始设计问题分解为更复杂的下层问题，能够解决强大的RCS配置优化问题。每次重复后，下层问题以切负荷功率最大化为目标求解给定规划方案后的最严重攻击方式，并将攻击方式返回到上层问题的确定集中，所得切负荷功率为原问题提供上界。上层问题针对过往所有下层问题所返回攻击方式组成的确定集，通过最小化负载放电功率来选择最优调度方案。由于顶层是原问题的松散问题，因此产生的装机负荷功率提供了原问题的下限[5]。

由于下层问题求解最严重攻击方式时考虑了拓扑重构等恢复措施，引入了离散的线路状态变量，因此能直接对偶为最大化问题求解。下层问题本身仍是一个双层鲁棒问题，即求解一个最严重攻击策略，使其在最优潮流和重构措施下造成的切负荷功率最大。将下层问题进一步分解为下层主问题和下层子问题，其中下层子问题在给定攻击下求解最优拓扑重构方式并将拓扑重构结果返回下层主问题，而下层主问题则针对给定的一系列重构拓扑的集合求解最严重攻击策略。

4 算例研究

本文提供了一个改进的IEEE-37节点系统，其系统拓扑如图4所示。

图4 改进的IEEE-37节点系统

3个容量为500 kVA的DG分别配置在节点709、节点734、节点744。节点701与变电站相连，并将线路连接到断路器。

4.1 RCS数量对系统阻力的影响

求解模型时，预算开关数量CN为3、5、7、9，最大攻击线路数CB分别为3和5，不同规划与攻击预算下的负荷切除功率如表1所示。其中，Cmax为规划开关数量的最大预算。

表1 不同攻击计划和预算下的负载负荷切除功率 单位：kW

开关数量的增加可以减小灾后负荷切除功率，提升系统弹性。当CN达到一定水平，增加开关的数量对提高弹性将没有显著影响。为了进一步确定合理的CN范围，提高规划经济性，设置Cmax=32，将20条候选线路两侧均配置RCS再求解模型。当CN达到9时，已经能够在极大限度上发挥RCS对系统弹性提升的作用。

4.2 未指定组的选择

针对同攻击线路数量求解模型得到的最优配置方案会有所不同，设定过高的确定水平将增加鲁棒优化的保守性，而过低的确定水平下制定的决策难以应对比预期更严重的极端事件打击。定义遗憾值表示针对一种最大攻击线路数CB得到的最优配置方案在施加其他最大数量的攻击时与相应最优配置的表现差异，通过参考同方案的间接比较结果，可以避免做出非常保守或片面的决定。在更高级别的确定性下，CB=2解决方案的分配效率较低。选择CB=3或CB=4可以提供更有效的鲁棒配置方案，以减少遗憾值。

4.3 算法求解效率

在CB=3和CN=5、6、7时，上层主题的最大重复次数KH、低层主题的最大重复次数KL以及模型求解时间T如表2所示。

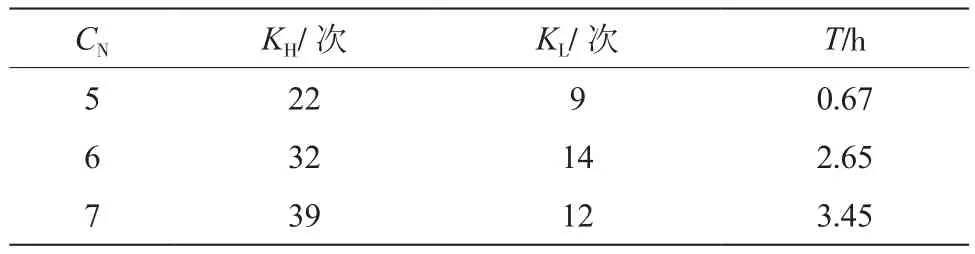
表2 重复次数和求解时间

CCG算法会随着迭代增大问题规模，当迭代次数较多时，上层问题求解时间会大幅增加。由于规划问题对求解时间没有过高要求，因此可以通过离线方式求解。此外，对于大型系统案例，可以将其分解为多个相互连接的子区域，以独立解决规划问题，降低计算复杂度。

5 结 论

通过提出优化RCS配置模型，以提高配电网的弹性和在极端情况下从RCS配置中恢复的能力。基于配电网重构、微网共享等措施，建立反映N—K多重故障传播影响的约束，将线路状态、攻击位置以及开关配置状态相关联，以实现最优规划方案与最严重攻击方式的求解。通过3层DAD框架保障规划决策的鲁棒性，提升系统抵抗严重风险的能力。