风电制氢混合储能系统容量优化配置研究

韩子娇，李 宠，苑 舜，3，董雁楠，马少华

(1．沈阳工业大学电气工程学院，辽宁 沈阳 110870；2．国网辽宁省电力有限公司，辽宁 沈阳 110006；3．国家能源局东北监管局，辽宁 沈阳 110006)

风电作为目前主流的可再生能源之一，装机容量逐年递增，但由于其随机性和反调峰特性，大规模并网对电网产生冲击，影响电网的安全稳定运行[1]。因此各地区存在的弃风问题日益严重，尤其是三北地区，冬季“以热定电”原则使三北地区的弃风问题更加严重，三北地区的弃风电量约占全国弃风电量超过8%的地区，弃风电量为98.2%[2]。在风电基础上增加储能环节是解决弃风问题的有效手段[3]，而氢能作为一种清洁能源受到越来越广泛的关注。我国年产氢量在2300万t左右，约占世界年产氢量的1/3。目前，煤制氢与天然气重整制氢仍然是主流的制氢方式，2种制氢方式所制取的氢气占我国年产氢量的80%。这2种制氢方式会产生大量的碳排放，不利于国家提出的“碳达峰”和“碳中和”目标，因此寻求绿色的制氢途径也迫在眉睫。

利用电网无法消纳的弃风电量电解水来制取氢气能有效解决上述问题。制氢设备和其他储能的容量配置对风-氢系统的运行有较大影响，因此对某一风电场的制氢储能容量进行优化配置一直作为热点备受关注。典型的风-氢发电系统包括制氢、储氢、用氢3个环节[4]，在此基础上，为了降低频繁的功率波动对电解设备制氢效率的影响，文献[5]提出了一种风电/制氢/燃料电池/超级电容器混合系统，有效提高了制氢系统的运行效率。文献[6]在建立了年弃风统计模型的基础上，以经济收益最大为目标，提出了一种利用制氢解决弃风问题的制氢容量配置方法，有效提高了制氢设备的年利用小时数。文献[7]在考虑动态电价基础上，以最小制氢成本为目标函数，提出一种制氢、储电容量配置优化方法。文献[8]构建了外层容量优化配置，内层对电/热综合能源系统进行优化调度的双层规划模型，首先考虑用户侧的电能需求，改变了传统“以热定电”的传统原则。文献[9]建立了风光氢储离网型的综合能源系统，基于混沌粒子群算法对各组成部分进行容量优化配置，又针对该离网型综合能源系统提出能量管理策略。文献[10]以设备安装成本、负荷缺电率和波动率为指标，利用某一天的风速和负荷数据采用改进的遗传算法对离网型风-氢系统进行容量优化配置。然而上述研究没有考虑氢气负荷变化对制氢储能容量配置结果的影响。其次，当风-氢系统中利用弃风电量所制取的氢气不能满足负荷需求、参考系统电能不足时向电网购电的方法，所购氢气制取方式的不同，导致购氢成本和环境成本不同，因此也会对配置结果产生影响。

本文主要针对上述2个问题。首先构建风-氢耦合能源系统，然后采用具有噪声的基于密度的聚类算法(DBSCAN算法)和有序聚类法对年风电-电负荷场景进行聚类，使计算简化，再根据聚类结果得到典型的风电-电负荷场景，以功率平衡和设备运行特性为约束条件，系统年运行成本、设备年化投资成本和维护成本最小为目标函数，对风-氢耦合能源系统的储能单元进行容量优化配置，最后分析系统日均氢负荷变化及购氢渠道不同对容量配置结果的影响。

1 风-氢能源系统

1.1 风-氢能源系统结构

本文构建了一个以风电为主要能量来源且同时含有电负荷与氢气负荷的能源系统，其结构如图1所示。

该风-氢能源系统包括风电场、制氢设备、储氢罐、锂电池、燃料电池和电氢负荷，并与外部电网和氢气网相连接。风电作为清洁能源是系统内部唯一的电源，向系统提供能量。一方面风电向系统中的用电负荷直接供电；另一方面通过电制氢设备制取氢气，所制取的氢气通过储氢罐进行储存，并向系统内部的氢气负荷供氢。当系统中电负荷和氢气负荷无法消纳全部的风电出力时，风电通过锂电池和储氢罐将多余的能量进行储存，并在风电出力不足时补足能量缺额。为了形成一个电-氢-电的能量闭环，使系统具有更大的灵活性，引入了氢燃料电池设备。当风电及锂电池等储能设备同时工作也不能满足系统用能需求时，需要向外部的电网和氢气网中购能。

1.2 系统各设备数学模型

a.风电出力模型

风电实际出力与系统负荷和风速等因素有关，其出力约束为

0≤Pf_e(t)≤Pfeng_max(t)

(1)

式中：Pf_e(t)为t时刻风电的实际出力；Pfeng_max(t)是在t时刻风电的理论出力。

b.制氢设备数学模型

本文中的制氢设备采用目前工业上大规模使用的碱性电解槽，假设对碱性电解槽进行隔热处理，碱性电解槽电解效率不变，其数学模型为

Ppro_h_min≤Ppro_h(t)/ε≤Ppro_h_max

(2)

(3)

式中：ΔPpro_h_min为爬坡约束的下限；ΔPpro_h_max为爬坡约束的上限；ε为碱性电解槽的工作效率；Ppro_h(t)为t时刻碱性电解槽输出氢气功率；Ppro_h_min为碱性电解槽最低制氢功率；Ppro_h_max为碱性电解槽额定制氢功率。碱性电解槽如果运行功率低于10%的额定制氢功率，阳极产生的氧气和阴极产生的氢气有可能发生混和，对系统的安全性产生影响，因此要设置最低的制氢功率。

c.氢燃料电池数学模型

系统通过氢燃料电池在电-氢能源系统中形成能量闭环，可使系统根据实时的需求进行电氢转换，其数学模型为

PFC_e(t)=ηPFC_h(t)

(4)

PFC_h_min≤PFC_h(t)≤PFC_h_max

(5)

ΔPFC_h_min≤PFC_h(t)-PFC_h(t-1)≤ΔPFC_h_max

(6)

式中：PFC_e(t)为t时刻氢燃料电池输出电能功率；PFC_h(t)为t时刻氢燃料电池输入氢气功率；η为氢燃料电池的工作效率；PFC_h_min、PFC_h_max分别为氢燃料电池输入氢气的最小值和最大值；ΔPFC_h_max、ΔPFC_h_min分别为氢燃料电池爬坡约束的上下限。

d.储氢罐数学模型

将碱性电解槽所制取的氢气通过压缩机加压后送入储氢罐进行储存，储氢罐的数学模型为

-Pst_max≤Pst(t)≤Pst_max

(7)

Estr_h(t)=Estr_h(t-1)+Pst(t)dt

(8)

0≤Estr_h(t)≤Estr_h_max

(9)

式中：Pst(t)为t时刻储氢罐出力，正值代表放氢，负值代表储氢；Pst_max为储氢罐出力的最大值；Estr_h(t)为t时刻储氢罐容量；Estr_max为储氢罐额定容量。

e.锂电池数学模型

系统选用锂电池作为储电元件，其运行约束如下，其数学模型为

-Pmax≤Pbatt(t)≤Pmax

(10)

Ebatt(t)=Ebatt(t-1)-Pbatt(t)dt

(11)

0≤Ebatt(t)≤Ebatt_max

(12)

式中：Pbatt(t)为t时刻锂电池功率，正值为放电，负值为充电；Pmax为锂电池最大功率；Ebatt(t)为t时刻锂电池容量；Ebatt_max为锂电池的额定容量。

2 数据处理方法

优化计算时段取为1 h，年运行成本应该对1年8760 h各时段的运行成本进行计算。为了简化计算，对采集的风电-电负荷数据进行处理。为了排除偶然性对优化配置结果的影响，首先利用DBSCAN算法剔除原数据中不合理的数据，然后采用有序聚类对风电-电负荷进行聚类，按照聚类结果计算每个场景各优化时段的平均值，最终将聚类结果的每个场景缩减为1个典型日。

2.1 DBSCAN算法

DBSCAN算法将各数据点分成核心点、边界点和噪声点，将噪声点剔除以减少偶然性或不良数据对计算结果的影响[11]。DBSCAN算法有2个重要参数，半径Eps和最小点数Minpts。聚类过程如图2所示。

图2中设置MinPts值为4，Eps值为3，点A和其他红色点为核心点，在其邻域里包含最少4个点，互相可达，形成了1个聚类，点B和点C不是核心点，但可由A经其他核心点可达，所以属于边界点且与A属于同一聚类。点N是噪声点，点N既不是核心点，也不由其他点可达。将原始的风电-电负荷数据经DBSCAN算法剔除小概率事件，防止偶然性和不良数据对容量配置结果产生影响。

2.2 有序聚类算法

采集的风电-电负荷数据具有很强的季节性而且排列顺序不能被打乱，必须相邻的一组数据才能被分为一类，因此采用有序聚类对采集的风电-电负荷数据进行分割[12]。

某一数据集合G包含{Xi,X2,X3,…,Xu}，首先定义其中位数XG，然后定义这一数据集合的直径D(i,j)，具体表达如式(13)所示。

(13)

(14)

定义分类的损失函数，用b(n,k)表示有n组元素的样品分为k类的某一种分法，其分割点为i1到ik-1，其损失函数为

(15)

当损失函数到达最小，即可得到最优的聚类个数和相应的分割点。

3 系统优化配置

3.1 系统运行功率平衡约束

根据能量守恒定理，本文所构建的风-氢能源系统的电功率和氢气功率要时刻守恒。电功率守恒约束为

PFC_e(t)+Pf_e(t)+Pc_e(t)+Pbatt(t)=Pload_e(t)+Ppro_e(t)

(16)

式中：Pc_e(t)为t时刻向电网购电功率；Ppro_e(t)为t时刻碱性电解槽耗电功率，即输入碱性电解槽的功率。氢气功率守恒为

PFC_h(t)+Pst(t)+Pload_h(t)=Ppro_h(t)+Pc_h(t)

(17)

式中：Pload(t)为t时刻氢气负荷；Pc_h(t)为t时刻系统向外部氢气网的购氢功率。

3.2 目标函数

如果系统中储能单元容量过小，虽然投资成本会降低，但也会导致风能利用率降低，同时会使购电、购氢成本增加从而增加系统的运行成本；储能单元容量过剩，虽然有利于解决弃风问题且减少购能支出，但增加了系统的投资成本，同时设备利用率也会降低[13-14]。因此对储能单元的容量配置要在这多种因素之间进行博弈，以此获得最优的经济性。根据往年风电-负荷按小时采集的数据，以储能设备的投资成本年化、年维护成本和年运行成本最低为目标函数，对风-氢系统的储能单元进行容量配置，其中年运行成本要考虑购能成本、环境成本及弃风成本。目标函数表达式为

F=finv+fmain+fcost

(18)

式中：finv是投资成本年化；fmain为年维护成本；fcost为年运行成本，具体表达式为

(19)

(20)

fcost=fc_E+fcut_e+fenv

(21)

式中：finv,i为第i种储能设备的投资单价；fi为第i种设备的容量；r为这折旧率；Y为设备使用寿命；λ为设备运维系数；fc_E为购能成本，包括购氢成本和购电成本；fcut_e为弃风成本；fenv为环境成本。环境成本设定为购电、购氢产生的碳排放成本，因此购能、弃风和环境成本为

(22)

(23)

(24)

式中：K为有序聚类风电-负荷场景个数；ki为第i个场景所包含的天数；T为调度周期，Ce为电价；Ch为氢气价格；Ccut为单位弃风成本；Cenv为CO2排放成本；σ和α分别为单位购电和购氢产生的碳排放系数。

3.3 优化配置求解

采用粒子群算法对容量优配置问题进行求解，系统采用商业求解器Cplex求解出最优年运行成本，累加上设备投资成本、维护成本作为粒子群算法的适应度函数，求解过程如图3所示。

4 算例分析

4.1 风电-电负荷聚类和数据处理

采集某地区额定容量为1.5 MW的风力发电机理论出力值和周围用电负荷值为样本。数据采集间隔为1 h，将这1 h的风电理论出力和电负荷看作1组二维数据，然后对所采集的1年8760组数据运用DBSCAN算法剔除不合理数据，以防止偶然性对最终容量配置结果的影响，提高配置结果的准确性，结果如图4所示。

将处理后的风电-电负荷数据采用有序聚类，对其进行分割，风电-电负荷的有序聚类结果如图5所示。

由图5可知，风电-电负荷数据被聚类为6类场景，分别提取这6类场景的典型日风电出力及用电负荷数据。以电负荷为例，第5类场景电负荷数据为7100～7820 h的数据，将这720 h的数据储存到一个30×24的矩阵中，该矩阵的每一行即为每日24 h各时段用电负荷值,第5类场景每日用电负荷如图6所示。

由图6可知，每日用电负荷变化趋势基本相同，证明了有序聚类方法的可行性。

对用电负荷矩阵按列求平均值，即可得到第5类场景典型日用电负荷各时段的数值。按照相同的方法处理其他场景电负荷数据和风电数据。聚类所得6个典型日风电出力和用电负荷如图7所示。

由图7可知，各典型日的用电负荷变化趋势明显不同，但却与对应场景的每日出力变化趋势相同，曲线也比较平滑，而风电曲线却呈现出较大的随机性和波动性。

4.2 购氢渠道对储能配置影响分析

系统中风电作为唯一的电源，其所发电能经过碱性电解槽制取氢气满足系统中氢气负荷需求，当风电出力不足时要向外界购氢。在数据处理结果基础上，假设系统的购氢渠道有煤制氢(hydrogen from coal,HFC)和天然气重整制氢(hydrogen from natural gas, HFNG)2种，并假设系统所购电能来自火电机组。考虑不同购氢渠道对系统制氢储能容量配置的影响结果。

采用粒子群算法和Cplex求解器对风-氢能源系统储能容量优化配置进行求解。算例分析所用到的运行参数如表1所示。

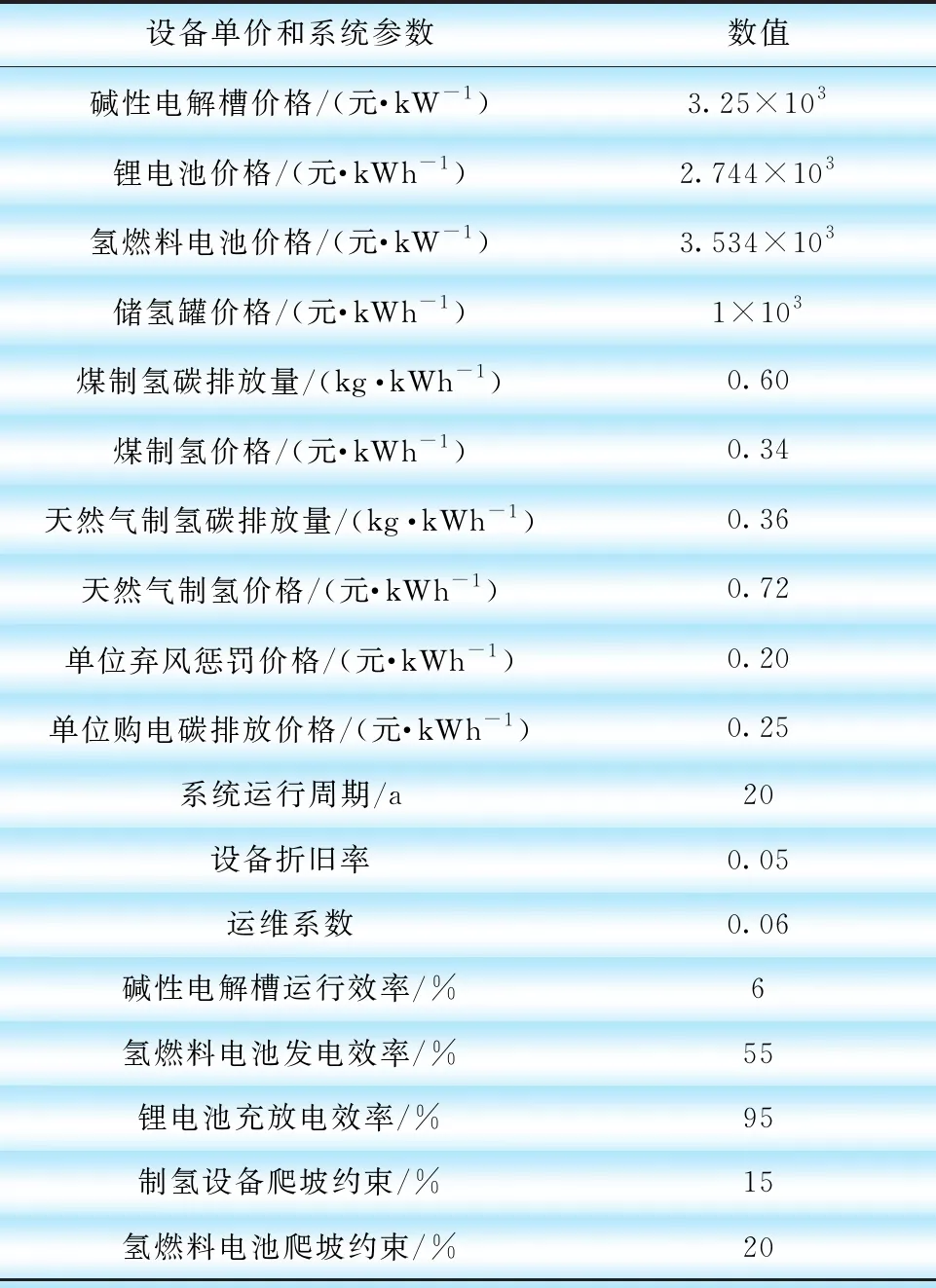
表1 各设备单价及系统运行参数

经Matlab分析，求得不同前提下锂电池、碱性电解槽、燃料电池和储氢罐的最优配置结果[15-17]。如表2所示，煤制氢和天然气重整制氢前提下各设备的最优容量配置结果，日均氢气负荷假设500 kW。

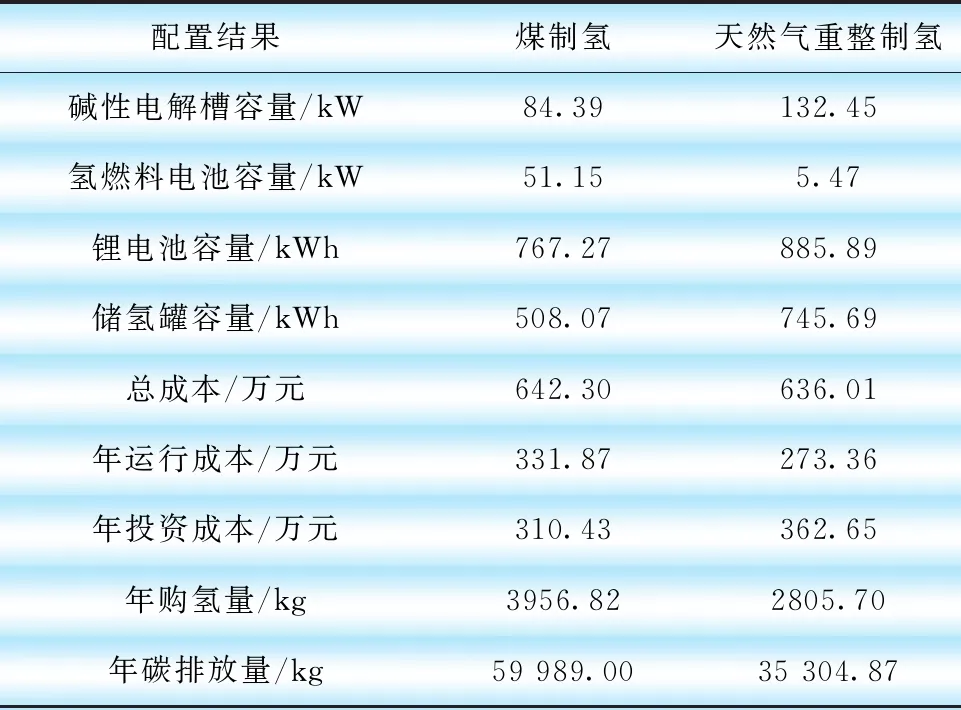
表2 不同购氢渠道下各储能设备容量

天然气重整制氢的氢气价格远高于煤制氢，因此购氢渠道为HFNG时，年购氢量相较于煤制氢下降29.1%，为了满足系统的氢气负荷的要求，HFNG条件下碱性电解槽的最优额定功率为132.45 kW，相较于HFC条件下的84.39 kW增加56%，储氢罐的最优额定容量也增加了46.8%，这就意味着将有更多的电能通过电解槽制氢来满足氢气负荷，因此锂电池的额定容量也有所增加。而氢燃料电池是通过消耗氢气来产生电能，氢气成本的大幅增加及设备效率较低导致其不具有经济性，因此在HFNG条件下，氢燃料电池最优额定功率仅为5.47 kW。

2种购氢途径相比，HFNG条件下储能设备除氢燃料电池外，最优配置容量都比HFC条件下高。HFNG和HFC条件下的储能设备投资成本分别为362.65万元和310.43万元；HFNG和HFC条件下的年运行成本分别为273.36万元和331.87万元，相较于HFC，HFNG的储能设备投资成本上升16.8%，但年运行成本下降17.6%，总成本也有所下降，可见HFNG条件下的经济性略优于HFC。

4.3 日均氢气负荷对储能配置影响分析

假设日均氢气负荷分别为200 kW、300 kW、500 kW，经上述分析，天然气重整制氢经济性略优于煤制氢，所以认为购氢渠道是天然气重整制氢，也假设系统所购电能来自火电机组。求得不同日均氢气负荷下锂电池、碱性电解槽、燃料电池和储氢罐的最优配置结果如表3所示。

表3 不同日均氢气负荷下各储能设备容量

由上述容量配置结果可知，随着日均氢气负荷的增加，系统的运行成本和储能系统的投资成本都有所增加。在风电出力大的时段，无法消纳的电量将分别以电能和氢气的形式分别储存在锂电池和储氢罐中，系统的氢气负荷降低，增加燃料电池的投资尽可能有效利用储存的氢能，同时减少购电以降低系统的运行成本，因此燃料电池的最优容量不同于其他储能设备，其随着氢气负荷的降低而升高。但是，随着氢气负荷的提升，系统的弃风电量明显降低，当日均氢气负荷为500 kW时，弃风电量仅为688.43 kWh，由此也证明，耦合制氢设备可以有效降低系统弃风，从而提高风能利用率。

5 结语

本文构建了风-氢能源系统，并对系统各储能设备进行容量优化配置。通过算例分析得到不同购氢渠道对配置结果的影响，煤制氢的投资成本低于天然气重整制氢，但其运行成本过高，天然气制氢的总成本为636.01万元，煤制氢总成本为642.3万元。从总成本上来看，天然气制氢的经济性比煤制氢略高。同时不难得出，日均氢气负荷的增加会使系统的运行成本和投资成本增加，但可以提高风能的利用率。但本文没对风电的装机容量进行优化，仅仅针对系统的储能环节进行储能的容量优化，这将成为下一步的研究目标。