扎根知识的“来”“用”“走”:从深度学习到深度教学
顾晓峰 (江苏省锡山高级中学 214174)
《普通高中数学课程标准(2017版)》的实施将数学核心素养的发展推向了新的高度,其六大关键能力的获得依赖于对数学知识与技能的深层次学习,因而以深度学习为目标的深度教学成为了当下课堂教学改革的必然选择.
何为深度学习?郑毓信将其与“浅度学习”做对比时指出,浅度学习主要依靠死记硬背与机械模仿,满足于内容的简单积累,最终造成了“知识碎片化”的现象[1].深度学习则有效地避免了学习的肤浅化,重视对知识三个维度的认识:第一,关注怎么来,即知识的来龙去脉、发生过程;第二,关注怎么用,即知识如何纳入到已有认知结构,形成基本的数学能力以解决新情境下的新问题;第三,关注怎么走,即知识之间如何交融与综合,发展到新一层次的认知水平.基于深度学习的特点,深度教学重在引导学生深度参与学习过程并深刻把握学习内容,通过交互式的学习方式,激活原有认知结构,激发内部学习动机,激起思维与情感的体验,有效落实数学核心素养.
1 追根溯源——理解知识的内涵
在传统教学中,教师为争取更多训练时间,对知识概念通常进行粗放地介绍甚至直白告知,致使学生的学与教师的教难以产生共鸣.而深度学习扎根于知识间的联系,注重揭示知识的内涵,让学生感悟知识生成的背景和意义.


图1


图2
2 情境建构——促发知识的应用
基于高中生的认知程度,要使他们在数学学习的过程中获得深度体验,情境的有效建构是必不可少的.正如心理学家克劳德·巴斯蒂安所说,认识的进化并非朝向建立愈来愈抽象的认识,而是朝向把他们放置到背景中[3].因此,在教学中应充分利用学科知识、环境资源与学生的心理特点,建构适宜的情境来深入学习数学.


图3
再比如笔者了解到班级很多男生喜欢看台球比赛,于是设计了如下问题:台球是起源于欧洲的一项高雅室内运动,通过击中目标球或者对方失误而得分.现在台面上有一只白色母球,击打它后要使它碰到蓝色目标球,该怎样控制球杆的方向呢?由于是以真实的体育项目作为问题背景,顿时吸引了学生的“玩劲”,分析击打台球后球是沿着直线运动,于是画出俯视图,将台球分别抽象为圆A、圆B,问题归结为:找到一个方向,使得圆A的圆心在此方向上运动时,两圆有交点.笔者追问:(1)在A运动的过程中两圆一直要有交点吗?(2)什么叫找到一个方向?怎么确定?问题(1)让学生意识到圆A在运动中只要能与圆B有公共点即可,这是存在性问题.问题(2)引导学生想到可以用斜率或倾斜角来刻画方向,故需通过建系对问题进行转化:平面直角坐标系xOy中,圆B:x2+y2=r2,A(a,b),直线l过点A且斜率为k,若l上存在一点P,使得以P为圆心,r为半径的圆和圆B有公共点,求k的取值范围.这是一个解析几何问题,如果对圆B和点A的位置稍加变化,就成为了2012年江苏高考题第12题(PPT展示),学生“恍然大悟”,原来体育问题还能改编成高考题,而高考题的背后竟然还隐藏着“秘密”!欣喜之余,再次把课堂氛围推向高潮.
波利亚认为,良好的组织使得所提供的知识容易用上,这甚至比知识的广泛更为重要.深度学习不刻意加深知识内容本身的难度,而注重对知识内容的综合应用.因此,深度教学首先要求教师自身进行深度学习,善于发现并建构情境,促发学生将已有的知识(包括技能与思想)应用到那些不再有明确数学脚手架的陌生情境中,让他们经历从感性猜测到理性验证,从设计方案到实际测量,从数学运算到结果解释的过程.久而久之,不仅能使学生体验到数学的实用价值,更对实现“三会”的核心目标大有裨益.
3 迁移学习——深化知识的发展
有学者在对国内数学深度学习的研究进行综述后将其特征归纳为四点:深度理解、深度探究、深度体验、深度思维[4].其中深度思维指向学生的高阶思维,包括对知识的自主学习与创新,这要求学生在面对问题(尤其是具有挑战性的问题)时具有敏锐的洞察力,批判性的眼光和发散性的思考,而这方面能力的培养,笔者比较推崇实施迁移学习策略.
例如,在评讲苏锡常镇一模试卷的解析几何题时,笔者与学生展开了以下探究.



类比原问题的解法,学生很快验证了猜想(成为结论1),获得了一定的满足感.笔者继续追问:椭圆是一类特殊的圆锥曲线,大家还有没有更大胆的想法?课堂气氛被点燃,有学生举手提出双曲线和椭圆“差不多”,肯定也有类似结论!但抛物线和它们“长得”不太一样,认为应该没有相关结论.笔者提问,抛物线有焦点、准线、离心率吗?抛物线有切线吗?既然都有,那问题的本质属性有变化吗?此时学生若有所思,觉得抛物线也可以研究.于是笔者将他们分成两大组,一组研究双曲线,一组研究抛物线,任务是提出相关猜想并进行证明,然后上台展示和说明.最终得出两个新命题:

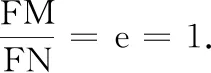
将以上三个结论进一步概括、提炼得到结论4.



图4
结论5设F为椭圆C的一个焦点,n为相应准线,过椭圆C上一点P作椭圆的切线交n于点N,则FP⊥FN.
在课后,通过学习小组的讨论研究,发现结论5实际上提供了一种作椭圆一点处切线的方案(过焦点F作F与椭圆上点P连线的垂线并交相应准线于点N,PN就是椭圆的切线).结论5还可以有其他证法,而且该结论在双曲线与抛物线中依然保留……反思教学过程,种种知识的发现并非是学生(甚至是教师)意料之内的,而是在迁移学习中举一反三,打通个体知识间的关联,逐渐形成新的认知结构.由此可知,在以问题解决为核心任务的教学中,深度学习需要建立在一个良好的母题之上,在教师的协助(组织、提示、补充)下以学生为主体进行迁移学习,自主挖掘知识的内部属性,实现知识的结构重组,在深化知识发展的同时升华数学思维品质.
总而言之,深度教学是促使深度学习的理念跳出纸面,走进课堂,落到实处的深度实践,它承担着培养数学核心素养的重大使命.从这个意义上来说,深度教学应具有其明确特征,它表现在讲清知识的源起生成(回答怎么来),构建情境使得所学知识灵活应用(回答怎么用),创设合适条件进行知识迁移学习(回答怎么走),以使学生在这样的深度学习中获得能力和素养,这甚至可以延伸应用到其他学科的学习与发展中.

