基于对称亮度映射和虚拟多曝光融合的非均匀光照图像增强
黄子蒙,徐望明,2,但 愿
(1.武汉科技大学 信息科学与工程学院,湖北 武汉 430081;2.武汉科技大学 教育部冶金自动化与检测技术工程研究中心,湖北 武汉 430081)
1 引 言
图像增强[1-2]是将待处理图像的细节、边缘、颜色饱和度、对比度等特征进行突出或加强,改善图像质量,方便人眼观察或计算机分析与处理,是进行图像预处理的常见手段。在现实生活中,光照条件是影响成像质量的主要因素之一。图像整体或局部区域过暗或过亮,均不利于人眼视觉观察或机器视觉处理。非均匀光照图像增强技术就是要将原来非均匀光照条件下的图像恢复成正常光照条件下的图像,恢复图像过暗或过亮区域的细节信息,扩大图像中不同物体的特征差异,进而提高这些特征的可辨识度。目前,常用且具有代表性的非均匀光照图像增强方法大致可分为基于Retinex理论的方法、基于图像融合的方法和基于深度学习的方法。基于Ret⁃inex理论的方法将输入图像分解为两幅子图[3],即带有图像细节信息的反射分量和决定图像动态范围的光照分量。如NPE(Naturalness Pre⁃served Enhancement)[4]方法使用滤波器将图像分解为反射分量和光照分量,并使用对数变换进行亮度分量的增强,但增强后的图像常常会存在伪影的问题;SRIE(Simultaneous Reflectance and Illumination Estimation)[5]方法则使用一种加权变分模型来同时估计输入图像的反射分量和光照分量,虽弥补了在对数域上过于放大暗部区域的问题,但也导致最终非均匀光照图像增强的效果不明显。在基于图像融合的方法中,一项十分困难的工作便是如何基于单张输入图像获得同一场景的不同曝光度下的图像。为此,Ying等人[6-7]提出了基于相机响应模型的方法,通过参数优化虚拟生成最优曝光比下的图像,并与原图像进行加权融合,然而该方法没有处理图像的过曝区域,图像亮区细节会失真。文献[8]根据该相机响应模型提出了一种增强非均匀光照图像的改进算法,对图像亮区也进行了增强处理,但所用亮度映射函数没有归一化,映射结果会存在欠曝或过曝像素,导致部分细节信息的丢失。基于深度学习的方法[9]的性能在一定程度上取决于数据集大小,数据集越大则训练所得神经网络模型泛化能力越强。随着数据集的增长,神经网络模型不仅需要训练更多参数,而且训练数据量也会增加,因此需要高性能计算机用于训练,而采用较小的数据集进行训练则容易出现模型过拟合现象。
为了克服以上方法的不足,针对非均匀光照增强任务,本文提出一种基于对称亮度映射和虚拟多曝光融合的图像增强方法,不依赖于图像数据集,借助相机响应模型及图像信息熵和平均梯度最大化原则估计最优曝光比,并设计对称的亮度映射函数对单张输入图像进行增强曝光和减弱曝光处理,虚拟生成一个具有不同曝光比的图像序列,最后通过带细节提升的多曝光融合方法重构得到一幅动态范围高、对比度强、细节清晰、可视化质量好的图像。
2 相机响应模型
图像的成像过程可用相机响应模型来解释,相机响应函数是描述相机响应模型的具体方式之一。设函数f为相机响应函数,它建立了相机的曝光量E和图像亮度值P之间的非线性映射关系[10]:

设P和P′分别是在同一场景下不同曝光量E和E′拍摄的图像,且E′=kE,其中k为曝光比,则:
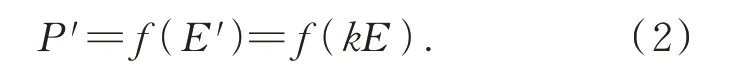
再设函数g为亮度映射函数(Brightness Map⁃ping Function,BMF),用于建立同一场景下不同曝光的图像之间的亮度非线性映射关系[11],则:
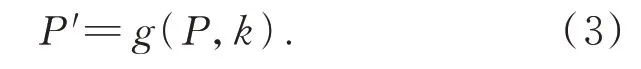
因此,CRF与BMF两函数之间的转换关系可表示为:
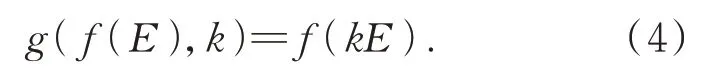
可见,BMF也可作为相机响应模型的一种具体表示形式,目前已有多种方法用于估计BMF。虽然真实场景下图像的曝光量难以得到,但当BMF已知时,利用式(3)就可以通过对原始图像P设置不同的曝光比k来生成不同的图像P′,等同于起到改变图像像素曝光量的效果。将这些具有不同曝光比的生成图像看做一个虚拟的曝光序列,就可以使用图像多曝光融合方法实现对非均匀光照图像增强的目的。
显然,可以直接设置多个不同的曝光比生成一系列图像,但考虑计算效率,一般希望使用尽可能少的虚拟曝光图像,这就需要选用适当的图像质量评价指标作为度量确定最优的曝光比。文献[6-7]及文献[8]均采用图像信息熵这一单一质量评价指标来优化曝光比,依据增强后图像较暗或较亮像素的信息熵大小来确定最优曝光比。这种方法存在一定的局限性,因为信息熵不能反映图像的结构化信息,尤其在非均匀光照条件下图像过暗区或过亮区的局部结构化信息可能丢失。因此,为了实现更好的增强效果,本文在信息熵的基础上加入了平均梯度评价指标来共同优化曝光比,即产生虚拟曝光图像的最优曝光比由增强后图像的信息熵和平均梯度大小共同决定。另外,上述方法所用亮度映射函数没有归一化,虚拟曝光结果图像会存在欠曝或过曝像素,从而导致部分图像细节信息的丢失,且文献[8]要分别对暗区和亮区像素估计不同的最优曝光比,计算比较繁琐,因此,本文进一步改进了亮度映射函数设计方法,提出使用对称亮度映射函数,只需一次估计最优曝光比即可实现对非均匀光照图像进行虚拟增强曝光和减弱曝光,且保持与原图像亮度顺序的一致性,不会出现欠曝或过曝现象。最后,为凸显图像细节,再采用带细节提升的多曝光融合方法重构图像即可实现非均匀光照图像增强效果。
3 非均匀光照图像增强方法
3.1 方法流程
本文提出的基于对称亮度映射和虚拟多曝光融合的非均匀光照图像增强方法的流程图如图1所示。
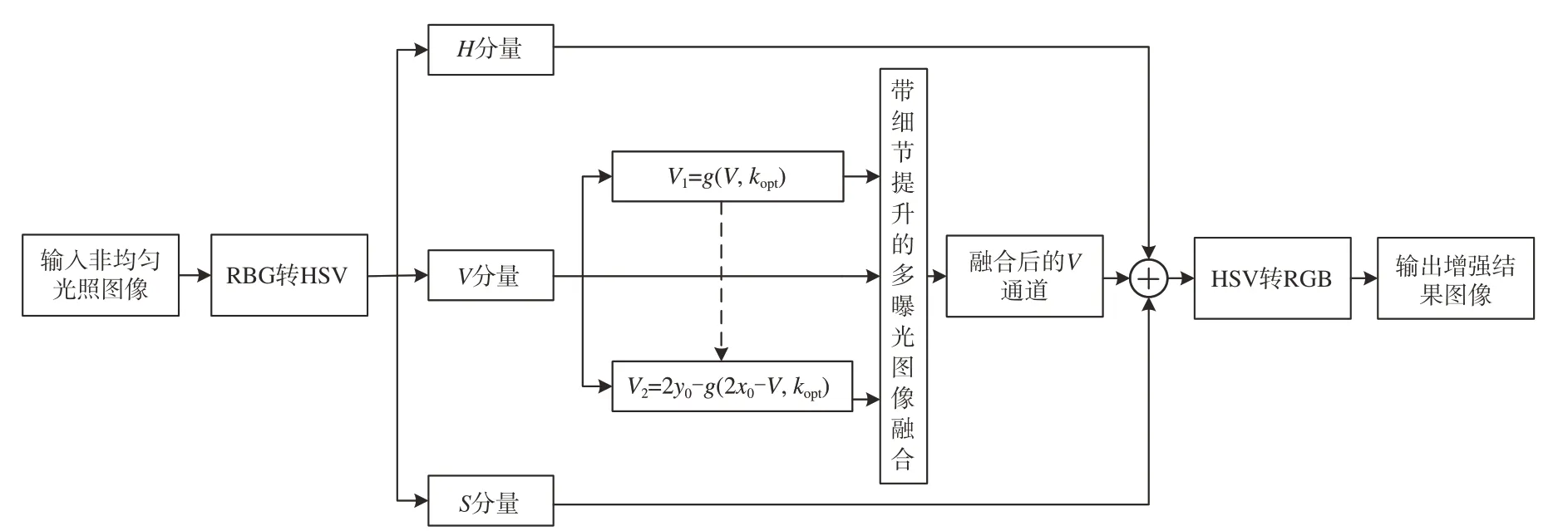
图1 本文方法流程图Fig.1 Flow chart of the proposed method
首先,为了更好地保持图像的颜色信息,将输入的单张非均匀光照彩色图像由RGB颜色空间转换到HSV颜色空间,分离出图像的色调分量图像H、亮度分量图像V和饱和度分量图像S;然后,仅针对亮度分量图像V进行处理,依据信息熵与平均梯度最大化原则来估计最佳曝光比kopt,代入所设计的亮度映射函数g中,对亮度分量图像V进行增强曝光处理,得到增强曝光的图像V1=g(V,kopt),同时利用函数g关于点(x0,y0)对称的亮度响应函数进一步对亮度分量图像V进行减弱曝光处理,得到减弱曝光的图像V2=2y0-g(2x0-V,kopt);接着,为凸显图像细节信息,使用带细节提升的多曝光融合方法,对由图像V、增强曝光图像V1和减弱曝光图像V2组成的虚拟曝光序列进行融合,重构出增强后的亮度分量图像V;最后,将增强后的亮度分量图像V和保持不变的色调分量图像H、饱和度分量图像S从HSV颜色空间转换回RGB颜色空间,得到最终的图像增强结果。
3.2 基于图像信息熵和平均梯度的最佳曝光比估计
图像信息熵[12]和平均梯度[13]是衡量图像质量的两个常用无参考指标。
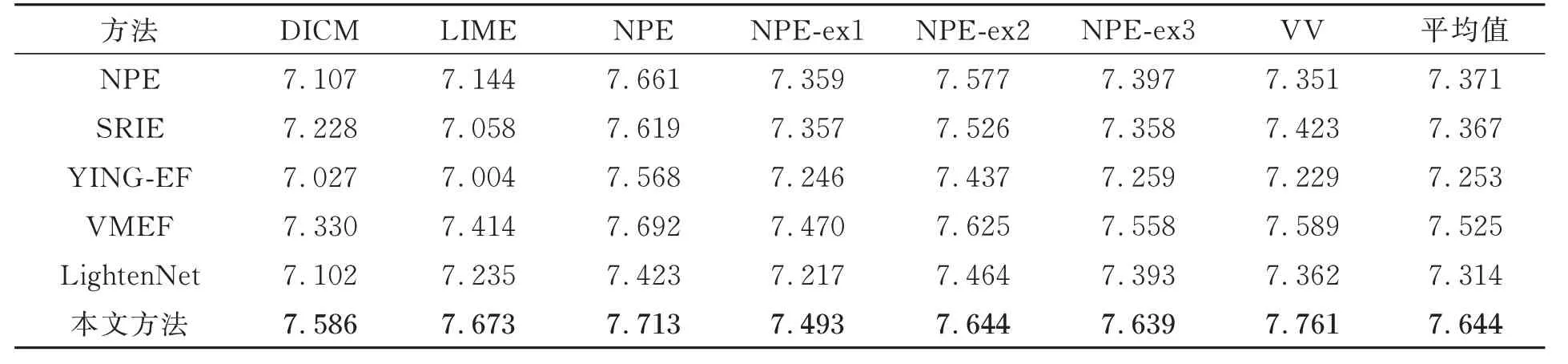
图像信息熵一般用来度量图像信息量,其值越大说明图像中包含的信息越多,计算公式如式(5)所示:

式中J为灰度级总数,pi表示图像I中某处灰度出现的概率。
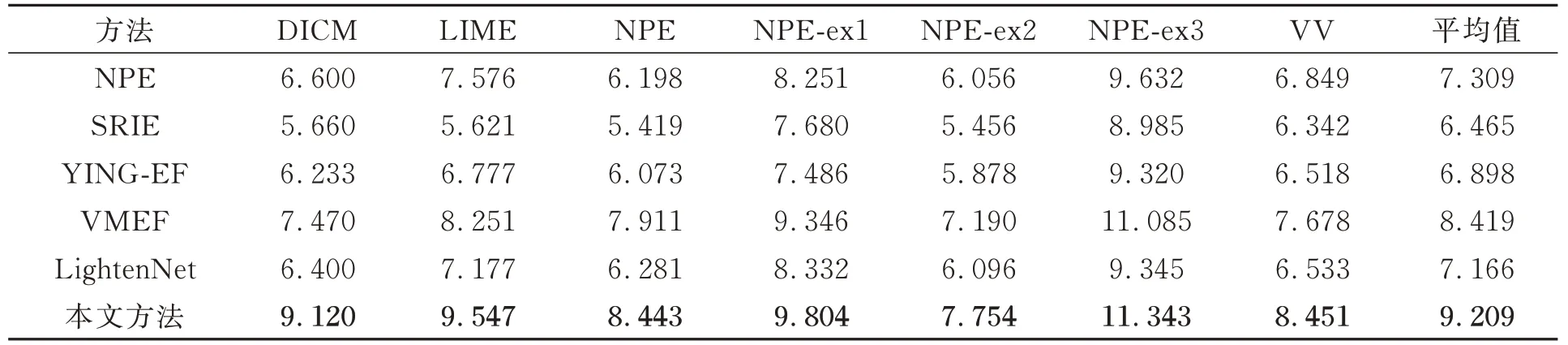
图像的平均梯度代表了图像微小细节反差变化的速率,可以用来表示图像的清晰度,其值越大说明图像的结构化信息越多,图像越清晰,计算公式如式(6)所示:
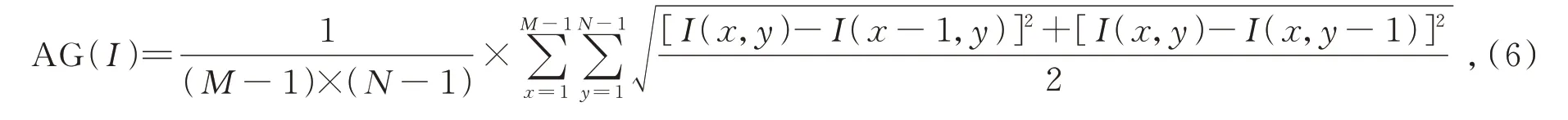
式中M×N为图像大小,I(x,y)为图像I在像素(x,y)处的灰度值。
对于非均匀光照图像,为了实现更好的增强效果,一般先只针对曝光不足或曝光过高的像素集合来估计最优曝光比,再利用此最优曝光比作用于图像中所有像素实现虚拟曝光增强或虚拟曝光减弱效果。
本文方法在估计最优曝光比时,使用图像信息熵和平均梯度最大化原则:使经亮度映射函数作用后的虚拟曝光图像中对应原始图像中曝光不足或曝光过高的像素集合所能蕴含的信息量和清晰度达到最优。该优化问题可以表示为:

其中,Q为原始输入图像中曝光不足或曝光过高像素灰度值集合,g为图像灰度映射函数。
获得仅包含曝光不足的像素灰度值集合Q1和仅包含曝光过高的像素灰度值集合Q2的判定方法为:
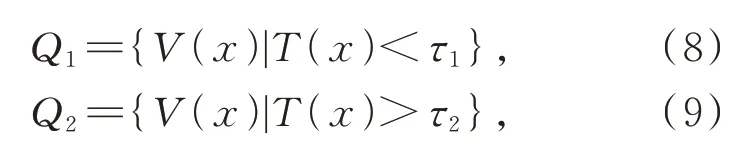
式中T(x)为图像V的光照分量图,估计T(x)的方法可以参见文献[6-7];τ1和τ2分别为区分曝光不足和曝光过高像素的灰度阈值,本文中图像灰度归一化后取τ1=0.5,τ2=0.5。式(7)中,Q=Q1时,要满足k>1;而Q=Q2时,要满足k<1。
3.3 对称亮度映射函数
由于非均匀光照图像存在曝光不足和曝光过度两种情形,如果使用统一的曝光比直接对非均匀光照图像进行曝光补偿等增强处理,无法使所有像素曝光良好。因此需要选择合适的亮度映射函数对曝光不足区域做增强曝光处理,生成增强曝光图像,提高原图像中的局部亮度偏低像素的灰度值;对亮度过高区域做减弱曝光处理,生成减弱曝光图像,降低原图像中的局部亮度偏高像素的灰度值。
以v表示某一亮度值,k表示曝光比参数,亮度映射函数g(v,k)的设计一般应满足3个条件:
(1)为防止映射后图像相邻像素之间的亮度值差异消失,函数必须是严格单调的,即对任意v2>v1,须满足g(v2,k)>g(v1,k)。
(2)为防止映射后像素亮度值截断导致信息丢失,要保证归一化输入图像的每个像素亮度值仍被映射至归一化区间[0,1],即g(0,k)=0,且g(1,k)=1。
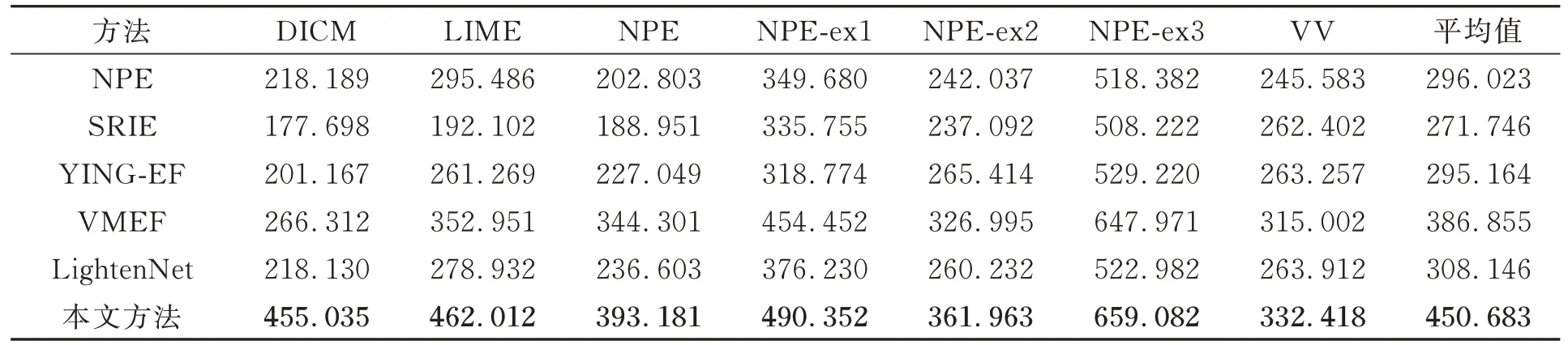
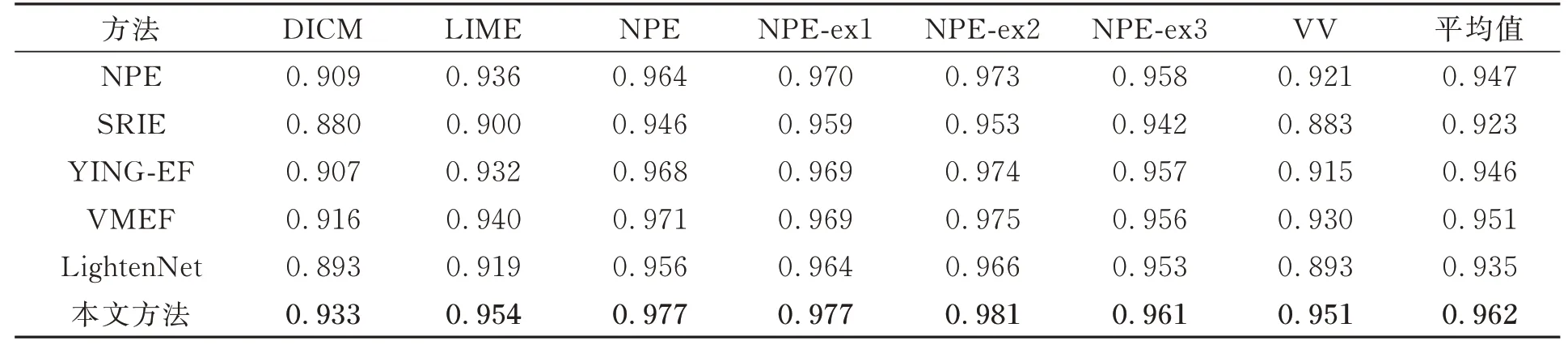
(3)曝光比k控制着曝光效果。当k=1时,g(v,1)=v,即曝光不变;对于任意(0,1)之间取值的像素v,当k>1时,g(v,k)>g(v,1)=v,即增强曝光;当k<1时,g(v,k) 当生成增强曝光图像时,文献[4-6]中方法所采用的亮度映射函数为: 其中a=-0.329 3,b=1.125 8。实验结果表明,该函数取得了较好效果,但它不满足上述条件(2),会在输入图像亮度值较大时产生截断而丢失亮区的信息。 为了利用该函数的效果优势并弥补其不足,本文以分段的形式定义一种改进的亮度映射函数: 为保证函数连续,须满足g1(θ,k)=g2(θ,k)=ε,ε为分段点自变量θ所对应的映射值。反过来通过指定ε也可求出θ,本文取ε=0.9以得到较好的暗区对比度提升效果。 这里g2(V,k)的主要作用就是防止图像亮度值超过1而被截断,起到保留原始图像亮区灰度信息的效果,可选函数很多,为便于计算,一种简单的函数形式是取经过点(θ,ε)与(1,1)的直线,即: 当ε=0.9时,改进前后的亮度映射函数曲线如图2所示。 由图2可知,该函数能较好地拉升图像暗区像素的亮度值,增强图像暗区像素的对比度。 图2 改进前后的亮度映射函数曲线对比Fig.2 Comparison of the original and improved BMF curves 根据函数点对称性质可知,当想要较好地拉升图像亮区像素的亮度值,增强图像亮区像素的对比度时,可直接选择使用该亮度映射函数关于点(x0,y0)对称的函数生成减弱曝光图像:V2=2y0-g(2x0-V,kopt),这 里x0=0.5,y0=0.5,从而无需重新估计新的最优曝光比和设计新的亮度映射函数。 当ε=0.9时,用于增强曝光的亮度映射函数与用于减弱曝光的亮度映射函数所组成的对称双曲线如图3所示。可见,增强曝光的BMF曲线拉伸了低光区域的亮度对比度,而保持着高光区域的亮度一致性;相反,减弱曝光的BMF曲线拉伸了高光区域的亮度对比度,而保持低光区域的亮度一致性。两条曲线同时作用于原图像,即可虚拟生成对应的增强曝光图像和减弱曝光图像,加上原始输入图像,就可看做是一个由3幅不同曝光图像组成的信息互补的虚拟多曝光序列。 图3 对称亮度映射函数曲线Fig.3 Symmetric BMF curves 对非均匀光照图像,在增强图像对比度的同时,还希望尽可能地凸显图像细节。因此,本文最终图像增强结果采用带细节提升的多曝光融合方法[6]将图像V以及虚拟曝光生成的两幅图像V1和V2进行信息融合而得到。 具体而言,首先要将曝光序列中的任一图像分解为不同尺度下的基础层和细节层,这里用3个不同尺度的高斯卷积核分别对待处理图像进行滤波,即: 式中Vn为曝光序列中第n幅图像,Bn,i(i=1,2,3)为第n幅曝光图像在不同尺度下的基础层,Dn,i(i=1,2,3)为第n幅曝光图像在不同尺度下的细节层,Gi(i=1,2,3)为标准差为σ1=1,σ2=2和σ3=4的高斯核,∗表示卷积运算。 然后,取最小尺度的高斯核卷积得到的基础层作为后续融合的基础层图像,即第n幅曝光图像对应的基础层Bn=Bn,1,细节层图像则由上述3种尺度下的细节层加权重构得到: 式中w1、w2、w3为权重系数,sgn为符号函数。 接着,采用将像素显著性和空间一致性相结合的方法计算Bn和Dn的权重图,其步骤如下: (1)利用3×3的拉普拉斯滤波器L与每幅图像Vn进行卷积,得到高通图像Hn: 用Hn绝对值的局部高斯平滑处理结果构建显著性图像Sn: 式 中Rrg,σg是 大 小 为(2rg+1)×(2rg+1)、标 准 差为σg的高斯低通滤波器,其中rg=5,σg=5。 (2)通过比较不同的Sn中相同位置像素的显著性数值确定初始的权重图中对应位置的权重值为: 式中N为图像的数量,为第n幅图像在第k个像素处的显著性数值。 (3)利用引导滤波能保持像素空间一致性的优点来改善初始权重图Pn,将Pn作为引导滤波的输入图像,将与Pn对应的图像Vn作为引导图像,即: 然后,将N个基础层权重图和N个细节层权重图在相同像素位置分别做和为1的归一化处理,再通过线性加权的方法分别进行融合,即: 最后,将融合后的基础层与融合后的细节层Dˉ相加,得到最终的重构图像I: 为了验证文本方法对非均匀光照图像增强的可行性与有效性,选取DICM[14]、LIME-data[15]、NPE-data[4]及其扩展集NPE-ex1、NPE-ex2、NPEex3以及VV[16]等7个公开数据集进行了对比实验,实验后进行了图像质量的主客观评价。对比方法包括经典的方法NPE[4]和SRIE[5]、基 于 图像融合的方法YING-EF(Exposure Fusion)[7]和VMEF(Virtual Multi-Exposure Fusion)[8]、基于深度学习的方法LightenNet[17],其中对比方法的参数设置保持原论文设置不变。 为了客观评价本文方法,采用图像信息熵、平均梯度、图像对比度、颜色一致性作为客观指标来衡量方法性能。图像对比度代表了图像亮区暗区拉伸的对比程度,其值越大说明图像的灰度反差越大,图像的动态范围越高,其计算公式如式(21)所示: 其中,δ(i,j)=|i-j|,即相邻像素间灰度 差;Pδ(i,j)为相邻像素间的灰度差为δ的像素分布概率。将图像中每个像素点的R、G、B值看作3维空间的1个颜色向量,则颜色一致性度量为计算原图像与增强图像所有对应像素点的颜色向量夹角余弦值[18]的平均值,其值越大表明图像增强后的颜色与原图像差异越小,其计算公式如式(22)所示: 其中,I和E分别为原图像和增强图像,θp为像素点P处的颜色向量夹角,n为像素点总数。 客观评价指标的实验结果如表1~4所示。表中每个数据集对应的结果是该数据集上所有图像相应评价指标的平均值,最后也记录了所有数据集上图像的整体平均值。 表1 不同方法在各数据集上的图像信息熵Tab.1 Image information entropy of different methods on each dataset 结果表明,NPE、SRIE、YING-EF和Lighten⁃Net方法的增强效果比较接近,均处于较低水平;VMEF方法略高于NPE、SRIE、YING-EF和Light⁃enNet方法;而本文方法在图像信息熵、平均梯度、图像对比度、颜色一致性等客观评价指标上均表现为最高,在7个公开数据集上相应评价指标的整体平均值分别达到了7.644,9.209,450.683,0.962,与对比方法相比均有显著提升。 表2 不同方法在各数据集上的平均梯度Tab.2 Average gradients of different methods on each dataset 表3 不同方法在各数据集上的图像对比度Tab.3 Image contrast of different methods on each dataset 表4 不同方法在各数据集上的颜色一致性Tab.4 Color consistency of different methods on each dataset 为了能够真实地反映本文方法对非均匀光照图像增强的直观效果,从实验结果中挑选了两幅具有代表性的图像及其细节放大图(红色方框标出),如图4、图5和图6所示。可以看出,SRIE和YINGEF方法对于图像的增强并不明显,增强后图像对比度仍偏低,不利于人眼分辨图像信息;图4中汽车和街道部分、图5中树和沙滩部分以及图6中洞壁和人脸部分,由NPE、VMEF和LightenNet方法处理的图像亮度较暗;而本文方法增强的图像不仅对比度较高,而且细节清晰、色彩层次感丰富,相较于其他算法的可视化效果有了明显提升。 图4 非均匀光照图像增强结果对比(示例1)Fig.4 Comparison of image enhancement results for non-uniform illumination image(Example 1) 图5 非均匀光照图像增强结果对比(示例2)Fig.5 Comparison of image enhancement results for non-uniform illumination image(Example 2) 图6 非均匀光照图像增强结果对比(示例3)Fig.6 Comparison of image enhancement results for non-uniform illumination image(Example 3) 为解决非均匀光照图像出现的各种问题,如对比度低、细节不清晰、可视化效果差等,本文提出了一种基于对称亮度映射和虚拟多曝光融合的非均匀光照图像增强方法,通过两条对称的亮度映射函数曲线分别对非均匀光照图像的欠曝光区域做增强曝光处理,对过曝光区域做减弱曝光处理,然后使用带细节提升的多曝光融合方法对原图像、减弱曝光图像和增强曝光图像组成的曝光序列进行融合得到最终的增强图像。在7个公共数据集上的实验表明,本文方法取得的图像信息熵、平均梯度、图像对比度、颜色一致性4种客观评价指标均值分别为7.644,9.209,450.683,0.962,均优于对比方法,获得了动态范围高、对比度强、细节清晰和可视化效果好的增强结果。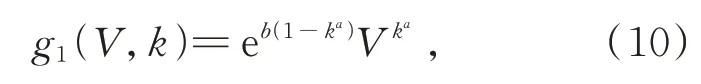
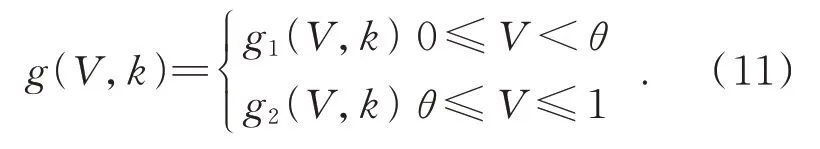

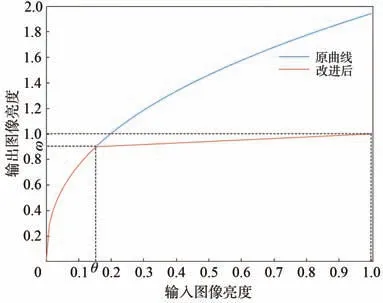
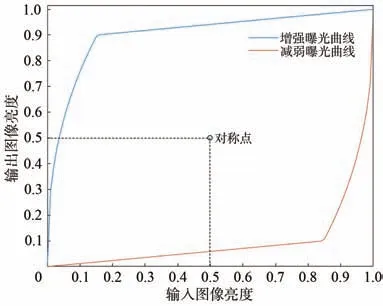
3.4 带细节提升的虚拟多曝光融合
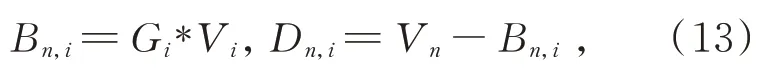
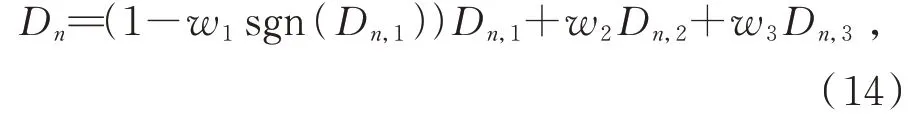


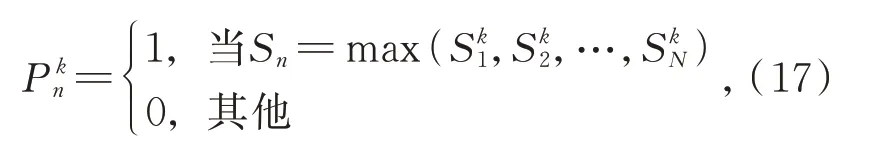
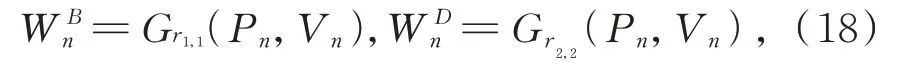
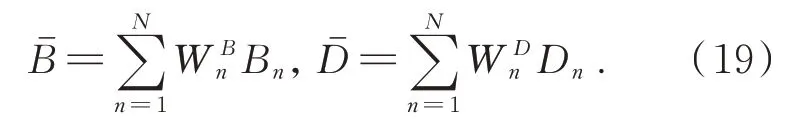

4 实验结果及分析
4.1 实验结果客观评价

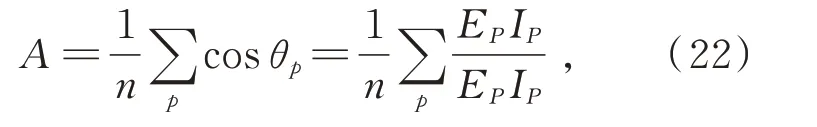
4.2 实验结果主观评价



5 结 论

