精准诊断破抽象 有效拓展提素养
潘光勇 (浙江省青田县中学 323900)
在网络信息发达的今天,各地的高考模拟试题如雨后春笋般冒出来,“好题”不断,给一线的数学教师提供了很多可以拓展的知识素材,也为各种“秒杀技”提供了肥沃的土壤.利用某些特殊的二级结论(即一些拓展知识)可以在解题过程中实现“秒杀”,在追求“秒杀”的过程中教师总是主动(或被动地)进行各种“秒杀”知识的拓展.这些拓展知识除了让学生听得“云里雾里”、似懂非懂外,也极大地影响着教师对知识拓展方向和拓展深度的判断,严重影响高三数学复习课的教学质量.同时也增加了学生的学习负担,学生总觉得有学不完的数学知识;打击了学生学好数学的自信心,对学生基础知识和基本技能的落实以及数学素养的培养产生不可估量的负面影响,实在是得不偿失.对于一线高三数学教师来说,对某些重要的学科主干知识进行拓展延伸是一件正常的事,但在复习教学时要拓展什么内容、拓展到什么程度、按什么逻辑顺序进行拓展,这些问题却让很多教师纠结、迷茫,很多教师只是“随卷而动”“随题拓展”,盲目跟风.
本文以2020年11月浙江省衢州、丽水、湖州三地市教学质量检测试卷第21题解析几何题为例,从案例展现、拓展有理,真题研磨、拓展有向,反思教学、拓展有法三个方面出发,谈谈如何在高三数学教学时进行知识的有效拓展.
1 案例展现,拓展有理
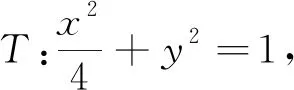
(1)当点G在椭圆T上时,求GF的值;
(2)如图1,过点G的直线l1与椭圆T交于P,Q两点,与抛物线M交于A,B两点,且G是线段PQ的中点,过点F的直线l2交抛物线M于C,D两点.若AC∥BD,求l2的斜率k的取值范围.
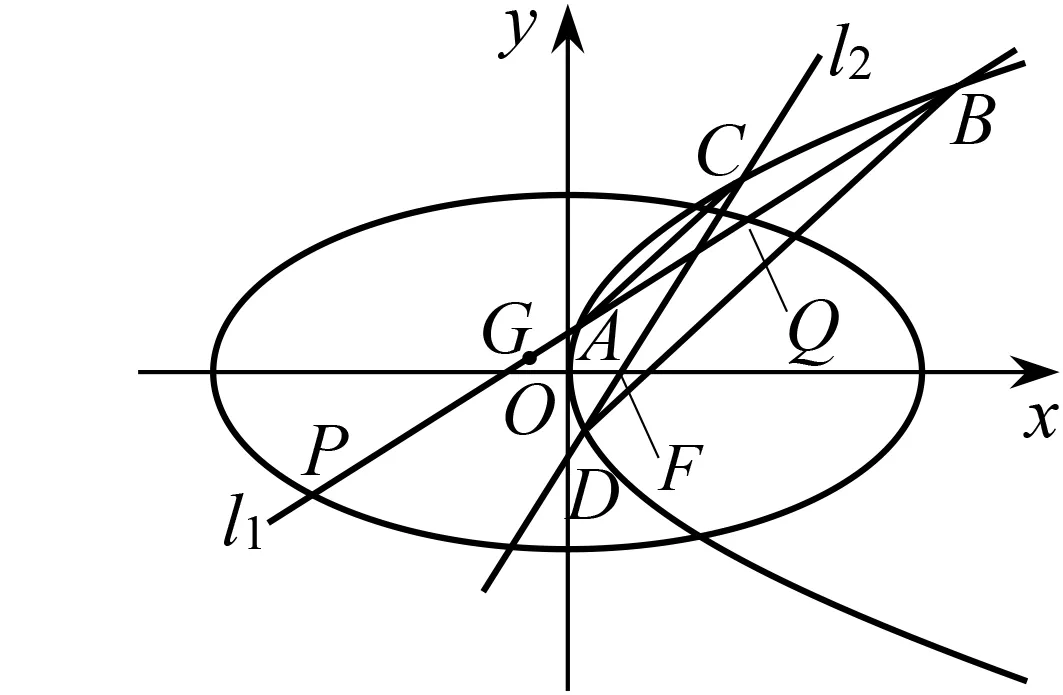
图1
1.1 数据查因,精准诊断
笔者对学生答题情况和后台数据进行分析,发现多数学生只能完成第(1)小题的解答,对第(2)小题无从下手或者解题思维混乱,平均得分为5.86分,解析几何相关的数学素养欠缺明显.通过对学生答卷重新进行面批以及对答题数据进行分析,学生的错误原因初步诊断如下.
诊断1 图形复杂直线多,起步艰难缺方法.学生畏难情绪严重,静不下心来分析试题中各几何元素间的关系.
诊断2 在已知中点的情况下,不会求弦l1的斜率,说明学生对重要知识的掌握不娴熟,数学素养有待提高.
诊断3 对试题中的直线与椭圆、直线与抛物线的关系不清晰,没能从直线AC与直线BD平行这一条件找到解题的化简目标.
从整个改卷情况看,多数学生对解析几何涉及的基础知识、基本方法、基本技能的掌握还不到位,没有明确的解题目标,缺少积极的思维心态和数学素养.
1.2 理清关系,破解难点
本例中涉及的图形有椭圆、双曲线、过点G的直线、过点F的直线.点G是椭圆弦PQ的中点,由点差法可以求出弦PQ所在直线l1的斜率,故可以求出l1的方程.由AC∥BD知,两直线的斜率相等,必然涉及到A,B,C,D四个点的坐标,必须要让直线l1,l2分别与抛物线方程联立,利用韦达定理找出坐标间的关系,从而实现顺利求解.
1.3 再现基础,顺势拓展
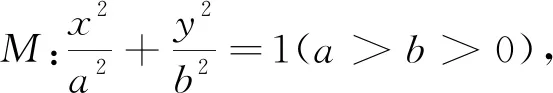
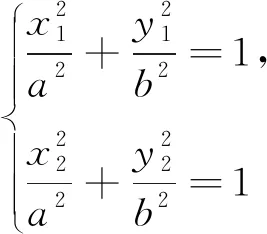
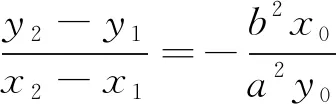
1.4 灵活应用,简化运算
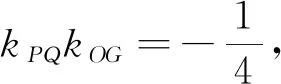
从本例的解析可以看出,对椭圆的中点弦问题进行知识拓展显得非常必要.抓住问题的结构特征,运用已掌握的拓展知识,简化直线l1方程的求解,对本题的顺利求解起到非常重要的作用.
2 真题研磨,拓展有向
“磨刀不误砍柴功”,在高三的数学复习教学中明确复习方向,才能让知识拓展“有的放矢”.然而,高中数学知识点中可以拓展的知识点多,仅圆锥曲线中可以拓展的“二级结论”就多达上百条,如此多的“二级结论”全部拓展一遍,不仅耗时耗力,学生也掌握不了.对于如何把握知识拓展内容和拓展方向,教师可以从以下几个方面进行操作.
2.1 重做真题,拓展有向
比如,引例中出现的拓展知识点:椭圆中的“垂径定理”,在高三的复习教学中,有没有必要对此进行拓展、拓展到什么程度,这样的拓展能否有助于学生解决相关试题?我们可以通过研磨历年的浙江高考数学真题,从中寻找答案.

图2


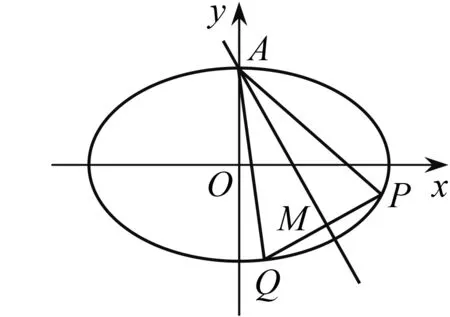
图3

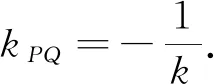
从近五年浙江高考卷的解析几何题中我们可以发现,椭圆中的“垂径定理”这一拓展知识的运用还是比较常见的.对于涉及椭圆中点弦的相关问题,学生容易运用这一结论简化运算、理清解题思路,寻找试题的解决方向和目标,避免繁杂的运算.像这种在高考试题中经常出现的知识,我们进行重点知识拓展是非常必要的,而且是必须的.这种知识拓展不仅不会增加学生的负担,还能优化运算,何乐而不为?
2.2 宽度拓展,发展素养
椭圆中具有这样精美的结论,那么双曲线、抛物线中否也具有相似的结论呢?
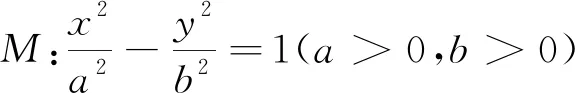
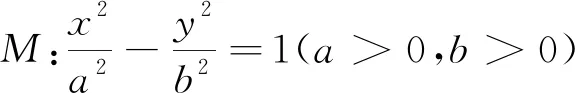
这样拓展操作,我们可以轻松实现从知识“点”到知识“面”的拓展,围绕着“中点弦问题”这个知识“点”作纵深的挖掘,起到巩固和发展的作用.这样的拓展既让学生有兴趣又有挑战性,更方便架构知识的网络.因此,教师要根据高考考试要求,善于对知识点进行适度拓展,引导学生深入思考.
3 反思教学,拓展有法
“数学教学要着重培养学生的数学素养,让学生学会从数学的角度分析问题,用数学的思想方法解决问题.”因此,数学教学中教师要善于适度拓展,丰富、创新教学方式,让学生真正掌握学习数学的方法,促进学生数学素养的提升.
3.1 “链”式追问,“单点”拓展
在精选试题、立足基础、优化运算、找准拓展知识点后,教师通过对问题的引申、层层递进,对问题涉及的知识点进行分析讨论,引向深入,重点突出,自然拓展.可以通过“问题链”的形式,精心设计“问题链”,从易到难,层层深入,引导学生从知识拓展的深度出发,不断深化对拓展知识点的认知.这样的设计有力地牵引着学生正确迅速地掌握新知、理清知识脉络.可以紧扣教学重点,轻松地化解了学生理解中的难点,不仅关注了学生对基础知识和基本技能的掌握,也关注学生思维品质的培养以及意志品质的磨练,还能实现“做一题、会一类”的教学目标,摆脱题海,提升效率;同时提升学生的思维深刻性、灵活性、广阔性.
3.2 找准“标靶”,“串联”拓展
数学是一门逻辑性很强的学科,知识的逻辑体系决定了知识间的联系,这种内在联系为学生掌握新知架起了桥梁,实现各知识点间的“串联”拓展.为了提高各知识间的有效“串联”,我们可以在问题猜想处进行知识点的“串联”拓展,主动拓展探究空间,引导学生主动探索,使学生真正成为探索创造者.认知心理学指出:人的认知结构是平衡的,一旦出现不平衡就会自然产生一种趋力去力求改变这种状态,重新恢复认知系统的内在平衡,即恢复其内在的一致性.因此我们还可以在主要知识概念的矛盾处进行“串联”拓展,拓展学生的积极思维空间.此外,学生学习数学只有通过自身的操作活动和主动参与去做才能产生效果.所以我们还可以在教学关键处进行“串联”拓展,让学生去主动学习,自主建构概念.总之,对学科知识进行拓展的方法是多样的、灵活的,教学时应抓住教学目标,根据课堂教学的需要,在知识拓展的宽度、深度方面灵活设计各类问题,营造一种探究式的数学场景,激发学生的学习兴趣,引导学生主动探索,达到培养学生数学思维、发展学生数学素养的目标.
知识的拓展没有固定的方法与模式,教师作为教学的直接推进者和课堂决策的制定者,应在研究高考试题的基础上,明确主干知识的拓展方向.在知识拓展的方法上,可以根据课堂的预设与生成,通过各种检测数据的积累和综合分析,科学准确地诊断学生知识掌握的优劣,精准剖析问题错因,灵活地在核心知识概念的形成、限用范围、深度提升等方面进行拓展,精心设计各种“问题链”,巩固基础知识和基本技能,破解教学难点,以帮助学生提升数学学科素养.

