基于响应面法的悬拼优化施工中混合梁斜拉桥响应分析

胡豪吴鹤翔孙全胜

(东北林业大学 土木工程学院,哈尔滨 150040)

0 引言

斜拉桥作为大跨度桥梁建设的主要桥型之一,随着跨越能力的提升和实用经济性的比选,混凝土主梁的局限性逐渐增大,以薄壁体系为主的钢梁更为适用。混合梁斜拉桥充分结合了钢材与混凝土的优势。边跨采用混凝土主梁进行锚固和压重,能够缩短边跨的长度。中跨采用钢箱梁,跨越能力和建设条件适应性更强[1]。钢箱梁一般采用预制节段悬拼施工,桥面吊机是主要的起重和悬拼设备。钢箱梁的拼装精度要求高,在悬拼施工过程中,桥面吊机作为施工荷载对钢箱梁的安装线形和成桥线形的影响不可忽略。这增加了斜拉桥设计考虑因素,加大了设计冗余[2]。唐斌华等[3]通过调整桥面吊机前后支撑跨度,有效减小了椒江二桥主梁变形量,实现了精准合龙。邹力等[4]提出钢箱梁“梁重转移”吊装技术,通过减轻吊机前支点反力大幅减小了匹配高差和附加剪切应力。本文通过响应面法对桥面吊机进行参数敏感性分析,通过参数的随机变化,研究桥梁结构响应的变化规律,确定不同参数对桥梁结构响应的影响程度,为设计和施工中桥面吊机的选型计算提供科学依据。传统的参数识别方法基于参数试算的统计分析结果,计算量大且不能够识别参数间的相互影响,存在一定的局限性。近年来,以数理统计和概率论为基础的响应面法在桥梁工程领域得到了广泛的应用与发展。任伟新等[5]利用响应面法修正了结构的有限元模型。钟儒勉等[6]将两阶段响应面模型应用于灌河大桥的多尺度损失识别中,提高了识别精度。李延强等[7]将F检验法与响应面法相结合,实现了对独塔斜拉桥索力的修正。

1 工程概述及有限元模型

某独塔混合梁双索面斜拉桥桥跨组合为340 m+72 m+48 m+32 m。边跨主梁采用预应力混凝土箱梁,中跨为P-K钢箱梁,钻石型桥塔,塔高为197.6 m。钢混结合段设立在桥塔处,保证边主跨的有效连接,主梁为半漂浮体系。斜拉索采用镀锌高强度低松弛平行钢丝斜拉索,标准抗拉强度为fpk=1 770 MPa。拉索按空间扇形布置,最长索长约为344 m。桥型布置如图1所示。

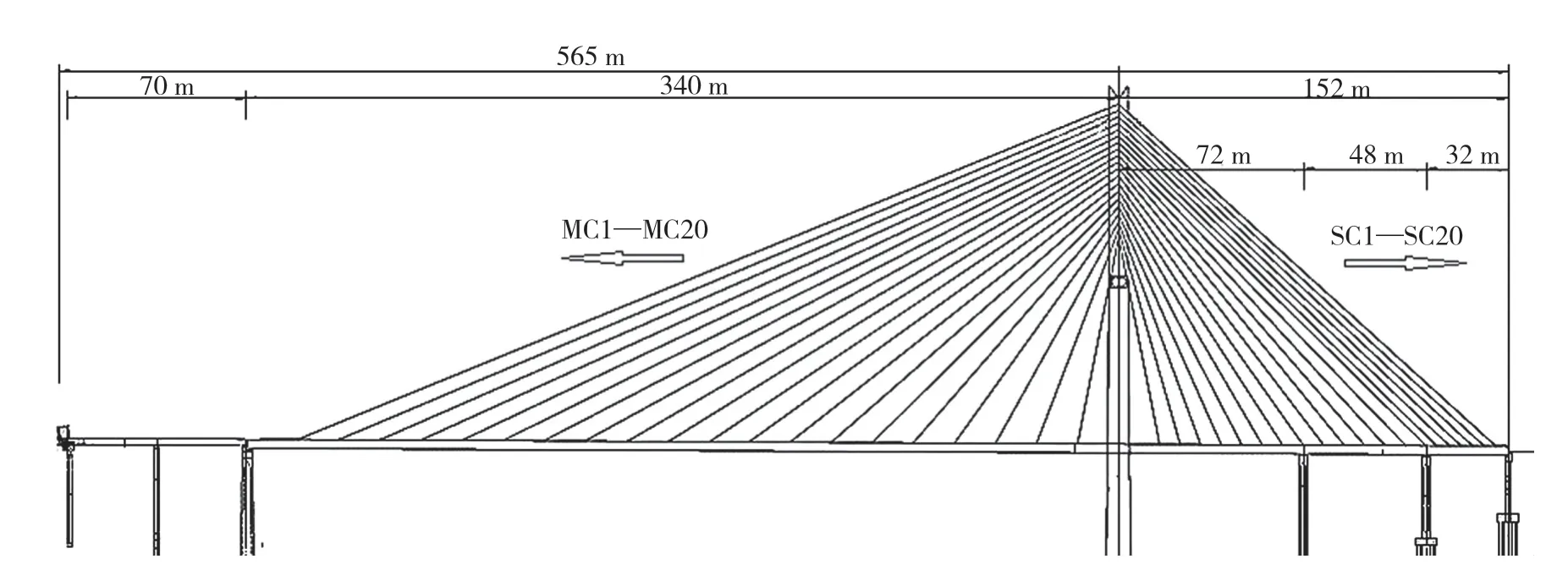
图1 桥型总体布置图Fig.1 Overall layout of bridge type

主跨钢箱梁采用单箱三室斜腹板截面,梁高为3.5 m,顶板宽为32.3 m。钢箱梁共划分为22个节段,标准长度为16 m,内设5道实腹式横隔板,间距为3.2 m,最大节段的重量约为280 t。钢箱梁在工厂预制,运输至桥址处拼装成节段,再采用桥面吊机进行整体悬拼,主要施工流程为:①吊机前移就位;②悬拼Ln+1节段;③张拉斜拉索至初拉力;④重复以上步骤至合龙。桥面吊机工作示意图如图2所示。

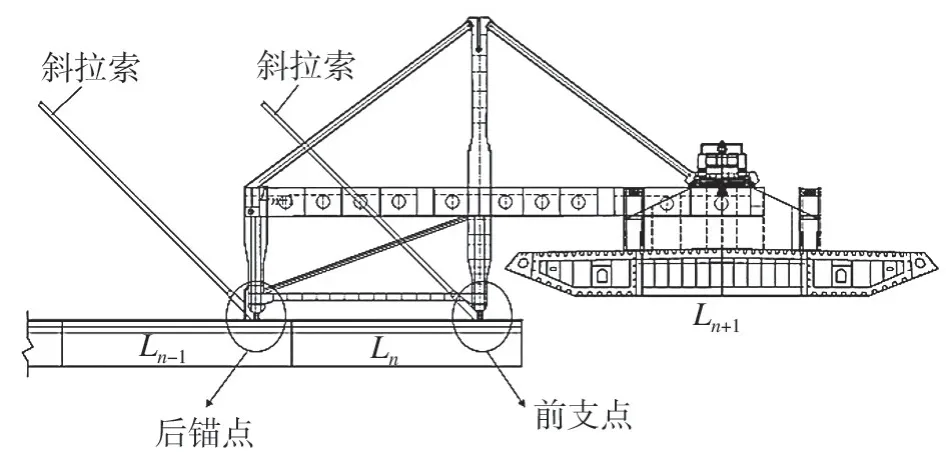
图2 桥面吊机工作示意图Fig.2 Bridge deck crane working diagram

采用Midas /Civil 2021进行施工全过程数值模拟分析,根据实体结构和构件建立计算模型,如图3所示。主梁和主塔采用梁单元,斜拉索采用桁架单元,通过Enrst公式[8]修正拉索的弹性模量,将模型划分为515个节点,418个单元。Enrst公式如下

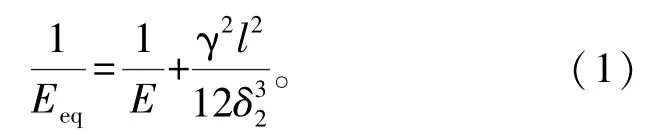
式中:Eeq为斜拉索等效弹性模量;E为斜拉索钢材弹性模量;γ为斜拉索单位体积重力;l为斜拉索水平投影长度;δ为斜拉索索力。

边界条件多支座布置采用“弹性连接+刚性连接”,斜拉索索梁连接和索塔连接为刚性连接,施工阶段塔梁临时固结,在二期铺装完毕后转换成半漂浮体系;钢箱梁在施工阶段分析选用切向安装,保证结构在模拟过程中的受力变化与实际工程一致。通过施加静力荷载和弯矩模拟施工各阶段中桥面吊机吊梁、运梁和悬拼的施工过程。

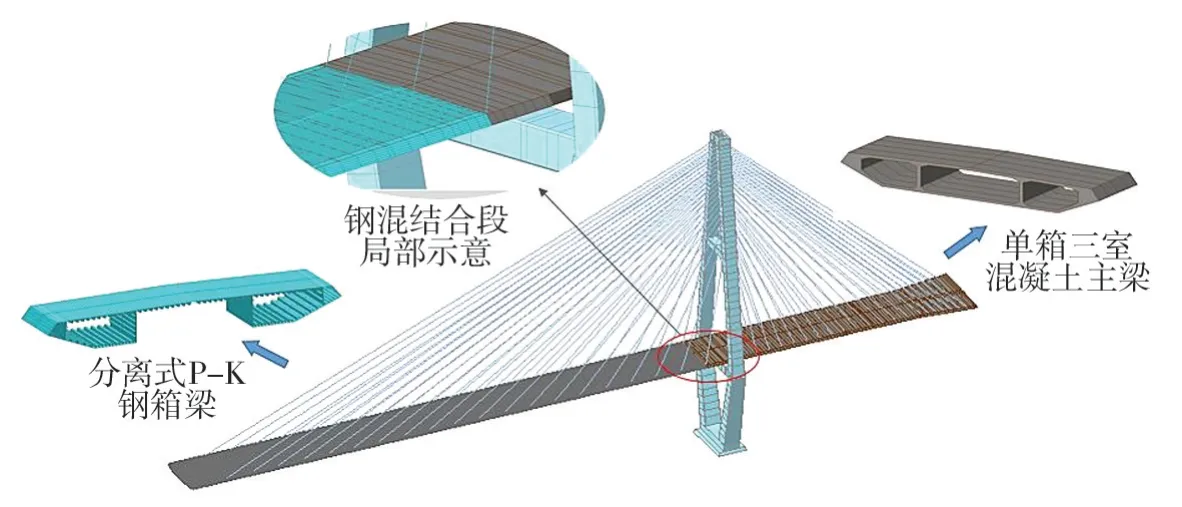
图3 有限元模型Fig.3 Finite element model

2 响应面法参数分析的理论与方法

2.1 RSM基本原理

响应面法( Response Surface Method, RSM)通过设计试验方法获取相应的试验数据,并采用多元多次非线性回归方程拟合试验数据,建立影响因素和响应结果之间的函数关系,以指导多变量优化问题。RSM已经被广泛应用于交通、工业、医药和纺织等工程领域,解决参数选择、配比与优化设计等问题[9-12]。

RSM的基本原理是通过简单的显式函数拟合真实的隐式极限状态函数,得到设计变量与响应值之间的函数关系Z=g(X1,X2,…,Xn),将采用有限元进行大量的试算工作转变成简单的数学问题[13]。考虑斜拉桥体系受力复杂,表征影响因素的设计变量与响应值之间存在非线性关系,结构响应方程采用Wong[14-15]

提出的含交叉项的二次多项式。

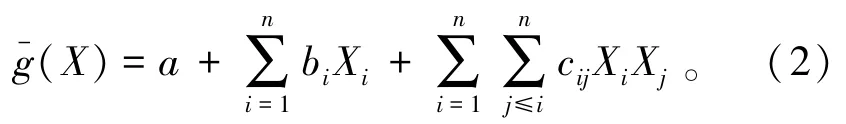
式中:Xi、Xj(i、j= 1,2,…,n) 为设计变量;a、bi、cij(i、j= 1,2,…,n) 为待定因子。

如果采用多元二次回归模型不能够获得拟合函数关系,则可以采用反函数模型、半对数函数模型等高阶非线性模型拟合数据,再对函数Z=g(X1,X2,…,Xn)进行偏微分计算,求出极值点并代入到响应方程中,最后求出函数Z在极值点处的最优解[16-17]。

2.2 取样方法

响应面模型的试验设计方法主要有中心复合设计法(Central Composite Design,CCD)、Box-Behnken设计法(Box Behnken Design,BBD)和均匀设计法(Uniform Design,UN)。前2种方法适用于2～7个因素的试验设计,第3种方法适用于多因素多水平的试验设计。其中,BBD方法具有近似可旋转性,没有序贯性,在因素数量相同的条件下比CCD方法需要的试验次数少,并且能保证相同甚至更好的分析精度和预测效果[18-19]。因此,本文采用BBD方法进行试验设计,设计法如图4所示。

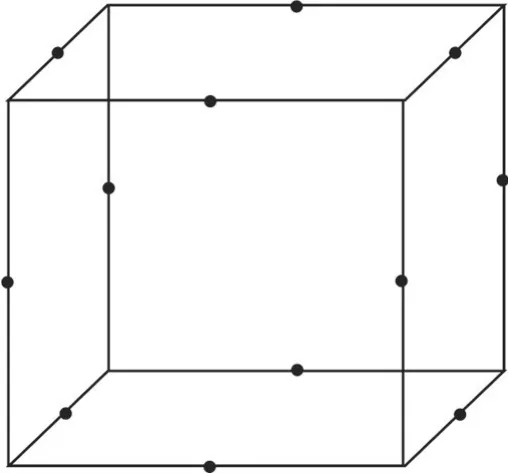
图4 Box-Behnken试验点空间图Fig.4 Box-Behnken test point space diagram

2.3 响应面法试验设计

桥面吊机的设计取决于起吊能力和稳定性,既要满足力学性能的要求,又要具备可靠的安全性和施工性能。

以钢箱梁节段的最大重量280 t作为参考值拟定桥面吊机自重的初始变化范围为200～400 t;以钢箱梁标准节段的长度16 m作为参考值拟定前后支撑跨度的初始变化范围为12～20 m;以桥面吊机设计文件和国内大桥设计案例[20-22]作为参考,考虑最不利条件下桥面吊机前支点承压,后锚点受拉,拟定前后支反力比的初始变化范围为-4～-2;结合工程实际工况和国内相关规范[23-24]拟定钢主梁弹性模量的初始变化范围为2.02×105～2.10×105MPa;具体取值见表1。

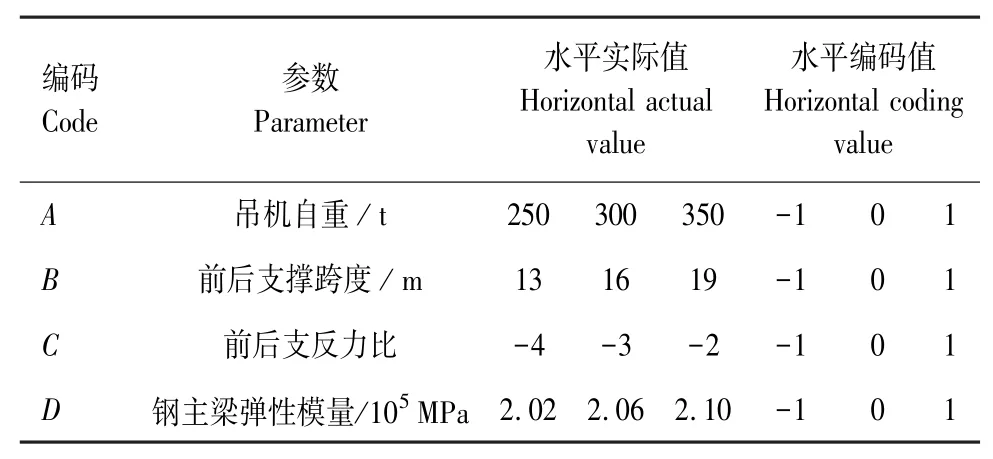
表1 结构参数取值及其编码Tab.1 Structural parameter value and encoding

以最大悬臂状态的主梁挠度R1和成桥状态的主梁应力R2、主梁线形R3、拉索索力R4这4个指标作为结构的响应参数。R1(cm):取最大悬臂状态钢箱梁端部的挠度,上正下负;R2(MPa):取钢混结合段截面上缘的应力,拉正压负;R3(cm):取成桥阶段钢箱梁跨中节点作为主要控制点,上正下负;R4(kN):取成桥状态拉索的最大索力,为MC17。

BBD模型的试验次数同因素的数量相关,多因素BBD模型的试验次数可以用公式(3)表示。

式中:N为试验总次数;k为因素数量;Cp为中心组数,对于4个因素的BBD模型,中心组数量为5,试验总次数为29。将试验设计分组,采用Midas/Civil 2021建立依托工程的模型,并调整结构参数进行计算分析。将因素取值与计算结果汇总,见表2。

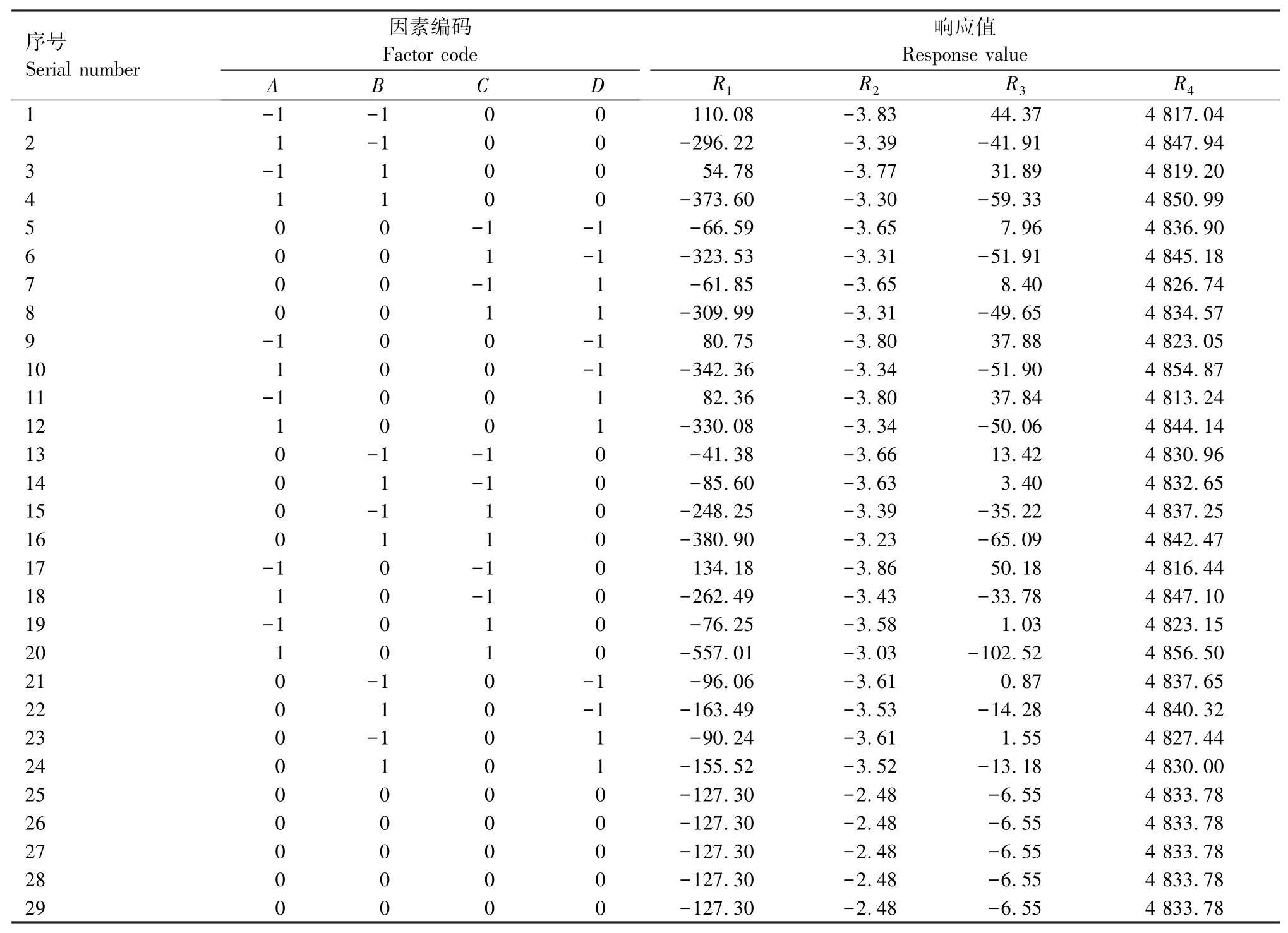
表2 模型因素编码及结构响应值汇总表Tab.2 Model factor coding and structure response value summary table

3 参数敏感性分析

根据结构参数和结构响应结果,运用Design Expert V13软件对BBD模型进行数据建立和二次响应面回归分析。Design-Expert是国际最好的优化试验设计的软件,集成了试验设计、数据分析和可视化结果,在响应面法设计分析方面有广泛的应用,能给出专业、全面、直观的模型和优化结果[25]。

3.1 最大悬臂状态主梁挠度

根据试验结果将施工阶段最大悬臂状态的主梁挠度R1和4个因素进行多元非线性回归拟合,得到如下多元二次响应面回归模型

R1的方差分析见表3。

表3 R1方差分析表Tab.3 R1 analysis of variance table

利用统计学中的方差分析方法对回归模型进行检验,P表示各因素对响应结果的影响程度。一般P＜0.05为显著,P＜0.01为极显著[26]。表3中P小于0.000 1,说明回归模型影响极显著。R2表示模型的决定系数,结果越接近1表示模型计算差异性越小,拟合精度越高。表中R2为0.999 2,说明模拟的响应值与结构的真实值之间误差很小,模型的可靠性高。

从R1的拟合方程和方差分析中的P可以看到,各因素对R1影响程度的由大到小依次为:A＞C＞C2＞B＞BC＞AC,即桥面吊机自重对模型的影响最显著,同吊机自重相比,前后支反力比、前后支撑跨度及其交互作用对模型的影响程度依次降低,钢主梁弹性模量对模型的影响程度不显著。将不显著的因素(P＞0.05)约去并不会影响模型的精度,此时模型的拟合公式为

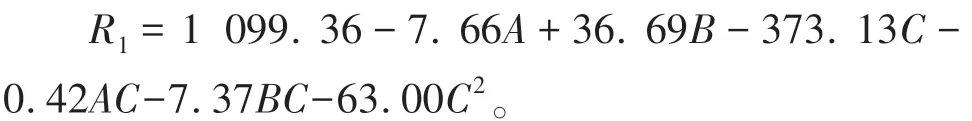
吊机前后支撑跨度和前后支反力比之间,以及吊机自重和前后支反力比之间存在相互作用。2个因素之间的相互作用的曲面图如图5和图6所示。

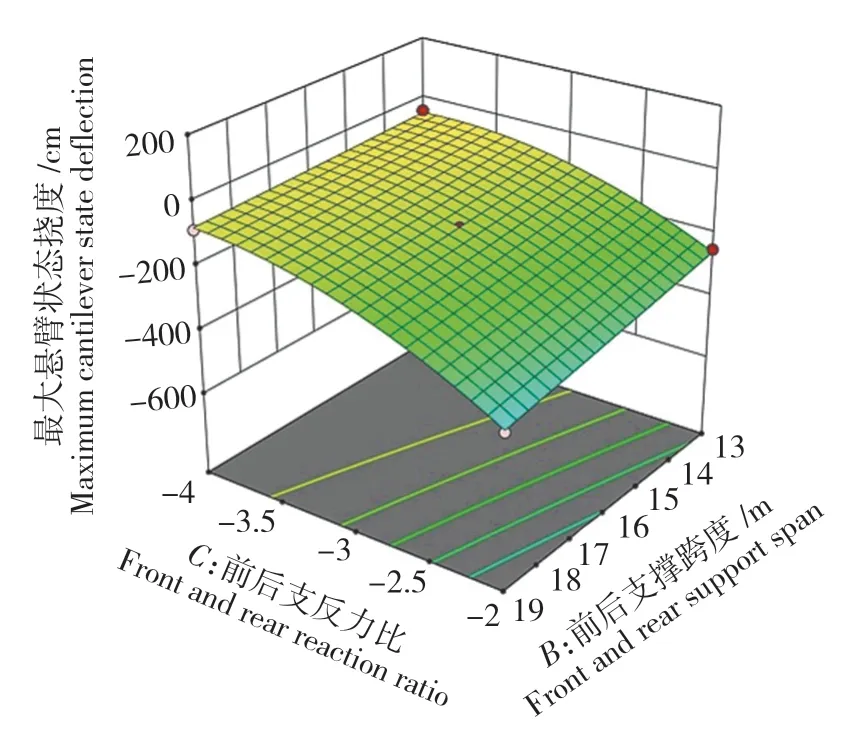
图5 R1:BC相互作用曲面图Fig.5 R1:BC interaction surface diagram

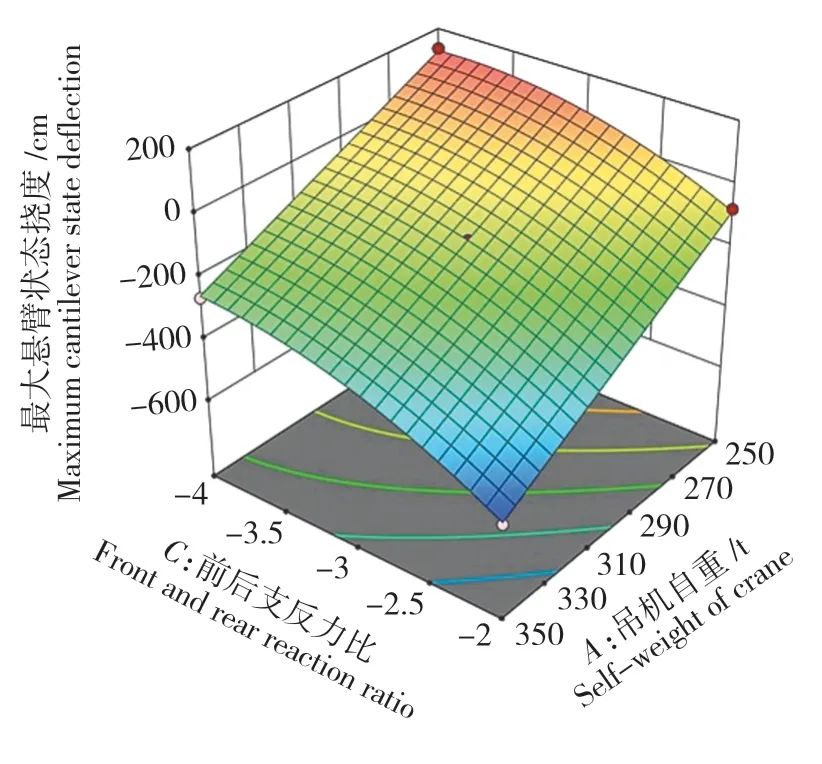
图6 R1:AC相互作用曲面图Fig.6 R1:AC interaction surface diagram

由图5和图6可知,随着前后支反力比的减小,最大悬臂状态的主梁挠度呈现出抛物线状的增大趋势。在结构参数水平因子(C:-3)的作用下,吊机自重每增加10 t,悬臂端挠度增大42.46 cm;前后支撑跨度每增加1 m,悬臂端挠度增大11.64 cm。这说明桥面吊机作用在钢箱梁上前支点的荷载越大、前后支反力比的比值越小、前后支撑跨度越大,主梁悬臂端的挠度越大。

3.2 主梁成桥应力

根据试验结果将成桥状态钢混结合截面上缘处主梁应力R2和4个因素进行多元非线性回归拟合。通过方差分析可以得到D2、A2、B2、C2、A、C、B、BC、AC是对成桥状态主梁应力R2影响最显著的9个因素,并且影响程度依次下降。R2为0.999 8表明模型拟合的程度很好。桥面吊机自重对成桥状态的钢混结合截面应力的影响最大。二次项的影响程度高说明结构的各因素对主梁应力变化的影响呈非线性关系。此时,模型简化后的拟合公式为

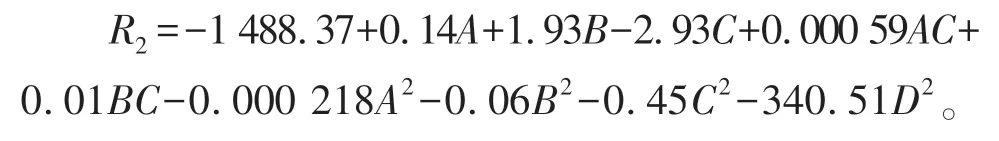
从R2拟合方程和方差分析中可以看到,吊机前后支撑跨度和前后支反力比之间,以及吊机自重和前后支反力比之间存在相互作用。2个因素之间的相互作用的曲面图如图7和图8所示。

由图7和图8可知,在BC相互作用下,随着前后支反力比和前后支撑跨度的增大,主梁内力呈现出抛物线状的变化趋势,先减小后增大。在结构参数水平因子(C:-3,B:16 m)的作用下,成桥主梁的内力最小。这说明在该结构参数的变化区间内存在最佳取值。在AC相互作用下,得到了相似的影响趋势。

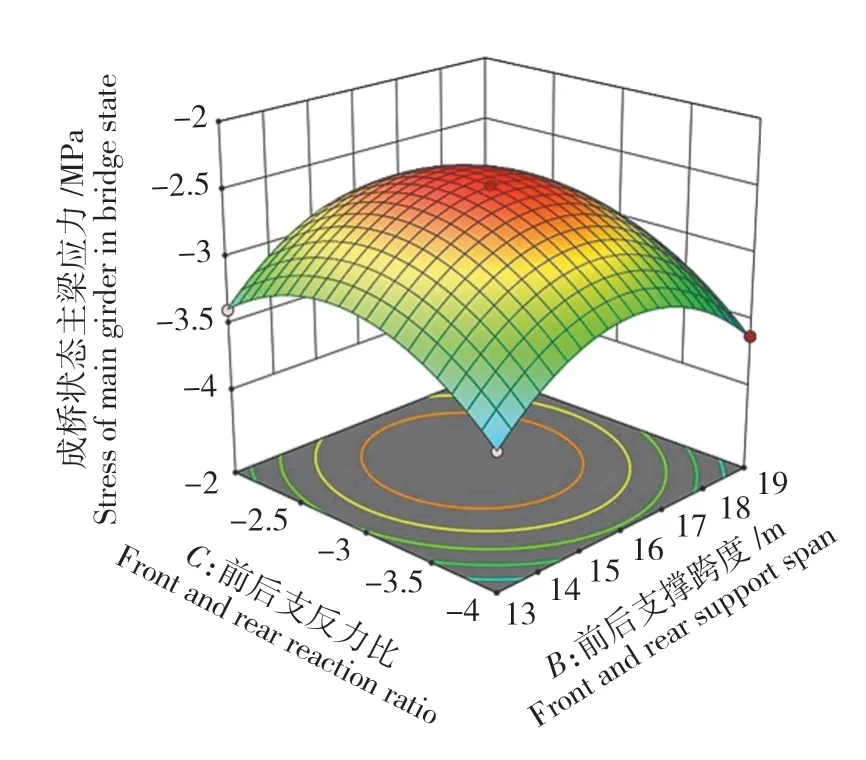
图7 R2:BC相互作用曲面图Fig.7 R2:BC interaction surface diagram

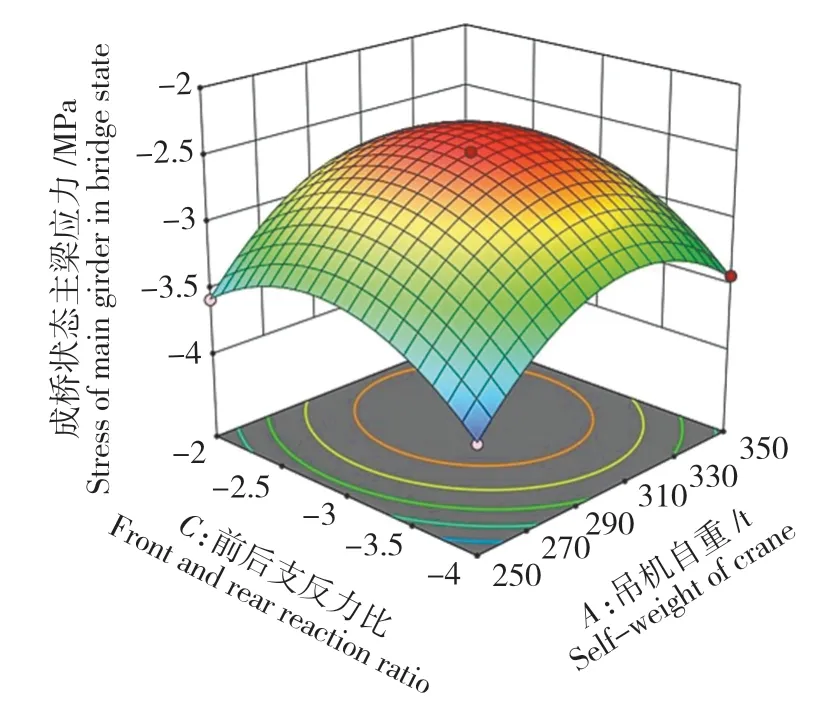
图8 R2:AC相互作用曲面图Fig.8 R2:AC interaction surface diagram

3.3 主梁成桥线形

成桥状态下钢箱梁跨中截面的线形R3响应结果同R1基本一致,将R3和4个因素进行多元非线性回归拟合,桥面吊机自重对模型的影响依然最显著,各因素对R3影响程度的大小同样为:A＞C＞C2＞B＞BC＞AC,R2为0.999 8,模型拟合的程度很好。约去非显著性影响因素,模型的拟合公式为

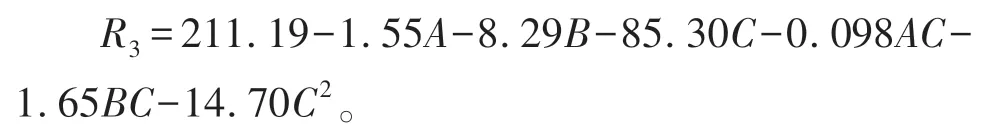
吊机前后支撑跨度和前后支反力比之间,以及吊机自重和前后支反力比之间仍然存在相互作用。2个因素之间相互作用的曲面图如图9和图10所示。

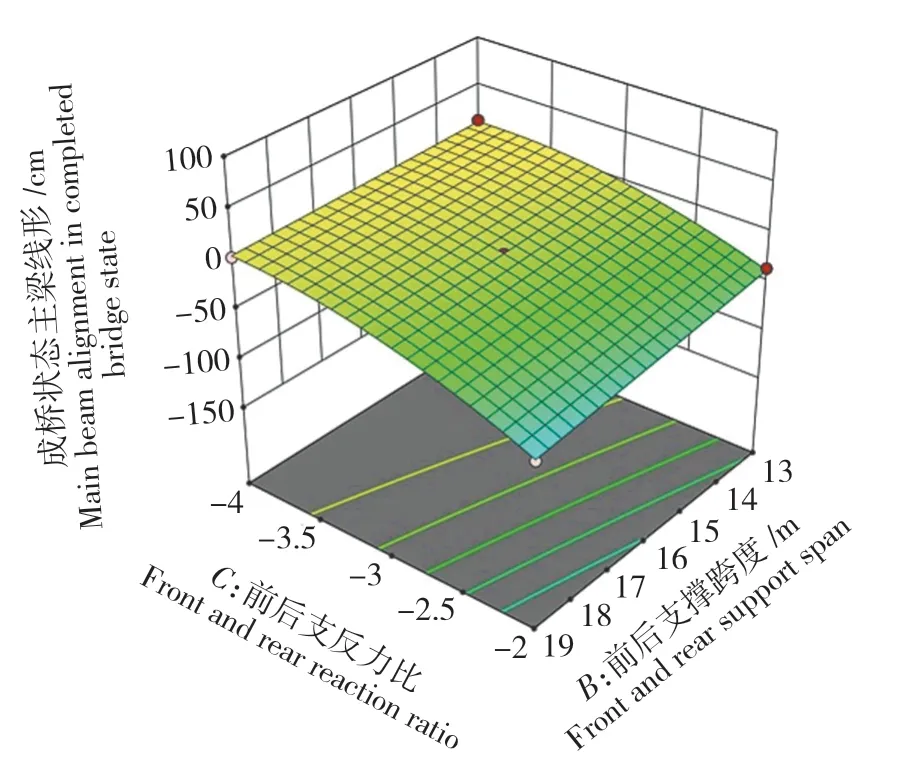
图9 R3:BC相互作用曲面图Fig.9 R3:BC interaction surface diagram

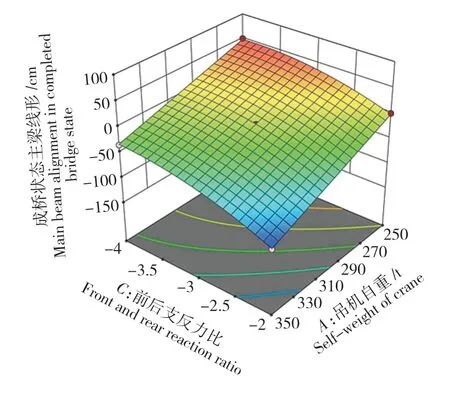
图10 R3:AC相互作用曲面图Fig.10 R3:AC interaction surface diagram

3.4 斜拉索索力

根据试验结果将成桥状态斜拉索最大索力R4和4个因素进行多元非线性回归拟合,通过方差分析可以得到A、D、C、C2、B、BC、AC是对成桥状态拉索索力R4影响最显著的7个因素,并且影响程度依次下降。R2为0.999 8,表明模型拟合的程度很好。钢主梁的弹性模量对斜拉索索力的影响很大,仅次于吊机自重。这说明主梁整体刚度对拉索索力的影响较大。此时,模型简化后的拟合公式为

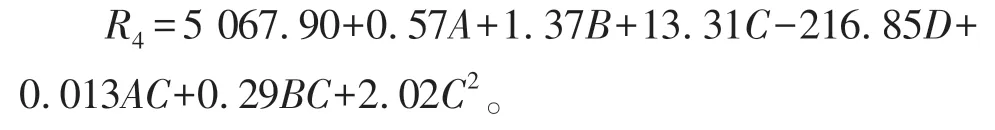
从R4拟合方程和方差分析中可以看到,吊机前后支撑跨度和前后支反力比之间,以及吊机自重和前后支反力比之间同样存在相互作用。2个因素之间的相互作用的曲面图如图11和图12 所示。

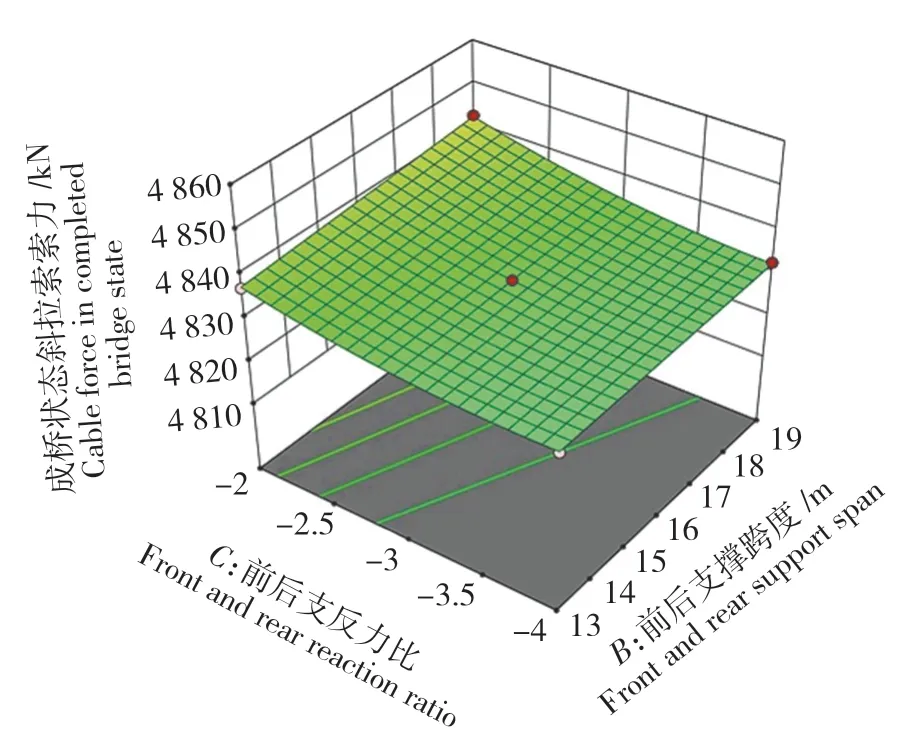
图11 R4:BC相互作用曲面图Fig.11 R4:BC interaction surface diagram

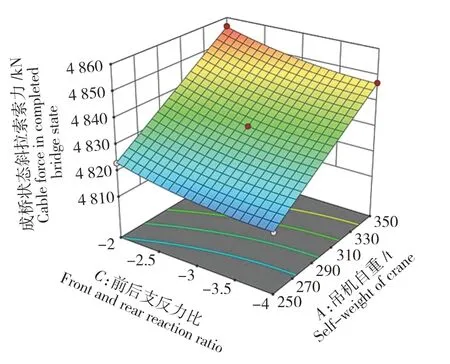
图12 R4:AC相互作用曲面图Fig.12 R4:AC interaction surface diagram

由图11和图12可知,随前后支反力比的增大,成桥状态的斜拉索索力呈现出抛物线状的下降趋势。成桥索力的变化也将引起重要控制量主塔塔偏的变化。在结构参数水平因子(C:-3)的作用下,吊机自重每增加10 t,成桥索力增大3.16 kN,成桥塔偏减小4 mm;前后支撑跨度每增加1 m,成桥索力增大0.45 kN。

4 响应面法优化及工程监测

采用响应面法对桥面吊机的结构参数进行优化。结合工程实际工况和斜拉桥合理成桥状态,拟定钢箱梁的弹性模量为2.06×105MPa,吊机前后支撑跨度为16 m。同时以最大悬臂状态钢箱梁悬臂端挠度为0和成桥状态钢箱梁跨中截面上拱为21.83 cm作为目标优化值,对桥面吊机自重和前后支反力比进行优化。最优参数结果为:桥面吊机自重为283.234 t、前后支反力比为-3.917。将优化后的参数代入斜拉桥模型中进行验算,计算结果汇总见表4。

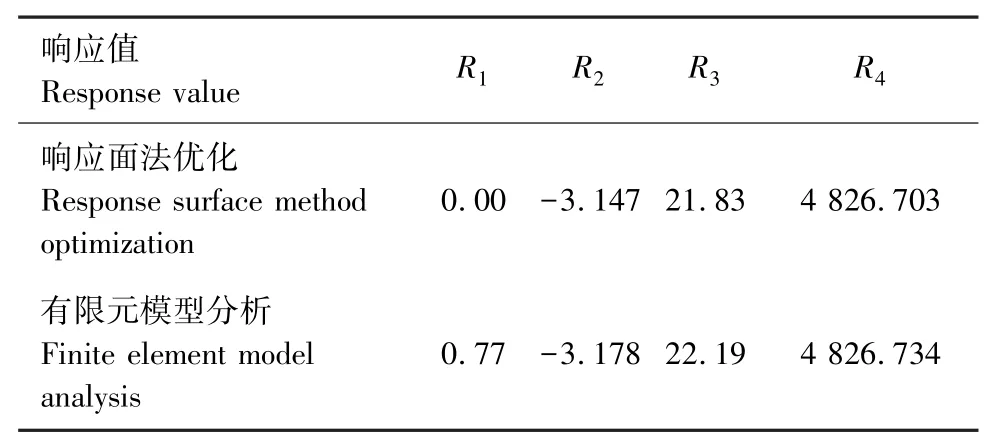
表4 参数优化结果与模型分析结果对比Tab.4 Comparison of parameter optimization results and model analysis results

对比响应面法优化结果和有限元模型分析结果,相对误差很小,最大悬臂端挠度累计差值小于

1 cm。这说明利用响应面法对吊机参数进行优化切实可行且简便有效。

将优化结果和模型计算运用到实际工程中,根据模型分析对施工进行同步监测和数据反馈修正。对钢箱梁悬拼过程进行全桥线形和索力双目标监控,同时对主梁进行应力应变监测,其中钢混结合段应力应变监测如图13所示。监测结果表明,各施工阶段实测数据和理论预测结果基本吻合,选取钢箱梁跨中L11节段张拉前后梁端的挠度、索力和钢混结合段的应力实测数据同理论预测结果进行对比分析,具体见表5。

图13 钢混结合段传感器布设及数据监测Fig.13 Sensor layout and data monitoring in steel-concrete composite section

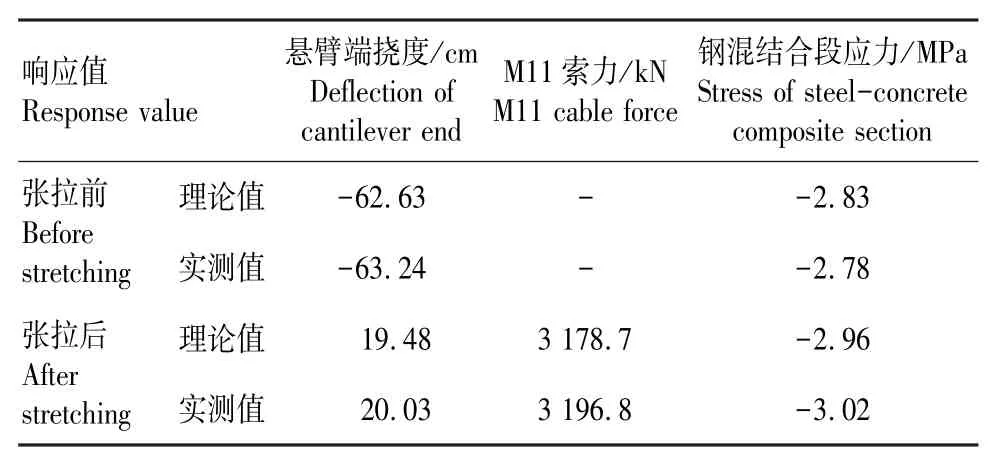
表5 实测值与理论值对比Tab.5 Comparison between measured value and theoretical value

由表5可以得到,梁段张拉前后斜拉桥挠度基本相同,最大线形差为6 mm,M11索力的相对差为0.57%,钢混结合段测试截面上缘应力差为0.06 MPa,均满足监控目标的要求。这说明采用本文的模型对实际工程进行计算分析,结果准确有效。此外,这也证明了本文的理论分析方法和对参数敏感性的研究具备工程应用价值,为实际工程提供了科学的理论依据。

5 结论

以某大跨度混合梁独塔斜拉桥为研究对象,采用响应面法对悬拼施工中桥面吊机的结构参数进行了敏感性分析,主要结论如下。

(1)桥面吊机自重、前后支撑跨度、前后支反力比及其与前述2个参数的交互作用对混合梁斜拉桥主梁线形、内力及成桥索力具有显著影响。钢箱梁弹性模量主要对成桥索力的影响比较显著。

(2)在结构参数水平因子(C:-3)的作用下,吊机自重每增加10 t,悬臂端挠度增大42.46 cm,成桥索力增大3.16 kN,成桥塔偏减小4 mm;前后支撑跨度每增加1 m,悬臂端挠度增大11.64 cm,成桥索力增大0.45 kN。

(3)响应面法能够快速、准确地揭示桥面吊机的结构参数对桥梁线形和内力的影响规律,预测出最优吊机参数方案,为优化桥面吊机结构设计以及在施工过程中监控关键控制量提供了科学依据,对同类型桥梁工程具有借鉴意义。