基于变换核高斯回归模型的无线环境地图构建方法
徐逸群,张邦宁,张晓凯,郭道省
(陆军工程大学通信工程学院,江苏 南京 210007)
0 引言
无线环境地图(Radio Environment Map,REM)能够为认知无线电系统提供多域环境信息和先验知识[1-2],可以用于解决网络规划、干扰协调、功率控制和动态频谱接入等问题。REM构建的基本任务是从空间离散分布的频谱感知设备获取的无线电监测数据,推理没有感知节点位置的信号强度。
现有研究中REM构建的算法主要有近邻(Nearest Neighbor,NN)插值法、逆距离加权近邻(Inverse Distance Weighted Nearest Neighbor,IDW-NN)插值法[3-5]和基于空间统计学的克里金(Kriging)插值法[3,5-10]。其中,NN和IDW-NN没有严密的数学理论支持,但是算法的实现较为简单,易于理解且计算量较小;克里金算法有严密的数学推导,保证了其最佳线性无偏性,但该算法基于平稳性假设,即感知数据之间的相关性仅仅与2点之间的距离相关,该假设是对现实世界的极大简化。这些构建算法都没有考虑复杂环境对电波传播的影响。
近年来,群智频谱感知(Crowd-sourced Spectrum Sensing,CSS)技术受到广范关注[11-12],该技术利用现有移动通信网络中的移动通信终端来执行频谱感知任务。NN能够提供海量数据,如何从这些数据中提取有用信息,提升REM构建的准确性,值得深入研究。
REM构建的准确性,受到2个重要因素的制约:一是所研究的环境的复杂性,复杂的地形地物对电波传播的影响较大,待估计位置的信号与已测量位置的信号之间的相关性受到不同环境的影响呈现出空间异构的相互关系;二是采集数据的位置和数据量,一方面需要更多的数据以提升准确性,另一方面在实际监测系统中,采集更多数据带来额外的系统开销,提升了数据处理分析难度。因此,需对数据采集的位置进行优化,在提升准确率的同时尽可能减少冗余数据。
本文提出一种新颖的基于变换核高斯回归模型的REM构建算法,该算法以高斯过程(Gaussian Processes,GP)为基本框架,考虑了环境异构性对REM构建的影响,能够从群智感知数据中学习环境异构性信息。此环境异构性信息是进行空间数据选择的重要前提,因此在所提模型基础上,利用获取的空间异构性信息,提出了2种无线电频谱监测空间选点方案,进一步提升REM构建的准确性,并通过数据选择降低系统开销和数据冗余。
1 系统模型和问题描述
1.1 系统模型
对某二维平面空间内群智感知设备的数据进行研究,不失一般性,假设此二维平面区域为1 km×1 km的范围。区域内的感知设备将其位置和测量的接收信号强度上报给融合中心。
REM构建的主要任务是推理没有感知设备位置的信号强度,进而绘制该区域的功率谱密度图。在实际信号强度测量过程中,采用长期测量的方法以消除小尺度衰落和噪声的影响,得到的平均接收信号强度可分解为3个部分,分别为自由空间传播路径损耗、阴影效应和测量设备导致的误差,如式(1)所示:
(1)
式中,Pt为发送功率;d0为参考单位距离;λ为波长;η为自由空间传播损耗因子;Lt为信号源位置;lj为第j个感知设备的位置;Sj为信号源至第j个感知设备的阴影衰落分量;Nj为第j个感知设备的测量误差。
1.2 问题描述
自由空间传播损耗可以通过链路计算得到,因此REM构建的困难在于阴影效应引起的电波传播变化。在无线通信系统中,考察单个接收点的阴影效应时,通常将其建模为一个服从对数正态分布的变量。文献[13]针对空间阴影效应的空间相关性进行了详细的研究,通过将构建的空间损耗场模型与实测数据对比,证明了发射源相同而接收点接近时,空间阴影效应有较强的相关性。有学者将这种相关性运用于REM的构建中[8-9],以提升REM构建的准确性。
以前的研究中,空间相关阴影效应被建模为一个各向同性且平稳的过程,此假设可以等同为假设电波在空间中传播受到的影响是相同的,即传播环境是匀质性的。而实际上,电波传播环境十分复杂,特别是在城市区域,由于信号传播的阴影效应影响,不同位置数据之间的相关性不仅仅取决于二者之间的距离。复杂的环境提升了空间推理的难度,由于环境的异构性,要提升REM构建的准确性,应将空间内阴影效应分量建模为各向异性和非平稳的过程。本文研究的算法旨在表征环境的异构性,以进一步提升空间频谱推理的准确性。
此外,由于数据的空间相关性,某一点的数据可以提供其临近点的信息。从信息熵的角度考虑,在空间内每增加一个感知节点,即可降低该区域的不确定性。然而,当区域内感知节点密集到一定程度时,新增节点提供的信息熵越来越小,增加感知节点的性价比逐渐降低。同时,由于环境的非匀质性,在某些地形、地物环境不太复杂的区域内,只需要少量的感知设备即可表征该区域内的信息;而在地形、地物环境较为复杂的区域内,则需要布置更多的感知设备。由于空间环境的复杂性,实际应用中,监测数据的空间位置也会对REM构建结果产生影响。因此,应根据环境异构性信息设计相应的频谱监测设备的选点方案。
2 变换核高斯回归模型
REM构建的本质是一个复杂的回归任务,而GP由于其灵活性,特别适用于此类任务。作为机器学习领域的一个重要工具,GP近来年得到了广泛的研究[14-18]。
GP回归参数的训练通过最大化边际似然函数来完成。边际似然函数表示为:

N(y|0,Σθ),
(2)
则负边缘对数似然函数(Negative Log Marginal Likelihood,NLML)表示为:
L(θ)=-lnp(y|X,θ)=
(3)
式中,det(·)表示矩阵的行列式。
GP训练过程被构建为下列非凸优化问题:
(4)
通常,使用基于梯度下降的优化算法,寻找NLML的最优解。
GP的核函数隐含了关于建模的函数f所属类别的假设[17],等同于学习算法中的“归纳偏好”。在此意义上,关于模型的先验知识,可以通过GP的核函数嵌入到GP回归模型中。有一些常用的基础核函数,如线性核函数、径向基函数核函数、周期核函数、Matern核函数和谱混合核函数等[18]。核函数的设计和选择对GP回归模型的性能有很大的影响。例如,线性核函数推断出的模型函数f为线性函数,周期核函数推断出的模型函数f具有周期化的结构。
Wilson提出的深度核学习(Deep Kernel Learning,DKL)将深度架构的表示能力封装到GP中,具有利用数据学习核函数的能力。DKL从一个参数为θ的基本核函数k(xi,xj|θ)开始,利用权重参数为w的深度神经网络(Deep Neural Network,DNN)对原输入进行非线性变换,将基础核函数转化为:
k(xi,xj|θ)→k(h(xi,w),h(xj,w)|θ,w),
(5)
式中,h(·)为DNN的非线性变换。DKL大幅度提升了GP的表示能力,并通过优化GP的边际似然函数为核函数提供自动学习功能。但是,在某些情况下,DKL算法的稳定性较差,GP会尝试利用DNN的灵活性在所有的输入数据之间建立相关性,同时DKL中的DNN容易产生过拟合[19]。
在GP中引入非平稳性的一种方法是引入一个非线性变换h(x),将空间D中的输入x变换到一个新的空间D′中[14]。在DKL中,DNN是用于变换输入空间的非线性变换,且该线性变换由DNN的权重参数表征。然而,在空间频谱推理问题中,模型的输入是感知设备的位置信息,所表示的空间是实际的物理空间。用DNN对该空间进行非线性变换易引起空间折叠效应,不适用于本节研究问题中的物理量。因此,DKL虽然有强大的表示力和从数据中学习核函数的能力,但不适用于REM构建问题。
受到DKL的优缺点的启发,解决REM构建问题应设计一个具有以下特性的非线性变换:
① 非线性变换能够通过一些参数来表征,通过变化参数值可以改变非线性变化的形态,以使其具有一定的表示能力,可以灵活地表示各向异性和非平稳性;
② 非线性变换应是单射,具有拓扑同胚性,从而不会引起空间折叠效应。
通过设计3种简单的具有上述特性的非线性变换,并将这3种简单的非线性变换组合起来,可以构造一个灵活的非线性变换来表征空间异质性。下文将详细说明这3种变换。
为了清楚表述,某一点在二维空间的位置表示为s=(s1,s2);α,β和γ表示非线性变换的超参数,超参数的值在模型设计时根据具体研究问题的范围和复杂度选择确定;用w和w,或二者加下标表示的权重参数决定非线性变换的具体形态,权重参数的取值在模型训练过程从感知数据中学习获得。
2.1 坐标轴变换单元
坐标轴变换单元(Axial Transformation Unit,ATU)是指对多维数据的其中一个维度(即其中一个坐标轴)进行独立的非线性变换,通过一下步骤实现:
① 以二维空间为例,将输入数据的位置坐标信息归一化至[0,1]或[-1,0],为方便区分,可以将横轴归一化至[0,1],纵轴归一化至[-1,0]。
② 对某个维度的ATU通过一系列基函数φ(sk)的加权和来实现,ATU的基函数如图1(a)所示,分别对2个维度进行坐标轴变换的示例如图1(b)和图1(c)所示。其中,第一个基函数斜率为1的线性变换函数φ1(sk)=sk,其余基函数为平移的Sigmoid函数:

(a)ATU的基函数
(6)
式中,参数αi1决定了Sigmoid函数的梯度;αi2决定了Sigmoid函数的偏移位置;r为Sigmoid函数的数量,决定了在[0,1]内非线性变换的分辨率,该分辨率也决定了非线性变换的表示能力,当环境较为复杂、局部特征较多时,可以增大该分辨率,用更多的Sigmoid函数构成非线性变换。
③ 将变换后的值归一化至[0,1]或[-1,0]。
由于Sigmoid函数的单调性,如果将所有权重参数限制为正值,则可以保证ATU是由[0,1]→[0,1]或[-1,0]→[-1,0]的单射非线性变换,且该变化具有一定的灵活性,可以通过权重参数控制变换的具体形态。维度1的ATU计算结构如图2所示,其中表示归一化。

图2 维度1的ATU计算结构
综上,将对输入向量的第k维的ATU定义为:
(7)
(8)
式中,
(9)
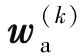
2.2 径向基函数变换单元
径向基函数变换单元(Radial Basis Function Transformation Unit,RBFTU)是对原空间局部扩展或者压缩,该变换定义为:
fr(s;wr,β,γ)=s+wr(s-γ)e-β‖s-γ‖,
(10)
式中,超参数γ=(γ1,γ2)是局部扩张或者压缩的中心点;超参数β可以控制局部扩展或者压缩的边界;权重参数wr决定扩张或者压缩的程度。若将权重参数wr限制在(-1,e3/2/2),则可确保该变换为单射[20]。RBFTU的计算结构如图3所示。

图3 RBFTU的计算结构
中心位置在(0.25,-0.125)的RBFTU示例如图4(a)所示,通过选择不同的超参数γ和β,并将不同的RBFTU级联在一起,可以构造整个空间范围内不同局部压缩和扩张的非线性变换,如图 4(b)所示。研究环境较复杂时,可以增加级联的RBFTU的分布密度。

(a)单个径向基函数变换的影响区域范围
2.3 莫比乌斯变换单元
莫比乌斯变换是在复平面上的一对一的可以映射到自身的保角变换[21]。令z=s1+s2j,(j2=-1),莫比乌斯变换单元(Mobius Transformation Unit,MTU)可以定义为:
fm(s;wm)=(R[gm(z)],I[gm(z)]),
(11)
式中,
(12)
a,b,c,d是满足ad-bc≠0的复数。MTU的权重参数为:
wm=[R(a),I(a),R(b),I(b),R(c),I(c),
R(d),I(d)]。
(13)
MTU的计算结构如图5所示。

图5 MTU的计算结构
MTU变换一个二维空间D2=[0,1]×[0,1]内的一个正方形棋盘形状的示例如图6所示。从式(12)可以推导出gm(-d/c)=∞,因此,为了确保D2内的点不会映射至∞,必须将-d/c限制在复平面上由点[0+0j,0+1j,1+1j,1+0j]包围的区域内。

图6 MTU示例
上述3种基本变换单元都满足本节提出的2种基本性质,可以作为构建二维空间内的复杂非线性单射同胚变换的基本模块。可以根据实际应用场景的不同,设计并选择这些变换的不同组合对原空间内的核函数进行变换。同时,所有的权重参数:
(14)
可以与GP的基础核函数的参数一起,通过最小化GP的NLML,从数据中学习得到参数的具体取值。
变换核高斯回归(Transformed Kernel Gaussian Process Regression,TKGPR)模型如图7所示。构建的TKGPR模型包含维度1的ATU、维度2的ATU、一系列的RBFTU的级联和一个MTU,这些基础变换一起构建出对原始二维空间的单射非线性变换,最后,将变换后的结果输入GP得到输入点的信号强度的概率分布。

图7 TKGPR模型
组合成的非线性变换可以用复合函数表示为:
(15)
从仅有参数σ2和l的基础核函数:
(16)
开始,用非线性变换转换原始核函数:
k(si,sj;σ,l)→k(h(si;W),h(sj;W);σ,l,W),
(17)
式中,h(s;W)为由参数W决定的合成的非线性映射。
将此算法命名为变换核学习(Transformed Kernel Learning,TKL)。在实际应用中,可以根据研究区域的情况选择基本变换的组合方式以及每个基本变换单元的超参数的数量,使得模型的复杂度与待研究区域内环境的复杂度相一致。
3 两种基于TKGPR模型的分布式频谱监测空间选点算法
使用群智感知数据进行REM构建主要存在以下几点问题:① 群智感知终端是利用用户移动通信设备进行数据采集,设备能力较弱、数据精确度不高;② 大量群智感知设备提供了大量的冗余数据,在模型训练阶段大量的数据可以更好地训练GP模型,而在REM预测阶段冗余数据提供的信息量有限,带来了数据处理的计算压力;③ 由于用于终端运行感知任务会带来额外的电量消耗,用户不愿意长期运行于数据感知状态,虽然有学者针对群智感知设备的运行成本进行优化设计,但利用大量用户长期进行感知还是会产生额外的经济消耗。
针对上述问题,本节研究的场景为:在模型训练阶段,通过利用N个群智感知节点的数据结合TKGPR模型获取当前研究区域内的环境异构性信息,即该区域内的变换核函数参数。由于区域内的地形、地物短时间内变化较小,可以近似为不变。因此,估计出的变换核函数参数可以继续用于REM的构建过程。在构建阶段,考虑采用2种方式:一种是设置专用的频谱采集设备获取更高精度的测量数据,在此区域内布置k(k≪N)个专用的监测节点以取代群智监测的方法;另一种是在大量群智感知中选择k(k≪N)个点的数据用于空间推理,获取实时的REM状态,以降低数据获取成本和需处理的数据量。
本节提出2种基于TKGPR模型的频谱监测空间选点算法,分别为基于贪婪算法的互信息最大化(Greedy-based Mutual Information Maximum,GMIM)空间选点算法和基于变分推断(Variational Inference,VI)的空间选点算法。
2种选点算法同样基于GP,GMIM利用GP模型的核函数进行选点,将训练产生的核函数作为算法的输入条件。GMIM算法流程如图8所示。VI算法是通过改变GP回归模型的优化目标进行选点,将TKGPR模型训练过程和空间选点过程结合起来,以证据下界(Evidence Lower Bound,ELBO)作为算法优化目标以自动完成空间选点,基于VI的选点算法流程如图9所示。下面详细阐述2种空间选点算法。

图8 GMIM算法流程

图9 基于VI的选点算法流程
3.1 基于贪婪算法的互信息最大化空间选点算法
首先,将研究区域网格状离散化,并将选点问题定义为:在R2空间内的有限大小的子集V内选取k个最优的位置,其中V为离散化得到的可能选择的位置,假设选择的最优的k个点组成集合A,则没有感知设备的点表示为VA。网格状离散化点集示意如图10所示,空间离散化的所有点构成点集V,红色点为点集A,蓝色点为点集VA。

图10 网格状离散化点集示意
将空间选点的优化目标定义为选择的k个点能够尽可能预测没有感知节点位置处的数据,即寻找一个A*能够最大程度降低没有感知设备位置处数据的熵:
(18)
式中,H(·)为随机变量的熵。式(18)等同于最大化点集A处的随机变量和点集VA处随机变量的互信息量I(yA;yVA),为简化表示,定义选择点集A后的互信息量为:
MI(A)=I(yA;yVA)。
(19)
对互信息量进行优化是一个NP-完全问题,无法在多项式时间内找到最优解,因此,考虑采用贪婪算法逐个增加监测点以获取此问题的次优解。假设下一个选取的点为z,最大化增加该点后提升的互信息量:
MI(A∪z)-MI(A)=H(yA∪z)-H(yA∪z|yV(A∪z))-
[H(yA)-H(yA|yVA)]=
H(yA∪z)-H(yV)+H(yV(A∪z))-
[H(yA)-H(yV)+H(yVA)]=
H(yz|yA)-H(yz|yV(A∪z))。
(20)

(21)
基于贪婪算法的互信息最大化监测设备选点算法如算法1所示。

算法1:基于贪婪算法的互信息最大化监测点选择算法输入:协方差矩阵ΣVV,监测点数目k,可选位置集合V输出:选择的监测点位置集合A1:将集合A设置为空集∅2:for j=1→k do3: for z∈VA do 4: δz←σ2z-ΣzAΣAAAA-1ΣAzσ2z-ΣzA-ΣA-A--1ΣA-z5: end for6: z∗←argmax7: A←A∪z∗8:end for
3.2 基于变分推断的空间选点算法
在研究空间内需要选择M个点,假设这些选择的测量点组成的向量为:
Z=[z1,z2,…,zM],
(22)
这M个点的取值可以表示为:
u=f(Z)。
(23)
为了使从这M个点的数据得出的高斯过程f的后验分布尽可能接近利用所有的数据得到后验分布,假设qφ,θ(f)为通过数据(Z,u)得出的f的后验概率分布,φ为引入的变分参数,该参数包括分布qφ,θ(f)的均值、方差,以及M个点的位置信息。为了使得qφ,θ(f)尽可能接近利用所有数据获取的后验概率分布,使用KL散度表征其与所有数据的后验概率分布pθ(f|y,X)的距离:
KL(qφ,θ(f)‖pθ(f))-lnpθ(y|X)。
(24)
调整式(24)两边各项位置可得:
KL(qφ,θ(f)‖pθ(f)),
(25)
式(25)左边第1项为GP的对数边缘似然函数(Log Marginal Likelihood,LML),第2项为从m个数据得到的f的后验概率分布与所有数据得到的f的后验概率分布的KL散度;式右侧定义为ELBO[14]。由于KL散度的取值为非负值,当:
qφ,θ(f)=pθ(f|y,X),
(26)
时,左侧的KL散度取值为0,ELBO的值等于对数边缘似然分布,因此ELBO为LML的下界。在GP中,通常设置LML为优化目标,将问题转化为优化对数边缘分布的下界,即:
(27)

(28)
式中,第I部分可以通过下列推导表示为:
(29)
因此,式(28)可表示为:
KL(qφ(u)‖pφ,θ(u))。
(30)
假设变分分布为多元高斯分布:
qφ(u)~N(μu,Suu),
(31)
则式(30)右侧可以用闭式表达式表示。同时,式(30)表明,可以使用批量梯度下降算法,完成模型的训练。在优化ELBO的同时,可以得到TKGPR模型各个参数的取值,以及变分参数的取值,其中包括各个点的位置信息。
4 仿真结果和分析
4.1 REM构建仿真
4.1.1 模型构建
选择TKGPR模型的超参数如下:2个ATU的分辨率取值都为20,级联的RBFTU以9×9的方式均匀分布在二维空间内,每个RBFTU的边界与临近RBFTU的中心点相交以确保变换对整个区域的覆盖,选择径向基函数(Radial Basis Function,RBF)为GP的基础核函数。按此方法构建的TKGPR模型有133个控制参数。每个ATU有21个参数,级联的RBFTU共有81个参数,MTU有8个参数,RBF核函数有2个参数。在实际使用中,可以根据研究问题的复杂度选择构建空间非线性变换的参数数量。
4.1.2 训练和推理过程
TKGPR模型的训练集为{X,y},X为群智感知设备的位置,y为接收信号强度。利用反向传播算法进行模型训练,并借助“PyTorch”用GPU加速训练模型训练过程。根据式(3)和式(17),将TKGPR的NLML作为损失函数,可以表示为:
(32)
通过链式法则得到参数的梯度:
(33)
最后,利用训练好的模型参数,可以得到无感知终端位置处的接收信号强度的预测分布。该预测分布不仅仅得到预测的结果,同时还提供了结果的不确定性度量,这是GP优势之一。
4.1.3 性能分析对比
在仿真分析中,模拟了区域为1 km×1 km范围内180×180个点的阴影效应分量,并选择该区域内均匀随机分布的若干点作为群智感知设备的感知数据。利用感知数据,采用NN、IDWNN、普通克里金(Ordinary Kriging,OK)、GP和本节提出的TKL算法,恢复了该区域内阴影效应分量。实验表明,当NN和IDWNN算法参与计算的邻居节点数量大约为20时,其估计性能较好,因此选择邻居节点数为20与其他算法进行对比。OK算法的性能由选择的变差函数形式决定,本文参考文献[8]使用指数半变差函数。
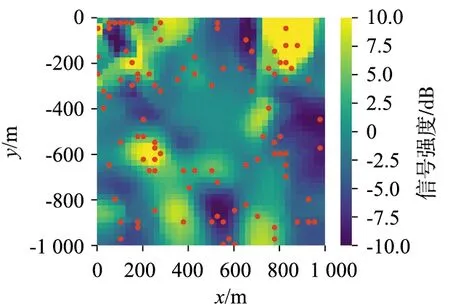
使用500个群智感知设备,用不同算法恢复的区域内的阴影效应及真实阴影效应的对比如图 11所示,图11(a)为群智感知设备的观测值,图11(b)为真实的阴影效应分量,图11(c)~图11(g)分别为NN,IDWNN,OK,GP及本节提出的TKL算法的恢复结果,该图提供了不同算法空间推理结果的直观印象。

(a)测量点数据
进一步,通过与实际阴影效应分量进行对比,用4个指标衡量算法的性能,分别为均方根误差(Root Mean Square Error,RMSE)、连续分级概率评分(Continuous Ranked Probability Score,CRPS)[22]、正确检测区域比例(Correct Detection Zone Ratio,CDZR)和虚警区域比例(False Alarm Zone Ratio,FAZR)[1]。
RMSE用于评估点估计的结果,CRPS将平均绝对误差推广至概率预测场景下,是一种广泛应用于当预测结果为概率分布而观测结果为确定值时的评价指标,可以理解为预测分布与在真实确定值点处的退化分布之间(单位阶跃函数)的平方积分距离:

(34)

不同算法RMSE和CRPS随群智感知设备数量变化的曲线如图 12和图 13所示。

图12 不同算法RMSE随群智感知设备数量变化的曲线

图13 不同算法CRPS随群智感知设备数量变化的曲线
可以看出,GP和OK算法的RMSE大致相同,而GP有更好的CRPS。由于GP和OK算法都基于环境同质性的假设,因此预测分布的平均值大致相同。当群智传感器的数量大于 400 时,所提出的 TKL算法优于所有其他算法。TKL 算法可以从感知数据中学习环境信息,并将此信息隐含在非线性变换的参数中,为其准确性提供了性能增益。当群智感知设备的数量较少时,TKL算法性能较差,这是因为局部区域内的感知设备太少,导致算法无法捕捉到环境的异质性。
CDZR和FAZR的对比分析如图 14和图 15所示,分别展示了不同算法的CDZR和FAZR随研究区域内群智感知数量变化的曲线。同样,当研究区内的群智感知设备的数量超过400,算法可以捕捉到局部环境的异质性时,提出的TKL算法的CDZR高于其他算法。TKL算法的FAZR略低于OK和GP算法,但若将FAZR和CDZR联合起来进行评估,可以发现,算法以较小的FAZR损失换取了较大的CDZR的提升。这也符合认知通信系统的设计原则,即避免对主用户的影响比频谱利用机会的提升更加重要。

图14 不同算法CDZR随群智感知设备数量变化的曲线

图15 不同算法FAZR随群智感知设备数量变化的曲线
同时,在模型训练过程中发现TKL算法不易过拟合,它保留了GP不易过拟合的固有特性[14]。另外,与DKL中的DNN不同,TKL算法中的非线性变换受限于几种单射映射,增加了GPR模型的灵活性,而不会引起DKL中的病态效应[19]。在这些算法中,TKL 的复杂度最高,但由于网络和数据采集技术的发展,可以获取的数据量呈爆炸式增长,且计算机的算力也在不断得到提升。因此,此类算法的实现成为可能,具有很好的应用前景。
4.2 空间选点算法仿真结果和分析
4.2.1 仿真实验设置
在GMIM算法中,需要从有限的点集内选择频谱监测点,因此将研究空间离散化为40×40的栅格状点阵,作为待选择的频谱监测点集V,从中选择100个监测点。在模型训练阶段,使用2 000组群智感知数据,训练TKGPR模型,以获取研究区域内的1 600个栅格点的协方差矩阵,作为GMIM算法的输入条件。
在VI算法中,使用同样的2 000组群智感知数据,将待选点的初始位置设为10×10矩形栅格状均匀分布的点,通过优化ELBO在训练TKGPR模型的同时,优化这100个点的位置变量。
区分2种应用场景,将所提算法与均匀随机选点进行分析对比。2种应用场景分别为:① 监测点和待估计点为有限个离散点集时;② 监测点选择的自由度较高,而需要使得整个区域内推理的平均误差较低时。
对5种情况进行了仿真实验,分别为:
① GMIM算法选择点集A后,对点集VA处的数据进行推理;
② 在点集V中均匀随机选点选择点集A后,对点集V/A处的数据进行推理;
③ GMIM算法选点后,对整个区域进行推理;
④ VI算法选点后,对整个区域进行推理;
⑤ 在整个区域内均匀随机选点后,对整个区域进行推理。
4.2.2 选点结果和性能对比
图 16为真实阴影效应,可用于与不同算法的频谱推理结果进行对比。图 17~图 21为上述5种场景下的选点和空间频谱推理结果。通过与区域内真实的阴影效应分量进行对比,发现:① 几种选点方案的预测均值与真实值相比都损失了部分细节成分,但都能大体恢复出区域内的阴影效应分量的真实值;② 当需推理点附近有监测数据时,则该位置的预测方差较小;反之,当距离最近的监测点较远时,预测方差较大;③ VI选点算法得到预测均值最接近真实值,且区域内方差整体较小。

图16 真实阴影效应
(a)GMIM选点及预测均值

(a)均匀随机选点及预测均值

(a)GMIM选点及预测均值

(a)VI选点及预测均值

(a)均匀随机选点及预测均值
为了对比不同场景下的算法性能,在使用RMSE和CRPS两种评价指标对上述5种场景的空间频谱推理性能进行了量化对比分析,如图22所示。仿真结果表明,在有限个可数点集范围内进行选点,GMIM空间选点算法与均匀随机选点相比,REM构建的RMSE可以降低1.23 dB,CRPS值降低0.64;对整个空间任意位置进行选点时,VI空间选点算法与均匀随机选点相比,REM构建的RMSE可以降低1.56 dB,CRPS值降低0.73。GMIM是针对有限个点的点集设计的优化方案,当待预测点不在GMIM算法研究的点集V内时,其性能不能得到明显提升,而VI选点方案对整个区域进行频谱推理时性能提升明显。

图22 不同选点算法的REM构建性能
综上,GMIM选点算法适用于可选点集和待预测点集为已知的离散点。在实际REM系统建设中,某一区域内设置频谱感知终端往往受到其他因素的限制(如建筑物的位置、设备网络接入等),仅能在有限个待选点中选择,结合系统需关注的待预测点,可以采用GMIM算法进行感知设备的选点规划。而VI选点算法能够大幅度提升整个区域内频谱推理的平均性能,但在实际系统建设实践中,VI算法得到选点位置可能会因为其他因素而无法设置感知节点。
5 结束语
本文提出了一种考虑环境异质性的TKL算法来处理空间频谱推理问题。主要思想是构造由参数表征的非线性单射变换来表示空间各向异性和非平稳性,结合GP建立TKGPR模型,利用梯度下降算法学习非线性映射和GP的参数,然后将训练好的模型用于空间频谱推理。受DKL启发的 TKL算法具有以下优点:首先,不同于DKL中DNN的非线性变换,构造的单射变换可以保持空间的拓扑结构。其次,在训练过程中不容易过拟合。结果表明,当群智感知设备的数量较多,局部空间内分布的采样数据密度较高时,空间频谱推理的性能得到显著提高。
在利用本文所提模型表征环境异构性的基础上,同样基于GP,提出了2种感知设备选点算法:基于贪婪算法的互信息最大化选点算法和基于变分推断的频谱感知设备空间选点算法。仿真表明,采用这2种选点算法与均匀随机设置监测点相比得到的空间频谱推理性能有所提高,其中VI算法推理的误差最小。2种算法都基于合理的数学分析和理论推导,有各自不同的应用场景,为REM构建中频谱监测设备空间选点问题提供了新的研究思路。
本文研究表明,GP方法适用于解决REM构建中的空间频谱推理问题。当前,将GP与深度学习算法相结合成为新的研究热点,将二者结合用于REM构建值得进一步深入研究。此外,本文重点围绕空间维度频谱数据进行分析,空时维度联合的频谱数据已经受到广泛关注,如何联合多维度的信息进行联合推理将成为本领域相关课题研究的重点。

