干扰条件下的星空协作认知网络鲁棒波束成形算法
王 薇,孙士勇,王子宁,杜 丹
(1.中国电子科技集团公司第五十四研究所,河北 石家庄 050081;2.南京邮电大学 通信与信息工程学院,江苏 南京 210003;3.陆军装备部驻石家庄地区第一军代室,河北 石家庄 050081)
0 引言
相比于地面移动通信系统,卫星通信具有覆盖范围广、通信容量大和不受地理条件限制等优点,能够为偏远地区用户提供传输服务,被认为是满足未来无线通信全球覆盖的关键手段之一,得到了国内外学者的广泛关注[1-3]。然而,卫星通信容易受到大气雨衰或者障碍物遮挡所引起的阴影效应的影响,无法保持与地面终端的视距连接,存在通信质量不稳定的问题[4]。为此,提出了协作通信技术,通过地面中继或无人机(Unmanned Aerial Vehicle,UAV)中继来提高卫星网络的传输质量[5]。相比于常见的地面中继,UAV具有成本低、易于部署和灵活性高等优点,在环境恶劣、地面基站无法触及的地区得到了广泛应用。因此,近年来基于UAV的星空协作网络备受人们的青睐[6-8]。文献[6]提出了一种多无人中继的星空协作网络架构,并推导了机会中继选择方案下的中断概率。在采用光电混合技术的星空协作网络中,文献[7]推导了遍历容量的表达式,提出了一种比例公平方案实现系统性能与服务公平性间的折中。文献[8]针对星空协作网络的上行传输场景,提出一种基于角度信息的空分多址方案以最大化系统的遍历和速率。
另一方面,考虑到星空协作网络中卫星和UAV网络都是资源受限的网络,存在着负载较低、时频带利用不充分的问题[9]。因此,通过波束成形(Beamforming,BF)和资源分配等方式实现主次网络频谱共享,有效提高混合网络整体频谱资源利用率的认知无线电技术应运而生[10],并已经在许多无线通信系统中得到了应用[11-14]。在Underlay的认知方式下,文献[11]提出了一种基于速率分割的BF方案,实现卫星和UAV网络的频谱共存和大规模接入。文献[12]针对次级用户信干噪比(Signal-to-Interference-plus-Noise Ratio,SINR)最大化问题,分别提出基于迭代以及基于迫零(Zero-Forcing,ZF)的BF方案,推导得到了BF权矢量的解析表达式。在现有文献中,Overlay认知方式下的研究大多集中在星地协作网络。文献[13]研究了卫星网络和地面网络协作传输的条件;文献[14]推导了非正交多址方案下星地认知网络的中断概率表达式。
然而,针对Overlay认知方式下的星空协作网络的研究甚少。并且,上述研究大多采用完美信道状态信息(Channel State Information,CSI)进行方案设计[11-14]。在实际通信系统中,由于终端移动性、反馈误差等原因,一般只能获得非完美CSI。受到上述文献的启发,本文针对UAV辅助的星空协作网络,提出一种基于功率最小化准则的鲁棒BF算法。考虑到UAV通过放大转发(Amplify-and-Forward,AF)协议转发卫星信号的同时,采用认知无线电(Cognitive Radio,CR)技术服务自身用户,并同时接收到多个干扰信号的情况,分别给出了各个用户的输出SINR表达式。然后,在假设所有用户CSI存在误差情况下,建立了以UAV发射功率最小化为目标函数、各个用户服务质量(Quality-of-Service,QoS)需求为约束的优化问题。针对此非凸问题,提出了一种基于ZF和半正定规划相结合的方法,求解得到BF权矢量。最后,仿真验证了所提方案的鲁棒性和有效性。
1 系统模型
基于Overlay方式的星空协作认知网络系统模型如图1所示。

图1 基于Overlay方式的星空协作认知网络系统模型
本文研究一个星空协作认知网络的下行传输场景,UAV网络作为次级网络采用Overlay的方式共享卫星主网络的频谱资源。在卫星主网络中,由于阴影效应的影响,静止轨道卫星与主用户(Primary User,PU)之间无法保持视距传输,位于卫星覆盖范围内的UAV作为中继节点,通过AF协议转发卫星信号,同时UAV将接收到L个干扰信号。此外,为了提高频谱效率,UAV网络作为次级网络在转发卫星信号的同时采用单播方案向K个次级用户(Secondary User,SU)传输信号。这里,假设PU和SU都配备单根天线,而UAV配备N根天线的均匀线阵(Uniform Linear Array,ULA),以获得较高的收发增益。
整个卫星通信过程可以分为2个阶段。在第1个阶段,卫星发送满足E[|s0(t)|2]=1的信号s0(t)到UAV,同时UAV会接收到L个干扰信号。通过无线信道后,UAV采用BF技术后接收到的信号可以表示为:
(1)
式中,v∈N×1为UAV的归一化接收BF权矢量,满足‖v‖2=1;Ps为卫星的发射功率;xl(t)为第l个干扰信号;gl∈N×1和Pl分别为第l个同频干扰到UAV的信道矢量和对应的干扰功率;nr(t)为均值为零的高斯白噪声向量,满足为噪声方差,IN为维度为N的单位矩阵。卫星到UAV的信道矢量可以表示为[15]:
(2)
式中,CL为路损,可以由下式计算得到:
(3)
式中,λ为波长;dR为卫星到UAV的距离。式(2)中,Gs为卫星的阵列增益,可以表示为:
(4)

(5)
式中,β=2π/λ为波数;d为阵列单元间距;θ为方位角。
在第2个阶段,UAV首先以增益G放大接收信号yr(t),增益G可以表示为[8]:
(6)
再通过发送BF传输给PU。为了进一步提高系统的频谱利用率,UAV同时向K个SU发送信号。因此,PU和第k个SU接收到的信号可以分别表示为:
(7)
(8)
式中,sk(t)(k=1,2,…,K)为发送给第k个SU的信号,满足E[|sk(t)|2]=1,wk∈N×1(k=0,1,…,K)为对应第k个SU的发送BF矢量;ni(t)(i∈{p,k})为均值为零、方差为的高斯白噪声;hk(k=0,1,…,K)为UAV到用户的信道矢量。在UAV通信场景中,UAV常常与地面终端建立视距链路进行传输,但是考虑到地面终端附近散射体的存在,地面终端在接收到直达链路信号的同时,也会接收到多径信号[16]。因此,根据文献[17],本文采用如下信道模型:
(9)
式中,Ln为散射径个数;ρ0,ρi分别为直达径和第i条散射的路损,其表达式与式(3)类似,并满足|ρ0|2比|ρi|2大5~10 dB;a(θ)为ULA的导向矢量,其表达式与式(5)相同。
根据式(7)和式(8),可以得到PU和第k个SU的输出SINR为:
(10)
(11)

2 鲁棒波束成形算法
在无人机通信系统中,上/下行链路的CSI通常由信道估计得到。由于本文考虑UAV悬停在空中的场景,因此,在一段时间内,可以认为UAV与卫星的位置是相对固定的。在这种情况下,对于上行链路,UAV可以直接利用信道估计获得CSI,与文献[15]类似,可以认为是准确的。但对于UAV下行链路,需要地面终端进行信道估计,并通过反馈信道发送给UAV。由于反馈信道容量受限以及地面终端的移动性,通常存在反馈误差。因此,与文献[18]类似,假设下行CSI是非准确的。本节将针对UAV下行链路存在的CSI不准确情况,提出了一种鲁棒BF算法,以实现信号的有效传输。
首先,考虑到UAV只能获得用户的非完美CSI,信道自相关矩阵可以表示为:
(12)

‖Δk‖≤εk,∀k。
(13)
其次,本文旨在满足所有用户QoS需求的同时,最小化UAV的发射功率。因此,考虑到非完美CSI,该优化问题在数学上可以表示为:
(14)
式中,γp,th,γk,th分别为PU和SU的QoS阈值;Pmax为卫星的最大发射功率。A0表示矩阵A半正定。

(15)
上述问题的目标函数随着Ps增大而增大,故上述问题达到最优解时,有Ps=Pmax。因此,式(15)可以重写为:
(16)
首先,对Hs和Gl进行特征值分解,得到:
(17)
(18)
式中,Σ为特征值矩阵;U为对应的特征矩阵。然后,构建如下零空间矩阵:
ZHv=0L×1,∀l,
(19)
式中,Z=(u1,u2,…,uL),ul为Ul的最大特征值对应的特征向量。根据ZF准则,权矢量v可以由下式计算得到:
(20)

(21)

(22)
其次,采用最差性能设计准则,约束C1可以重写为:
(23)
然后,对于约束C2,有:
(24)
将式(23)和式(24)代入式(21)中,并采用半正定松弛方法舍弃秩一约束C3,则有:
(25)
上述问题的目标函数和线性约束都是线性的,故式(25)为凸问题,可以通过CVX进行求解。
3 仿真验证
通过仿真验证了所提算法的有效性和鲁棒性,并引入非鲁棒算法和完美CSI算法进行比较。在所考虑的场景中,假设PU位于UAV-20°方向,3个SU分别位于0°,10°,30°方向。卫星最大发射功率为45 dBm,干扰发射功率为30 dBm。仿真中用到的其他参数如表1所示[11]。

表1 仿真参数
归一化BF权矢量w1的方向图如图2所示。可以看出,天线辐射方向图的最大振幅方向指向目标用户SU1,同时在非目标用户方向上产生较深的零陷。由此可见,所提BF算法能够在有效保证目标用户信号质量的同时,抑制对其他非目标用户的信号干扰,验证了所提BF算法的有效性。

图2 天线归一化辐射方向图
500次信道随机后,本文所提鲁棒方案和非鲁棒方案下不同用户SINR的分布直方图如图3和图4所示。由于存在多个SU并且它们的SINR性能图类似,则重点分析性能最差的SU。由图3可以看出,非鲁棒方案不能有效满足SU的QoS约束,有大约50%的SINR值低于目标阈值γk,th=1 dB。而鲁棒方案的SINR值都在阈值之上,并且主要集中在γk,th=1.65 dB处。类似的,图4中非鲁棒方案不能有效满足PU用户的QoS约束,而鲁棒方案在信道存在误差的情况下,也能充分满足PU的QoS约束,这说明本文所提方案具有良好的鲁棒性和有效性。

图3 SU SINR分布直方图

图4 PU SINR分布直方图
不同方案下总传输功率和用户SINR的关系如图5和图6所示。可以看出,随着QoS需求的不断增大,系统所需的总放射功率呈非线性增长。这是因为随着QoS需求不断增大,各个用户间的干扰将不断增大,导致UAV需要更大的发射功率以满足通信需求。此外,随着误差自相关矩阵Frobenius范数界εk的增大,所需的功率也不断增大。这是因为随着εk的增大,信道估计越不准确,为了保证在所有CSI条件下都能满足用户的通信需求,需要更加严格的方案设计,即基站发送更大的功率以满足最差情况下的性能。
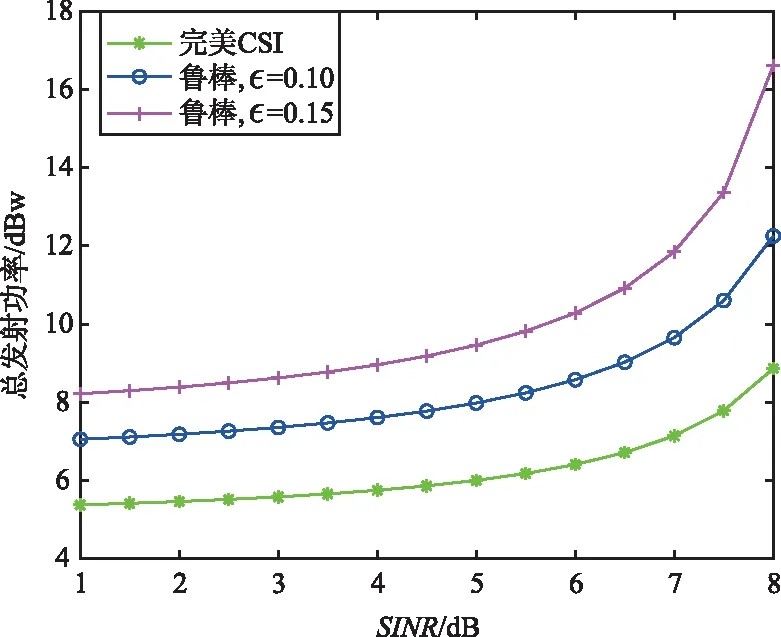
图5 PU SINR与总发射功率的关系

图6 SU SINR与总发射功率的关系
4 结束语
本文研究了星空协作认知网络的下行传输问题。针对UAV次级网络采用Overlay方式转发卫星信号并服务自己网络用户的同时,受到多个干扰的场景,分别给出了各种用户的输出SINR表达式。然后,利用非完美CSI,建立了以UAV发送功率最小化为目标,用户QoS需求为约束的优化问题。针对此非凸问题,采用ZF和半正定规划相结合的求解方法得到BF权矢量。最后,仿真结果表明所提算法的有效性和鲁棒性。

