基于导航技术和WebGIS技术构建的校园导航平台

樊 浩，徐明伟

(1安徽广播电视大学，合肥 230022； 2合肥滨湖职业技术学院，合肥 230601)

0 引言

随着IT技术的飞速发展，高校校园作为产学研的前沿基地，校园管理的信息化和数字化将成为校园建设发展的必然趋势。目前国内上千所高职院校的校园规模越来越大，但校园软体建设发展相对缓慢，校园信息平台仍采用传统的C/S模式，校园信息管理仍多以人工为主[1]，这使得构建一个智能的电子校园导航平台显得非常必要和迫切。

智能校园导航平台能辅助获取到最新的校园环境信息、实体建筑信息、地上线路图、地下电网图等。通过智能选择目的地和源地址，可以辅助快速选择最佳的导航路径，并且以三维图的形式展示给用户[2]。同时可以便捷地采集校园信息，尤其是环境信息，便于校园信息管理和相关校园建设的辅助决策[3]。

本文基于导航技术及WebGIS(万维网地理信息系统)技术构建校园导航平台，以实现校园建设的信息化、数字化、智能化。该平台以WebGIS和SuperMap iObjects组件为技术架构，将SuperMap iObjects技术与OLE(对象连接嵌入)和SDE(空间数据引擎)结合，通过组件的方式提供服务，实现B/S技术架构，不需要下载客户端，支持终端用户在浏览器上使用该导航平台。此外，对SuperMap iObjects组件技术进行优化封装，以提升平台空间的数据处理能力。同时对Dijkstra算法从搜索方式和地理信息存储方式两个方面进行优化。

通过该平台可以实现：1)终端用户可以在平台上对地图物体进行任意缩放及漫游控制，对于选取的区域进行三维全仿真展示；2)进行信息的采集、查询、检索，并与校园其他系统集成，同时能够在同一维度查阅相关信息；3)纳入高校人员信息，辅助管理者进行人员信息管理等。

1 技术架构

1.1 技术框架

传统技术中被采用的地理数据系统采用的为地理信息元数据，主要描述地理数据的内容、质量、状态及相关特征，一般适用于专业领域[4]。本系统基于WebGIS技术，通过GIS系统采集多源的空间地理数据，由专业系统对封装数据进行预处理、分析、转化等，向终端用户提供地理数据服务。

传统的互联网系统中一般采用C/S模式，由于C/C++/.NET/DEPHI等开发语言同时适应于客户端和服务端，且之前的应用体量小，所以C/S优势明显[5]。但随着IT技术的发展及用户体量的迅猛增加，使C/S维护成本高、开发成本高、不灵活等弊端逐步显现。随着Web 2.0的广泛使用以及前后端开发语言的发展，B/S成为中小型平台的常用解决方案[6]。本文所述平台采用B/S开发模式，利用WebGIS技术和组件技术构成服务端框架，通过互联网提供地理信息服务。

本平台在服务端结合SuperMap iObjects组件，将WebGIS核心技术封装在自定义iObjects组件中，对外提供地理数据采集、预处理、处理、数据转换、分析及统计服务等。

1.2 技术分析及优化

本文涉及的主要技术包括B/S模式、WebGIS技术、导航技术、SuperMap iObjects组件技术。

B/S模式以Web服务器为核心，用户通过万维网服务工具，一般采用浏览器访问Web服务器，服务请求和响应都在网页上完成。

WebGIS技术是GIS在Web框架下的应用，GIS地理信息系统专门负责对多源多方式的地理空间数据进行采集，并利用专门组件模块完成数据清洗，包括数据类型转换、数据结构映射、数据存储等[7]。然后，利用GIS核心模块，对数据进行处理，并且展示到Web客户端。此外，还可结合海量的地理数据信息，对相关数据的应用部门提供数据分析和统计服务。

在网络应用开发技术中传统的是采用CGI通用网关接口，随着用户体量变大且应用越来越复杂，CGI脚本编写也越来越复杂，严重制约着应用的发展，且CGI每次升级都需要重启，对应用直接产生影响[8]。插件Plug-in技术成为CGI技术的扩充，通过动态链接库加载，节省内存，提升访问效率。本文采用SuperMap iObjects组件构建GIS系统，每个GIS模块通过组件对外提供服务，组件的方式灵活、易扩展，组件技术完美契合B/S模式架构[9]。

SuperMap iObjects技术是基于三维一体化、高性能、跨平台的大型组件式GIS开发平台，功能完备、开发便捷，易于构建通用GIS平台以及基于地理空间信息的行业应用系统[10]。SuperMap iObjects技术采用面向对象的架构，提供应用程序之间的对象访问，其功能不受限于平台和操作系统，可大大提高软件开发效率和利用效率[11]。

iObjects组件按照图层的方式组织整个物理空间，不同图层代表不同的物理属性，譬如建筑物为一个图层，道路为一个图层等等。这里图层为矢量图层，基于坐标数据，用于展示物理特性，如图1所示。

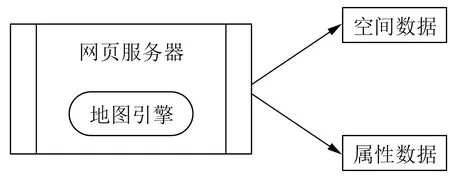
图1 Web结构示意图

本文重点研究iObjects组件功能实现和导航技术最短路径的问题。其中iObjects组件通过对外提供服务实现WebGIS系统的图像处理功能。采用SupperMap iOBjects组件来实现WebGIS技术，通过封装已有的接口及方法实现图像处理、二维路径计算、数据搜索、数据缓存、路径对比、数据缓存等功能。通过SuperMap iObjects Java实现地图预处理及地图匹配。

关键控件/接口包括Workspace类和MapControl类、MapMatchParameter类、PathAnalyst类、SSCDataEnvironment类和GPSData类。

核心算法包括MapMatchParameter.setTime()方法、SSCDataEnvironment.connectData()方法，以及用于路径分析和计算的PathAnalyst.setSSCEnvironment()方法、PathAnalyst.mapMatch()方法。

地形边缘平滑处理功能主要解决不同分辨率地形叠加边缘处断崖问题。关键控件和接口主要包括：Workspace类、Datasource类、DatasetGrid类和ConversionAnalystParameter类、Recordset类、DissolveParameter类和Generalization类；方法包括Generalization.dissolve()方法、Recordset.getGeometry()方法、RasterClip.clip()方法、BufferAnalyst.createBuffer()方法、VectorClip.clipDatasetVector()方法和ConversionAnalyst.rasterToVector()方法。

2 Dijkstra算法

导航技术基于数学图论理论获取最短路径，将地图中的道路和建筑等抽象为点与点的关系，即网格关系，通过研究点与点之间的关系，计算出最优解，进而得到最优的路径。

在研究导航Dijkstra算法的优化之前，有必要先介绍一下涉及到的概率图、图论、网格及最小路径问题。

图论中的图是指所参照的事物之间的相互关系，如果以点表示具体事物，事物与事物之间的关系以线表示，则地图上所有点及点之间联系的集合，即为将研究的图。以G表示图，通常为一个有序二元组{V，E}，即G=(V，E)，其中V={v_1，v_2，…，v_n}为有序非空集合，V中元素称之为顶点，而V称之为G的顶点集合。E为V中不同元素之间的非有序对偶(即为(v_i，v_j)其中v_i≠v_j，这些非有序对偶称之为边，而E称之为G的边集。网格为在图的基础上在每条边上加上权值，即为w_i，权重可以表示价格、流量或者时间等，网格不仅仅可以体现几何中的事物，也可将实体事物抽象为网格，网格被表示为N=(V，A，W)，由G图及其权重构成，其中G=(V，A)，W={w(v_i，v_j)}，(v_i，v_j)∈A。网格中节点和边在不同事物中可以表示不同的含义。在WebGIS系统中由于GIS都是以实际物体作为基础，所以这里表示图中事物的坐标，而边值权重要具体问题具体分析，可表示长度、时间、费用等元素，在本系统中最小路径算法计算权重值时计算的是实际点距的长度。

所谓最小路径问题，是指在一个网格中，其中一个顶点作为源点，一个顶点作为终点，网络权值取相邻两点的长度值，寻求任意两点v_i，v_j之间的最小路径长度。

Dijkstra算法提出了在有向的图中按照路径递增的顺序计算最短路径的方法。Dijkstra算法的基本思想是利用源点v，找到与之相邻的最小路径的点v_i，然后再以v_i为源点找到与其相邻的最小路径的点v_j，依次类推直到找到终点v_k，从而形成集合w={v，v_i，v_j，…，v_k}，则为最小路径点集合。具体算法：

1)假设抽象带权重的有向图为邻接矩阵Square，其中Square[I，j]表示(v_i，v_j)两顶点边上的权值。若(v_i，v_j)不存在，则Square[I，j]表示为∞。其中S表示从v点出发最短路径的顶点集合。集合S最初始的状态为空集，从v点出发到达各个顶点v_的i最短路径权值长度表示为dist[i]=Square[v_0，i]，(v_i∈v)，其中v_0为起点序号。

2)选择顶点v_j，并得到dist[j]=Min{dist[i]|v_i=V-S}，其中v_j表示从v_0出发寻求最短路径的路线的终点，其中S=S∪j。

3)寻求从V出发到集合V-S的最短路径中的顶点v_k，若存在dist[j]+Square[j，k]

4)重复2)、3)步骤n-1次，得到从v到其他顶点长度为递增的顺序。

5)Dijkstra算法中按照前述步骤，每次以当前顶点为源点，依次找出到各点的最小路径长度，经过复杂度O(n^2)计算，得出从v点出发到达有序图所有终点的最小路径集合S。

本文的研究方向是在导航技术中寻找最短路径，抽象的图集为有向带权图，所以可利用不规则图形限制搜索范围，范围内的顶点在目标有向路径上，进行Dijkstra计算时只需考虑搜索范围内的顶点。本文采用椭圆不规则图形限定搜索范围。

通过给定起始和终止节点M、N，以此两点构造椭圆区域，在此椭圆区域内的顶点纳入计算节点，否则不予不考虑。假定D=|MN|，其中D表示M、N两点的欧氏距离，用于限制其他节点是否纳入计算。

构建椭圆时，以M、N为椭圆的两个焦点，D=|MN|为椭圆的焦距，R为椭圆的长轴，并设定R=τD，其中τ取正实数，一般取值为1.25。由于椭圆内的点满足：|SM|+|SN|<|MN|，所有此部分的顶点集S均纳入计算范围，而|XM|+|XN|≥|MN|为椭圆外的顶点，不纳入计算范围。

按照前述方式对Dijkstra算法进行过滤，选择顶点，若此次椭圆范围内未找到最佳路径，按照一定比例扩大椭圆范围，直至选择到最佳的路径为止。

应用Dijkstra算法进行导航路径规划的效果图如图2所示，优化后得到的结果如图3所示。执行效率对比见表1，对比原始算法，本文的改进算法在导航路径规划中具有收敛速度快，准确率高，并且能以大的概率收敛获得全局最优解，尤其适合复杂环境。

图2 基于Dijkstra算法路径规划图

图3 基于优化Dijkstra算法的规划路径

表1 改进Dijkstra算法与原始算法导航时间对比表

3 结论

本文所设计的导航平台对于高校构建智能管理导航平台有参考意义。首先利用WebGIS技术及SuperMap iObjects Java组件技术，构建了智能导航平台框架。其次研究了导航最小路径Dijkstra算法的优化路径，并结合校园导航平台的特点，从搜索范围及数据存储结构方面进行了优化，提升了导航功能的选址效率。