跨逆断层隧道应力影响因素的数值模拟分析

张云飞，李席盈

(广东省地质局第三地质大队，广东 韶关 512000)

0 引言

隧道等地下工程穿越断层或接近断层的现象越来越普遍，而且地震活动不断增强，导致断层活化引起地下工程被破坏的情况越来越频繁，很多学者开始进行跨断层隧道的研究。林克昌等[1]利用有限元软件ABAQUS建立断层错动三维有限元计算模型。在此基础上，以走滑断层为例对比分析在断层宽度逐渐增大的过程中，跨断层岩体隧道的错动反应特性。何川等[2]采用振动台模型试验及数值计算的方法，研究围岩与隧道结构的加速度响应特性、地层变形及衬砌结构内力分布规律等。赵颖等[3]研究了正断层位错作用下城市地铁隧道的抗震薄弱部位，为地铁隧道工程的抗震设计及地震安全性评价工作提供依据。黄芸等[4]在缺乏有效的理论预测模型的情况下，基于不排水条件下上覆土体的变形机理，对正断层错动引起的地铁隧道变形破坏，找出了地铁隧道变形的计算方法。信春雷等[5]通过分析围岩与隧道结构的地震加速度响应、震动应变响应以及隧道结构的震后破坏形态，以无抗减震措施和无断层为例，对在直立与倾斜走滑断层处设置的套管式可变形抗减震措施进行了系统研究。张旭[6]针对某隧道二衬施工中存在的缺陷进行了原因分析，介绍了先进工装和施工工艺，保证二衬混凝土施作质量和安全。熊田芳等[7]研究西安地铁二号线穿越断层的隧道，采用1∶50的几何相似比进行了物理模型试验，开展了断层活动下隧道正交穿越断层时围岩和衬砌相互作用的机理研究。

国内外跨断层隧道的研究主要侧重在3个大的方面：断层特性、围岩性质、隧道的性质。本次数值分析主要在定量的基础上探究影响跨断层隧道应力的主要因素，为学者以后进行相关的研究提供参考。

1 模型设计分析

本文选择影响跨断层隧道稳定性的4个主要因素进行数值模拟分析，4个主要因素分别为断层倾角、断层破碎带宽度、围岩等级和衬砌级别，每个因素选取3个参数(水平)采用正交试验的方法进行设计。

1.1 模型的尺寸效应

有关文献的研究指出考虑到尺寸效应[8]，地下结构有限元计算模型的围岩范围应设定为3～5倍洞径[9]，超过5倍之后人工边界对于计算结果影响甚微。文中忽略了埋深对围岩的影响，并且认为围岩是不含结构面的均质、连续、各向同性的块体。为了尽量减少尺寸效应的影响，本文选取的围岩范围为隧道洞径的7倍，隧道—围岩的相互作用通过摩擦接触面来考虑，为简化计算并结合实际的受力关系，将一衬和二衬简化为一体，不考虑两者的相互作用关系。

1.2 影响因素的选取

每个影响因素均选取3个水平，断层特性中选取断层倾角15°、30°、45°和断层破碎带宽度0 m、20 m、40 m，围岩性质选取Ⅱ、Ⅲ、Ⅳ级围岩，隧道衬砌选用C20、C30、C40级混凝土。

1.3 正交表的选择

正交试验设计是利用正交表来安排与分析多因素试验的一种设计方法。它是在试验因素全部水平组合中，挑选部分有代表性的水平组合进行试验。通过对这部分试验结果的分析，了解全面试验的情况，在正交试验里面找出最优的水平组合。跨断层隧道稳定性试验方案见表1。

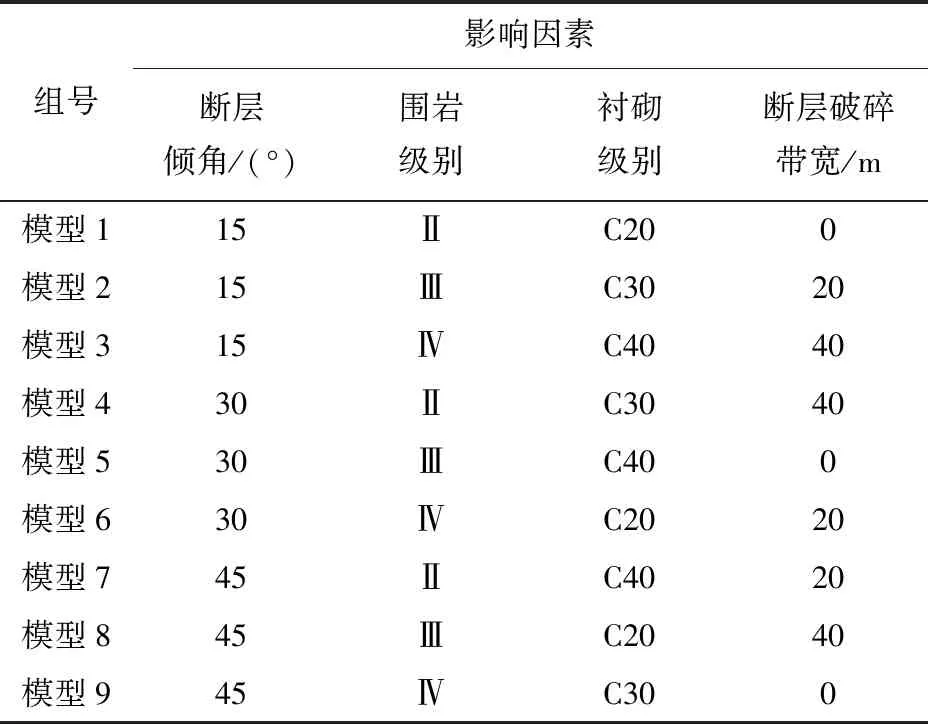
表1 逆断层隧道的正交试验设计

2 数值模拟分析

与模型试验相比，数值模拟能较好地模拟复杂的施工工艺、荷载的作用方式及时间效应等，能研究工程的受力全过程，从弹性到塑性，直到破坏，不仅可以研究工程的正常受力状态，还可以研究工程的极限荷载及破坏形态。而MIDAS-GTS数值模拟软件具有十分丰富的单元库和材料模型库，拥有适用于多数工程材料的本构关系。本文采用数值模拟软件MIDAS-GTS对跨断层隧道进行研究。

2.1 模型尺寸的选取

基于有限元和力学的基本原理，参考实际工程的地质工况和设计，对隧道模型进行优化处理。模型选取的隧道形状简化为圆形，其外径为10 m，壁厚为40 cm，衬砌也简化为素混凝土。

实际工程中隧道的长度有数千米，为了获得合理计算长度的隧道模型，进行了多次的试算，在计算的过程中，逐渐增大计算模型的长度，发现在断层附近的一定范围内，衬砌的反应不再发生变化或者变化很小，此长度确定为合理长度。建模尺寸为上盘的下表面长度，尺寸被控制为75 m，两侧采用一致的布置，如图1所示。

2.2 围岩模型的选取

岩土本构模型[10]多达数百种，大体上分为：弹性模型、弹塑性模型和黏弹塑性模型等几类。实际工程中岩土体常有比较复杂的应力—应变特性，同时受应力历史、应力路径以及岩土的状态、结构、组成和温度等不同因素的影响。因此，为了反映岩土体真实的力学性状，必须建立较为复杂的本构模型。但在实际工程应用中，在满足一定精度的条件下，要求简单实用，满足分析即可。选取围岩用的经典的摩尔库伦本构模型。

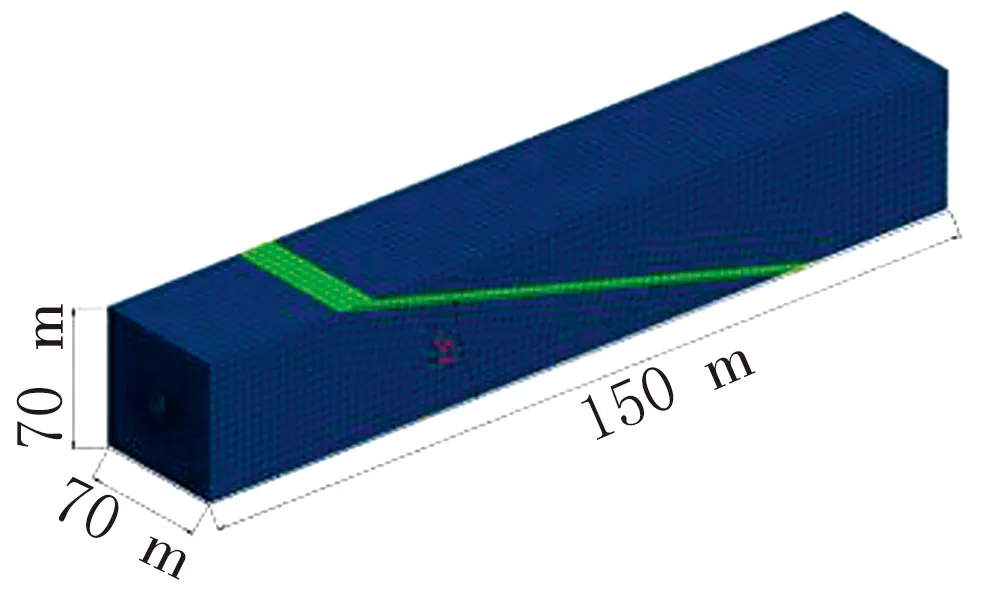
图1 跨断层隧道计算模型

2.3 断层面模型的选取

在地质力学有限元分析中，关于断层的处理方法主要有两类：一是将断层处理为特殊的连续介质体，即弱化带模型；二是将断层作为非连续特性的位错面来模拟，主要有接触模型、劈节点模型和块体模型。

断层面采用MIDAS-GTS提供的接触面来模拟，综合运用介质弱化模型和接触模型两种方法来模拟断层。接触面单元原理示意图如图2所示，恰当地对图中各参数进行设置则能较好地模拟断层的非线性滑移和分离，根据接触面两侧岩土的材料参数，综合判断可以得出各参数值见表2。图2中S指滑块，TS指抗拉强度，SS指抗剪强度，D指膨胀角，KS指剪切刚度，Kn指法向刚度。

图2 接触面原理示意图

表2 接触面参数

2.4 数值模拟参数的选择

数值模拟的各种材料的参数见表3。

表3 各种材料参数

3 数值模拟结果分析

隧围岩采用MC本构模型，衬砌采用混凝土损伤本构模型中的线弹性本构关系。单元类型均采用实体单元，隧道—围岩的相互作用通过摩擦接触面来考虑，结合实际受力情况简化计算，将衬砌视为素混凝土且只有一衬，隧道的截面形心和围岩横截面重合。加载时考虑初始应力即重力的影响，每0.05 m加载1次，最大加载量为0.5 m。跨断层隧道受到的应力采用极差分析方法，确定影响隧道应力的主要因素。

3.1 隧道的应力反应

模型1隧道沿x轴方向的应力值，负值代表压应力，正值代表拉应力，随着断层错距的增大，压应力拉应力数值均变大，如图3所示。隧道沿y轴和z轴的最大应力变化与x轴的变化规律一致。在断层破碎带边缘位置处，拱顶首先出现最大位移，拱腰对称地出现较小位移。随着接近断层破碎带中心，拱顶最大位移的范围逐渐扩大，最后对称波及到拱腰。

3.2 逆断层影响因素分析

逆断层影响因素极差分析结果见表4，因素A代表断层倾角、因素B代表围岩级别、因素C代表衬砌级别、因素D代表断层破碎带宽度。K1、K2、K3分别表示各因素3个水平对应指标值的平均值，极差R表示K1、K2、K3中最大值与最小值的差值。极差R代表因素的重要程度，R值越大表示该影响因素越重要。

(a)加载量0.1 m时的隧道应力

(b)加载量0.3 m时的应力图3 15°断层倾角C20衬砌隧道沿x轴方向应力

因素A的拉应力极差为0.324 MPa，是压应力极差0.300 MPa的1.08倍，则因素A即断层倾角对隧道拉压应力影响较大，而隧道混凝土抗拉能力弱，则因素A是次要因素。

因素B的压应力极差是拉应力极差的近9.53倍，远大于对应拉应力的极差，说明因素B即围岩级别对于隧道的压应力影响较大，因而因素B是主要因素。

因素C的压应力极差是拉应力极差的2.41倍，对于跨逆断层隧道的受力也是有利的，则因素C即衬砌级别对隧道的影响是稍次要因素。

因素D的拉应力极差0.634 MPa是压应力极差0.087 MPa的7.29倍，对隧道的拉应力影响大于压应力，即断层破碎带宽度是影响隧道的主要因素。

由前述分析可知因素B围岩级别、因素D断层破碎带宽度，对隧道的拉压应力的影响最大，而因素A断层倾角、因素C衬砌级别次之。对于拉压应力这两个物理力学参数指标，各自影响因素的主次排序见表5。

表4 跨逆断层隧道影响因素结果极差分析

表5 跨逆断层各因素对各指标影响的主次排序

4 结语

针对跨越断层破碎带的隧道，开展了岩体隧道工程稳定性影响的数值模拟研究，并得到的主要结论：

1)本文用正交试验的方法，对影响跨断层隧道的4个因素：断层倾角、围岩级别、衬砌级别和断层破碎带宽度，设计了9种试验方案，并对试验采用数值分析软件MIDAS-GTS进行模拟。

2)不同位错量下隧道在各个方向受到的拉压应力规律相似，压应力是拉应力的2倍左右，在一定范围内均随着位错量增大而呈现线性增长。

3)用极差分析法对影响隧道的4个因素进行分析，表明影响跨断层隧道拉应力的主要因素为断层破碎带宽度；影响跨断层隧道压应力的主要因素为围岩级别。

4)地铁隧道、铁路建设等在穿越断层时，应选择破碎带宽度较小且围岩级别较好的地段。