正则性方法的内涵与理解

曹志杰

(三峡大学理学院 湖北宜昌 443002)

微分方程解的正则性在数学研究中非常重要，此外还有其他对象的正则性。研究发现，不同的数学对象，有不同的正则化过程和正则性要求。这给数学研究者，尤其是初级研究者带来很大的理解障碍。基于这种状况，考察一般正则性与正则化的基本内涵，给一些不同的正则性和正则化的理解提供一种“范式”是必要的。该文正是基于这种考虑，试图为较为容易地理解和把握种类繁多的正则性和正则化现象，介绍一种思路。

1 正则性概述

研究解的正则性是微分方程求解分析中非常重要的一个方面。文献[1]的第四章第六节详细说明了数学家对微分方程求解的正则性分析过程：从古典导数到广义导数，且引出广义函数从而将方程的求解范围逐步扩大以得到解的表达式，接着分析傅里叶变换的逆对应的空间变化等内容，为将由广义导数表达的解回到古典导数上打下基础。其实整个过程，就是先用某种方式将解表达出来，然后分析这样做时出现的问题并加入条件将问题解决。微分方程解的正则性讨论在硕、博士毕业论文中也屡见不鲜，比如：文献[2]详细讨论了Landau-Lifshitz 方程与Maxwell 方程在自旋累积效应下耦合系统解的部分正则性等性质及三维A带自旋扩散的Landau-Lifshitz-Maxwell系统的部分正则性；文献[3]利用解析半群理论、分数幂理论、不动点定理研究了两类具有非局部条件的中立型发展方程解的存在性与正则性问题。文献[4]证明在一定条件下不可压三维Navier-Stokes 方程的弱解u是正则的；文献[5-7]分别研究了三维广义的MHD系统和Hall-MHD系统的正则性规则，Navier-Stokes方程的局部正则性条件，和三维MHD-α型模型全局吸引子的正则性。

数学文献中遇到的正则，涵义往往有很大差异，如函数正则化方法、某测度是正则的、偏微分方程解的正则性估计等表达，还有，如正则性公理（也叫基础公理，是Zermelo-Fraenhel 集合论中的公理之一）、正则表达式（这是一种可以用于模式匹配和替换的工具，可以让用户通过使用一系列的特殊字符构建匹配模式，然后把匹配模式与待比较字符串或文件进行比较，根据比较对象中是否包含匹配模式，执行相应的程序）等。语义上，以上出现的“正则”各对应正则（regular），或正则性（regularity），或正则化（regularize）中的某一种或几种。在不同的数学学科背景中，这些“正则”的意义相差甚远，初学者对这些差异会感到极大的困惑。这个困惑的程度，比另一个常见的数学名词——齐次性，引起的要严重一些。毕竟，诸如（非）齐次线性方程组、齐次微分方程、齐次多项式（函数）等，这些“齐次”的含义虽然不同，但其定义很清晰，理解起来一般不会有难度。

由此可知，正则现象（指某对象的正则性和正则化）与某种规则相连。正则化，顾名思义，就是根据某规则，按照（某种）方式行事，这个过程中要求的对象的性质，就称为正则性。粗略来讲，正则就是在实际应用中向某个规则靠拢，以此解决仅靠规则解决不了的“棘手”问题以及由此而产生的一系列相关问题：譬如函数正则化方法，是用光滑函数逼近一般函数（其光滑程度不满足实际需要）的方法，就是函数向光滑函数靠拢之意，二者达到一定的接近程度，就可用光滑函数的方法来解决一般函数的问题；某测度是正则的，按照定义指的是对集族中的任一集合（对测度而言，是非常“难测”的），都可找到一个“可测”的集合，使后者包含前者，并且二者的“测度”是相等的，这可理解为集族中任一集合的某度量都向某一测度靠拢，因而得到集族的一个测度。

对方程解的正则性进行估计是求解偏微分方程时的一个重要问题。事实上，假设解是存在的，只需要再证明某种先验估计，解的存在性就得到证明。具体地，对于一个方程Lu=f，其中L是一个古典导数算子，如，物理上要求方程的解在最低二次可导函数空间X中，但要在这个空间X中求得方程的解，是困难的。这个空间上的算子欠缺“好”的性质，如自反性、严格凸及列紧性等。为此，数学家引入了“弱导数”及“广义函数的导数”等概念，将古典微分算子L“弱化”为弱算子LC。这个弱算子是哪怕对于基本的可测函数，也可以对它求导（弱导数），而且这个弱导数算子对应一个较好的空间（Sobolev 空间等），数学上这些空间中的算子具有非常丰富的性质。由此人们就易于得到方程LCu=f的解，但这是“弱解”——弱算子LC对应的解。回到原方程，我们发现，弱解所在的空间不具有相应的物理意义，为解决实际问题，我们还得回到古典导数意义下的函数空间，就是要再回到前述空间X上。这个弱解是否能与如何“回到”古典导数空间X中，就是原方程解的正则性估计问题。总结整个过程，就是为了在X中求得方程的解，我们退而求其次，选择一个更大（条件更宽松，以致原本不可以求导的函数都有导数）的函数空间，自然在其中较易得到原方程的解（是弱解），然后在对其“正则化”，即寻找条件，使得弱解能“回到”原空间X中。循着这个模式，我们就可以大体把握偏微分方程理论对具体某方程求解的过程了。

其余部分安排如下：第2 部分从正则性（化）的角度分析黎曼积分定义，给这个过程一个正则化的理解；第3部分结合卷积的性质，利用磨光技术，考察将一般函数磨光为光滑函数的过程，这也是一种正则化。最后给出该文的结论。

2 黎曼积分过程

积分就是为解决面积问题而提出的。求平面图形的面积，我们自然求助于规则图形的面积公式，那么，对不规则图形，如何求面积？

黎曼积分（就是一般微积分教材中的定积分）给出了基于正则性（化）思想的处理办法——在平面图形的曲边逐点连续时用求规则图形面积的公式得到任意不规则图形面积的一种方法。

回顾定积分概念的引入。任给一个平面图形，如何得到它的精确面积？

这里该文考虑用已有的面积公式，即希望能使用某已知求面积公式。用哪一个公式？如何用那个公式求出这种图形的精确面积？这两个问题都很关键。应当注意到，整块平面的面积等于将它分割成各部分后各部分面积相加的结果。因此，下面该文的考虑思路是，首先将这一平面图形规则的分割成几大块，针对其中的某一块，在某个坐标系下将其再分割成与某坐标轴平行的、仅有一边是曲线的图形；下一步是继续分割，让每一个这样的图形越来越窄，及每一个的曲线边的长度越来越小。这样的操作一直下去，直到这些不规则的窄长的图形几乎可视为规则的矩形，就可以用公式计算出这样的每一个图形的面积，然后再把这些部分的面积加起来，就可以求得整个不规则图形的面积。

该过程中就使用了正则性方法，即求解时确定用某一目标公式，然后就向这个公式靠拢，考虑在何种情况下可以正当合理地使用这个公式。这个过程也能使研究者更深刻地理解函数在某一点连续定义的深度。下文是具体过程。

可先粗略地将任意平面划分为I、II、III、IV四部分（见图1），每个部分就相对规整一些。一般而言，我们考虑形如V 的图形（见图2）（称为曲边梯形，假设其中的曲边所在曲线的方程已知，记为y=f(x)；而该曲边梯形若除去其下方一个同底的矩形，就可对应前述四部分中的某一个）的面积。对平面图形来说，面积等于划分后它的全部各部分面积之和，因此，前述任意图形的面积就等于划分后的四部分面积之和。基于此，对曲边梯形V 有规律地划分，使得到的每一小部分都是一个窄的曲边梯形。小曲边梯形越来越像矩形，但毕竟不是，因此还不能用矩形的面积公式。

图1 任意平面图形的分割

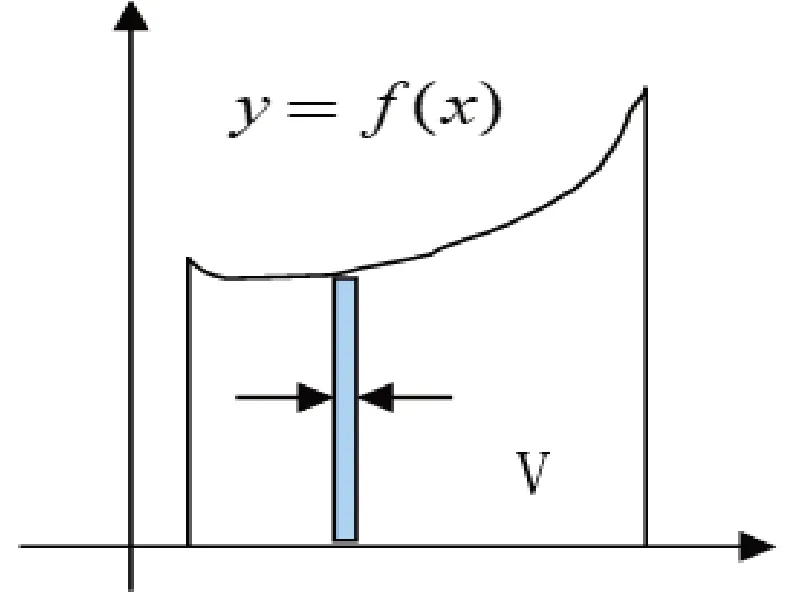
图2 曲边梯形的细分

小差距总是存在，总是不能实至名归的用矩形面积公式来求阴影图形的面积，怎么才能实现这个目标呢？根据函数在一点x0处连续的概念，有

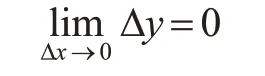
其中Δx=x-x0，Δy=f(x)-f(x0)，考虑到Δx→0 并不表示Δx=0，于是就有一个宽为Δx，长为f(x0)的确定的矩形，它的面积当然就是f(x0)Δx。当函数y=f(x)在研究区间内每一点处都连续时，就可以给出这样的结论：所谓曲边梯形的面积实际上等于若干矩形面积之和，这正是黎曼和。这个过程，就是在矩形面积公式的指引下，逐步将不规则图形的面积用这个公式处理的过程，实际是一个正则化的过程：将不规则的图形的面积用规则图形面积的计算公式求得，过程中涉及到平面面积的整体等于部分和属性，及对曲线（曲边梯形之曲边）在研究范围内每一点的连续性等性质，这些也可以理解为曲边梯形面积求解过程中涉及的“正则性”。以上是一维空间的情况，推广开来，多维也有类似结论，而且，随着空间维度的增加，涉及的正则性的研究会越来越复杂。

为了能用矩形的面积公式，要求这个小部分是一个精确的矩形。这个过程如何向矩形靠拢呢？对曲边提一个要求，即其上每一点处曲线都是连续的，这就能做到当两长边的距离趋于零时两长边的差距也趋于零，从而每个窄的曲边梯形就做成一个矩形，这就是一个正则化的过程。

黎曼积分的这个过程中要求的曲边上每一点都是连续的在物理场景中是一个非常苛刻的条件，这也是后来勒贝格积分（另外一种源于正则化思想求不规则图形面积的处理方式）得以替代并在用途上远远超越黎曼积分的一个原因。

3 一般函数的磨光

在函数的使用过程中，一定的光滑性是必需的。但在实际问题中，函数的光滑性往往达不到使用的要求，因而要增加函数光滑性。对应的操作，就是对函数的磨光。

函数的光滑性也称为函数的正则性。光滑性在函数的使用过程中至为重要，因而对一般的函数会尽量使其具有光滑性。这个方法称为对函数磨光。这也是一个正则化的过程，将一般函数“磨成”光滑函数。

考虑到卷积的性质：“若f与g中之一是可微的，则其卷积也是可微的，且其阶相同”，那么对于一般的研究对象，只要找一个光滑函数，二者一做卷积，一般函数就磨成光滑的了。随后用磨成的光滑函数代替原初的研究对象，最后用卷积的逆过程回归到原研究对象，这里面的问题可归结为正则化的问题。

4 结论

微分的逆运算是积分，那么微分方程的解就是积分的结果或是一种积分形式。而微分方程，无论常微分方程还是偏微分方程，涉及的微分一般都是古典导数意义下的。在古典导数意义下，即使初等函数，求积分问题也没有完全解决，那么研究者是如何研究一般由古典导数意义给出的微分方程的呢？为此，人们引入了广义导数，它是建立在积分过程之中：利用一般分部积分过程，定义弱导数；又根据函数序列在可积空间中的收敛，可得强导数的概念。这两个定义是可以互相推出的，也就是等价的。有了广义导数，对微分方程的研究就转移到了可积空间，如Sobolev空间、Besov空间等，利用这些空间的性质，可分析对应微分方程的解的各种形态。鉴于一般微分方程的复杂性，一般是将空间范围扩大，以找到它的解，然后在回到方程所在的恰当的空间。这个回到恰当空间的过程，就是一个研究正则性的过程。什么是正则性？为什么可直接求解的微分方程无正则性研究？就是因为对可求解的方程而言，无需再回到原空间中的缘故。这里正则性要研究的内容就是由广义导数进行的微分方程解的分析与方程真正的解之间有何关联、差别在哪里、还有哪些未考虑到的内容等。

通过考察黎曼积分过程和一般函数的磨光经历及微分方程的求解策略，阐释数学问题处理过程中常用的正则性（化）思想。具体地讲，就是在规则严格不允许使用时，如何使研究对象巧妙地运用该规则，并处理随之而来的一系列问题，最终回到原问题上去的过程。读者朋友见到正则现象时，若能够分辨具体问题中要适用的规则，和规则的要求不被满足的情况，积极地联系上下文，确定“正则化”过程，初步理解涉及的正则概念，该文的目标就实现了。

另外，正则也作为奇异的反义出现，如由局部可积函数构成的所谓正则广义函数和不是由局部可积函数构成的奇异广义函数。类似的情况很多，这里就不一一详举，这样的例子往往含义是清晰的。对如解的正则性这类正则性方法的使用，读者可依据文中提到的正则内涵，结合正则出现的具体环境去考虑其涵义。