基于组合神经网络的钨极氩弧焊环境负荷预测

蒋伟琪，黄海鸿，刘赟，李磊，刘志峰

(1.合肥工业大学，机械工业绿色设计与制造重点实验室，合肥，230009；2.合肥工业大学，合肥，230009)

0 序言

焊接在各个行业广泛应用，我国焊接行业每年金属消耗量达到420 万吨[1].钨极氩弧焊(gas tungsten arc welding,GTAW)因其生产的焊缝质量高，是目前制造业中广泛使用的金属连接技术之一[2-4].焊接过程所产生的烟尘、废气等环境负荷会对环境和人体造成一定的危害[5-7].焊接烟尘粒径非常小(<0.1 μm)且成份复杂[8-10]，包含元素多达20 种以上[11]；焊接废气包括CO2，NOx，SO2和O3等[12].这些物质都易通过呼吸进入身体对人造成健康危害[13]，严重可致癌[14].因此，有必要进一步采集焊接过程中所产生的环境负荷数据、分析焊接环境负荷特性，减小焊接过程对环境、从业人员的危害.

目前，由于焊接环境负荷的易扩散性导致难以采集或采集数据不精确，无法完全采用实测手段，需要进一步建立相关模型来表征焊接环境的产生量[15].Ioffe 等人[16]建立了焊接过程中烟尘产生的物理模型，揭示了熔滴从球状模式向喷雾模式转变时烟气生成率降低的现象.Dennis 等人[17]建立了适用于弧焊和喷焊过渡模式GMAW 烟尘排放模型，预测的烟尘形成率和测量的烟尘形成率之间存在一定程度的关系.Deam 等人[18]建立GMAW 的烟气形成半经验模型，模型表明雾滴尺寸和送丝速度可以控制细烟的形成速率.卜智翔等人[19]结合“质量—弹簧”理论，建立基于熔滴过渡模型的GMAW 焊接发尘率预测模型，预测其熔滴中的Fe 和Mn 元素蒸发率.Vimal 等人[20]以建立了焊条电弧焊焊接工艺BP 神经网络预测模型，对熔渣、飞溅、功耗、烟气生成率和颗粒形成这五个指标进行预测.这些模型有效阐述了相关因素与烟气形成速率之间的关系，但是均不能直接反应相关负荷的产生量.

针对GTAW 在密闭环境下所产生的NOx，O3，PM2.5，PM10等物质浓度，文中根据收集、获取的环境负荷排放数据建立其焊接环境负荷排放模型，分析基于关键工艺参数的排放特性，以帮助减小焊接对环境、从业人员的危害，也为焊接工艺环保标准体系进一步充实完善提供数据支撑.

1 试验方法

焊接工艺为GTAW，工艺设备为SZ-GCS04 多功能精密铝焊机，电源为单相220V-50Hz；电流范围为80～200 A；保护气体为Ar；使用ER4043 型铝焊丝对厚度为5 mm 的基材6061 铝板进行焊接，其化学成分如表1 所示.试验在密闭焊接环境(0.12 m3)下进行焊接.焊接环境负荷排放采集系统由焊接工作台、检测仪器以及软件工具组成，如图1所示.利用各传感器(采集频率：每秒1 次)来接收焊接过程中的初始数据，实现数据采集和分析.为保证数据质量，试验在密闭手套箱内进行，母材放置于传动装置上，焊枪固定于空间桁架装置，从而实现自动焊接.

表1 6061 铝合金化学成分(质量分数，%)Table 1 Chemical composition of aluminum alloy

图1 焊接环境负荷排放采集系统Fig.1 Welding environment load discharge acquisition system

2 试验设计

2.1 正交试验分析

试验所考虑的因素众多，包括焊接电流、喷嘴高度、保护气流速、焊接速度、焊接时间等.正交试验法是有效降低试验次数的一种设计方法[21].根据GTAW 工艺特点，选择喷嘴高度、焊接电流、焊接时间、保护气流速、坡口类型和焊接速度为试验因素，各因素均设3 个水平，各水平均有代表性，覆盖大部分实际焊接参数调节范围.按照L27(37)型设计27 组试验，如表2 所示.其试验结果如表3 所示，并对结果进行方差分析，确定关键焊接排放影响因素.

表2 正交试验因素及水平Table 2 Orthogonal factor test and level

表3 正交试验结果Table 3 Orthogonal test results

为了保证试验结果的准确性，同参数下试验重复3～5次，若前3 次测量结果误差超过20%，则需要加测2次，以多次试验结果的平均值为表征数据.

2.2 方差分析

计算各因素的偏差平方和、误差平方和、误差自由度等计算量，最后计算出F值，进行显著性检验.

其过程可表示为

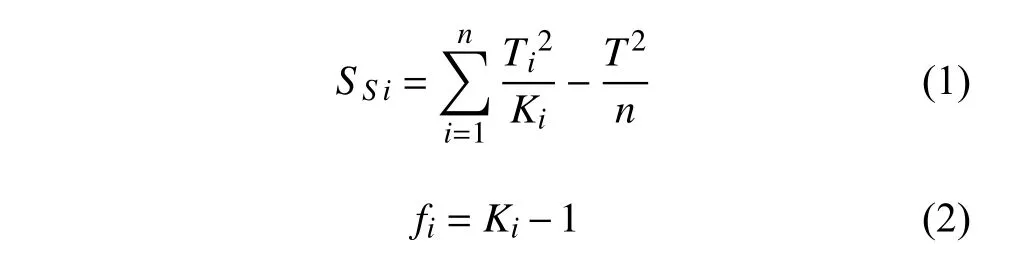
式中：SSi是各因素的偏差平方和，Ti是各因素同水平数据总和,Ki是各因素水平重复数，T是数据总和,n是数据总个数，fi是各因素的自由度.

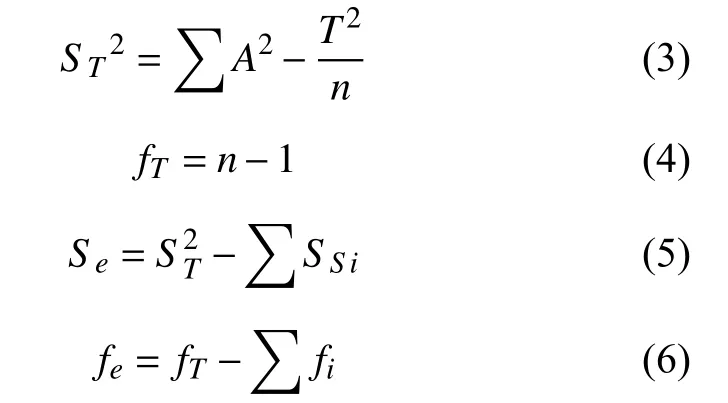
式中：ST2是所有因素的偏差平方和，A2是各试验的指标值，fT是所有因素的总自由度，Se是误差平方和，fe是误差自由度.

式中：MSi是各因素平均偏差平方，MSe是误差的偏差平方，Fi为检验统计量，F0.1(2,14)为临界标准值.

F值越大，表明影响程度越大，仅对各排放指标具有显著影响因素进行统计，即F值大于2.73.根据表4 和表5 可知，对NOx排放影响的显著因素依次为焊接电流、喷嘴高度、焊接时间；对O3排放影响的显著因素依次为喷嘴高度、焊接电流、焊接时间.对PM2.5与PM10排放影响的显著因素依次为焊接电流、喷嘴高度、焊接时间.综合试验结果，确定对焊接排放影响最为显著的因素为焊接电流、喷嘴高度、焊接时间.

表4 NOx 和O3 方差分析结果Table 4 Variance analysis of NOx and O3 results

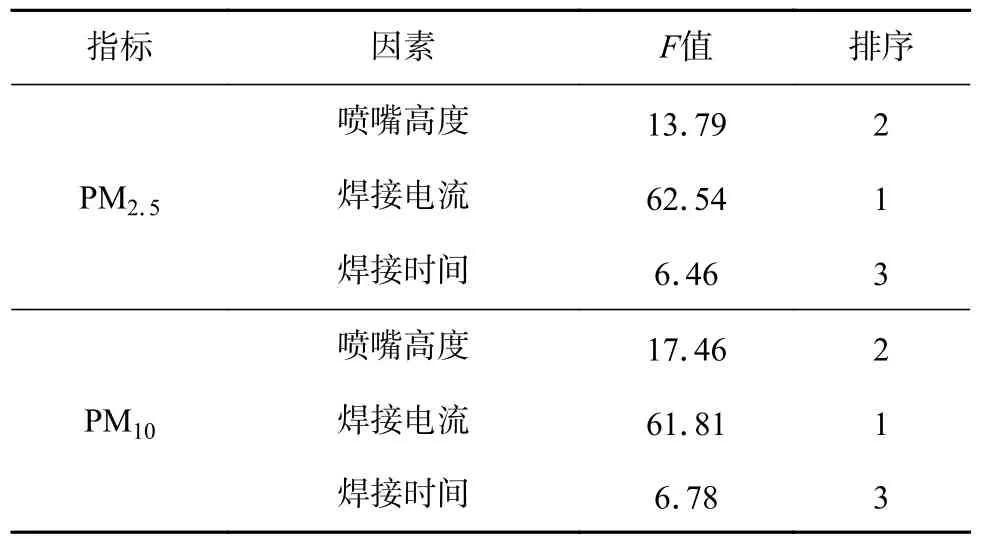
表5 PM2.5 和PM10 方差分析结果Table 5 Variance analysis of PM2.5 and PM10 results

3 预测模型建立

在数据分析领域，神经网络有着极为广泛的应用，尤其是在非线性数据预测建模方面[22].焊接环境负荷的产生受众多工艺参数影响，导致其产生量往往无明显规律.BP 神经网络、RBF 神经网络等方法在焊接力学性能[23]、焊缝形态预测方面[24]已取得较突出的应用效果.例如，朱师琦[25]以焊接电流、电压、速度以及保护气流速为输入，建立基于BP 神经网络建立GMAW 发尘率预测模型，对焊接发尘量进行预测且整体误差低于10%.文中综合考虑焊接烟尘和废气，采用RBF-BP 组合神经网络来搭建GTAW 焊接环境负荷数据排放预测模型.

以焊接电流，喷嘴高度，焊接时间这3 个关键工艺参数作为输入量，以NOx，O3，PM2.5，PM10浓度作为输出量，获取162 条样本数据，基于RBFBP 复合神经网络，构建GTAW 焊接环境负荷排放预测模型.

3.1 样本数据处理

随机划分样本数据的75%作为训练集，25%作为测试集.由于输入输出层各参数的量纲不同，数值上差距较大，为避免数值计算时出现大数淹没小数的现象，在模型训练前将各参数进行归一化处理.

式中：xmax为样本数据的最大值，xmin为样本数据的最小值.

3.2 建立RBF-BP 组合神经网络模型

将RBF 神经网络与BP 神经网络进行组合构建组合神经网络模型，其中RBF 神经网络的输出层作为BP 神经网络的输入层，以多层BP 神经网络作为连接层，同时以RBF 神经网络的输出层为组合神经网络模型的输出层，如图2 所示.

图2 RBF-BP 组合神经网络模型Fig.2 RBF-BP combined neural network model

BP 神经网络与RBF 神经网络的算法如下，对于BP 神经网络部分假设模型中的第j个神经元，有n个输入参数，分别用x1，x2，xn表示，各输入值对应的权值分别为w1，w2，wn，则从输入层到下一层神经元的输入值为z可由式(13)得出：

式中：zk为第k个神经元的输入值(1≤k≤J)，wi1为输入层到隐含层的神经元连接权重，b1为计算过程中的偏置，σ1为隐含层神经元的激活函数，aj为隐含层第k的神经元的输出.

由隐藏层到输出层的的计算过程为

式中：wi2为隐含层到输出层的神经元连接权重，σ2隐含层到输出层的的激活函数，b2为计算过程中的偏置，y为神经网络输出层的输出值.

RBF 神经网络的隐含层采用的是径向基激活函数,高斯径向基函数的表达为：

式中：其中ci为核函数的中心，xp为输入值，σ为函数的宽度参数，||xp−ci||表示为空间任意一点到高斯核函数中心的欧氏距离.

将选定的高斯径向基函数带入的计算过程即

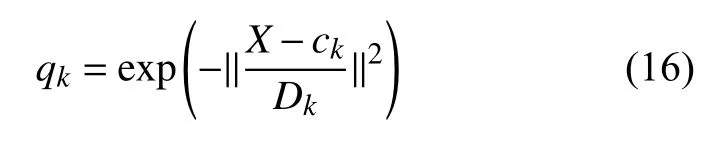
式中：qk为第k个神经元的函数输出值，X为输入参数的向量表达，ck为隐含层第k个神经元对应的中心向量，Dk为隐含层第k个神经元的宽度向量.

隐含层到输出层采用的是线性输出函数，其输出过程表达式为

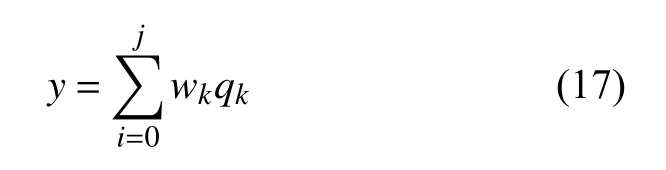
式中：j为隐含层神经元的总数，wk为隐含层到输出层的神经元连接权重，y为该神经网络的输出结果.

将RBF 神经网络与BP 神经网络进行组合构建组合神经网络模型，其计算过程为

输入层到RBF 隐藏层

RBF 隐藏层到连接层

连接层到BP 隐藏层

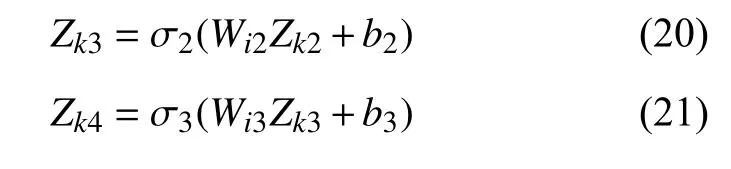
BP 隐藏层到输出层

式中：Wi1为隐藏层到连接层的权重系数的矩阵表达，Wi2，Wi3为连接层到BP 隐藏层的权重系数的矩阵表达，Wi4为BP 隐藏层到输出层的权重系数的矩阵表达.σ1σ2σ3为相应的激活函数.Zk1为RBF 隐藏层输出结果的矩阵表达，Zk2为连接层输出结果的矩阵表达，Zk3，Zk4为BP 隐藏层输出结果的矩阵表达，y为最终的输出结果.

组合模型有4 层隐藏层.第一层为RBF 神经网络隐含层，神经元为30个，以高斯径向基函数作为激活函数；第二层为连接层，用于连接两类神经网络、第三、四层为BP 神经网络层隐含层，神经元分别为45 个、30 个；激活函数分别sigmoid 函数、rule函数；且第四层Dropout 设置为0.1.以MSE 作为损失函数，采用Adam 优化算法，随机权重初始值，偏置初始值随机生成.

3.3 模型验证与比较

选取15 组未在训练集和测试集中出现过的特征参数进行试验，与神经网络的环境负荷排放产生量预测结果对比.并与相应的BP 神经网络与RBF 神经网络预测模型进行对比分析，遵循最小误差原则，调试出各个模型的最优参数，结果如图3，图4 所示.

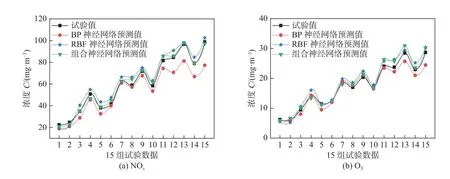
图3 三种神经网络与真实值对比情况(气体)Fig.3 Comparison between the three neural networks and the real value(gas).(a) NOx;(b) O3

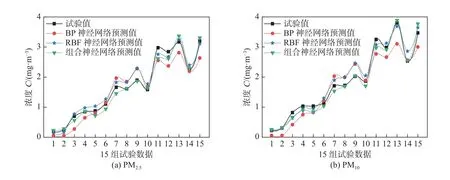
图4 三种神经网络与真实值对比情况(颗粒物)Fig.4 Comparison between the three neural networks and the real value(PM).(a) PM2.5;(b) PM10

BP 神经网络模型预测结果平均误差为17.09%(如表6 所示)，气体的产生量预测结果误差要低于颗粒物.且颗粒物产生量预测结果中出现较大的波动，预测误差最小值与最大值之间波动很大，会出现个别数据点的预测值远远偏离真实值的情况，该模型稳定性较差.RBF 神经网络模型预测结果平均误差为10.02%，气体的产生量预测结果误差要低于颗粒物.虽然颗粒物产生量预测结果仍有一定的波动，但是预测效果要好于BP 神经网络模型，尤其是在颗粒物的预测性能上有着较大提升.相比BP 神经网络模型，RBF 神经网络模型更能接近真实数值.RBF-BP 组合神经网络模型预测结果平均误差为6.63%，气体的产生量预测结果误差要低于颗粒物.相较于其他2 种模型，RBF-BP 组合神经网络模型预测结果与实际值拟合程度高，且稳定性更好.

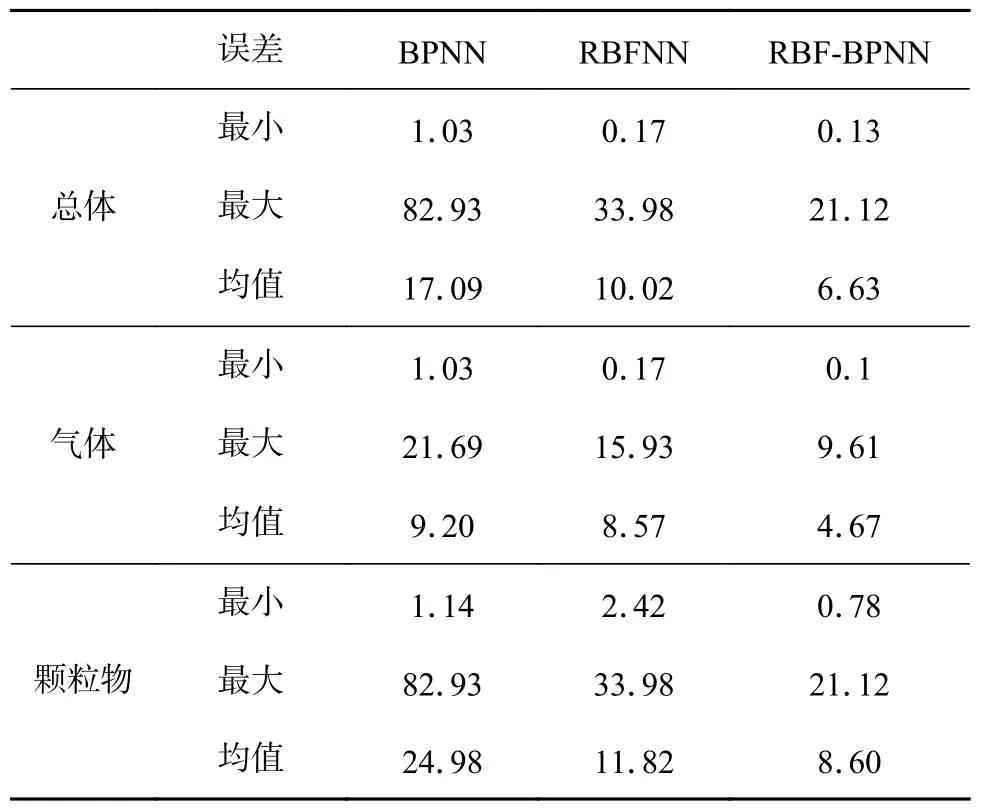
表6 三种神经网络误差对比(%)Table 6 Error comparison of three kinds of neural networks

从表7 可以看出，RBF-BP 组合神经网络模型的MSE 值(0.00203) 最小且R2值(0.83091)最大，对样本数据的拟合效果最好.而RBF 神经网络模型在2 个指标上的表现仅次于RBF-BP 组合神经网络模型，也符合试验结果.

表7 各模型性能评价指标Table 7 Performance evaluation indexes of each model

其次，通过神经网络模型也说明焊接参数与焊接排放之间具有可预测性，通过对焊接关键参数与排放结果之间的关联分析，发现焊接电流、喷嘴高度、焊接时间与焊接环境负荷排放呈正相关趋势，从而可为合理制定焊接工艺提供技术参考.

图5、图6、图7 分别为焊接时间、焊接电流、喷嘴高度对各环境负荷排放的影响规律.3 个焊接参数均对焊接过程中各环境负荷排放有显著影响.由图5 可知，随着时间的增加，NOx、O3、PM2.5与PM10产生量相应增大；由图6 可知，随着电流的增大，NOx、O3、PM2.5与PM10产生量也会增大，但颗粒物的产生量具有一定的波动性；由图7可知，随着喷嘴高度的增大，NOx、O3、PM2.5与PM10产生量相应增大.

图5 焊接时间对排放的影响Fig.5 Effect of welding time on emissions.(a) NOx;(b) O3;(c) PM2.5;(d) PM10

图6 焊接电流对排放的影响Fig.6 Effect of welding current on emission.(a) NOx;(b) O3;(c) PM2.5;(d) PM10

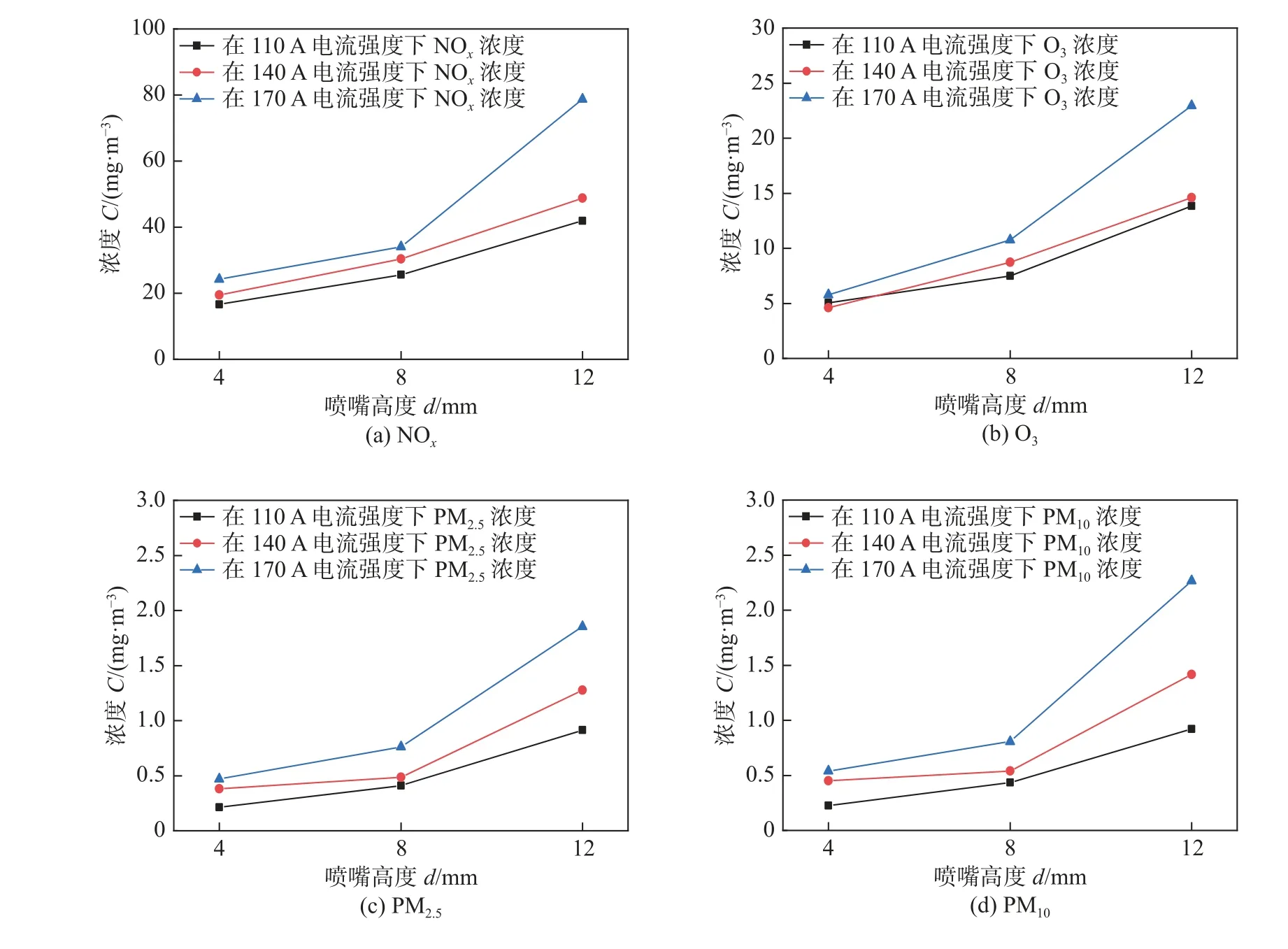
图7 喷嘴高度对排放的影响Fig.7 Effect of nozzle height on emissions.(a) NOx;(b) O3;(c) PM2.5;(d) PM10

4 结论

(1) RBF-BP 组合神经网络分析表明对焊接环境负荷的产生量预测平均误差6.63%.其中，气体预测结果平均误差为4.67%，颗粒物预测结果平均误差为8.60%.采用组合模型预测GTAW 的焊接环境负荷排放数据，可为减少焊接工艺环境负荷排放量提供指导.

(2) 对所建立的BP 神经网络模型、RBF 神经网络模型、RBF-BP 复合神经网络模型进行性能对比分析.RBF-BPNN 具有最小的MSE(0.002 03)、和最大的R2(0.830 91)，理论上该模型的性能最好，与试验结果相符合.

(3) 焊接排放最为显著的影响因素为焊接电流、喷嘴高度、焊接时间且与焊接环境负荷排放是呈正相关趋势；而焊接速度、保护气体流速、坡口类型这3 个因素对焊接环境负荷排放的影响不显著.