X70 管线钢在役焊接损伤演化模型与数值模拟

谷世伟，徐良，杨海锋，张洪杰，韩涛

(1.哈焊国创(青岛)焊接工程创新中心有限公司，青岛，266111；2.中国石油大学(华东)材料科学与工程学院，青岛，266580)

0 序言

老化和腐蚀问题影响着长输管线的安全运行，在役焊接修复技术可以在保证管道不停输的情况下对其进行修复，是一种安全、高效、环保的管道修复技术[1-3].

然而，烧穿是在役焊接面临的主要问题，在过去三十多年中，国内外学者针对烧穿问题进行了许多研究，美国BWI 研究所对烧穿预测进行了相关研究，并提出了内壁温度982℃为烧穿的临界温度[4].Cisilino 等人[5]从壁厚的角度研究烧穿问题，并指出壁厚6.4 mm 为烧穿的临界壁厚.Boring 等人[6]提出径向变形量0.38 mm 为临界变形量.郭广飞[7]从剩余强度的角度预测烧穿，并研究了温度、压力、壁厚和管径等因素对剩余强度的影响规律.Wu 等人[8]对剩余强度法进行了优化，并建立了热输入与积分温度下限的线性表达式.Majnoun 等人[9]通过引入“剩余厚度”这一临界参数，建立了一种新的热力学判据预测烧穿.目前，国内外学者对在役焊接烧穿预测的研究仅仅考虑烧穿瞬间各项指标，而不能有效地基于理论将烧穿量化，缺乏对烧穿过程演化的分析.

连续介质损伤力学的发展为研究在役焊接烧穿过程提供了新思路.Lemaitre[10]基于连续损伤力学建立了损伤与累计塑性应变的线性表达式，用于预测金属的韧性开裂.Oyane[11]考虑了静水应力对韧性断裂的影响，并建立了相关断裂准则.Bonora等人[12-13]在Lemaitre 准则的基础上，考虑了初始损伤阈值应变、临界损伤断裂应变、临界损伤值对金属形变过程中损伤演化的影响.杨超众[14]基于Bonaro 模型，建立了316LN 钢的高温损伤演化方程，并通过试验验证了该方程能够较好地预测该材料的热成形开裂问题.

试验采用数学建模、有限元模拟和试验相结合的方式，构建在役焊接过程中的高温损伤演化方程，研究在役焊接过程中的损伤演化规律，分析不同因素对损伤演化的影响规律.

1 试验方法

1.1 高温拉伸试验

在役焊接过程中，熔池下方金属的形变行为与其高温性能参数密切相关，因此研究在役焊接过程中的失效行为，有必要通过高温拉伸试验获得X70 管线钢母材高温性能参数.试验中设定温度分别为1 000，1 100，1 200，1 300 ℃.根据前期在役焊接数值模拟结果，设定试样拉伸变形的应变速率为0.1/s 和1.0/s.

试样在拉伸之前，需以10 ℃/s 的速度加热到1 350 ℃，并在此温度下保温5 min，然后以相同的速度冷却到设定温度进行拉伸试验，获得的应力应变曲线如图1 所示.

图1 真应力-真应变曲线Fig.1 Ture stress vs.true strain curve.(a) 0.1/s; (b) 1.0/s

1.2 在役焊接试验

在役焊接所采用的试验装置如图2 所示，为模拟实际在役焊接过程中管道的带压焊接，采用水泵和节流阀实现焊接工件夹具两端进水口和出水口介质流速的差异，从而实现焊接工件内部的带压，通过调节节流阀改变出水口的介质流量从而实现为焊接工件内部压力的不同.

图2 在役焊接试验装置Fig.2 Test device of in-service welding

焊接方式采用不填丝TIG焊，X70 试管管径为114 mm，壁厚为4 mm，试验参数及烧穿情况如表1 所示.

表1 在役焊接试验相关工艺参数Table 1 Welding parameters of in-service welding

可以发现前5 组试验均未发生烧穿，当热输入增大到980 J/mm时，发生烧穿失效.

2 BONARO 模型数学建模

2.1 BONARO 数学模型

在多轴加载中，Bonaro 准则为

式中：D表示材料累计损伤值；D0表示初始损伤值；Dcr表示临界损伤值；P表示累计等效塑性应变；Pcr表示多轴应力状态下的临界损伤断裂应变；Pth表示多轴应力状态下初始损伤断裂应变；εth表示单轴应力状态下的初始损伤阈值应变；εcr表示单轴应力状态下的临界损伤断裂应变；ν表示泊松比；表示应力三轴度；α表示损伤因子；σm表示等效应力；表示静水应力.

2.2 损伤模型参数的确定

使用Bonaro 模型描述材料的高温失效行为需要5 个材料参数：εth，εcr，Dcr，D0，α.一般认为初始材料内部不存在损伤，即D0=0，对于钢类材料 α=0.45～0.6，文中取α=0.5[15]，因此需要确定的材料参数仅剩 εth，εcr，Dcr.

根据文献[16] 所提方法，初始损伤阈值应变εth可用载荷行程曲线最高点对应应变代替，临界损伤值可由如下公式计算

式中：σR表示断裂应力；σu表示峰值应力.

临界损伤断裂应变 εcr采用文献[14]所提方法进行确定，结果如表2 所示.

表2 损伤模型参数结果Table 2 Damage model parameter results

流变应力与温度和应变率的关系可以用Z 参数表示为[17]

式中：Z表示温度补偿速率因子；R表示气体常数；Q表示变形激活能.

试验主要通过Z参数建立 εth、εcr、Dcr与温度和应变率之间的关系式，材料高温形变过程中，可用Arrhenius 方程的幂函数形式来描述流变应力与温度和应变率的关系为[18]

式中：A1表示材料常数；n1表示加工硬化指数.

对材料参数进行数学建模前需确定X70 管线钢的变形激活能Q，由公式(6)可以推导出变形激活能Q的表达式为

根据表2，对不同温度、不同应变率下的峰值应力进行最小二乘法拟合，可以求得Q=408.77 kJ/mol.

根据表2 中的数据对 εth，εcr，Dcr进行数学建模，参照参数Z的表达式形式，分别采取应变速率的指数形式和温度倒数的指数形式作为自变量进行拟合，得到 εth，εcr，Dcr与温度和应变速率的表达式，误差分别为1.62%、1.23%和0.5%.结合Bonaro 损伤模型，得到X70 管线钢高温损伤演化方程.

3 在役焊接数值模拟

为了分析在役焊接过程中的损伤演化规律，在试验结束后，对在役焊接温度场和应力应变场进行数值模拟并耦合X70 管线钢高温损伤演化方程.

基于试验管道的几何形状，建立三维有限元模型，为节约计算时间，焊接接头区域采用密集网格，而其他区域采用稀疏网格，通过前期网格敏感性计算，建立如图3 所示半管模型，最大网格尺寸为2 mm × 5 mm × 6 mm，最小网格尺寸为0.25 mm ×0.5 mm × 0.35 mm.

图3 管道模型Fig.3 Model of the pipeline.(a)3D model of half pipeline; (b) 2D model of welded joint

采用Goldak 等人[19]提出的双椭球热源进行数值模拟，该热源模型充分考虑了电弧能量非对称分布的特点，广泛应用于电弧焊的数值模拟中；依据试验管道内压情况和装卡情况，对管道模型内壁施加垂直于模型内表面指向外的均匀压力，对管道模型两端施加刚性约束.

在役焊接过程管道外表面与空气的换热方式主要有自然对流和辐射；对于工件内表面，则必须考虑内壁与介质的强制对流，在试验中，外壁换热系数取29 W/(m2·℃)，内壁换热系数取1 800 W/(m2·℃)[20].

4 结果和分析

4.1 损伤演化过程分析

根据试验结果分析可知，当热输入由955 J/mm增达到980 J/mm时，发生烧穿失效，因此选取这2 组试验参数进行分析.为方便对在役焊接过程中熔池下方区域损伤值进行分析，规定热源正下方-熔深最大处-熔池末端的取点路径，如图4 所示.

图4 取点路径Fig.4 Point path

首先对热输入为955 J/mm 时的损伤请况进行分析，图5a 和图5b 分别为5.75 s 时路径B1 至X8 内壁点和路径X4 上熔合线至内壁的损伤值的分布图，可以看出损伤在热源正下方靠后的位置才开始积累，最大损伤值出现在熔深最大处后方的位置，且壁厚方向上，损伤值由熔合线向内壁逐渐减小.

图5 不同路径损伤分布Fig.5 Distribution of damage values in differnet paths.(a) Path from B1 to X8; (b) Path X4 from weld line to the inner wall

图6 展示了路径X4 由熔合线至内壁方向上各节点的损伤值随时间的变化请况，可以看出，4.75 s时，各节点损伤值均为0，5 s时，熔合线附近节点出现损伤，并随时间逐渐增大，且在任意时刻下，熔合线处损伤值均大于内壁处，这说明在役焊接过程中，熔合线位置更容易萌生损伤.

图6 路径X4 不同时刻损伤值Fig.6 Damage values at different time at path X4

接下来对热输入980 J/mm 的损伤分布请况进行分析，图7 展示了路径X1 至X5 方向上内壁节点在5～6 s 时间段内的损伤演变请况，可以看出内壁上最大损伤值出现在熔深最大处后方1.4～1.8 mm区域内，路径X2 至X5 内壁节点损伤值在5.75 s和6 s 时相同，这说明损伤值并不会无限增大，且从时间角度来看，最大熔深处后方1.4 mm 位置的损伤值最先达到最大值.图8a 和图8b 分别为5.5 s和5.75 s 路径X1 至X5 内壁节点损伤值与临界损伤值的对比图，可以看出，5.5 s 时内壁节点损伤值均小于其对应的临界损伤值，即未发生烧穿失效；而5.75 s 时X2，X3，X4 内壁节点的损伤值达到其对应的临界损伤值，即这些位置发生失效，这与试验过程中第6 组发生烧穿的情况相吻合，同时，发生失效的节点位于最大熔深处后方1～2 mm 区域内，这与文献[21] 中结论相符，这说明所建立的X70 高温损伤演化方程能够较好地预测在役焊接过程中的损伤演化情况.

图7 不同时刻损伤值分布Fig.7 Distribution of damage values at different time

图8 损伤值与临界损伤值的对比Fig.8 Comparison of damage and critical value.(a) 5.5 s;(b) 5.75 s

4.2 管道内压对在役焊接损伤演化的影响

在保证在役焊接热输入980 J/mm、管道壁厚4 mm 的情况下，进行不同管道内压(1.5，2.5，3.5，4.5，5.5，6.5 MPa)下的在役焊接数值模拟，并耦合所建立的损伤演化方程.

图9 展示了不同内压下5.75 s 时路径B1 至X8 内壁节点的损伤值分布情况，可以看出，内壁损伤值随内压的增大而增加；图10 展示了5.75 s 路径X4 上节点损伤值分布情况，可以看出，不同内压下，由熔合线至内壁的损伤分布趋势基本一致，均由熔合线至内壁递减，当管道内压为1.5 MPa时，路径节点损伤值均为0，这说明损伤萌生存在临界内压.

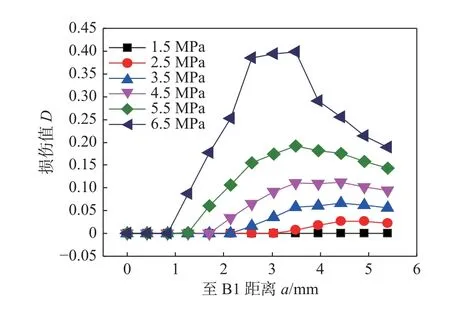
图9 不同压力下的损伤分布(B1-X8)Fig.9 Distribution of damage values at different pressure(B1-X8)

图10 路径X4 损伤分布Fig.10 Distribution of damage at path X4

从累计塑性应变P和临界损伤断裂应变Pcr的角度解释压力对在役焊接损伤失效的影响，图11展示了路径X4 上内壁节点的累计塑性应变和临界损伤断裂应变随内压的变化请况，通过分析可知，随着管道内压的增大，内壁累计塑性应变逐渐增大，临界损伤断裂应变则逐渐减小，且管道内压的变化对累计塑性应变的影响幅度更大，当内压达到6.5 MPa时，累计塑性应变等于临界损伤断裂应变，内壁发生损伤失效，这说明在役焊接过程中，管道内压越大，烧穿失效的风险更高.

图11 路径X4 损伤值与临界损伤值对比Fig.11 Comparison of damage and critical value at path X4

4.3 壁厚对在役焊接损伤演化的影响

在保证焊接热输入980 J/mm、管内介质压力6.5 MPa 的情况下，采用不同壁厚(4.0 mm、4.2 mm、4.4 mm、4.6 mm)的管道模型进行在役焊接数值模拟，并耦合缩得到的损伤演化方程.

图12 为不同管道壁厚下路径B1 至路径X8 内壁节点的损伤分布图，可以看出，随着管道壁厚的增加，内壁内壁损伤值明显减小，且损伤萌生位置越靠后，当管道壁厚为4.6 mm时，熔池下方内壁位置不会萌生损伤.

图12 不同壁厚下的损伤分布Fig.12 Distribution of damage at different wall thickness

图13 为不同管道壁厚下路径X4 熔合线至内壁方向上各节点的损伤分布图，可以看出，壁厚方向上的损伤值随管道壁厚的增加而减小，且壁厚的增加有利于缩小熔合线附近损伤萌生区域.这说明在役焊接管道壁厚越大，损伤萌生和烧穿失效的风险越小.

图13 路径X4 损伤分布Fig.13 Distribution of damage at path X4

从温度T、累计塑性应变P和临界损伤断裂应变Pcr的角度解释压力对在役焊接损伤失效的影响，图14 展示了路径X4 内壁节点温度、累计塑性应变和临界损伤断裂应变随管道壁厚的变化请况，可以看出，随着管道壁厚的增加，内壁节点的临界损伤断裂应变增大，而累计塑性应变减小，通过分析这种变化趋势可知管道壁厚越大，发生烧穿失效的风险越低；同时，内壁温度随管道壁厚的增大而逐渐降低，内壁温度是导致在役焊接烧穿失效的重要因素之一[7]，内壁温度的降低同样有利于降低烧穿失效的风险.

图14 路径X4 温度、损伤值与临界损伤值对比Fig.14 Comparison of temperature，damage and critical value at path X4

5 结论

(1) 基于Bonaro 准则建立了X70 管线钢高温损伤演化方程，通过在役焊接试验验证了该方程在预测在役焊接烧穿失效行为的准确性.

(2) 在役焊接过程中，熔池下方熔深最大处后方1～2 mm 区域为失效高风险区，壁厚方向上，损伤值由熔合线向内壁逐渐减小，熔合线附近区域比内壁更容易萌生损伤，且该区域损伤值更大.

(3)临界损伤断裂应变随管道内压的增大而减小，随管道壁厚的增大而增加.

(4)降低管内介质压力、增大管道壁厚有利于降低在役焊接熔池下方萌生损伤甚至烧穿失效的风险.