结合专家信任的协同过滤推荐算法研究

刘国丽，徐洪楠，谭有倩

(1.河北工业大学人工智能与数据科学学院，天津 300401； 2.河北工业大学廊坊分校，河北 廊坊 065008)

0 引 言

互联网时代导致的信息过载现象，促使电子商务社区对推荐算法进行大量改进，以提供一种智能机制，从与用户相关的海量数据中过滤出可用的信息。协同过滤是推荐系统中应用最广泛的推荐技术之一[1]。传统的协同过滤算法主要是依靠邻居用户进行推荐，这样仅依赖邻居用户所得到的推荐结果往往不是很可靠。在现实生活的社交网络中，不仅有兴趣相似的邻居用户，还存在具有某些特定领域知识并且阅历广泛的社区专家[2]。在人们的日常生活中，人们倾向于咨询专家，听取专家意见。专家的建议更具有说服力，也会影响用户的感知[3]。因此，越来越多的学者将专家信任因素考虑到推荐系统中。

针对目前协同过滤推荐算法存在的邻居用户相似度、专家信任度计算不准确、冷启动等原因导致的推荐准确度低的问题，国内外学者进行了大量研究。李炎等人[4]从用户空间角度对相似度以及评分预测进行改进，在提高了算法准确率的同时也降低了算法的时间复杂度，但忽略了项目本身的冷门程度对相似度的影响。Hafed等人[5]引入项目场景相似度的概念，对相似度计算公式进行改进，提出了一种新的基于场景的协同过滤推荐算法，最终利用聚类矩阵和用户的评分矩阵生成推荐，有效地缓解了稀疏性问题，提高了推荐精度。Gou等人[6]将信任感知和领域专家推荐相结合，通过信任感知网络解决不能直接计算某些用户的信任值的问题，但在相似度计算上，忽略了用户的评分时间对相似度的影响。李普聪等人[7]借鉴社会心理学人际信任建立机制，将“用户-项目”单层网络扩展为“用户-用户-项目”双层网络，根据用户之间的信任确定资源分配，提高了推荐的准确度和多样性。Wu等人[8]认为进行预测时的关键问题是检测不可信用户提供的不可靠数据，从此角度，提出了一种新的可信性感知预测方法，采用两阶段K-means聚类来识别不可信用户，不仅提高了预测精度，而且提高了方法的鲁棒性。Ahlem等人[9]提出了一种基于信任的服务推荐机制，该机制分为2个阶段，第一阶段根据用户的社会概况以及某段时间内的互动来对用户进行信任检测；第二阶段将社会性和协作性结合起来，根据专业水平向用户推荐适当的服务，该机制有效地提高了推荐精度。Zheng等人[10]将专家信任考虑到推荐算法中，有效地缓解了数据稀疏性和冷启动问题，但是在计算专家信任时，只考虑到了用户的评分数量，忽略了专家自身的社会阅历的影响。

上述算法虽然在提高推荐精度方面有一定的效果，但仍存在需要改进的地方，这体现在如下4个方面：1)已有的协同过滤推荐算法在计算相似度时，忽略了2个用户对同一项目评分时间所蕴含的隐偏好,本文通过用户的评分时间以及项目的产生时间形成隐偏好因子对相似度进行改进；2)考虑到2个用户公共偏好项目的冷门程度对相似度的影响，设置项目冷门因子，冷门因子越大，则2个用户公共偏好项目的冷门程度越高，该项目在用户的兴趣权重分配值越大，对相似度计算影响越大；3)鉴于以往专家信任的计算未考虑到专家的阅历值对信任值的影响，通过设置时间跨度因子体现专家的阅历值，专家的阅历越丰富，专家的评分越可靠，对用户的评分预测更加准确；4)上述算法对冷启动问题考虑仍不够全面，当用户不存在评分时，无法找出其邻居用户，因此无法进行有效的推荐。本文通过用户自身所具有的属性，找出与待测用户属性相似的用户，并联合专家用户来缓解冷启动问题。

1 结合专家信任的协同过滤推荐

针对传统推荐算法所存在的问题，本文提出一种结合专家信任的协同过滤推荐算法CFRAET(Collaborative Filtering Recommendation Algorithm based on Expert Trust)。传统的推荐算法将所有的用户群都作为选择最邻居用户的参考群，随着用户群的增加，不仅会降低系统的性能，还会造成严重的数据稀疏问题[11]。因此，本文首先参考文献[12]，根据用户的相似度进行聚类，将兴趣点相同的用户分到同一个社区簇中。本文算法从相似度、专家信任度和缓解冷启动3个方面进行研究。

1.1 相似度计算方法

对于个性化推荐来说，最核心的部分是相似度的计算。在相似度计算方法中，Pearson相关系数[13]和Jaccard相似系数[14]是应用较为广泛的2种。Pearson相关系数是根据2个用户的共同评分项计算相似度，适用于评分数目较多的数据集，但是忽略了2个用户公共评分项目所占的比例问题；Jaccard相似系数仅关注用户是否对项目进行过评分，而不考虑用户对项目的评分值。因此Jaccard相似系数主要用于计算有限集合中样本之间的相似度，适用于稀疏度高的数据集。本文参考文献[15]中的方法，通过引入加权系数，将Pearson相关系数和Jaccard相似系数结合在一起，有效地利用2种方法的优点，使相似度计算更加准确，计算如公式(1)所示：

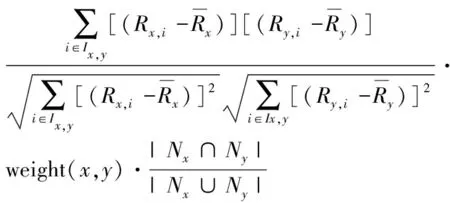
(1)

其中，Ix,y表示用户x、y的共同评分项集合，Rx,i、Ry,i分别表示用户x、y对项目i的评分，¯Rx表示用户x的平均评分，Nx、Ny分别表示用户x、y的评分项目集合，加权系数如公式(2)所示：

(2)

其中，Ix表示用户x已评分的项目集合，Iy表示用户y已评分的项目集合。

公式(1)虽将2种相似度计算方法的优点相结合，但是仅通过评分计算用户的相似度仍存在偏差。因此，本文将从公共评分项目蕴含的用户隐偏好及项目本身的冷门程度2个方面对相似度进行改进。

1.1.1 引入用户隐偏好

在现实生活中，当有新的项目产生时，人们会通过各种渠道提前了解到该项目的相关信息。以电影为例，当有新的电影即将上映时，电影所属的公司会对该电影进行宣传，用户可以通过各种渠道提前了解到电影的相关信息，如电影类型、演员阵容、电影内容等。用户会对该电影有一个定位，如果用户喜欢该电影，通常会尽早地观看其感兴趣的电影并对其评分；反之，如果用户不喜欢该电影，可能在电影上映很久以后才做出评分。电子产品中的手机也存在类似情况，每当有新型手机即将上市时，手机的厂家都会举办发布会，目的是让用户可以提前了解到手机的性能。若用户觉得该产品满足自己各方面的要求，用户就会在产品正式销售的第一时间去购买并评价该产品；反之，若该手机的某些指标没有满足用户的要求，该用户有可能会延迟购买的时间，或拒绝购买该产品。考虑到上述现象，可以认为用户对项目评分的时间与商品的产生时间在一定程度上反应用户对项目的偏好。因此，本文通过引入相对时间的概念来体现用户对项目的隐偏好。相对时间主要通过用户对项目的评分时刻与项目本身的产生时刻的差值来计算，相对时间值越大，表示用户对项目的隐偏好越小，反之，则越大。其计算如公式(3)所示：

pre(x,i)=URtime(x,i)-MRtime(i)

(3)

其中，URtime(x,i)表示用户x评价项目i的时刻，MRtime表示项目i的产生时刻。

考虑到2个用户对项目的隐偏好对相似度计算的影响，计算出2个用户的隐偏好差值，通过公式(4)对其进行规范化处理：

(4)

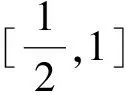
(5)

1.1.2 引入项目冷门因子

传统的结合专家信任的协同过滤推荐算法在计算相似度时，注重用户评分及用户自身属性带来的影响，但忽略了项目本身冷门程度对相似度的影响。通常情况下，若2个用户的共同偏好项越冷门，则该项目在相似度计算中权重也较大。因此，本文引入项目的冷门因子来对相似度进行改进。

对于每个项目，首先通过公式(6)计算出对该项目未评过分的用户数目，即项目的冷门度：

Unpopi=n-count(Rx,i>0)

(6)

其中，n表示用户的总个数，count(Rx,i>0)表示对项目i做出过评分的用户数量。

对用户公共评分项进行冷门因子的度量。2个用户的共同评分项集合Ix,y中会出现以下3种情况：

情况1 2个用户同时喜欢的项目集合。

情况2 2个用户同时不喜欢的项目集合。

情况3 一个用户喜欢而另一个用户不喜欢的项目集合。

对于情况1和情况2，2个用户对同一项目具有相同的偏好，此时，项目冷门因子对相似度的影响较大，采用公式(7)进行计算：

(7)

其中，Unpopmax表示项目的最大冷门度，其取值为Unpopi中的最大值，Unpopmin表示项目的最小冷门度，其取值为Unpopi中的最小值。

对于情况3，2个用户对同一项目的偏好不同，此时项目冷门因子对相似度的影响将会降低。本文采用2个用户的评分差值来降低冷门因子对相似度产生的影响，采用公式(8)进行计算：

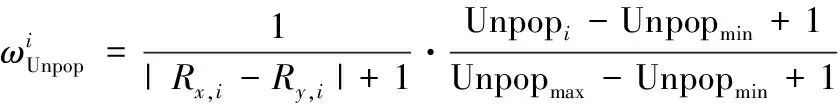
(8)

冷门因子介于0与1之间。通过公式(9)计算2个用户公共评分项集合的冷门因子的平均值：

(9)

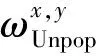
(10)

1.2 专家信任度计算方法

专家信任度表明用户向网络中的其他用户提供可靠信息的能力，该能力与用户储备的知识以及经验息息相关。景民昌等人[16]认为专家信任度与用户对项目的评分数量成正比，即用户的评分次数越多，则专家信任度值越高。专家信任度值计算方法如公式(11)所示：

(11)

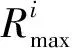
实际生活中，专家信任度不仅与评分数量有关，还与用户的阅历丰富程度有关[17]。本文从用户评分时间出发，考虑到不同阅历值对专家评分的影响，当用户阅历丰富时，用户会有更多的机会接触各式各样的项目，做出的评价就会更加可靠，专家信任度会更高。本文引入时间跨度因子反映专家的阅历丰富程度，计算方法如公式(12)所示：

(12)

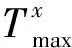
时间跨度因子φx不是一个固定的数值，会随着用户对项目评分的时间不同而发生变化。φx变化时，用户的专家信任度也会发生变化。本文专家信任度计算如公式(13)所示：

TStrust(x)=trust(x)·φx

(13)

专家信任度是选取专家的重要依据，但仅计算出专家信任度还不能完成目标用户的推荐，还应选出目标用户所在社区簇中的专家用户。通常有2种方法确定各社区簇中专家数目，第一种方法是固定专家的数目，即每个社区簇中专家的数目相同。由于每个社区簇中的用户数目是不确定的，如果固定专家的数目，可能出现整个社区簇中全是专家的极端情况。第二种方法是按照比例选取社区簇中专家的数目，该方法不仅会避免第一种方法中极端情况的产生，同时符合实际情况。因此，本文首先对社区簇内的每个用户按照专家信任度进行排序，然后按比例确定相应数目的用户作为该社区簇内的专家进行推荐。专家选取方法如公式(14)所示：

Expert(s)=Nums×γ

(14)

其中，Expert(s)表示第s个社区簇中的专家数量，Nums表示第s个社区簇中的全部用户数量，γ表示专家用户数所占该社区簇总人数的比例。

1.3 解决冷启动计算方法

用户冷启动问题，即用户不存在评分记录，用户不存在评分记录则无法找出其邻居用户进行推荐。针对用户冷启动问题，本文考虑到相同属性的用户具有相似的兴趣爱好，可以通过目标用户的自身属性寻找邻居用户。本文首先选出对待预测项目已评分的用户，其次对其中的专家用户采用专家信任度；对其中的普通用户，计算其与目标用户的属性相似度，最后通过属性相似用户与专家用户共同为冷启动用户产生推荐。

不同属性对用户兴趣的影响不同，其中，年龄和性别对兴趣的影响最大[18]。例如：对年龄而言，儿童倾向于观看卡通类影片，青少年倾向于动作类影片，中年人倾向于观看家庭伦理类影片，老年人则倾向于观看纪录片；对性别而言，男性倾向于观看断案推理类或者科幻动作类影片，女性倾向于看情感生活类或者喜剧类影片。因此，本文选取年龄和性别来计算用户之间的属性相似度。

1.3.1 用户属性预处理

为了方便属性相似度的计算，首先对数据集中的属性作数值化处理。对于性别，本文用“1”表示女性，“0”表示男性。对于年龄，由于在某一年龄段内用户兴趣爱好偏差不大，比如，13～17岁更倾向于看校园剧，因此，根据年龄分段如表1所示。将年龄分段之后，考虑到不同年龄段间的差异程度各不相同，比如，年龄段一与年龄段二的差异要远小于年龄段一与年龄段六的差异，因此本文通过顺序编码的方式将各个年龄段数值化，这样，在反应不同年龄段的差异的同时，也可降低因编码方式对相似度计算产生的影响。

表1 年龄数值化表

1.3.2 用户属性相似度

用户x与用户y的属性相似度计算如公式(15)所示：

其中，xage表示用户x的年龄，yage表示用户y的年龄，xsex表示用户x的性别，ysex表示用户y的性别，λ表示权衡因子，用来调节性别和年龄的比例。

1.4 评分预测计算方法

根据相似度将目标用户划分到相应的社区簇内，通过公式(10)计算出目标用户与所在社区簇中其他用户的相似度，并选出其邻居用户。通过公式(13)计算出用户的专家信任度，并按照一定比例选出专家用户。通过目标用户所在社区簇中的相似用户以及专家用户共同为该用户进行评分预测。改进后的评分预测如公式(16)所示：

(16)

其中，Px,i表示用户x对项目i的预测评分，TStrust(x1)表示第s个社区簇内的专家的信任值，x1表示社区簇内专家用户，Rx1,i表示专家的评分，x2表示社区簇内相似用户，K表示用户x的相似用户数量。α、β是平衡因子，用来调节专家用户与相似用户的比例。

通过公式(16)可以看出评分预测的前提是用户有过评分记录，通过评分记录可找出目标用户的相似用户，对于冷启动用户，公式(16)便不再适用。

在用户不存在评分记录或者评分记录极少，无法通过评分推断其兴趣爱好的情况下，可以通过专家用户为其推荐。专家用户评分客观，具有权威性，传统的协同过滤推荐算法使用专家用户为冷启动用户进行推荐，虽然可以有效地解决冷启动问题，但是在个性化推荐方面有所欠缺[19]。本文采用用户的自身属性来解决传统的推荐方法中个性化方面欠缺的问题。将属性相似用户与专家用户联合起来产生推荐，能有效地弥补传统算法中的不足。

冷启动用户的评分预测方法如公式(17)所示：

px,i=

(17)

其中，k表示社区簇个数，集合U为对项目i评过分的用户集合。

1.5 CFRAET算法流程

基于以上对算法的改进，本文提出的CFRAET算法流程如下：

Step1根据2个用户的评分时间以及项目的产生时间生成用户隐偏好因子。

Step2根据用户的评分矩阵计算出项目的冷门因子。

Step3根据用户参与评分项目的时间，计算每个用户的时间跨度因子，将时间跨度因子加入专家信任度的计算公式中，计算出每个用户的专家信任度。

Step4将用户隐偏好因子及项目冷门因子加入到相似度计算公式中，计算出用户间的相似度。

Step5将目标用户依据相似度划分到相应的社区簇中。

Step6判断用户的评分数量是否为冷启动用户，即用户对项目的评分数目是否为0。若为冷启动用户，此时跳转到Step8进行推荐，否则采用Step7进行推荐。

Step7在目标用户所在社区簇中确定其邻居用户和专家用户，通过二者共同为目标用户产生推荐。

Step8通过专家用户与目标用户的属性相似用户进行推荐。

CFRAET算法流程图如图1所示。

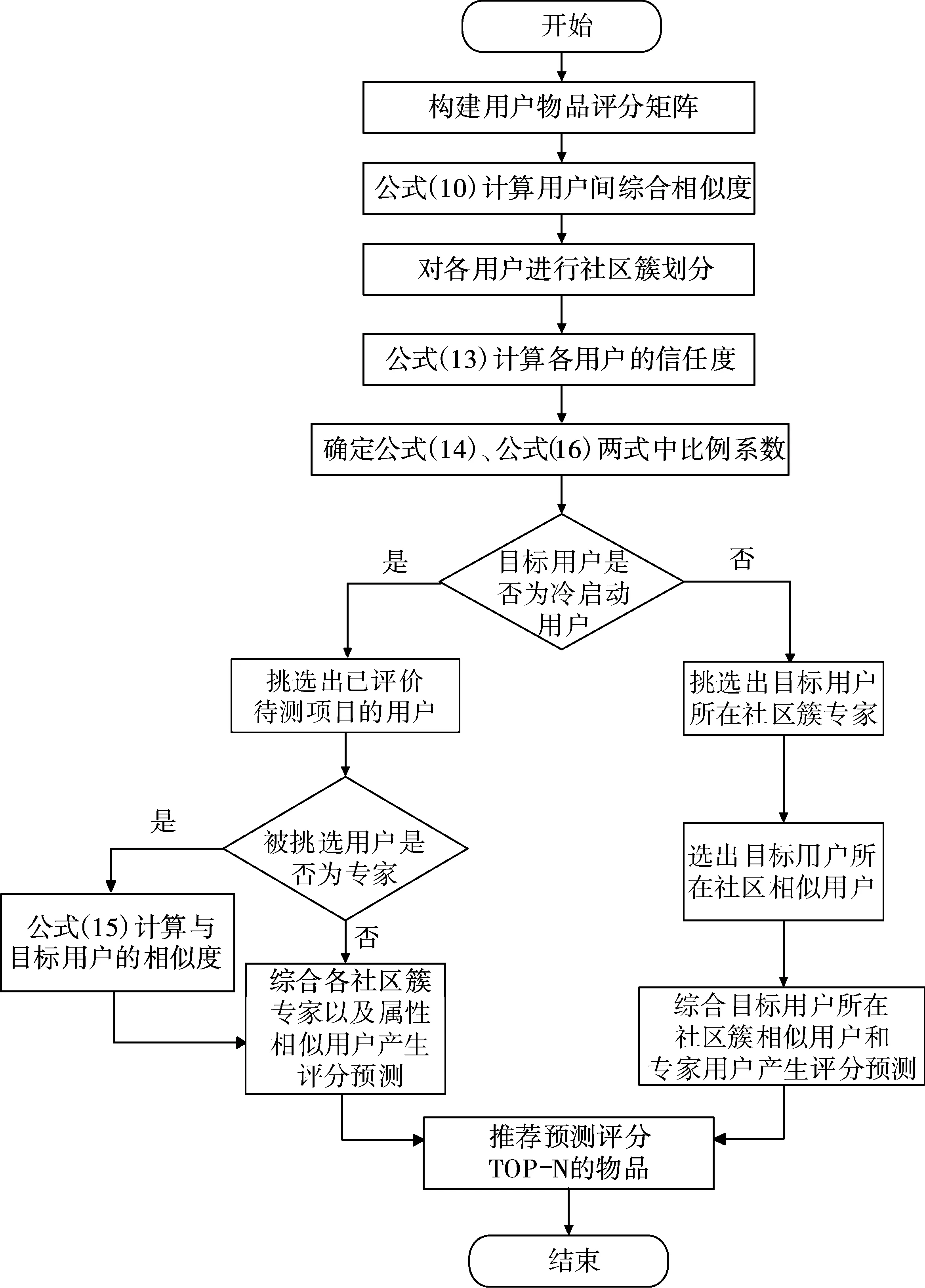
图1 CFRAET算法流程图

2 实验与分析

2.1 数据集及环境

本文采用Grouplens工作组提供的MovieLens-100k公开数据集来验证本文提出的算法CFRAET的有效性，该数据集包括943个用户、1682部电影以及每位用户对电影的评分数据，评分数据采用五分制进行评分，共计10万条[20]。在进行实验之前，将实验数据集划分为训练集和测试集2个部分，其中80%数据作为训练数据集，另外20%数据作为测试数据集。

实验所用环境为Windows10-64位操作系统，16 GB内存。算法由Python语言实现，IDE为Pycharm。

2.2 评价标准

2.2.1 基于预测的评分值进行评估

基于模型预测值的评价是指通过比较模型预测值与实际评分值，以模型的准确性为基础的评价方法。本文采用平均绝对误差MAE(Mean Absolute Error)测量预测评分与用户的真实评分之间的平均绝对偏差。MAE值越小，推荐精度越高[21]。MAE计算方法如公式(18)所示：

(18)

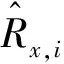
2.2.2 根据推荐结果进行评估

基于模型推荐结果的评估是一种通过将模型的推荐结果与用户的实际选择进行比较来衡量模型有效性的方法。本文采用了准确率Precision来衡量，Precision值越高，该模型推荐效果越好[22]。准确率计算方法如公式(19)所示：

(19)

其中，R(x)表示对用户x推荐的项目个数，T(x)表示测试集合中用户x的结果集合。R(x)∩T(x)表示正确推荐给用户u的项目个数。

2.3 实验参数设定

2.3.1 确定社区簇数目

MovieLen数据集中所包含的电影类型如表2所示，共19种。从表2可以看出，有些电影类型是相似的，比如儿童类和卡通类，犯罪类、悬疑类和恐怖类，可以将喜欢这些类型的用户划分到一个社区簇中。经过分析可以得出，社区簇个数k不会超过10个，并且不会低于3个。因此本文从3～10依次取k的值，通过观察不同的社区簇个数所对应的MAE来确定k的值，实验结果如图2所示。

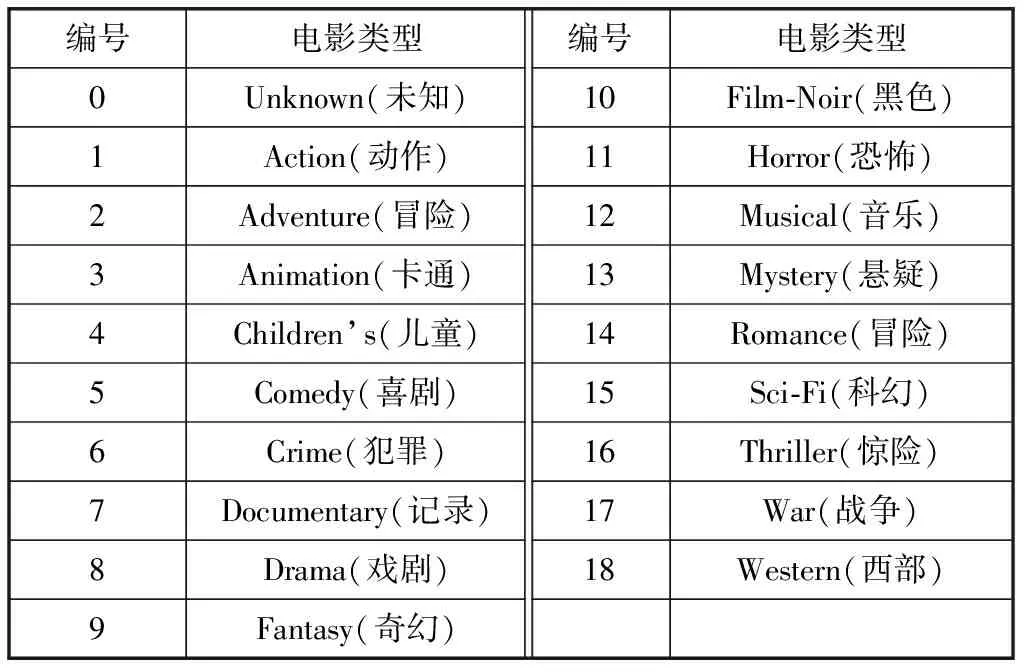
表2 电影类型

图2中u1～u5皆是将原数据集按照80%数据作为训练数据集，另20%数据作为测试数据集进行分割得到的，它们各自有不相交的测试集。从图2可知，当社区簇k为8时，对应的MAE值最小，因此，确定k=8。

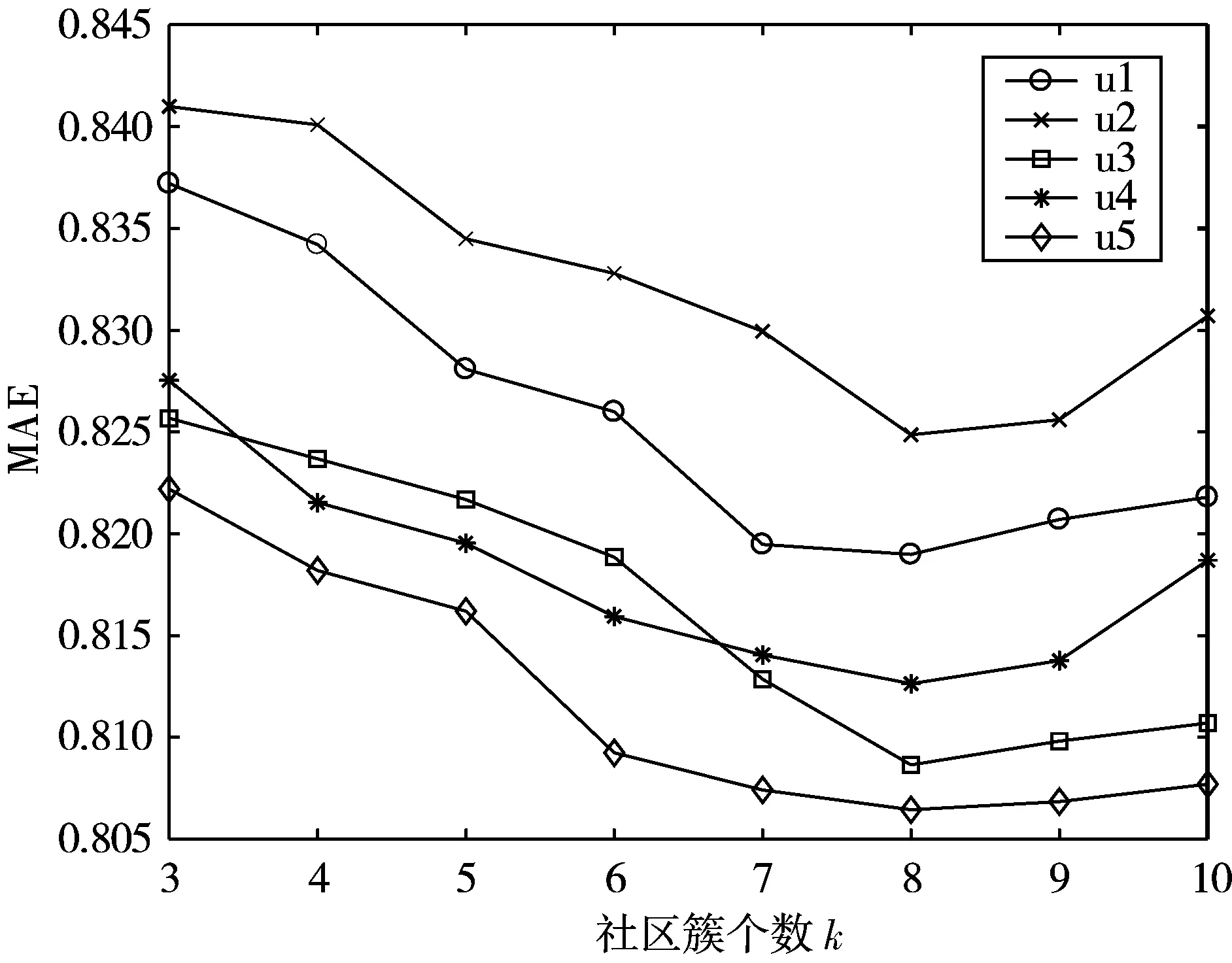
图2 MAE随社区簇个数变化图

2.3.2 确定相似用户数量

相似用户对最终的评分预测起至关重要的作用，如果数量过小，则会丧失许多关键信息；反之，如果数量过多，则有可能将与用户兴趣相反的用户考虑进去，导致评分预测出现较大的误差。因此本文分别将相似用户的数量K取为5、10、15、20、25、30，通过观察相应数量对MAE的影响来决定相似用户的数量，结果如图3所示。当相似用户数量K取值为20时，同时兼顾了较好的MAE值和Precision值，最终确定相似用户数量K=20。

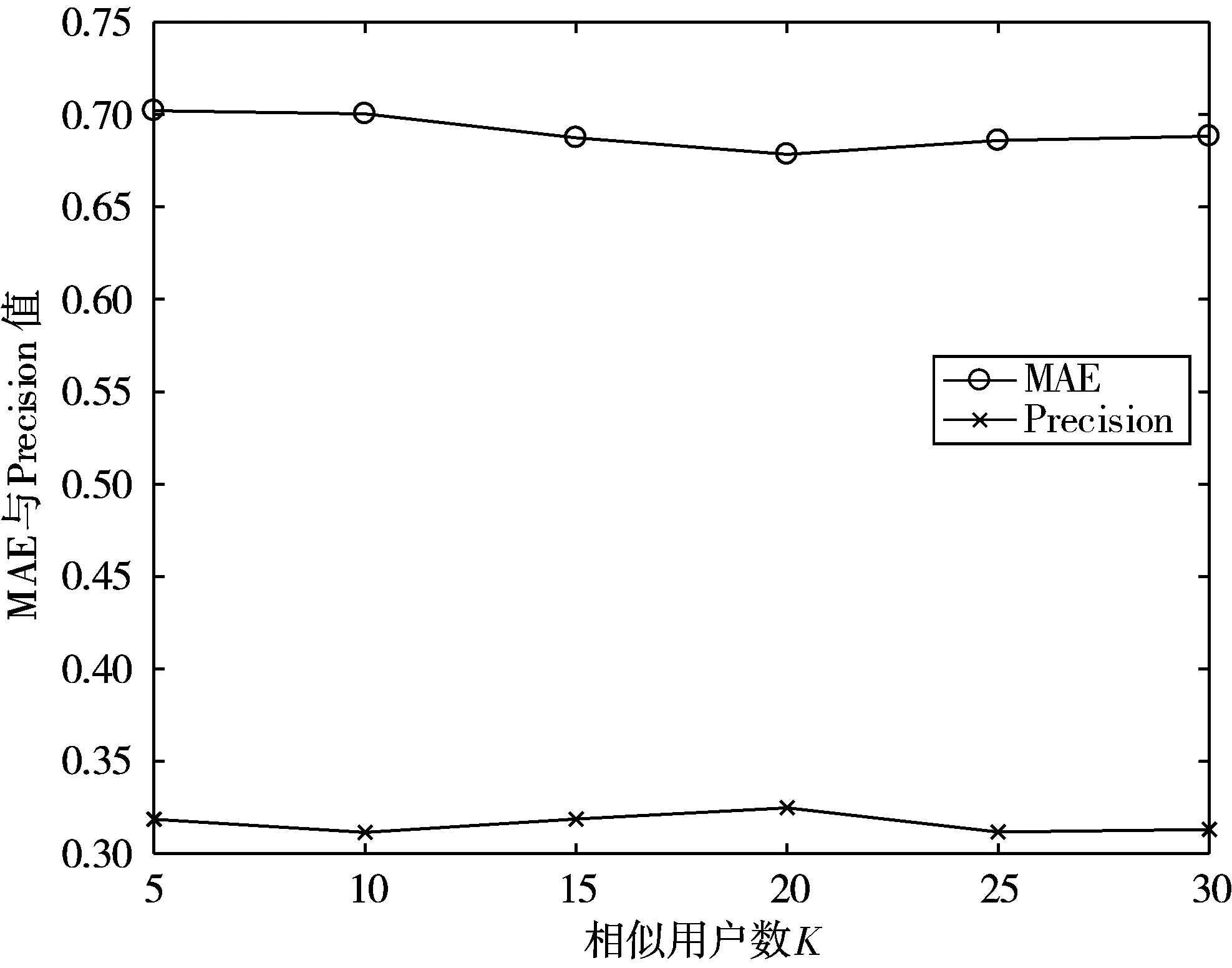
图3 Precision与MAE随相似用户数变化图

2.3.3 确定冷启动问题相关参数

年龄和性别对用户兴趣爱好都有所影响，但其对兴趣爱好的影响程度不同。因此，需要确定年龄和性别的权重平衡因子λ。对冷启动用户进行评分预测时，专家用户与属性相似用户所起的作用也不同。专家用户评分客观，但推荐结果缺乏个性化，属性相似用户则可以弥补个性化方面的不足，但二者权重不同，因此，需要确定出两者的权重平衡因子θ。本文实验数据选用的是MovieLens-100k数据集，将数据集经过8∶2随机抽取3个等量子数据集。将λ和θ从0.1～0.9依次取值，比较本算法在不同λ和θ下的MAE值。经过实验得出，当λ=0.6，θ=0.7时，算法的MAE最小，由此确定2个因子取值。

2.3.4 确定专家比例

根据巴莱特定律，即在任何一组东西中，最重要的只占其中小部分，约为20%，其余80%尽管是多数，却是次要的思想。本文专家用户的比例选取将以20%为中心，从15%～25%中取值，同时评分预测中专家的权重系数α将从0.3逐步增加至0.7，不同参数所对应的MAE的变化如图4所示。

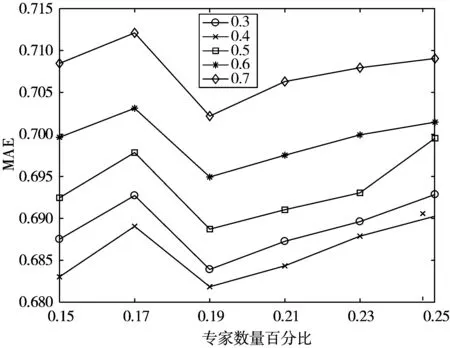
图4 MAE随专家比例变化图

由图4可知，当社区簇中的专家比例为19%时，算法对应的MAE最小。在评分预测公式中，当α取0.4，相似用户所占比例β取0.6时，算法的MAE最小，即用户不仅会听取同社区簇专家，同时还会听取相似用户的意见。综上所述，α=0.4，β=0.6，γ=0.19。

2.4 实验结果及分析

2.4.1 对比实验

为验证本文创新点的有效性。本文将引入以下算法进行对比试验。传统的基于用户的协同过滤推荐算法UCF、文献[16]中的基于专家信任的协同过滤推荐算法EPT、文献[15]中的UCCFRIET、综合用户特征及专家信任的协作过滤推荐算法UCECF[23]及一种带偏置的专家信任推荐算法IBETA[24]进行对比实验。

对比算法在不同相似用户数目K下的MAE值如表3所示，MAE值变化情况如图5所示。

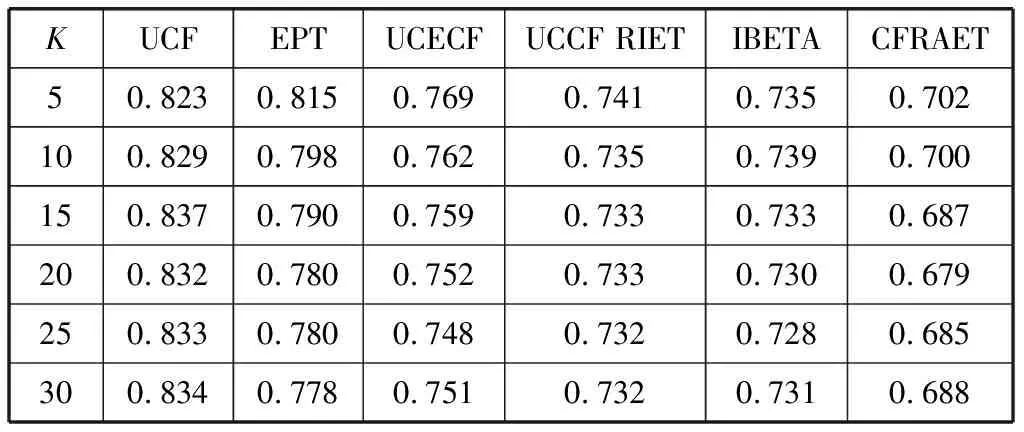
表3 算法在不同相似用户数目下的MAE值

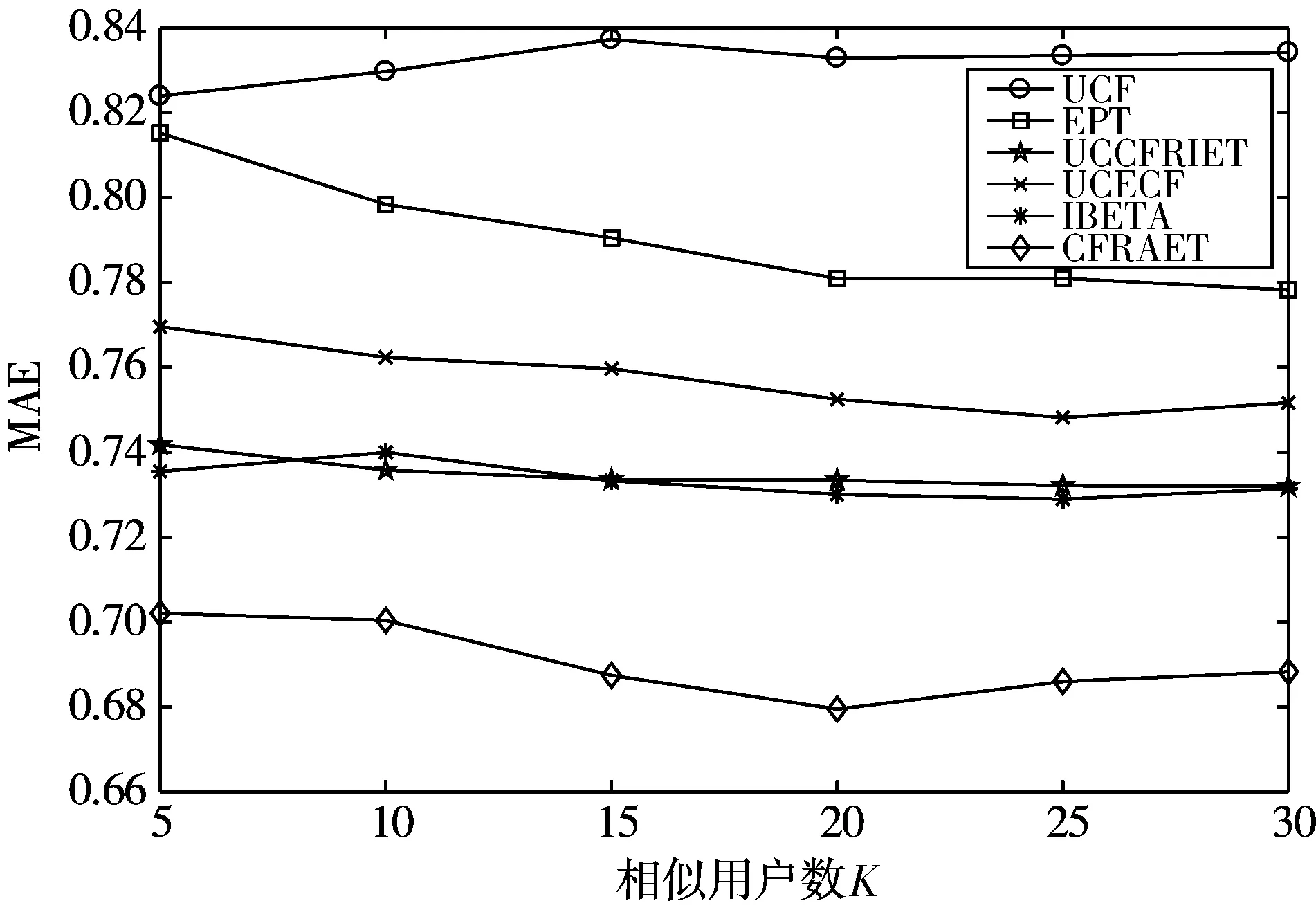
图5 算法在不同相似用户下的MAE变化图

对比算法在不同相似用户数目K下的Precision值如表4所示，Precision值变化情况如图6所示。

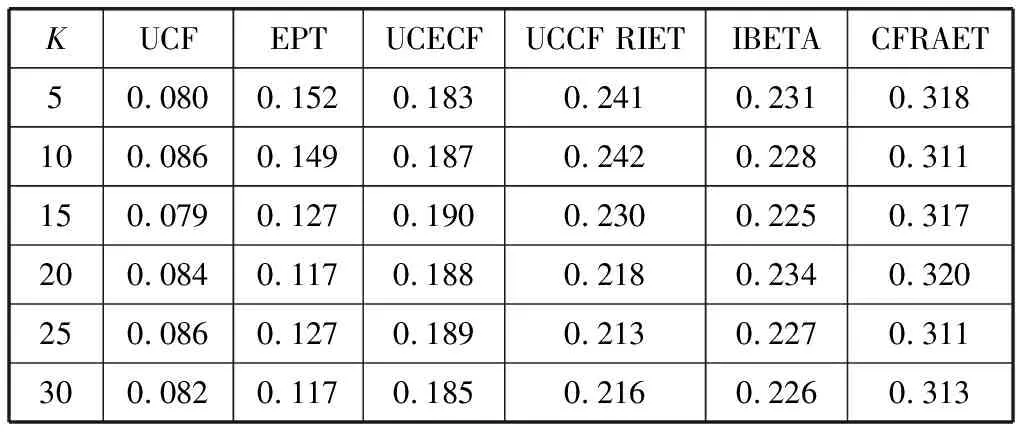
表4 算法在不同相似用户数目下的准确率

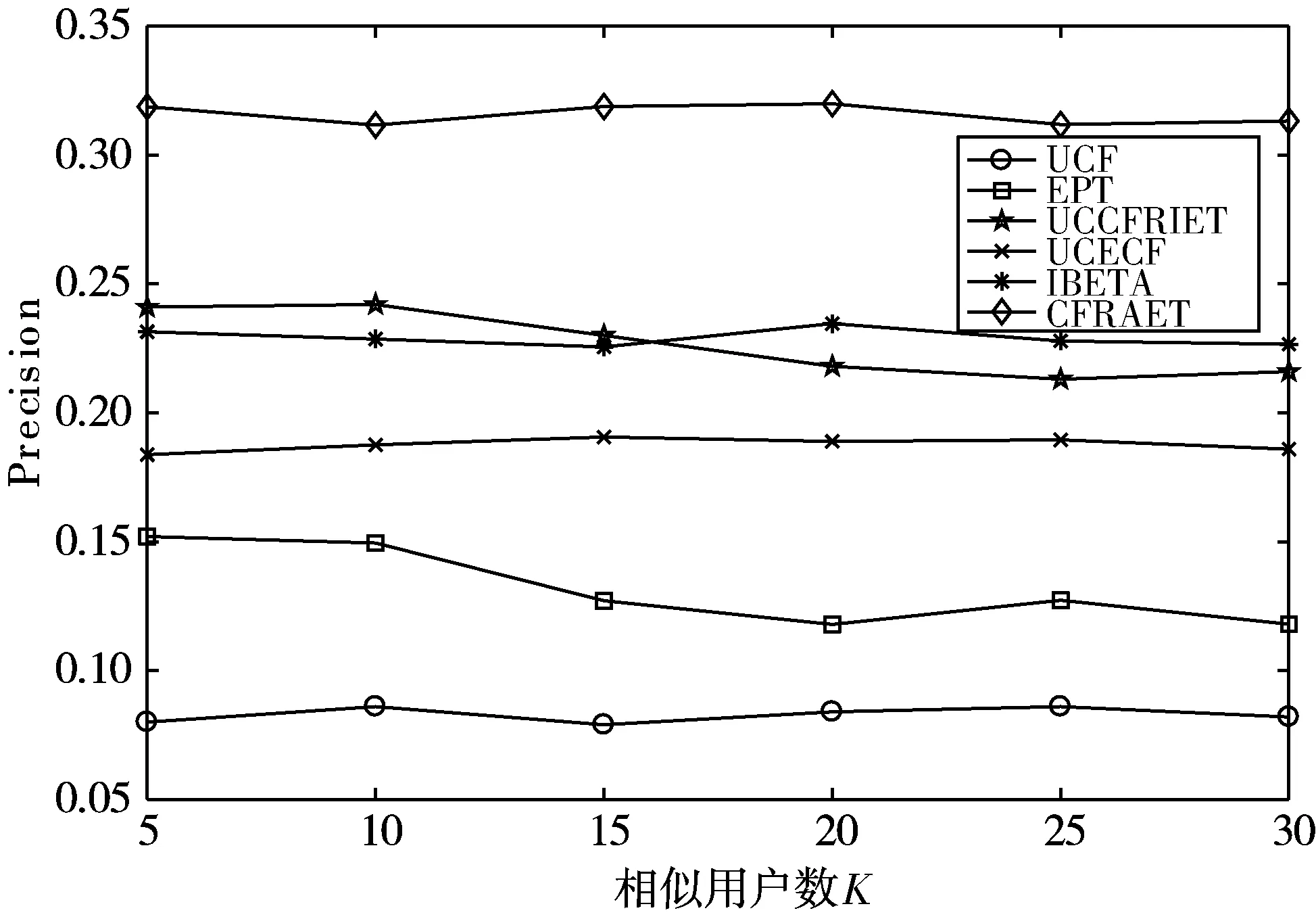
图6 算法在不同相似用户数下准确率变化图

经实验验证，本文提出的算法CFRAET的MAE值最低且Precision值最高。如表3所示，当K=5时，本文算法的MAE值为0.702，小于其他对比算法；在表4中，当K=5时，本文方法Precision为0.318，高于其他对比算法，当K取其他值时，表3和表4也呈现相同结果。综上，本文提出的结合专家信任的协同过滤推荐算法CFRAET在一定程度上均优于传统算法。

2.4.2 通用性证明实验

为验证本文算法的通用性，本文引入了数据集Jester[25]，该数据集包含了73421名用户对100个笑话的评分。该数据集的稀疏度为44.2%。首先是确定实验参数，在Jester数据集中，根据观察不同参数所对应的MAE来确定各个参数，参数取值如表5所示。

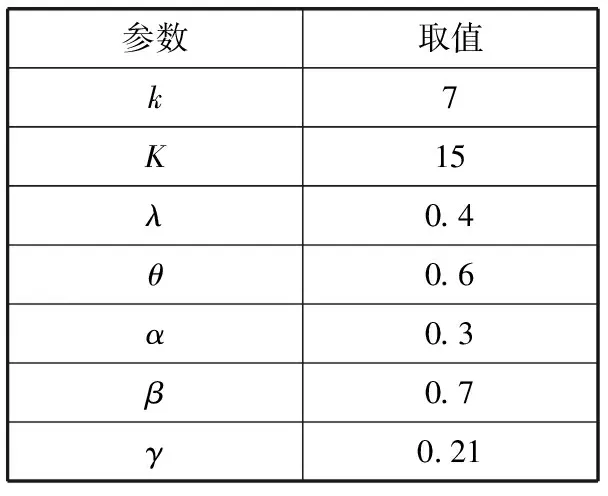
表5 Jester数据集中各参数取值

将表5中的参数代入计算公式中，通过实验得出不同邻居用户下推荐的MAE和Precision值，结果如表6、表7所示。

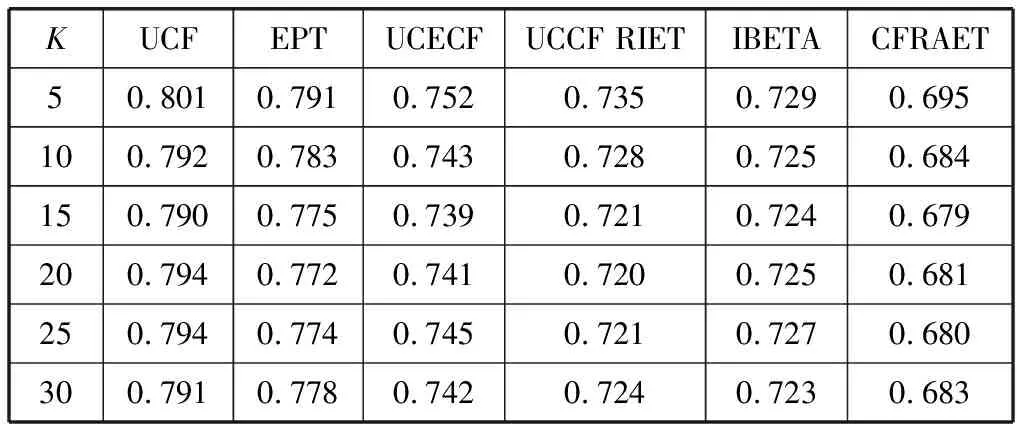
表6 算法在不同相似用户数目下的MAE值

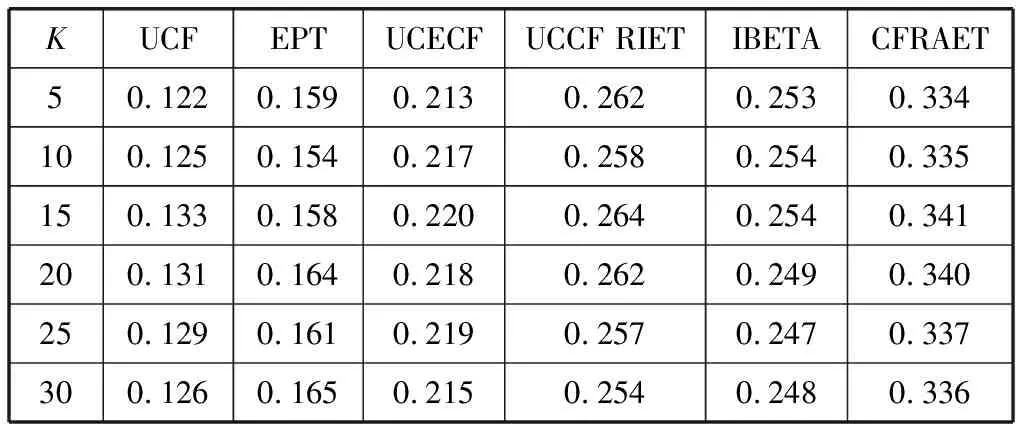
表7 算法在不同相似用户数目下的准确率

通过表6和表7可以看出，本文提出的CFRAET算法在不同领域数据集中仍有良好的表现。如表6、表7所示，与传统的基于用户的协同过滤推荐算法相比较，本文算法MAE降低了11%，Precision提高了20%。综上，验证了本文算法在不同数据集上的效果优于其他算法的同时，也验证了本文算法的通用性。

2.4.3 消融实验

本文通过消融实验进一步验证本文所提出的创新点的效果。为方便对比实验结果，本文设计了以下算法：

1)相似度改进有效验证算法IEVAS(Improved Effective Verification Algorithm of Similarity)。该算法在CFRAET的基础上，将本文的改进相似度部分去掉，相似度计算公式采用公式(1)进行相似度的计算。

2)专家信任度改进有效验证算法IEVAET(Improved Effective Verification Algorithm for Expert Trust)。该算法在CFRAET的基础上，将本文对专家信任度改进的部分去掉，采用公式(11)进行专家信任度的计算。

3)冷启动改进有效验证算法IEVACS(Improved Effective Verification Algorithm for Cold Start)。该算法在CFRAET的基础上，将本文对冷启动用户的预测方式去掉，只采用专家用户为冷启动用户进行推荐。

消融实验的推荐结果如表8、表9所示。

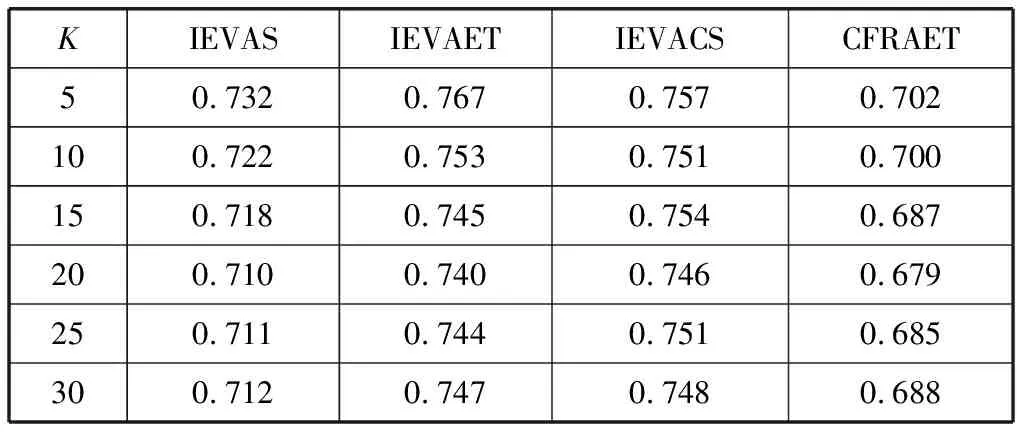
表8 算法在不同相似用户数目下的MAE值

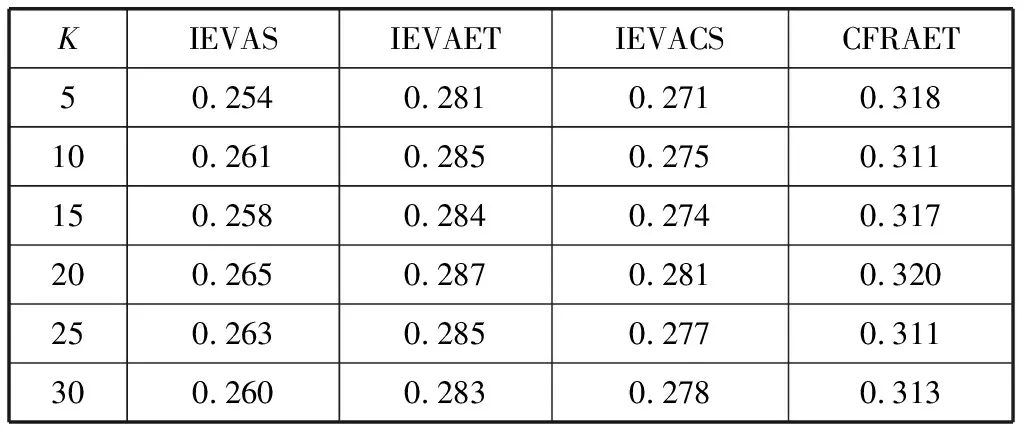
表9 算法在不同相似用户数目下的准确率

通过表8和表9可以看出，本文算法从相似度、专家信任度及缓解冷启动3个方面提出的改进均在一定程度上提高了算法的推荐精度，但3个方面的改进对算法的影响各不相同。如表8和表9所示，当K=5时，在IEVAS、IEVAET、IEVACS这3个算法中，IEVAET算法的MAE最大，Precision值小，说明专家信任度的改进对CFRAET的推荐效果影响最大，其次是冷启动的改进，最后是相似度的改进。当K取其他值时，表8和表9也呈现相同的结果。综上，本文做出的3个方面的改进均提高了算法的推荐精度。

3 结束语

本文针对传统协同过滤推荐算法中相似度计算不准确及冷启动问题，提出了一种结合专家信任的协同过滤推荐算法。该算法在对相似度计算改进中，一方面从用户角度考虑，通过2个用户对同一项目的评分时间所反应出2个用户的隐偏好对相似度计算进行改进；另一方面从项目角度考虑，通过项目冷门因子对相似度计算进行改进。计算专家信任度时，通过时间跨度因子对专家信任度计算公式进行改进。针对用户的冷启动问题，该算法利用社区簇中的专家用户及属性相似的用户共同为目标用户产生推荐。通过实验证明，本文算法的平均绝对误差及准确率均优于传统算法。未来的工作将扩大实验数据集进一步验证算法的有效性，同时注重运用深度学习技术更深层次挖掘用户之间的隐偏好以及影响专家信任的因素。