基于多率采样的MASs在FDI攻击下的安全一致性

贾新春，吕腾，王悦，白文杰

（1.山西大学 自动化与软件学院，山西 太原 030013；2.山西大学 数学科学学院，山西 太原 030006）

0 引言

近年来，由于在各领域的广泛应用，比如多机器人编队［1］，无人车辆控制［2］和电力系统［3］，多智能体系统（MASs）的协同控制受到广泛的关注。在大多数关于连续时间MASs的控制器协议的设计过程中，智能体或系统组件之间的信息传输通常是连续的形式。这种信息传输方式的实施意味着需要充足的通信资源和理想的网络环境。相比于连续形式的控制策略，采样控制策略可以减少计算负担，网络通信资源的消耗以及控制器的更新频率，同时可以确保系统的期望性能。

在过去二十年中，带有采样控制的MASs的一致性控制问题已经被广泛的研究［4-6］。在现存的研究结果中，有两种采样机制广泛的用于多智能系统的一致性控制中：一种是同步采样方法［4-8］，另一种是异步采样方法［9-12］。同步采样意味着通信网络中的智能体以相同的采样周期进行采样，即采样方式相同。与之相反，异步采样意味着不同的智能体采用不同的周期或非周期采样，即智能体不同，其采样方式也不尽相同。例如，文献［5］和［12］分别研究了MASs在同步和异步采样下的一致性跟踪问题。

根据以上关于同步采样或异步采样下MASs一致性研究成果的分析，可以发现现存的同步采样和异步采样机制都包含一个隐含的假设，即单个智能体的所有的输出分量都采用相同的传感器进行采样，即采样周期相同。我们称这样一种采样机制为单速率采样（singlerate sampling，SRS）机制（简称单率采样）。然而，值得注意的是，智能体的输出通常包含多组输出分量，且不同的输出分量通常具有不同的物理特性。此时，采用单一的传感器对输出进行采样已不能满足实际需要，而应该根据输出分量的具体物理特性采用相应的传感器采样。换句话说，就是不同的输出分量要使用不同的传感器以不同的采样周期进行采样。我们称这种采样机制为多速率采样（multi-rate sampling，MRS）机制（简称多率采样）。相比于SRS，MRS有以下优点：（1）MRS可以及时的处理和传输采样数据，且不需要长的等待时间；（2）由于MRS机制下控制器的实时更新性，可以实现更好地控制性能。近年来，对MRS机制研究局限于网络化控制领域［13-17］。最近，文献［18］将MRS机制的研究从网络化领域拓展到了MASs领域，研究了一类异构MASs在MRS机制下的输出一致性问题。然而，对于MRS机制在多智能体领域的研究还有很大的空缺，这激发了本文的研究。众所周知，智能体间的通信可能会存在信息冗余或不必要的信息传输情况，对此，事件触发机制能够减少信息传输次数。近年来，关于事件触发机制的研究已有较多优秀的成果，例如［19-20］。在未来，我们将会在MRS机制的基础上引入事件触发机制来进一步优化网络中的信息交互。

随着网络通信技术的快速发展，网络安全问题在控制领域受到了越来越广泛的关注。众所周知，在MASs中，智能体间的信息交互是在网络中进行的。但是，由于网络的开放性，通信网络极易受到网络攻击的影响，进而影响系统的一致性。一般来说，根据网络攻击的攻击方式可以将攻击分为两种：拒绝服务（denial-ofservice，DoS）攻击和欺骗攻击。DoS攻击通常通过阻断智能体之间或智能体内部通信信道上信号的传输来达到攻击的目的。不同于DoS攻击，欺骗攻击监听并且窜改网络中的真实数据，最终使得接收智能体将窜改后的错误数据当做真实的信号来处理。近年来，针对在DoS攻击或欺骗攻击下MASs的安全一致性研究已有不少的成果［21-24］。例如，文献［21］和［25］分别基于SRS机制研究了在DoS攻击和欺骗攻击下MASs的分布式安全一致性问题。相比之下，欺骗攻击对整个MASs造成的破坏更严重。虚假数据注入（false data injection，FDI）攻击作为欺骗攻击的一种，它通过注入一个干扰数据到真实的数据中，来达到破坏系统一致性的目的。由于这种攻击方式的伪装性，很难被系统检测到。因此，本文致力于研究MASs在FDI攻击下的安全一致性。本文的主要贡献列举如下：（1）不同于DoS攻击下带有SRS的MASs的一致性工作［21-24］，本文解决了在实时的MRS机制和复杂的FDI攻击下MASs的领导跟随安全一致性问题。（2）假设智能体的状态不可得，基于智能体的输出信息提出了一个多率观测器来估计MASs中每个智能体的状态。（3）为了缓解FDI攻击对MASs一致性的影响，提出了一个安全控制协议。它包括一些估计器和控制器，其中估计器可以根据接收到的领导者和邻居智能体的信息估计出智能体收到的FDI攻击。然后，基于估计信息，设计了一个安全控制器来减轻FDI攻击对智能体控制命令的影响，进而确保MASs的一致性性能。

1 基础知识和问题描述

1.1 图理论

定义包含N个跟随者的无向图为G={V，E，A}，其 中 V={1，…，N}，E⊆V×V 和分别表示图G的节点集，边集和邻接矩阵。(j，i)∈E表示节点i可以接收到节点j的信息，且节点j称为节点i的邻居。记节点i的邻居集为。邻接矩阵满足，如果 (j，i)∈E，那么aij=1；否则 aij=0；特别的，aii=0。此外，定义图G的拉普拉斯矩阵为L=D-A，其中D=diag{d1，d2，…，dN}∈RN×N且 di=∑j∈Niaij。定义对 角 矩 阵 G=diag{g1，g2，…，gN}∈RN×N，如 果节点i可以直接收到领导者的信息，则gi=1；否 则 gi=0。 有 向 图{0，1，…，N}和分别表示有向图͂的节点集和边集。显然无向图G是有向图G͂的一个子图。如果从领导者到所有跟随者都存在一条有向路径，则称有向图͂是连通的。定义H=L+G，如果有向图͂是连通的，则H是非奇异的且H的所有特征值都有正实部。

1.2 问题描述

考虑包含一个领导者和N个跟随智能体的线性同构MASs。智能体i(i∈V)的动力学为，

其中xi(t)∈Rn，ui(t)∈Rm和 yi(t)∈Rp分别表示智能体i的状态，控制输入和输出。A∈Rn×n，B∈Rn×m和 C∈Rp×n分别表示适当维度的定常矩阵。且(A，B)是可镇定的，(A，C)是可检测的。领导者的动力学给定为，

其中x0(t)∈Rn，y0(t)∈Rp分别表示领导者的状态和输出。

在本文中，智能体i的输出yi(t)通过MRS机制进行采样。具体的，MRS机制描述如下。输出yi(t)的p个分量根据所选传感器采样频率的不同分为q个子向量。例如，

yiγ(kiγTiγ)表示输出yi(t)的第 γ 个子向量最近的采样信息。假设输出yi(t)有两个子向量yi1(t)和yi2(t)。在图1中给出了一个示例表示子向量yi1(t)，yi2(t)和观测器输出 ŷi(t)采样时刻之间的关系。

图1 对象和观测器的MRS时间序列Fig.1 MRS time sequence of the plant and the observer

注1 多率观测器（3）在形式上和普通的Luenburger相同。事实上，本文根据Luenburger观测器的构造思想，在MRS机制下，基于系统的MRS输出信息作为观测器的输入，构造了多率观测器（3）。与普通Luenburger观测器中使用系统的单率采样输出不同，（3）式中使用的是系统所有输出子向量的整合信息y͂i(t)。其中，观测器的MRS输出和系统的MRS输出通过一个匹配机制［4］实现同步。

1.3 攻击模型

在这部分考虑FDI攻击模型的建立，攻击的目的是破坏MASs的一致性性能。具体地，攻击者实施的FDI攻击过程如下：当智能体将自身的观测器状态广播到网络中时，攻击者从网络中监听和窃取智能体的广播信息。攻击者为了达到欺骗的目的，针对不同的数据，会注入不同的错误数据，具体表示如下：

其中，ηi(tki)表示智能体i广播到网络中的观测器状态，ξi(tki)表示攻击者针对智能体i的观测器状态注入的数据，且它是一个有界信号。(tki)表示网络中被破坏后的信号。

注2 由于智能体间的信息交互是在一个开放的网络上进行的，所以，对于攻击者来说，监听和窃取网络中的数据是十分容易的。因此，在每个智能体将自身的观测器采样信号以广播的方式传输给邻居智能体的过程中，攻击者可以趁机注入一个错误的数据。这样一种攻击方式是合理的。特别的，不同的观测器信号被注入的错误数据是不同的，例如，。 一 般 来 说 ，攻 击 者 的 能 量是有限的，对攻击者来说，注入一个趋近于无限大的信号是不现实的。因此，在本文中，假设攻击信号是未知但有界的。

定义1［26-27］领导者的输出y0(t)关于跟随者i的输出yi(t)是一致最终有界的，如果存在一 个紧 集 J⊂Rp，使得 对 任意的 i∈V，都有yi(t)-y0(t)∈J，即存在一个正实数δ和时刻， 对 ∀t≥t0+tf， 使 得

如果定义1的条件成立，则称所考虑的系统在一致最终有界的意义下可以实现领导跟随安全一致性。

基于上述的分析，针对智能体i安全控制协议设计如下：

图2 带有MRS机制的MASs在FDI攻击下的安全控制框架Fig.2 Secure control framework of MASs with MRS mechanism under FDI attacks

注3 一般来说，在控制器的设计中使用采样信号的开环估计值比直接使用采样信号值的控制效果更好。因此，设计开环估计器（7）和（8）分别来估计从网络中接收到的邻居智能体的观测器状态和攻击信号的连续信息。根据智能体接收的领导者和邻居的信息，式（10）可以估计出攻击者在网络中注入的错误数据。利用（7）—（10），可以建立安全控制器（6）。此外，被攻击者破坏的邻居信号在相应的最近采样时刻更新，在非采样时刻通过（7）—（9）估计。

为了便于后文分析，根据（1）—（5），得到以下闭环系统形式：

在提出主要结果前，对网络拓扑图做以下假设：

2 主要结果

在本节，给出在一致最终有界的意义下，基于MRS机制的同构MASs在FDI攻击下安全一致性的充分条件。

引理1 基于MRS机制的观测器（3）能够估计MAS（1）的状态，如果存在一个正定矩阵P1＞0和矩阵F，使得以下的线性矩阵不等式成立：

定理1 针对基于MRS机制的MAS（1）在FDI攻击下，考虑本文所提的安全控制协议，选择控制器增益K=μBTP。然后，所考虑的系统在一致最终有界的意义下实现安全一致性，如果存在正定矩阵P，Q，正常数α，使得以下的不等式成立，

3 仿真验证

在这部分，给出一个仿真实例验证本文结果的有效性。考虑含有1个领导者和3个跟随者的同构线性领导跟随MAS，领导者和跟随者的动力学如下：

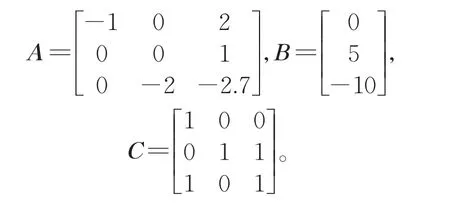
跟随者智能体和领导者之间的通信拓扑如图3所示。在本例中，假设智能体输出由两组子向量组成，记为 yi(t)=[yi1T(t)，yi2T(t)]T，其中yi1(t)∈R2，yi2(t)∈R1。两组传感器的采样周期分别记为T11=T21=T31=0.02s和T12=T22=T32=0.03 s。根据引理1，解得F=［-34.142 5 13.719 8 1.908 8；-1.397 4-0.714 4 2.082 3；57.905 2-30.925 4 0.342 8］。网络中的FDI攻击 分 别 为 ξ1(t)=0.5sin(t)，ξ2(t)=0.5cos(t)和ξ3(t)=0.5sin(t)+0.5cos(t)。显然，攻击是有界的。根据定理1，选择α=0.3，可得到控制器增益

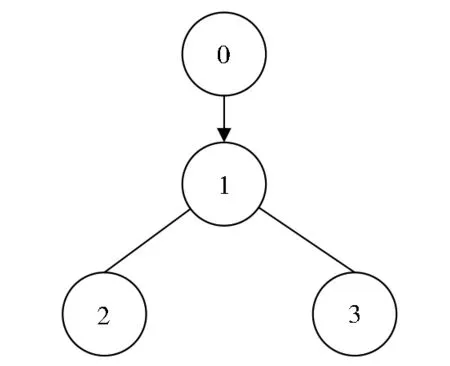
图3 跟随者和领导者之间的通信拓扑Fig.3 Communication topology among followers and leader

K=[0.022 9-0.018 1-0.098 5]。

定义跟随者智能体和领导者之间的输出误差为 ei0(t)=yi(t)-y0(t)，i=1，2，3。然后，跟随者和领导者之间的输出误差如图4所示。可以清晰地看出领导跟随安全一致性在一致最终有界的意义下是可达的。

此外，为了验证本文所提安全控制协议的有效性，考虑控制器中不含攻击信号估计的情况。因此，图5中给出在一般传统控制协议下，跟随智能体和领导者之间的输出误差演化轨迹。通过比较图4和图5，可以明显地看出在本文所提的安全控制协议下的领导跟随一致性性能优于传统控制协议。综上所述，称基于MRS机制的MASs在FDI攻击下，使用本文所提的安全控制协议可以明显地缓解攻击对系统一致性的负面影响。

图4 跟随者和领导者在安全控制协议下的误差轨迹Fig.4 Error trajectories among the followers and the leader under the secure control protocol

图5 跟随者和领导者在没有攻击信号估计的控制协议下的误差轨迹Fig.5 Error trajectories among the followers and the leader under the control protocol without attacks' estimation

4 结论

在本文中，我们研究了基于MRS机制的MASs在FDI攻击下的一致性问题。在智能体的状态不可获得情况下，考虑基于MRS输出信息，设计了一个多率观测器来估计智能体的状态。然后，提出了一个安全控制协议，确保了所考虑的系统在一致最终有界的意义下实现领导跟随安全一致性。在未来，我们将研究带有MRS机制的MASs在更加复杂的网络攻击下的安全一致性问题。