网络计量学和替代计量学的挑战及其社会影响的稳健和非稳健计量评价

刘廷元，刘纾曼

（西南石油大学图书馆，成都 610500）

1 引言

科学成果的社会影响评价是广义科学成果评价的一部分。传统形式的狭义科学成果评价主要是建立在文献计量学、科学计量学的期刊引文指标之上，以学术影响测度为主。新兴形式的广义科学成果评价，将其扩展到网络计量学、替代计量学的关注-使用指标之上，以社会影响测度为主。

目前，基于网络计量学（webometrics）、替代计量学（altmetrics）的科学成果计量，到底是选择学术影响还是社会影响的路径，不同学者有不同的观点和认识。altmetrics一词的创立者Priem等[1-2]认为，应当选择“基于在线工具及环境活动的学术影响计量”路径，重点关注Twitter和Facebook等社交媒体上的转载数据。Priem[3]对altmetrics的定义，不但将学术影响包含在不断变化的工具和数据聚合环境活动中，而且还包含了将其定位为网络计量学的一个分支。

然而，由于网络计量学、替代计量学的影响计量与传统形式的影响计量存在较大差异，有的甚至不相关，导致影响的内涵及其计量方法备受争议[4-5]。altmetrics或alternative metrics术语中的“替代”即“alt(ernative)”也经常受到批评，因为大多数实证研究都表明，替代计量学视角下的影响与传统计量形式的影响相比，不但相关性很弱而且可靠性和稳定性也没有得到很好解决，只能被视为一种补充而不是“替代”。这就导致一些学者将学术引文指标和社交媒体指标从总括性的影响术语中分解出来[6-7]，将它们定义为相互补充而不是相互替代的影响研究，即所谓的学术维度和社会维度[8-9]。而另外一些学者，则只将影响看作文化或社会方面的共鸣，即影响不再被视为科学成果学术质量的代表，而是在更广的意义上被定义和使用[10]。因此，用于分析和提供科学影响数据的网络计量学和替代计量学，也被定义为“基于社会网络的新指标的创建和研究”[11]。

对于网络计量而言，Ingwersen[12]提议采用类似于引文分析的网络影响因子（web impact factor，WIF；包括外链数、内链数和总链数指标）来计算社会网络的影响，并将网络计量学定义为研究网络信息资源、结构和技术的构建与使用的定量方面[13]。然而，社会网络影响的复杂性大大超过了多源数据计量的相对简单的信息计量方法，使传统的网络计量很难对多种网络的深层使用信息（如情境数据）进行统一的分析、评价，需要建立一种以多源数据聚合为目标的新计量框架。经过Adie等[11]的研究，特别是多种网络和社交平台的关注-使用指标的创建，提出一种通过提及、推荐、共享、收藏等指标进行加权计数的“altmetric关注分数”（at‐tention score）来计算社会网络的影响。对于替代计量而言，Adie及其合作者Roe等提出的“altmetric关注分数”和“altmetric分数”，成功地结合情境指标数据，如作者、内容、情感等，对研究成果的各种社会影响进行深层计量评价[11]。一般而言，论文、论著的在线讨论、分享、收藏等关注-使用越多，指标的权重越大，altmetric分数越高。因而，从维度和质量上看，替代计量的社会影响分析比之前的其他任何一种计量都更复杂。因为替代计量的来源数据及其权重都具有主观成分，更重要的是，它还存在多种维度的局限和缺陷，例如，普遍存在计数/分数为0，以及因为涉及利益相关者，普遍存在原始计数的多种不规则性，从而使原始数据对一些成果的影响评价几乎没有什么区分能力，对成果的评估任务也没有什么用处[14]，计量评价的可靠性和稳定性难度大大增加。

尽管替代计量具有许多局限和缺陷，但替代计量指标的丰富情境远比网络计量指标的单纯计数能给人更多的启发。按Björneborn等[13]的解释，网络计量是超链接的数量和类型、万维网的结构和使用模式的计量，它可以告诉我们，某个网站从其他网站接收链接的网页数量与该网站发布的可供访问的网页数量，即表层使用频率的网络影响因子[12]或其他社会影响因子等。替代计量则是来自各种网站接收访问的非常多样化的网络关注-使用数量的计量，它可以告诉我们网站发布的网页（研究成果及其论文、论著）在社会网络中具体应用的传播数量，即深层使用频率的altmetric分数[11]或社交媒体指数（social media index）等[15]。因此，替代计量是对表层网络使用信息的深层应用分析，是对网络计量的更大补充和发展，二者不是两个完全不同或对立的信息计量分析体系。网络计量和替代计量是广义信息计量学发展的两个必然阶段，本质上属于一个统一的网络信息分析整体，即一个统一的广义信息计量学分支。基于此，二者可以并称为网络-替代计量或网络-替代计量学。

在本研究中，我们对网络环境下国家社会科学基金（简称“国家社科基金”）项目成果的社会影响数据进行了广泛采集和分析，特别关注网络-替代计量指标数据和计量评价的稳健性。这里，重要而又不能回避的问题是，网络-替代计量指标数据本身存在多种不确定和不完备的局限或缺陷，尤其是高零值（左侧）、多异常值（右侧）和极端右偏斜分布之间的复杂关系，以及由此带来的计量敏感和失效风险，使社会影响的计量评价在数据、方法和结果等方面都面临巨大挑战。解决这些问题的基本思路是利用稳健计量方法消除或削弱高零值、多异常值和极端右偏斜分布对一般信息计量和中心信息计量分布趋势的干扰，即通过四分位零值缩减法进行抗差性检定（左），通过缩尾求稳方法进行异常值合理修正（右），以及通过缩尾均值对偏斜分布数据进行稳健的无量纲化和综合评价。由于传统回归模型是基于信息计量分布的正态性（对称性）和规则性（均匀性）假设，对数据普遍存在的计数为0（非对称性）及其他不规则性外围和异常子群（异常值或对称/非对称轻尾/重尾）高度敏感[16]，信息计量模型及其数据拟合的抗差性、可靠性和稳定性都不高。因此我们将对数据集的非正态不规则分布外围及其异常子群不具有抗差性、可靠性和稳定性或抵抗作用的一般计量方法，称为非稳健计量；将对数据集的非正态不规则分布外围及其异常子群具有抗差性、可靠性和稳定性或抵抗作用的有效计量方法，尤其是对零膨胀（高零值）、多异常值（高杠杆）、极端右偏斜（重尾）和污染数据具有抵抗作用的计量方法，称为稳健计量。

在此方法基础上，以四川省2005—2014年验收通过的341项国家社科基金项目成果的社会影响数据，应用稳健的计量评价方法进行实证研究。需要说明的是，因国外网络和社交媒体中的国家社科基金项目成果数据较少，且与国内数据的相关性较差，本研究未予以采集；社会影响的时间累积效应因素，因需要专门的时序动态响应计量方法也未涉及。

2 网络计量学和替代计量学的社会影响评价挑战

对于以网络-替代计量指标数据为基础的社会影响评价而言，最重要而又不能回避的挑战是原始数据集的不确定和不完备缺陷；尤其是高零值（左侧）、多异常值（右侧）和极端右偏斜分布及其非稳健方法可能带来的计量失效风险，已经大大超过了早期信息计量学在指标创建和研究时遇到的“测度恶魔”：随机性、模糊性和显著歧义性[17]。以网络计量学和替代计量学为代表的现代信息计量学试图将科学成果的社会影响评价，搭建在一种多维度的网络信息活动上，并以丰富的网络关注-使用指标数据来测度科学的社会影响。然而，网络环境下的社会影响计量，涉及不同的利益相关者和技术平台，数据产生、使用和扩散的动机、行为高度复杂，要实现真实、合理和公正的反映，如科学成果在网络上的关注、使用、下载、分享、提及、阅读、评论等指标，达到类似于传统引文学术影响的抗差性、可靠性和稳定性，首先面临两大挑战。

2.1 左侧挑战：高零值和零膨胀分布

对于社会影响计量来说，可用网络-替代数据集的高零值（即“低覆盖”，信息计量学者习惯用“覆盖率”代替“零值率”）问题是一个非常独特的重大挑战。由于低零值意味着置信区间即使是保守的、稳健的，也能覆盖真实参数[18]。相反，在高零值分布下，样本的置信区间即使是保守的、稳健的，也会对数据集的真实性、合理性及其分布偏差和误差造成很大影响，从而大大减少或削弱信息计量方法和结果的抗差性。

零值率等于1减去覆盖率之差，对覆盖率的定义一定意义上也是零值率的定义。对于覆盖率，信息计量学有两种不同的角度。Haustein等[19]从“有”的角度出发，将覆盖率定义为：特定平台上至少有一个提及的文档的百分比；Thelwall[20]从“无”的角度出发，将覆盖率定义为：无零值的产出比例。无论从何种角度定义，覆盖率都绕不开“零值率”，因为高覆盖率意味着“0”值低（少），低覆盖率意味着“0”值高（多）。

Mas-Bleda等[21]对西班牙和英国8个学科的调查结果显示，网络-替代数据中Mendeley的覆盖率最高，80%的抽样文章拥有一个或多个Mendeley读者，其次是Twitter（34%），其余来源的覆盖率则低于3%。许多跟踪调查发现，一些科学成果在提及和社交媒体中能追踪到的信号数量很少或几乎不存在，具体的实践中也存在同样的困难[22]。Sugimoto等[23]在综述中提到Gorraiz等人的4篇文献调查结果，发现F1000的覆盖率研究相对较少，已有的覆盖率调查从小于1%到2%～8%不等。Glänzel等[24]发现，在公共卫生领域的12项指标中，零值率的比例最高的达到78.7%（捕获），最低的为1.4%（提及），大多数则接近50%。Chi等[22]指出，在自然科学中，与生命科学或社会科学相比，这些指标类别的覆盖率或数据可用性的百分比还要低。

社会影响指标变量中的高零值，使数据集中心部分的左侧产生大量的无影响数据。零值率超过50%时，会形成严重的零膨胀（zero-inflated）分布，导致有影响的信息计量分布向右过度偏斜，使高零值下的影响计量面临一般信息计量和中心信息计量分布的抗差性和一致性大大减少或削弱的挑战。从多指标变量的“严密分析”角度看，高零值不能全截断，也不宜随意切尾或删除，因为每个变量的零值率、偏度不同，单侧分位点意义也不同，样本的置信区间及其结构信息含义也不同。

2.2 右侧挑战：多异常值和极端右偏斜分布

与传统的学术影响指标相比，社会影响指标的计数和分数更容易受到人为干扰，被个人、机构及其自动账户（机器人）操纵，产生网络-替代数据的作弊即蓄意污染；尤其是在科学成果的社会影响成为评价指标之后，一些行为不端者、中介、商业机构出于相关利益驱使、游戏化（遵循坎贝尔定律）及恶意心理，会试图通过某些数据点的超级放大（极端异常值）来提高或破坏科学相关者的影响地位。对社会影响的异常子群即多异常值，如果全截断或部分切尾/删除，信息计量的完整性会受到潜在威胁；但如果全保留，就会使一般信息计量和中心信息计量的分布趋势发生潜在扭曲[25]。因而，多异常值和极端右偏斜分布，会对数据集的真实性、合理性及其计量方法和结果的可靠性与稳定性造成严重影响或损害，从而给计量评价的稳健性带来巨大挑战。

此外，由于网络-替代数据的来源、内容、标识、粒度、精度及其学科覆盖并不十分清晰和确定，或者数据调查者和分析者的质量保证与科学能力不足，未能进行严格、规范和统一的技术性控制，给数量众多的多源数据的挖掘、聚合、清洗、提取、检测等带来诸多技术疏漏，本身也容易产生数据的高意外污染，出现系统性异常子群，或大量的零值、缺失值、错误值。因而，数据处理技术的可靠性和稳定性也会对计量数据的分布及其真实性、合理性造成严重影响或损害，有时甚至成为一种关键挑战。

就前者而言，蓄意污染会直接导致数据集的均值、极大值偏高或超高，以致出现杠杆性污染；就后者而言，意外污染则直接导致指标值的均值、标准差和方差的不真实或不稳定，以致出现系统性污染。所以，数据集的右侧不论是蓄意污染还是意外污染，都会给社会影响的真实性、合理性及其信息计量方法的可靠性和稳定性带来诸多问题；因为远离中心或偏离一般分布模式的多异常值，一旦出现在指标数据集中，如果不采取可靠的稳健计量方法，就会使评价模型产生坏解，导致非正态不规则分布外围及其异常子群计量出现高度偏差和误差。理论和实证研究很容易证明，在非稳健模型中，即使一个孤立点也会对数据集产生扭曲性的影响。

由于一般计量数据普遍存在的信息计量分布特征也是右偏态分布，网络-替代计量指标中的多异常值，会将这种向右偏斜的不对称特征进一步放大，并与数据集左侧的零膨胀分布共同作用，将这种过度右偏斜的不对称特征超级放大，从而成为极端右偏斜分布，使社会影响的计量面临更大的挑战。

3 网络计量学和替代计量学的稳健方法

对于以指标观测数据为对象的计量学来说，高零值和多异常值在什么条件下是“真实的”（true），可以作为样本值进行合理的保留或修正，在什么条件下是“过度的”（extra），只能作为结构值，即一定条件下对“结构性（真实）零”[26]进行适度的截断或隐匿，是现代信息计量学发展的重要基础。30年前，加拿大学者Tague-Sutcliffe[27]在纪念情报学家布鲁克斯（Brookes）的文章中说，Brookes曾对等级模型中的长尾（long tails）隐匿感到非常不解，因为用大小-频率方法将长尾全截断（隐匿）过于简单，存在严重的结构信息丢失。这个问题一直到“五计学”的今天，仍未彻底解决。例如，在信息计量学的研究中，普遍调查分析网络-替代指标的低覆盖（基于学科、主题、地区等）[19-23]，却不对已经产生的高零值计量困境进行实质性的数理分析；普遍调查分析指标无零值的密度[28-29]，却不对指标有零值的强度进行关联性的计量评价。后者本应该与前者并列，但在这些文献中都不提及。显然，在覆盖率和密度的研究中，已有文献对零值、近零值及其长尾分布，其实是在进行结构性的截断或隐匿，尽管大都是无意识的。然而，当来源数据普遍存在零过多、异常值和过度离散时，即使样本的置信区间是保守的、稳健的，信息计量分布及其异常值检测的抗差性也会大大降低或不具有抗差性，这时如果进行样本性全保留或结构性全截断，都会给计量评价造成极大损害。在数理统计及相关研究中，通常基于零膨胀模型，把零值看作“真实的”和“过度的”两个不同质的群组，即分为零计数和非零计数两个子集，从总体混合概率分布上进行研究[30]。然而，如果数据集存在多异常值，基于不同计数模型的混合概率必然受到影响，其“真实的零值”和“过度的零值”拟合数据也不可靠。因此，网络计量学和替代计量学在研究高零值、异常值和极端右偏斜分布时，必须在信息计量分布的保留、截断或修正、隐匿的条件和方法上找到自己的科学起点和出路。

3.1 基于左侧高零值和零膨胀分布的稳健方法

信息计量学的大多数原始数据集，并不满足异常值识别的先验假设：正态性、规则性。如上文所述左侧挑战[24]及相关文献[31-32]中报道，许多指标数据集的零值率（Zr）在50%左右，即使不考虑右侧多异常值，也是典型的零膨胀过度右偏斜分布。以异常值检测抗差性较好的四分位法为例，当Zr在75%左右时，是典型的零膨胀极端右偏斜分布，它直接导致Q3=Q1=0即四分位距（inter-quartile range，IQR）等于0，或接近于0，样本箱线图的图框中线将不起作用，观测值的IQR检测完全失效即检测不出异常值。另外，零膨胀产生的非均匀右偏斜分布，还使最终的多指标综合评价很容易受到异常值的干扰。由于零膨胀对中高分位的下限和上限影响很大，因此，原始数据集左侧的抗差性检定对异常值的识别和修正非常重要。

如果数据集的Zr＜25%，即Q1＞0，根据统计学的样本置信区间理论和零膨胀样本结构理论，数据样本的抗差性较好，低分位零值可以作为“样本性零”保留，尽管其中也可能有非真实的零，但因危险率小可以忽略，因此低分位零值的保留系数为1（4/4），使其具有样本性。但如果数据集Zr≥25%，其中有较大比例的非真实的零，数据集的抗差性降低或不具有抗差性，零值可以作为“结构性零”适度隐匿，在Q2＞0或Q3＞0处左截断，但不完全删失，仅在Q3-Q1＞0处等效地观察满足异常值检测的条件，保留一定比例的零值，使其具有等级结构性。因为零值并不是缺失值，在本研究中只是暂时未产生社会影响的观测值，是一个随时可能苏醒的科学“睡美人”，它的存在有计量意义，将所有的零值删失或隐匿会导致信息严重丢失。因此，依据不同数据集的零值长度即Zr，在满足Q3-Q1＞0的条件下，均匀性缩减数据集的零值，既可以保证每个数据集的异常值检测的一致性和抗差性，也可以保留数据集之间的原始信息差异，同时可以观察数据集左侧齐性和右侧异质性对异常值的影响。由于四分位Zr≥75%，异常值无法检测，因此，高零值条件下Zr的缩减率≥0.25是四分位异常值识别的充要条件。

异常值识别前数据集左侧的抗差性处理，可以采用满足一致性控制要求的四分位零值率（Qr）进行自适应零调整。其中，零值率的分位数定义为Q1、Q2、Q3、Q4四个分位；零值的分位保留系数定义为四个等级结构：1（4/4）、3/4、1/2（2/4）、1/4；四分位零值率定义为四个区间的分段控制函数及其缩减的值域。从以上定义及其三者之间的关系，可以推导出以下定理和引理。

定理2.在四分位数据集中，若Zr的分位越低，则Qr越低，Qr缩减的值域也越低；若Zr的分位越高，则Qr越高，Qr缩减的值域也越高。

引理1.Qr缩减的初始值域等于0，即Q2最小Zr与Q2下限的Qr之差等于0；Qr缩减的最大值域等于一个临界值，即Q4最大Zr与Q4上限的Qr之差渐进于常数0.375。

显然，四分位零值缩减法就是通过变量求Zr与Qr之差。依定理1，四分位零值率的分段控制函数为

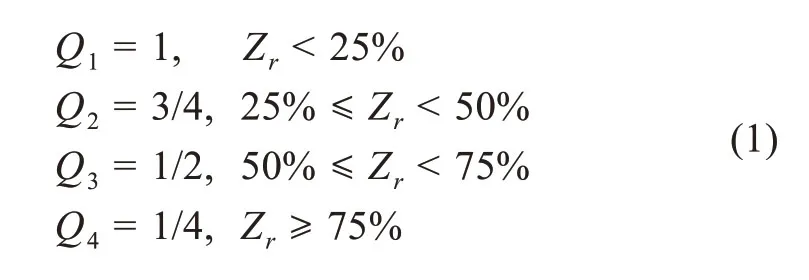
因为公式(1)中分段函数的斜率不一致，低分位上限和高分位下限的端点间等级下降速度不均匀，所以用端点空白值作线性回归的Y轴截距，进行一致性逼近校正，依定理2，四分位零值率的精确计算公式为

公式(2)中，Qr缩减的最小值域等于0，最大值域渐进于常数0.375，引理1得证。

由于截距是等级下降速度的0.25/4或相应的倍率，用公式(2)计算，一致性准确率达到98.81%，回归标准误差为0.0207。公式(2)中，Qr在各分位区间段上单调递增，在所有分位也单调递增且连续，分段函数实现平滑衔接。

3.2 基于右侧多异常值和极端右偏斜分布的稳健方法

计量评价研究的主要目的是多源信息评价，通常意义上也称为多指标综合评价。不管综合评价或信息聚合采用何种方法，包括加权还是不加权、线性还是非线性、奖励还是惩罚、标准化/无量纲化还是近似算子，都离不开均值、最大值等中间和右侧数据的耐抗性和可靠性。因为来源数据一旦存在多异常值和极端右偏斜分布，必然会使均值、最大值、标准差等变量发生扭曲，从而对映射、标准化/无量纲化或算法的耐抗性和可靠性产生影响。

对线性比例的均值化法而言，信息计量学和统计学具有耐抗性和可靠性的方法主要有以下几种。

（1）切尾均值（trimmed mean，TM）。假设X1≤X2≤…≤Xn样本容量为n的顺序观测值，称每侧切除t个观测值再计算剩余数据集的均值，为数据分布1-α中心部分的切尾均值[33]，

(5)实训环节的设计：中职、高职院校非常重视实训教学，克服困难到在建项目施工现场进行教学，但是由于交通问题、安全问题、在建项目选择等问题，大部分课堂教学、实训环节仍在校内完成。校内实训基地建设时追求观赏性、展示性，甚至试图真实再现施工现场，不屑让学生参与砌墙、抹灰、墙砖镶贴等最基本的工作，实训教学时流于形式，学生真正动手操作的环节不足，难以达到预期的效果。中职阶段，应该重视学生的操作和动手能力，例如墙面砖镶贴时，只通过视频、幻灯片来展示其施工过程，学生只能掌握基本的工艺流程，如果让学生动手完成墙砖镶贴的全过程，这样更能吸引学生的兴趣。

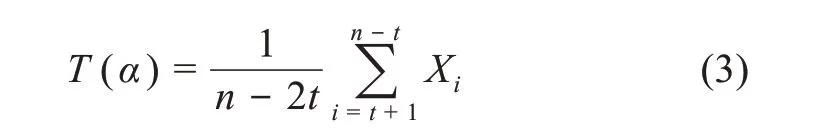
其中，α为切尾率，α=(t/n)×100%。

显然，αn/2观测值要从每侧移除。特别地，当α=0%时，切尾均值就是均值；当α=50%时，即左右两侧各切除大约50%，仅保留中间顺序观测值（n为奇数时保留一个，n为偶数时保留两个），将其余顺序观测值全部切除，切尾均值就是中值。由于α切尾均值的崩溃点是α/2，随着区间α值的增加，α切尾均值的耐抗性和可靠性将更加稳健。当其崩溃点为0时，均值可以被一个孤立点扭曲，说明均值极不稳健。

切尾均值未丢弃数据集中间的大部分信息，能有效地抵抗或消除左右侧异常值（或离群值）及局部偏斜的影响，从而更稳健地反映数据总体的平均水平。此外，若数据集是正态分布，则均值和切尾均值将是相同的。

（2）缩尾均值。缩尾均值是通过将异常值（或极值）替换为某些百分位的数据来确定的，这为所有统计分析提供了一个合理的集中趋势表示[34]。它基于对数据进行排序，将最低α×100%和最高α×100%互变模拟值和观测值，并将异常观测值替换为边界值X([αn])和X([(1-α)n])最接近的模拟值，根据试验的极值分配权重。用方程式描述缩尾均值Wα为

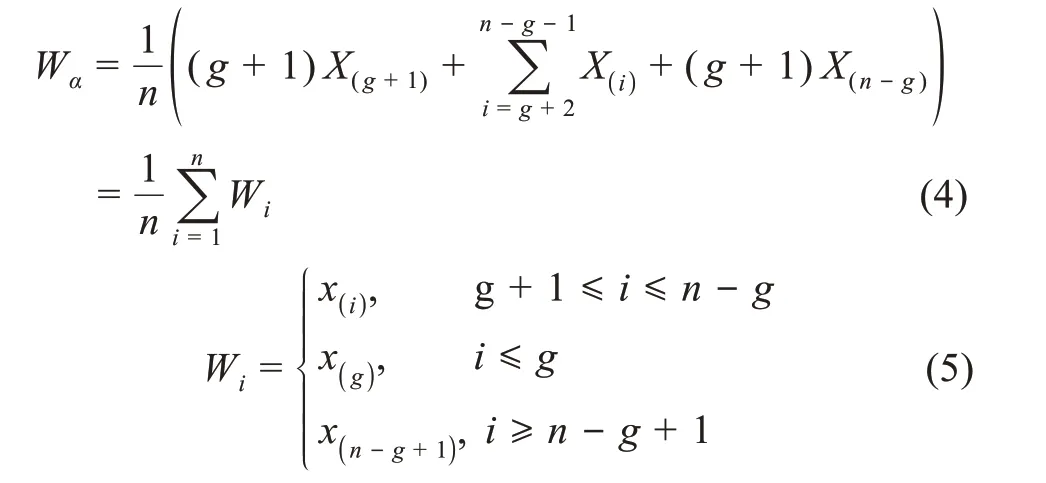
其中，g=[an]，g最大整数≤an，a表示最大允许估计误差，n表示观测数。

异常值的切尾或截断的做法对耐抗性和可靠性是有帮助的，但会因集中在均值上而受到损害，导致样本大小变化和边界丢失。相反，像缩尾值这样的稳健估计方法，可以用于缩尾修正，保留数据中心和两侧的重要信息。缩尾值修正估计量通常比未经筛选的估计量对异常值更具耐抗性和可靠性，因而，缩尾均值是样本均值的一个很好的替代选择。缩尾修正计量比切尾修正计量在技术上有更大的优势：①用最接近异常值的位置替换或交换异常值；②数据的样本大小保持不变；③有助于防止边界信息丢失。

（3）MOM（modified one step M-estimator）和WMOM（winsorized modified one step M-estimator）。作为切尾均值和缩尾均值更好的替代品，推荐MOM（修正的一步M-估计量）和WMOM（缩尾修正的一步M-估计量），它可作为异常值出现时数据分布修正的估计量。

（4）缩序均值。它是一种基于缩序值的具有保留原始信息大小（序）关系的均值估计方法。多异常值的缩序计量方法与应用将另文研究。

4 网络-替代计量指标数据的分类及其稳健计量方法

本研究的原始数据集来源于四川省2005—2014年的341项国家社科基金项目成果（专著类）的网络-替代计量数据采集样本，样本总数683190件。其中，单一来源596269件（中国知网），精确匹配样本事件数596261件，召回的精确率达到99.99%，采集数据的密度为2114.43件，强度为1748.59件；多源大数据86921件，精确匹配样本事件数23121件，召回的精确率为26.60%，采集数据的密度为255.65件，强度为187.10件，表明指标数据具有一定的有效性和可靠性。具体的数据采集步骤、方法和结果见作者另文。

4.1 网络-替代计量指标的分级-分类

由于越来越多的科学成果通过互联网和社交媒体进行交流，用来评价其社会影响的网络-替代指标也越来越多。根据国外学者和Altmetric.com、Plum Analytics等平台应用[31-32,35-36]，社会影响评价的一级指标一般包括使用（usage）、引用（cita‐tion）、社交媒体（social media）、提及（mention）和获取（capture）。其中，使用包括点击、下载、浏览、图书馆藏书、视频播放，引用包括引文索引、临床引用、专利引用、政策引用等，社交媒体包括访问量、点赞、分享、推文，提及包括博客帖子、评论、综述、维基百科、新闻媒体，获取包括书签、交叉编码、收藏、读者数和观众数[36]。从理论角度看，网络-替代计量指标的分级-分类涉及指标特征属性的信息差异和相似性，如何区分或聚合面临很大困难；从实际的操作角度看，没有一个包容性的计量指标框架，网络-替代计量会很困难。本研究基于社会影响指标的属性重要性，以及组内和组间的相似、差异关系，数据位置和尺度的稳定性，同时考虑国内多源数据的易获取性，将社会影响（相对于传统的学术影响）维度的计量指标进行分级分类，具体分为两级。一级指标共5个大类，分别是论文使用（C1）、专著获取（C2）、网络分享（C3）、网络提及（C4）、社会应用（C5）。二级指标共18个小类，论文使用包括知网论文下载数；专著获取包括图书销售、图书馆藏书，其中，图书销售又包括京东、当当、孔夫子销售和读者评分；网络分享包括百度文库、豆丁网、doc88、book118、博客；网络提及包括搜索引擎采集到的精确匹配提及网页；社会应用包括新闻、百科、评论、综述，其中百科只包括知识百科，不包括人物百科。

4.2 极端异常值的常规识别与抗差性识别方法对比

首先，对5个一级指标按Ⅰ（表1）即零值完整保留，得到无任何缩减的数据集，简称无缩减集。依据四分位距（上四分位值与下四分位值之差即IQR=Q3-Q1）绝对值大于3倍四分位值的区间设定为极端异常值（extreme qutlier），即极端异常值依据

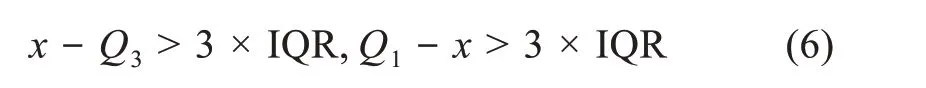
进行常规识别（或抗差性识别）。依据异常值识别的常规方法，数据集零值无缩减即全保留，得到常规识别异常点检定结果，如表1（Ⅰ）所示。

其次，对2个零膨胀分布一级指标C2、C5，按照前述抗差性控制要求，对数据集Zr按公式(2)进行四分位自适应零调整，得到零值有限缩减的数据集，简称零值缩减集。代入公式(6)，依据异常值识别的抗差性方法，得抗差性识别异常点检定结果，如表1（Ⅱ）所示。

同时，保留非零膨胀分布一级指标C1、C3、C4的常规识别异常点检定结果，得到汇总数据（表1）。

表1 极端异常值的常规识别与抗差性识别结果

从表1可见，常规识别异常点有115个，抗差性识别异常点有44个，其中指标C2、C5的异常点识别结果差异最大，为此，采用箱线图进行直观对比。

从图1的C2无缩减集可见，由于受高零值和零膨胀的影响，C2的常规识别中，异常点的图框中线和顶部都已接近零，极端异常点达到68个，而C2的非零值数据总共才93个，可见常规异常值识别不具有抗差性。相反，从图1的C2零值缩减集可见，在采用公式(2)进行四分位自适应零调整、缩减111个结构性零后，C2的抗差性识别中，异常点的图框顶部已得到明显提升，指标C2的极端异常点降到11个，异常值识别和检定的抗差性大大提高。类似情况在指标C5中也有充分体现。由此可见，四分位零值缩减法处理对于零膨胀下极端异常值的识别，具有很强的适切性和抗差性，是异常值合理修正及其稳健计量的重要基础。

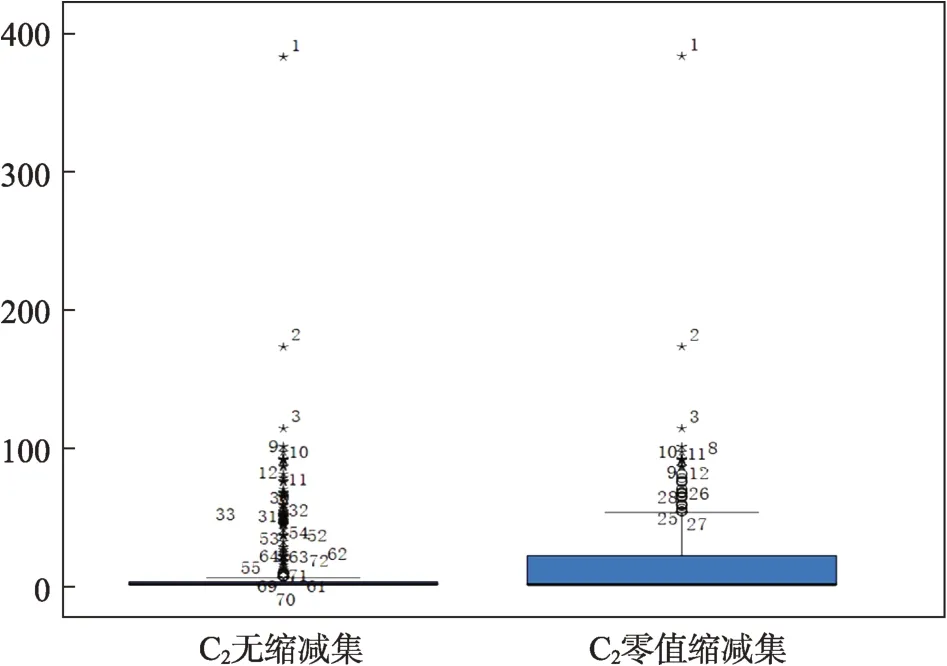
图1 C2无缩减集与零值缩减集的箱线图对比

4.3 极端异常值的缩尾求稳修正方法

对于检定后的表1极端异常值，可采用缩尾求稳和缩序求稳两种方法修正。缩尾求稳修正应用缩尾值公式(4)和公式(5)，将极端异常值替换为最接近极端异常值的值即中度异常值的最大值，模拟条件下则将异常值替换为边界值X([αn])和X([(1-α)n])最接近的模拟值，方法相对成熟和简单。缩序求稳修正将另文研究。

按照以上缩尾求稳方法和缩尾值计量结果，重新计算5个一级指标数据集的主要统计量和统计参数，得到表2。

从表2可见，极端异常值较多的C3、C2、C1最大值显著降低，缩尾求稳修正后的数据集（修正值即缩尾值）降低了原始观测值的数量级，在一定程度上实现了异常值的降维、降权和一致性，为下一步的无量纲化和多指标综合评价结果提供了良好基础。显然，修正后的数据集在最大值、均值、标准差和方差等方面，都比修正前的数据集更具耐抗性和可靠性，数据集的极端右偏斜分布偏差和误差得到有效抵抗和削弱。

表2 缩尾求稳修正前后的主要统计量和参数

5 稳健计量在国家社科基金评价中的应用

网络-替代计量数据的异常值识别和修正，极大地提高了原始数据集的合理性和稳定性，但在综合评价的稳健性上仍然面临两大问题：一是指标数据的量纲和量级不同，如何进行稳健性的无量纲化和计量；二是各项指标的重要性和数据信息不同，如何进行稳健性的权重系数求解和综合评价。

5.1 稳健性无量纲化的方法选取及其应用

指标数据的无量纲化处理有线性无量纲化和非线性无量纲化两种，前者能保留原始数据集的分布形态，后者则会改变原始数据集的分布形态。本研究对44个极端异常值的识别和合理修正，可以看作一种极大型区间的线性预处理，是稳健计量评价的重要基础。线性无量纲化具有保留原始数据分布特征和简单实用的优点，且极端异常值对线性无量纲化的干扰已经排除，因此本研究不再考虑非线性无量纲化。

线性无量纲化处理的方法主要有标准化法、归一化法、极值法、线性比例法、功效系数法和向量规范法等；其中线性比例法的比例系数可取最大值、最小值、均值等，分别称为最大值法、最小值法、均值化法。这些方法之所以不同，是因为采用不同的特殊值和线性函数进行一致性映射与转换，因此产生不同的评价值和综合评价结果。

在标准化法、Z-Score法和特殊值取均值、总和、平方和的线性比例法中，由于特殊值和线性函数中包含样本整体信息的统计量，一致性和稳定性都较好。其中，标准化法、Z-Score法会使组内方差和变异系数发生巨大改变，说明组内信息受损严重，一致性差；极值法、最大值法、最小值法和功效系数法，由于特殊值和线性函数中值只包含样本信息的个别特殊统计量（如最大值、最小值等），容易受到极端数据分布的影响，且不能明显缩小各指标间数量级差异，稳定性和一致性都较差。

在常用的无量纲化方法中，作为线性比例方法的均值化法，由于受极端值的影响相对较小，能缩小各指标间数量级差异并显现原始数据集的差异信息，且变异系数不变，主要统计量和参数的稳定性、一致性都较好。此外，均值化法在基于序关系分析法（G1法）的综合评价应用中，还能使指标权重对评价值的影响实现一致性和稳定性。因此，从无量纲化方法选取和一致性转换的诸多因素综合考虑，基于均值的线性比例法都是一种比较理想的稳健性无量纲化方法。

由于均值化法易受样本值，特别是极端值的影响[37]，基于稳健性要求，可采用基于缩尾求稳或缩序求稳的方法对原始数据集的异常值进行修正，本研究采用前者。

修正后的数据集，因采用缩尾值代替原始值中的极端异常值，消除了异常值对样本值的影响，使均值化转换的特殊值（缩尾均值）更能显现差异信息。均值化法计算公式为

其均值化法处理后的主要统计量和参数如表3所示。

从表3及与表2的对照可以看出，采用基于缩尾均值的线性比例方法处理后，各指标间缩尾值（修正值）的数量（级）差异，与原始值相比得到有效缩小，因此数据集的极端右偏斜分布得到改善，极端异常值较多的C3、C2、C1最大值显著降低；指标重要性高的C5，方差分量提高幅度最大，最大值为5个指标中最高；最大值和方差都在较小差异的同一值域范围内，且基本反映了各指标间的重要性，原始数据集的信息差异得到显现。基于缩尾均值的线性比例方法转换，因信息变异受损较低而更加稳定和一致。

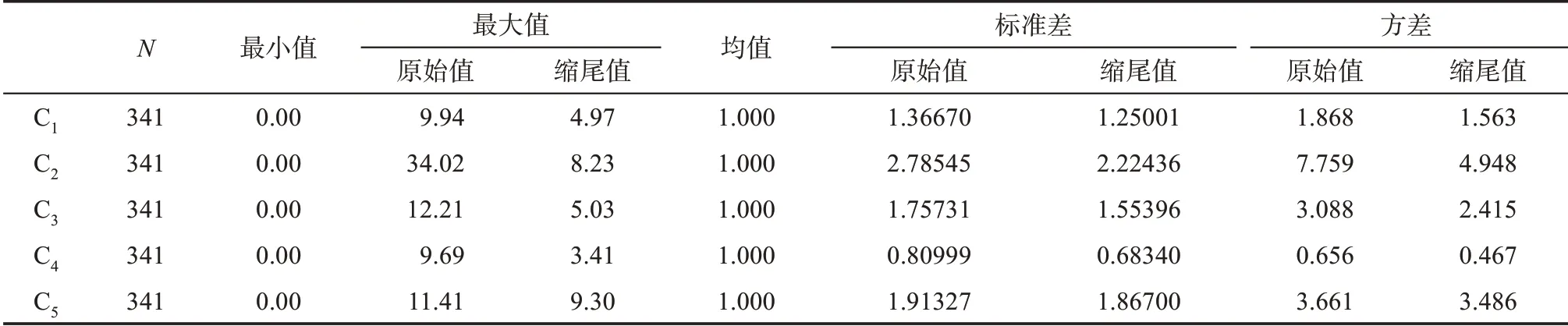
表3 均值化法处理后的主要统计量和参数（基于原始值和缩尾值）

5.2 稳健性权重求解及方法选取

指标属性的重要性和主观权重求解，如何反映客观的计量信息，使权重求解及其实现机制更具可靠性和可信度，是稳健计量评价需要考虑的另一个重要问题。

多指标综合评价是一种基于原始值（修正值）计量、特殊值转换和评价值综合或聚合的价值测度体系，其价值测度的实现主要有四种途径：一是基于计量对象的客观赋权法，代表方法有熵权法、DEA（data envelopment analysis）法、标准差法、变异系数法，能反映数据样本的相关性和信息量，但缺乏评价方法和结果的一致性和稳定性，方法不同导致结果也不同；二是基于评价主体判断的主观赋权法，代表方法有AHP（analytic hierarchy process）法、Delphi法、G1法，能反映指标本身的重要性程度和专家群体的知识，但缺乏评价前提和过程的可靠性和可信度，权重赋值与计量数据无关；三是基于对象和主体的主客观赋权法，也称为组合赋权法，代表方法有平均值法、Borda法、Copeland法、最小二乘法、离差最大化法，能综合反映主客观判断，但缺乏方法和评价体系的一致性，体系和评价方法存在冲突或“硬性”；四是基于多种数学模型的合成优化法，代表方法有非线性优化法、线性优化法，能不区分主客观差异融合多种评价方法，但缺乏评价方法和结果的适切性，评价目标或准则依赖主观判断[38]。

尽管不同的权重求解方法有不同的实现机制，但基于一种主观权重求解同时又完全融入一种客观权重求解，可以构造出一种同时具有主观可靠性和客观可信度的新方法。本研究选取的G1法应用，有机融入客观赋权法（标准差法），使其兼具两种方法的优点，克服各自的不完备和非稳定性局限。

5.3 稳健G1法及其权重系数求解应用

稳健G1法是一种在主观赋权法中融入客观赋权法，将专家群体的理性判断和样本数据的客观信息量有机结合的权重求解方法。权重主观可靠性和客观可信度的优势互补，使权重值具有主观-客观双实现机制，从而提高综合评价结果的可靠性和稳定性。

G1法也称为序关系分析法，是一种传统的主观权重求解方法[39]。权重系数求解基于国家社科基金成果社会影响指标的序关系分析，有10位咨询专家参与，通过调查问卷评分方式，得到5个指标的重要性程度及其rk赋值信息。专家根据自己的经验和偏好，对5个指标的重要性程度，按从强到弱顺序确立序关系，并对5个指标的重要性标度ωk-1/ωk进行理性判断。

若在m个评价指标中，专家给出两个指标之间的重要性程度之比为rk，则权重系数的求解公式为

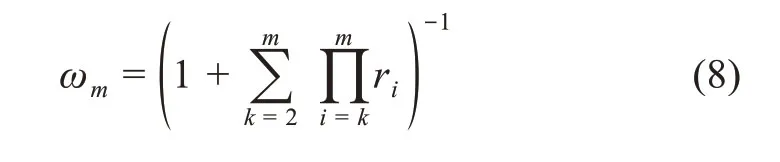
专家建立的序关系和相对重要程度rk赋值以及G1法权重系数求解结果如表4所示。

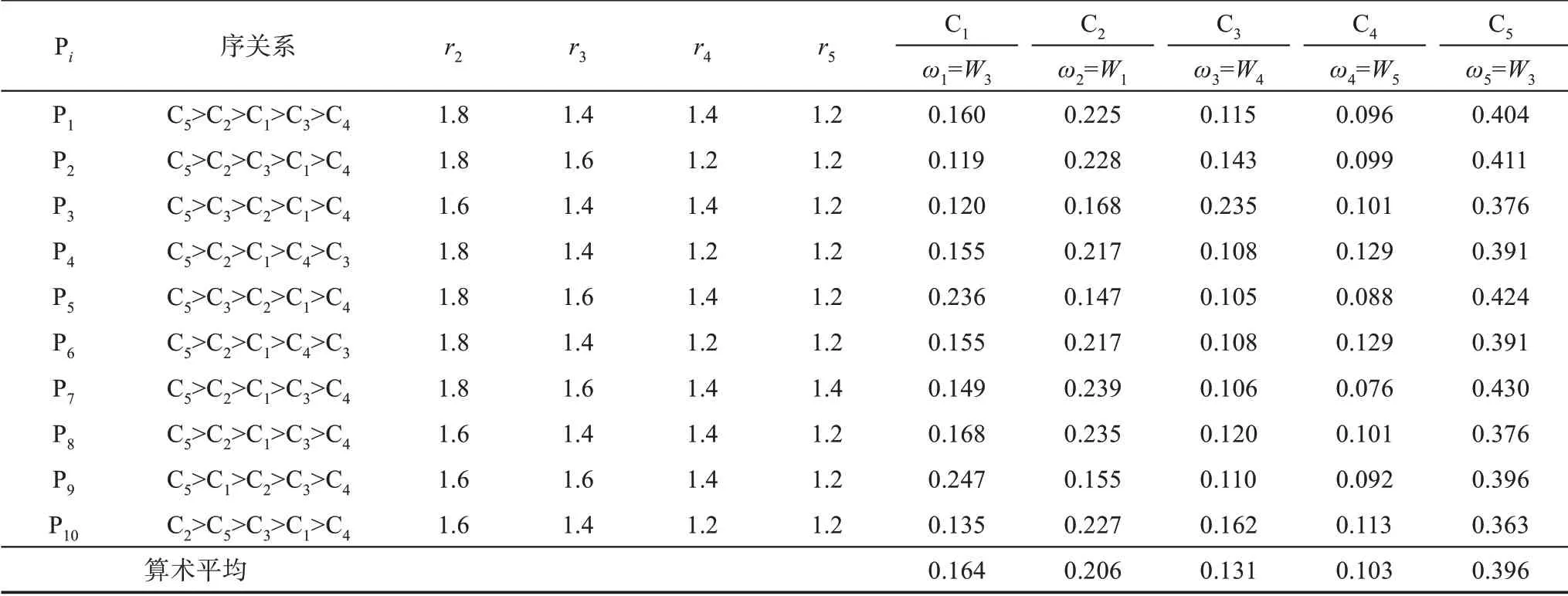
表4 G1法序关系、rk赋值及其权重系数求解结果

从表4可见，不同的专家有不同的序关系判断及其rk赋值和权重系数。通过G1法10位专家群体权重系数的算数平均，得到指标C1、C2、C3、C4、C5的群体权重系数，分别为0.164、0.206、0.131、0.102、0.396，即群体确立的最终序关系为C5＞C2＞C1＞C3＞C4。

在传统的主观赋权法中，G1法采用专家群体的知识判断，评价方法和结果具有很强的一致性和稳定性；但由于不能反映数据样本的相关性和信息量，评价前提和过程缺乏客观可靠性和可信度。依据李刚等[40-41]提出的标准差修正G1组合赋权及其合理性研究，以及易平涛等[42]提出的一种取代传统主观序关系的客观序关系分析法，本研究构造出基于标准差的客观G1法和半客观G1法，并与G1法有机融合，最终形成稳健G1法。

客观G1法的序关系建立，不是直接采用专家群的知识判断，而是根据样本数据中的信息量即相邻指标标准差的大小（见表3），重新确定序关系及相对重要性程度rk赋值，并通过公式(8)求解权重系数。根据表3，原始值的标准差序关系为C2＞C5＞C3＞C1＞C4，rk赋值分别为1.69、1.46、1.28、1.09。将rk赋值代入公式(8)，得到基于原始值的客观G1法C1、C2、C3、C4、C5的权重系数值，分别为0.121、0.384、0.156、0.112、0.227。同理，根据表3，可得到基于缩尾值（修正值）标准差序关系及rk赋值，分别为1.83、1.24、1.20、1.19，代入公式(8)得到相应指标权重系数值，分别为0.138、0.376、0.165、0.116、0.205。

半客观G1法是利用G1法专家群体确立的序关系，计算C5＞C2＞C1＞C3＞C4相邻指标的σk-1/σk之比作为rk赋值，再根据表3原始值（或缩尾值）的标准差序关系，代入公式(8)。同时，对rk进行如下限定：

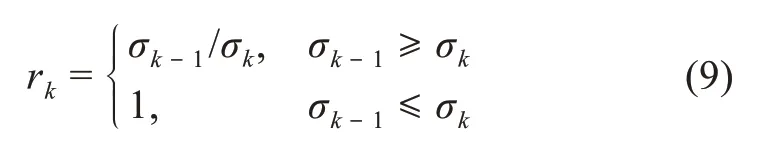
得到基于原始值标准差序关系修正后的rk赋值，分别为2.17、2.04、1.00、1.00，通过公式(9)并参照表4，重新计算基于原始值的半客观G1法C1、C2、C3、C4、C5的权重系数值，分别为0.106、0.215、0.106、0.106、0.467。同理，根据表3的缩尾值，通过公式(9)并参照表4，可得到基于缩尾值标准差序关系修正后的rk赋值，分别为2.27、1.78、1.00、1.00，相应指标权重系数值分别为0.113、0.202、0.113、0.113、0.459。

将以上权重系数求解结果汇总，得到表5。

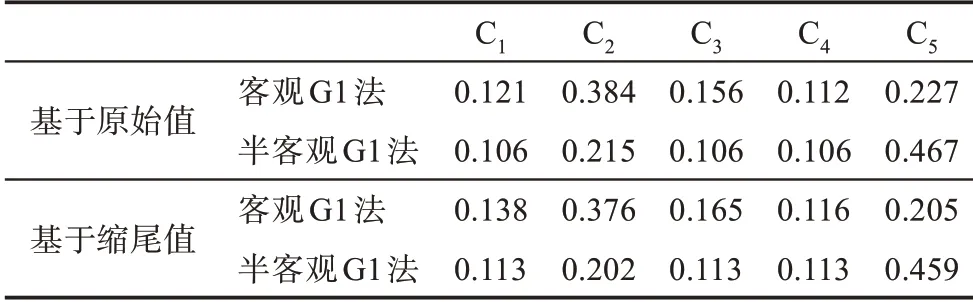
表5 客观G1法、半客观G1法权重系数求解结果

基于权重系数求解的主观-客观双实现机制要求，将表4中的G1法权重集和表5中的客观G1法、半客观G1法权重集，看成一个三角模糊数，进行去模糊化处理，转化为精确值，得到稳健G1法的最终权重系数修正值。具体计算依据梯形重心法公式

将表4和表5的3种G1法的权重系数代入公式(10)，得到基于原始值的稳健G1法C1、C2、C3、C4、C5的权重系数修正值，分别为0.147、0.237、0.131、0.105、0.380；基于缩尾值的稳健G1法C1、C2、C3、C4、C5的权重系数修正值分别为0.151、0.233、0.134、0.107、0.375。以上最终权重值的序关系与G1法一致，因此，稳健G1法实现了具有客观可信度的样本信息量，与具有主观可靠性的专家群知识的有机融合。

5.4 稳健性方法在国家社科基金成果评价中的具体应用及结果

在国家社科基金成果的社会影响评价应用中，稳健性计量评价有以下重要步骤。

（1）极端异常值的检定和计量处理。基于抗差性控制要求进行异常值识别，将原始值（数据集）的极端异常值修正为稳健性的缩尾值。

（2）无量纲化处理。对于修正后的数据集，应用基于缩尾均值的线性比例方法，得到更具稳定性的无量纲化值；为了对比，同时也对修正前基于均值的指标值进行无量纲化处理。

（3）指标权重系数的稳健G1法求解。基于专家群体知识，以及客观和半客观序关系（标准差）信息，得到具有主观-客观双实现机制的权重系数。稳健G1法的标准差来自修正后的数据集，非稳健G1法的标准差来自原始数据集。

（4）基于以上处理和求解计算综合评价值，得到具有稳健性或非稳健性的综合评价结果。

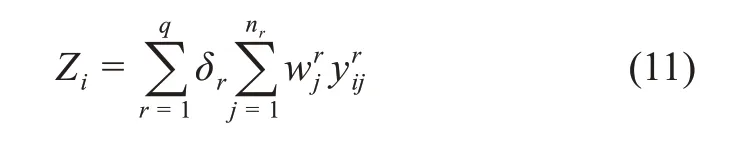
对于国家社科基金项目成果的社会影响评价来说，综合评价值越大，则社会影响越大。

为了与稳健方法进行对比分析，本研究同时也基于原始值（完全保留极端异常值）进行非稳健的无量纲化、权重系数求解和综合评价，其方法、步骤与基于缩尾值（修正值）的稳健方法一致。基于缩尾值的稳健综合评价和基于原始值的非稳健综合评价结果及其排序对比如表6所示。

从表6可见，基于缩尾值的综合评价排序和基于原始值的综合评价排序差距较大，在前10%排序中，最大秩距33位；其中，成果《主体功能区人口再分布实现机理与政策研究》如果基于缩尾值，排序第34位，但如果基于原始值，即完全保留极端异常值，则排序第1位。也就是说，在本研究341个对象的排序中，社会影响排名第1位的科研成果因为一个极端异常值，最终结果可以从第34位跃升至第1位；但如果基于缩尾值即稳健的综合评价排序，这项成果就只能从第1位跌落至第34位。由此可见，基于稳健方法的计量和评价，对于综合评价的真实性和合理性具有极其重要的影响和作用。此外，从有异常值的指标个数看，在社会影响排名前10%的科研成果中，有13项成果有极端异常值，占比达到38%；其中，有2个及以上极端异常值的成果2个。非稳健计量评价对综合评价的真实性和合理性可能产生重大的偏差和影响，因此，基于稳健方法的计量评价具有重要的理论意义和应用价值。

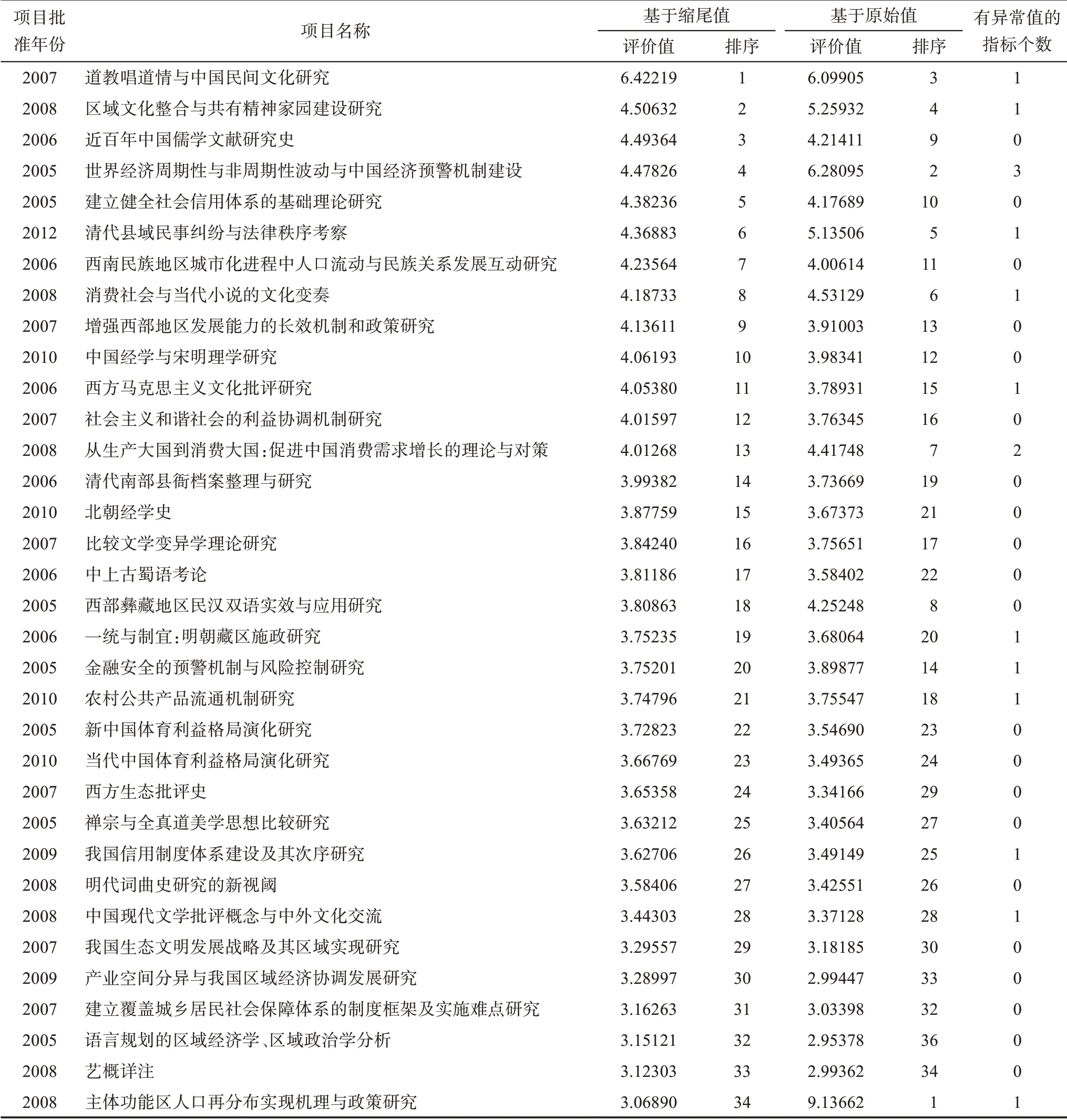
表6 稳健和非稳健综合评价计算结果及其排序

此外，表6还对34项成果的批准年份进行了统计，可初步观察指标值和时间因素之间的相互影响。在社会影响最大的34项成果（前10%）中，有30项 是 前5年（2005—2009年）的 成 果，占 比88.24%，只有4项是后5年（2010—2014年）的成果，占比11.76%，说明成果时间越早影响越大；尽管有些指标数据在早年的网络平台上量值不高或没有，但因排序前34项成果的单指标数据覆盖率都达到100%（无零值），这部分成果受影响不大。因此，应重点关注计量评价的时间累积效应，建立一种更精确的基于时序动态响应的稳健计量评价方法。

6 结论及建议

传统计量评价对网络环境下科学成果的社会影响及其数据集的不确定和不完备局限或缺陷并不十分清楚。本研究基于网络-替代计量下高零值、多异常值和极端右偏斜分布的复杂挑战及其机理分析，通过四分位零值缩减法、异常值缩尾求稳法，以及权重系数稳健G1法等方法创新，探讨数据集的真实性、合理性及其计量评价的抗差性、可靠性和稳定性与社会影响评价之间的复杂联系和科学出路，得出以下结论及建议。

（1）对于左侧高零值和零膨胀分布挑战，零值的全截断不但会使样本结构严重丢失，而且会导致右侧异常点的检测结果大大降低；但如果零值全保留，又会因零膨胀导致右侧异常点大大增加，Zr≥75%异常值甚至无法检测。由于数据集存在多异常值，计数模型中基于零膨胀的总体混合概率必然受到影响，其真实的或过度的零值拟合数据也不可靠。相反，计量模型中基于Qr控制函数的缩减法，则可以完全避开计数模型中的多异常值影响，能比较好地解决零膨胀及其异常值检定的抗差性问题，在既不全截断也不全保留中找到一个危险率较低的理想点。

因为四分位异常值识别的基本假设是基于四分位距的稳健性，将Q4和Q1截断，且Q3-Q1＞0，以中间分位的尺度参数作为样本的总体估计。Zr≥75%时，Q3=Q1=0，Zr的缩减率必须大于0.25，即Zr-Qr＞0.25，这既是异常值检定的充要条件，也是异常值检定的“必要变异度”。因此，在零调整的缩减率渐进于0.375时，由于Zr≥75%，Qr缩减的值域危险率应该扣除0.25的“必要变异度”；扣减后的缩减率才是实际危险率，它的最大值为0.125。而0.125正好是一个分位的中位数，对于三个分位的支撑集而言，属于危险率较低的理想位置参数估计点。这就说明，即使Qr缩减的最大值域为临界值0.375，它的实际危险率仍处于0.125的较低水平。

由于四分位零值率是从具有稳健性的四分位距法进行定义和推导的，且符合高零值样本置信区间理论和零膨胀样本结构理论及其方法，以及Brookes提出的“解释信息计量分布的长尾必需用等级”的方法[27]，Cronin提出的替代计量学的“必要变异度定律”（law of requisite variety）[43]，因而对于高零值条件下的异常值自动检测和识别，四分位零值缩减法具有很强的适切性。经过一致性逼近校正后，四分位零值率及其精确计算公式还具有很好的一致性和抗差性，是异常值合理修正及其稳健计量的重要基础。未来在信息计量学、评价学和统计学及其相关学科中，这种四分位自适应零调整方法可以得到更广泛的应用。

（2）对于数据集右侧的多异常值和极端右偏斜分布挑战，釆用基于缩尾均值的缩尾求稳方法处理，不但能消除极端异常值的影响，而且还能使数据的样本大小保持不变，防止总体信息丢失，使右侧数据在一定程度上实现降维和降权。

权重系数求解基于主观赋权法，有机融入客观赋权法，构造出一种具有客观可信度的样本信息量，与具有主观可靠性的专家群知识有机融合的评价方法。通过梯形重心法公式，将G1法（主观）和客观G1法、半客观G1法的权重集看成一个三角模糊数，进行去模糊化精确处理，得到稳健G1法的最终权重系数修正值，使权重值具有主观-客观双实现机制，从而提高了综合评价结果的可靠性和稳定性。

（3）应用研究表明，基于缩尾值的综合评价排序和基于原始值的综合评价排序差距较大。因此，科学成果的非稳健方法，对于综合评价的真实性和合理性可能产生重大的偏差和影响，科学成果的稳健计量评价具有重要的理论意义和应用价值。

与非稳健计量评价方法的对比，稳健计量评价通过高零值下四分位零值率的抗差性检定、多异常值下的缩尾求稳、极端右偏斜分布下基于缩尾均值的线性比例映射及其权重系数主客-客观双实现求解等方法的应用，使计量评价的稳定性、可靠性和抗差性都大大提高。

尽管科学成果及其社会影响的计量评价面临数据集左侧、右侧和极端向右偏斜分布之间的复杂关系及其由此带来的诸多科学挑战，特别是方法和结果的抗差性、可靠性和稳定性，但同时也带来诸多科学机遇，有利于促进信息计量学、评价学及相关学科向复杂性精确科学方向发展。现在，即使是存在高零值和多异常值数据，即若有蓄意通过网络-替代计量数据（如点击率）来提升成果的社会影响，稳健性计量评价也有相当可靠和稳定的方法进行有效抵抗、削弱或消除。未来的发展方向，建议研究一种比基于必要变异度定律更复杂和精确的基于稳健变异度定律的缩序计量方法，以及一种基于时间累积的时序动态响应计量方法，以对数据普遍存在的计数为0及其他不规则性进行积极防御和高效抵抗。