端面超精密车削中的面型误差辨识技术研究

马善意，杨辉，赵宏鑫，张彬，滕凯冰

(北京航空精密机械研究所精密制造技术航空科技重点实验室，北京 100076)

0 前言

随着光电技术的快速发展，对于亚微米级面型精度和纳米级表面粗糙度的超精密光学元件需求日益增多[1]，单点金刚石车削加工技术以其效率高、精度高的优势，在先进光学制造领域中得到了越来越广泛的应用[2]。然而，在实际加工过程中，无论是加工环境还是加工系统都不是处于理想的状态，其中存在的干扰因素会对所加工光学表面的面型精度产生影响，最终会降低整个光学系统的质量[3]。对于系统误差的影响，通常采用补偿的方式来提高面型精度[4]，而误差补偿的前提是对误差的来源进行辨识。因此，对误差的准确辨识可以为后续干扰因素的排查和误差的补偿提供参考。对于面型误差的辨识和补偿，已有科研人员展开了大量的研究。RAHMAN等[5]分析了多轴机床的误差来源，并建立了机床误差的数学模型。LI等[6]基于多体系统动力学理论建立了五轴机床的误差模型，完整描述了机床误差与刀具位置误差的传递关系。KONO等[1]通过对加工误差作快速傅里叶变换，将不同来源的误差进行区分，并进行相应的补偿，使面型精度提升了62%。LIU等[7]通过仿真模拟了不同误差来源对面型精度的影响，并对一个平面-球面工件的主要加工误差进行了辨识。LEE等[8]研究了对刀误差的影响，并总结出了凹形非球面超精密车削中由对刀误差引起的面型误差特性。MIR等[9]建立了一个数学模型，该模型可用于预测几何误差所引起的刀尖位置误差，并依据模型来对机床的各运动轴进行补偿。ZHANG、DAI等[10-11]研究了对刀误差对切削力的影响，并建立了切削力与对刀误差之间的数学模型，实现了对刀误差的在线识别。HUANG等[12]建立了空气静压轴承主轴的动力学模型，对主轴动平衡的影响进行了分析，并通过实验验证了该模型的准确性。ZHANG等[13]研究了主轴动不平衡时的主轴动态特性及其对加工表面的影响。YUAN和NI[14]开发了一种运动误差补偿系统，该系统可以对机床的几何误差进行离线辨识和补偿，然后利用误差模型估计和补偿切削力误差和热误差。SZE-WEI等[15]开发了一种超精密车床的误差补偿系统，该系统通过测量工作台运动的直线度误差，并将其反馈给精密刀具伺服系统，可对误差进行实时补偿。综上，大多数的研究工作主要集中于误差模型的建立、模拟以及误差的补偿。本文作者为实现误差模型理论的实验验证，并进一步提高国产超精密机床的加工精度，基于国产超精密机床Nanosys600对样件Al6061进行单点金刚石车削实验，对已加工表面轮廓进行测量、滤波；根据各误差来源所引起的面型误差特征，辨识出存在的误差来源，并排查误差项。

1 加工过程中对面型精度的干扰因素

1.1 环境温度

环境温度对面型精度有着极大的影响，机床在加工过程中会受到外部热源的影响产生热量在机床各部位之间传递，由于每个零件的形状、结构、材质及约束条件不尽相同，导致在热量的传递过程中会引起零件之间的拉、压、弯、扭等作用，最终使机床零件产生形变。而这些形变叠加在一起反映到刀具和工件的相对运动关系中，致使刀具的实际运动轨迹偏离理论轨迹，从而导致面型精度下降[16]。温度引起的面型误差一般在空间频域中处于较低的频率值，在时间频域中的频率值只与外界温度的变化频率相关，而与选定的工艺参数无关。

1.2 几何误差

1.2.1 机床结构分析

所使用的设备为国产超精密车削机床Nanosys600，如图1所示。Nanosys600采用T导轨布局，x轴和z轴垂直布置，主轴安装在x轴上，工件吸附于主轴末端的真空吸盘，刀架安装在z轴上，金刚石刀具固定于刀架前端，如图2所示。机床的拓扑结构如图3所示。可知：机床的运动传递链分成两个分支，一个为刀具分支，主要由床身、z轴、刀具组成；另一个为工件分支，主要由床身、x轴、主轴、工件组成。在加工过程中，刀具的切削点与工件材料的被切削点重合，使得该拓扑结构闭环。

图1 Nanosys600超精密机床

图2 Nanosys600结构示意

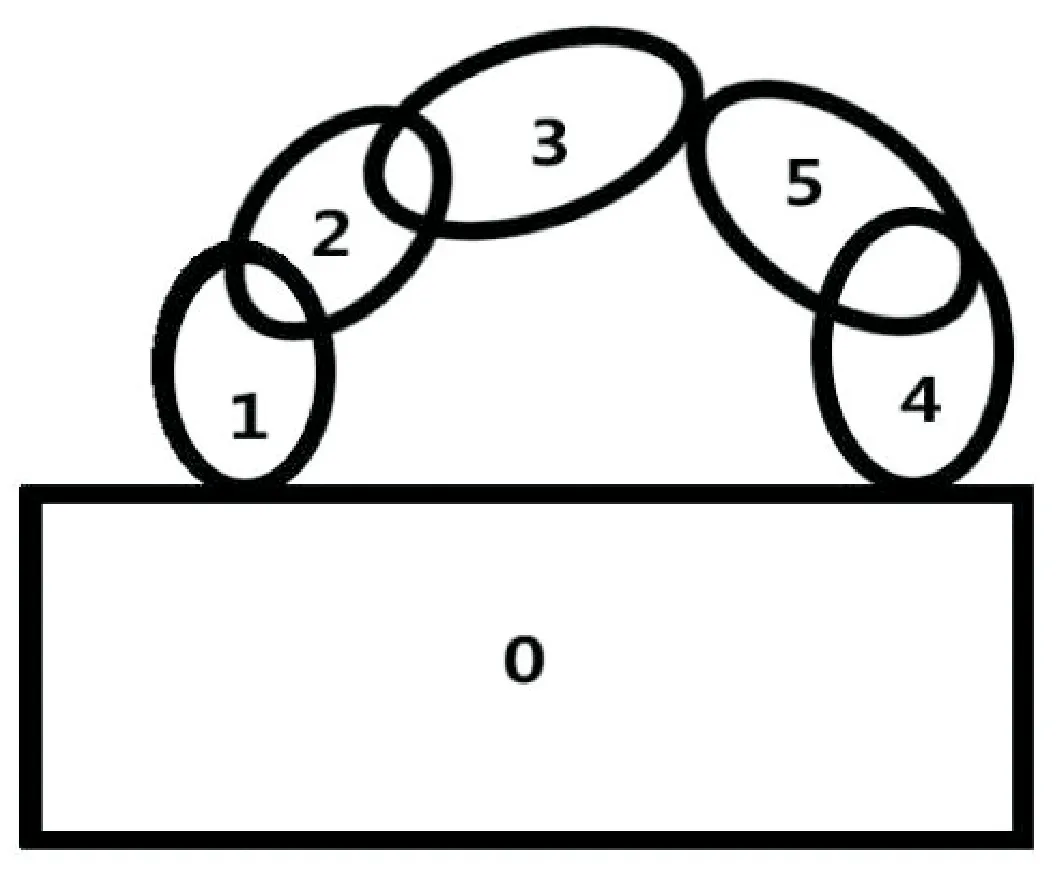
图3 Nanosys600拓扑结构

低序体阵列法是描述拓扑结构的一种常用方法，该方法简洁方便，且适用于计算机自动描述多体系统。其基本思想为按自然增长数列，从一个分支到另一个分支依次为各部件编号[17]。低序体阵列可由如下公式表示：

Ln(j)=i

(1)

其中：i为j的n阶低序体。对于相邻体i和j而言，有

L(j)=i

(2)

根据低序体理论，结合图3，列出Nanosys600超精密机床的低序体阵列表，具体如表1所示。

表1 Nanosys600超精密机床的低序体阵列

考虑到机床实际的约束情况，对相邻体的自由度情况进行描述，如表2所示。其中：x、y、z分别表示3个坐标轴方向的自由度；α、β、γ分别表示绕x、y、z轴旋转的自由度。

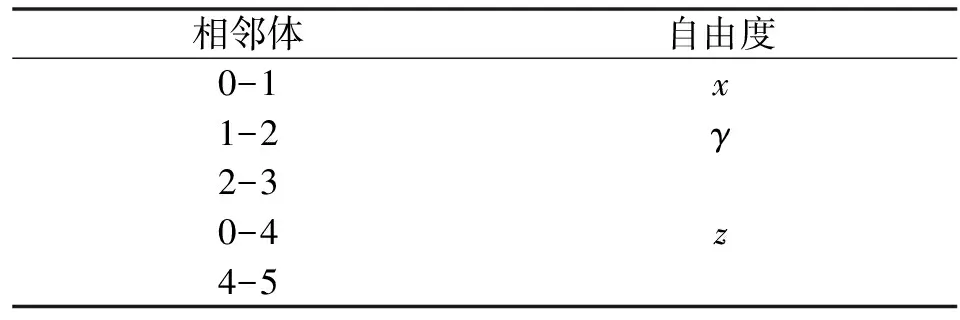
表2 相邻体自由度

1.2.2 几何误差的来源

超精密车床的直线运动由直线电机驱动完成，理想情况下，工作台沿固定方向移动，只有一个自由度。然而在实际情况中，由于制造装配过程中产生的误差以及实际切削过程的影响，导致直线运动具有6个自由度的运动误差，这6项误差可分为3项平动误差和3项转角误差。以δpq代表平动误差，θpq代表转角误差，下标p和q表示该误差是沿着机床p轴(p∈{x、z、C})运动在q方向上(q∈{x、y、z})产生的。对x轴而言，其6项误差可以表示为δxx、δxy、δxz、θxx、θxy、θxz,其中，δxx为x轴的定位误差，δxy、δxz为x轴沿2个方向的直线度误差。

超精密车床的工作主轴一般都使用空气静压主轴，该类型主轴具有回转精度高、调速方便、寿命长、运行稳定、干净、无污染等优点。理想情况下主轴绕其轴线方向旋转，只拥有一个自由度。但在实际情况中，由于回转轴线的位置偏差，旋转轴在运动过程中也有6个自由度的运动误差。

此外，轴与轴之间还存在垂直度误差，因此，Nanosys600共存在21项几何误差，如表3所示。

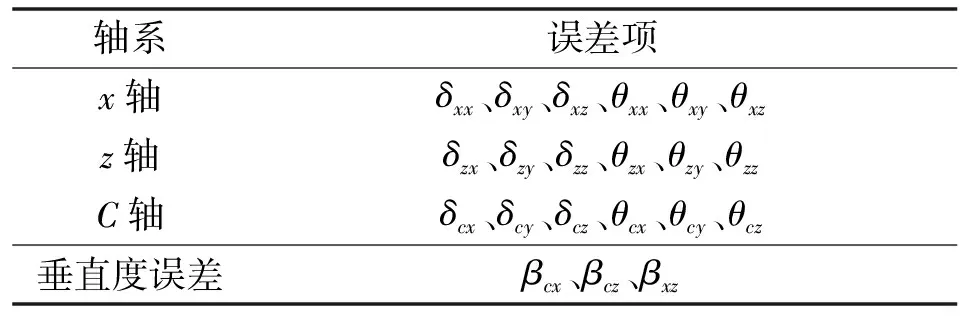
表3 Nanosys600几何误差

2 端面车削实验与误差来源辨识

采用的刀具为上海某公司的单晶金刚石车刀，刀具前角0°，刀尖圆弧半径2.0 mm。采用工艺参数为主轴转速500 r/min、进给速度1 mm/min、背吃刀量10 μm，对Al6061进行单点金刚石车削。在Taylor Hobson PGI Optics轮廓仪下得到的面型结果如图4所示。由于此实验的目的在于对面型误差进行分析，可使用低通滤波将高频的噪声过滤掉，避免粗糙度和毛刺带来的干扰，滤波后的结果如图5所示。可以看出：面型轮廓中存在着低频振荡，初步判定该面型误差由温度的波动导致。在其他参数不改变的前提下，将进给速度调整为2、4 mm/min，得到的面型轮廓结果分别如图6、图7所示。可以看出：该误差的空间频率在进给速度增大时呈等比例增加，在时域中保持着周期约20 min的波动，且波峰波谷值出现的位置没有明确的规律，这与温度影响的特点相符。

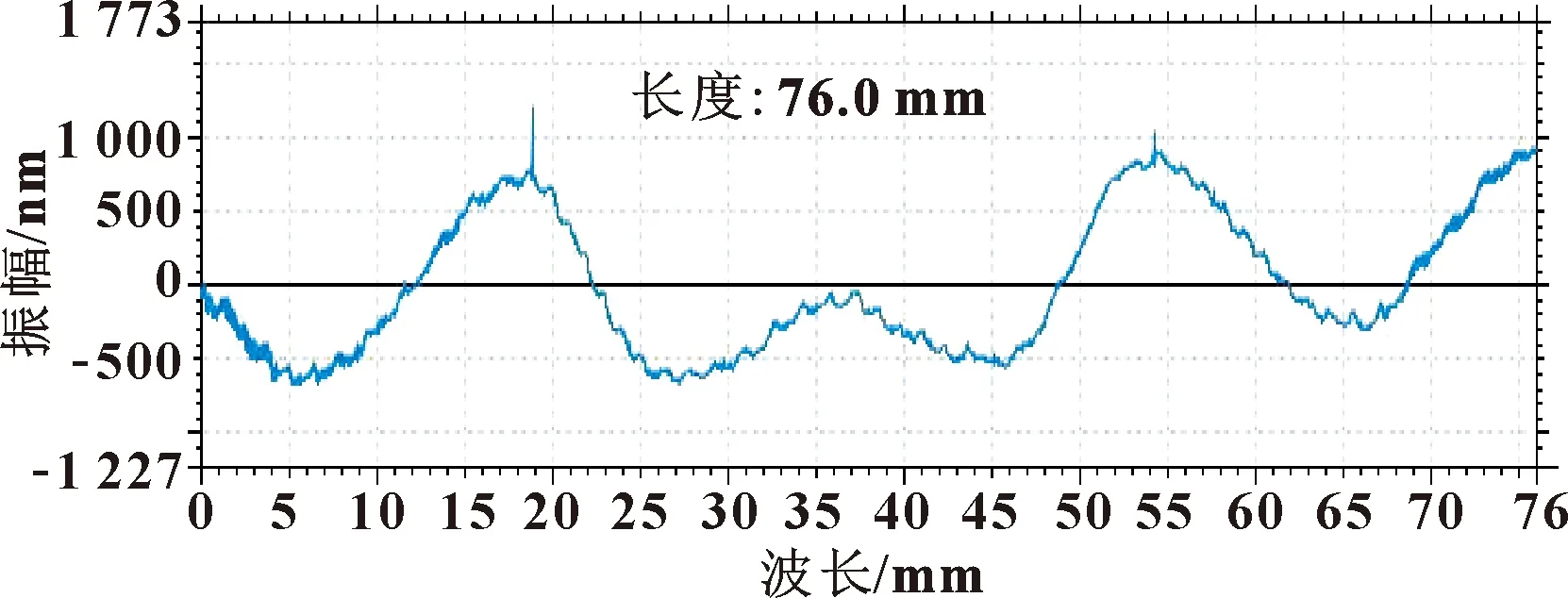
图4 进给速度为1 mm/min时的加工滤波前面型轮廓

图5 进给速度为1 mm/min时的加工滤波后面型轮廓

图6 进给速度为2 mm/min时的加工滤波后面型轮廓

图7 进给速度为4 mm/min时的加工滤波后面型轮廓

对实验室的温控系统进行检修后再次以工艺参数为主轴转速500 r/min、进给速度1 mm/min、背吃刀量10 μm对Al6061进行单点金刚石车削，得到的面型轮廓结果如图8所示。可看出：轮廓曲线中心下凹。为确定该误差为系统误差，以同样的参数再重复进行2次实验，得到的结果分别如图9、图10所示。可知：轮廓曲线相似，且Pt值(波峰波谷差值)相差不大。由此可确定该误差为系统误差，初步认为是由于x轴导轨直线度误差引起的。由于平面切削的敏感方向为z方向，所以引起该面型误差的误差项应为δxz。

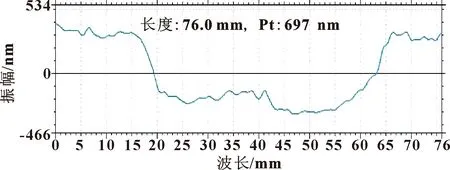
图8 温控系统检修后第1次加工

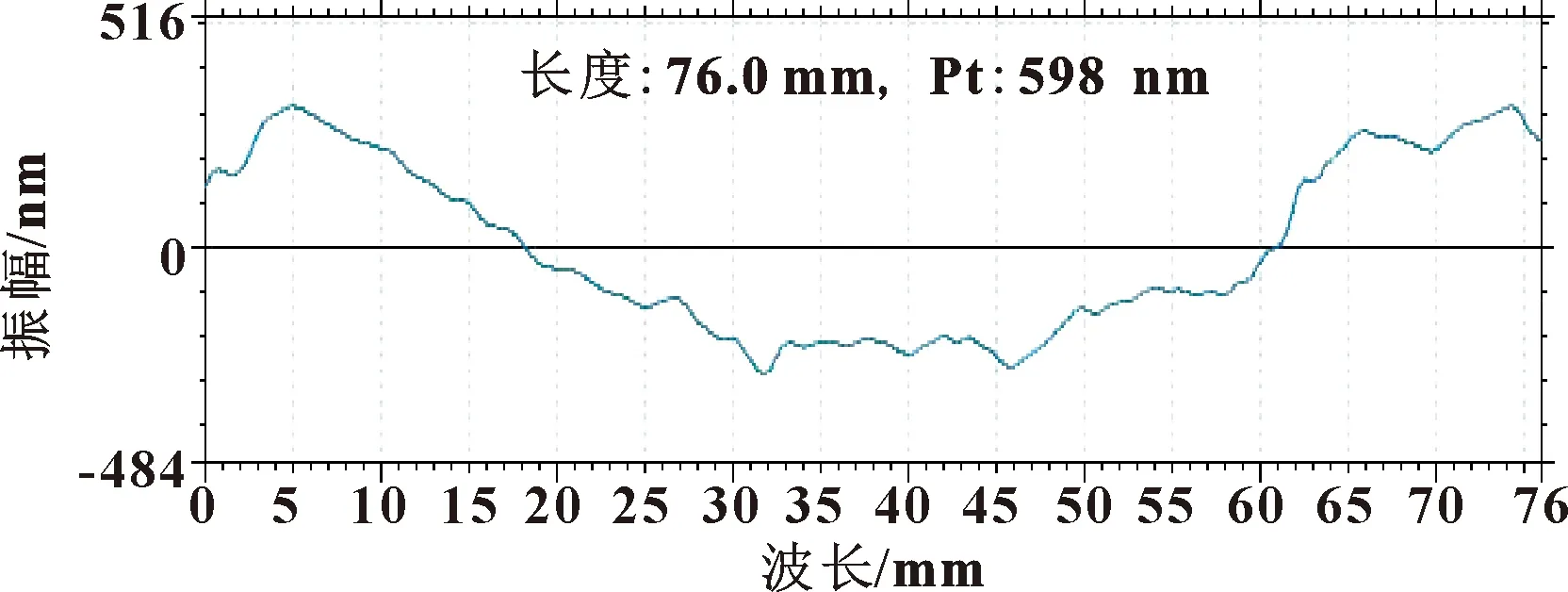
图9 温控系统检修后第2次加工

图10 温控系统检修后第3次加工

为验证以上推测，更换刀架的位置，以改变x轴导轨的工作位置，采用以上参数进行加工，得到的轮廓面型如图11所示。可以看出：Pt值较小，仅有203 nm，且不存在系统误差。

图11 更换导轨工作位置后的面型轮廓曲线

3 结论

本文作者分析了超精密切削过程中典型干扰因素对面型精度的影响机制以及这些干扰因素所引起的面型误差特性。采用国产超精密机床Nanosys600对Al6061进行端面超精密车削实验，通过切削、面型轮廓测量、面型轮廓滤波、分析这一过程的循环迭代，并结合所述理论，辨识了由环境温度变化和x轴导轨直线度误差引起的面型误差。经调整后，降低了这2个系统误差所引起的干扰，使面型精度由轮廓滤波后的Pt1 510 nm提升至Pt203 nm。