基于MATLAB的行走机构设计与优化
任军辉 穆龙涛 权 超
(陕西工业职业技术学院,陕西 咸阳 712000)
0 引言
移动机器人是现代机器人的一个重要分支,行走机构是其能够实现移动的结构保障。在所有行走机构中,连杆机构因结构简单、低副能承受较大的载荷、具有丰富的运动轨迹,能很好地实现移动机器人行走步态的要求[1]。平面铰链四杆机构是最简单,也是应用最广泛的连杆机构,可将其看作一个Ⅱ级杆组连接到原动件和机架上。只要在平面四杆机构上施加一个原动机就可实现复杂的平面运动轨迹[2]。在实际应用中,对行走机构的要求不同,可在四杆机构的基础上增加杆组,从而设计出较为复杂的多连杆系统[3],图1为六杆机械腿结构示意图。

图1 六杆机械腿结构拆分
对连杆机构进行设计的方法有作图法和解析法[4]。作图法是按照一定的比例尺,用几何作图的方式来求解连杆机构的尺寸参数,该方法较为简单直观、高效,但求解精度不高,对较为复杂的连杆系统求解较为困难;解析法是通过建立机构运动要求和机构尺寸参数间的解析方程式,并根据已知条件来求解出连杆的尺寸参数,且求解精度高。随着计算机技术的发展,解析法的求解更加方便。MATLAB提供了强大的数学计算能力,将研究的平面机构放于笛卡尔坐标系中,利用坐标矢量关系来建立求解表达式,即可实现对连杆机构的精确求解与优化[5-7]。
1 行走机构方案
一种基于连杆机构的四足机器人行走机构如图2所示,左右两侧的行走结构完全一致,但在运动状态上存在180°的相位差,可实现交替配合。每一侧机构中,前肢和后肢结构都是相似的平面四杆机构,通过曲柄共用一个电机。因此,在对其进行分析时,选取一侧的前肢结构对其进行分析与优化,其机构运动简图如图3所示。
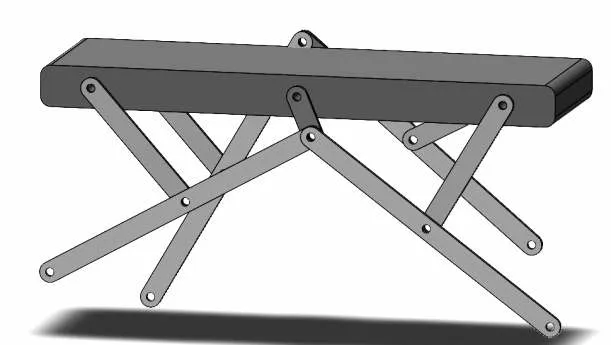
图2 四足行走机构
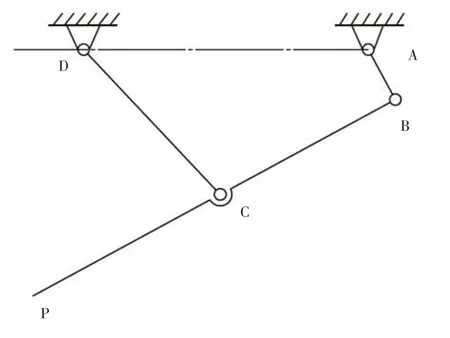
图3 机构运动简图
各杆件的尺寸为AB=200 mm、BC=700 mm、CD=700 mm、AD=1 000 mm。平面四杆机构曲柄存在的条件见式(1)。

式中:LAB为AB杆件的长度;LAD为AD杆件的长度;LBC为BC杆件的长度;LCD为CD杆件的长度。由图3可知,最短杆AB为曲柄,该四杆机构属曲柄摇杆机构。运动过程如下:AB杆件为原动件,电机通过减速装置来带动曲柄作整周转动,连杆为执行构件,P点为末端点,连杆上的某位置作高低起伏的复杂轨迹运动,从而实现与地面接触及抬起前进的行走动作。
2 机构运动和力分析
2.1 机构数学模型建立
为了能利用矢量来表示机构的几何关系,将四杆机构放置于平面直角坐标系中进行研究,如图4所示。四杆机构的四条边可构成一个封闭的图形,用矢量来表示每一段,即在封闭图形ABCD中,存在的矢量方程见式(2)。

式中:AB为杆AB对应的平面矢量;BC为杆BC对应的平面矢量;AD为杆AD对应的平面矢量;DC为杆DC对应的平面矢量。
为了便于求解导数,式(2)可用复数的形式来表示,见式(3)。

式中:|AB|、BC、|CD|、|AD|分别为AB杆、BC杆、CD杆和AD杆的长度;θ1,θ2,θ3分别为AB杆、BC杆、CD杆与水平方向的夹角(见图4)。

图4 行走机构的数学模型
其中,θ1随时间的变化规律就是曲柄的运动规律,待分析的变量包括其余杆件的角度,可利用MATLAB来求解式(3),以及角度相对时间求一阶导、二阶导,从而分析各杆件的位置、速度和加速度。
2.2 运动分析
在已知曲柄AB为主动件匀速转动的前提下,分析其余杆件的位置、速度和加速度的变化情况。由于平面四杆机构的自由度为1,在只有一个原动件的前提下,机构具有确定的运动。P点为连杆BC延长线上的一点,根据BC杆的运动规律可求出P点的运动情况。
对式(3)两侧同时求时间的一阶导数,见式(4)。

式中:ω1、ω2和ω3分别为AB杆、BC杆和CD杆的角速度。
为了便于MATLAB的编程求解,用矩阵的形式来表示速度方程,见式(5)。
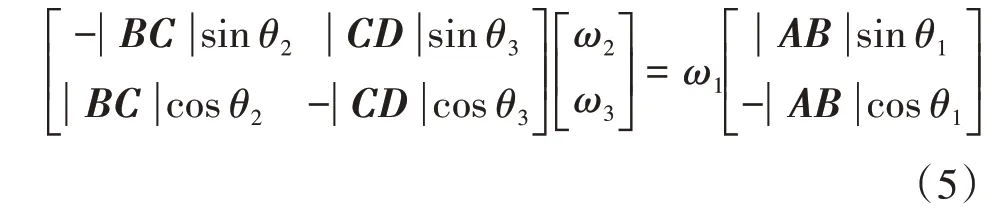
对式(3)两侧同时求时间的二阶导数,或对式(4)两侧同时求时间的一阶导数,得到加速度的方程式,见式(6)。

式中:α2、α3分别为杆BC、杆CD的角加速度。
根据计算结果,连杆和摇杆的运动规律如图5所示。
由图5可知,当曲柄转角分别为135°和330°时,CD杆的角速度达到最大值75 rad/s;当曲柄转角在27°和240°附近时,连杆BC达到最大角速度75 rad/s。在每一个运动周期中,连杆BC和摇杆CD的加速度波动范围分别为-2.2×104~1.4×104rad/s2、-1.5×104~2.2×104rad/s2。

图5 行走机构运动分析曲线
2.3 力分析
在运动分析的基础上,当杆件质量、质心位置、转动惯量以及执行件的工作阻力矩已知,可借助MATLAB软件来计算运动副上的受力,以及原动机所需的平衡力矩。对活动构件i进行受力分析,并根据受力分析来建立平衡方程,见式(7)。

式中:Si为质心;MSi为对质心Si的力矩;Fx为水平方向的作用力;Fy为垂直方向的作用力。
在行走机构中,对3个可移动的杆件可建立9个平衡方程,利用MATLAB进行求解,对工作阻力矩为100 N、杆件线密度为10 kg/m的案例进行分析,得到四杆机构C点转动副的受力和曲柄AB平衡力矩,如图6所示。
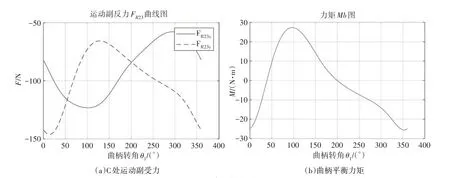
图6 行走机构力分析
3 行走机构优化设计
通过以上分析可以看出,连杆上的点的运动轨迹不尽相同,在图3中,行走机构末端执行点是连杆BC延长线上的一点,为了使行走机构具有良好的传力性能和越障能力,希望P点的运动轨迹能通过(1 200,-920)、(1 100,-900)、(900,-880)、(800,-910)、(700,-930)这5个点,以这5个点所在的曲线为理想曲线,根据数学模型可求解出轨迹上最接近理想曲线的连杆上某点位置,并将其作为P点的实际位置,从而实现对连杆机构的优化。目标函数见式(8)。

式中:(xPi,yPi)、(xi,yi)分别为理想曲线上的坐标点和P点轨迹上的坐标点。
由于P是实际构件上的一点,因此可以是BC线段外的点,但其与连杆是同一个构件。可用BP以及BP和BC之间的夹角θ来表示P点在实际连杆上的位置。优化的约束条件见式(9)。

式中:γ为传动角;γmin和γmax分别为传动角的最小值和最大值;|AB|、|BC|、|CD|、|AD|分别为AB杆、BC杆、CD杆和AD杆的长度。
由此来设计各杆长度以及P点在连杆上的位置。根据MATLAB的计算结果在三维建模软件中进行建模,如图7所示,即BP=633 mm、θ=13.4°。
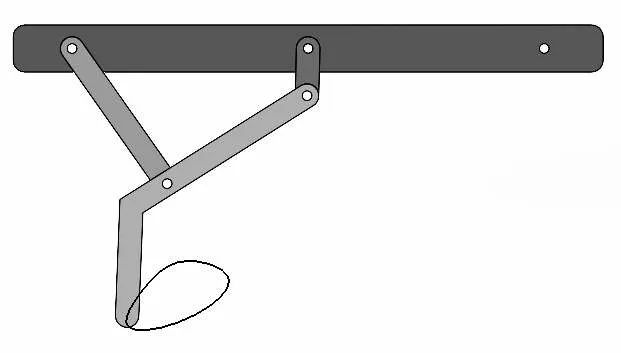
图7 优化后的结构即轨迹线
4 结语
本研究基于MATLAB的编程与强大计算能力,使用解析法对连杆行走机构进行运动和受力分析,并在此基础上,以末端轨迹为目标,对连杆进行优化,得出末端执行点的具体位置,使连杆行走机构具有良好的传力和越障性能,从而为精确分析和连杆机构设计提供参考。

