基于改进FCM算法的城市交叉口交通状态判别

刘宗锋， 杨凯利， 吴鲁香， 吴东平

(1.山东科技大学交通学院， 青岛 266590； 2.沈阳建筑大学交通工程学院， 沈阳 110168；3.山东华凌电缆有限公司， 济南 250220)

0 引言

目前，在智能交通系统研究领域中，交通运行状态的判别已经成为一个研究热点. 准确、实时的交通状态判别有助于交通管理部门及时了解和掌握城市整体的交通运行状况，同时也便于交通管理部门提前预估并制定城市交通拥堵的疏导决策方案，对缓解交通拥堵具有重要意义. 因此，国内外许多学者对交通状态判别的研究给予了高度的关注.

He等[1]选取速度性能指标作为路网状态评价指标，提出了1种用拥挤指数衡量拥堵程度的评价方法，并以北京市公路网为例进行了路段和路网拥堵评价. Bae等[2]选取密度数据，利用Gaussian 混合模型实现对高速公路交通状态的判别. 任其亮等[3]利用Relief F算法得到特征向量的权值，建立了基于改进的FCM算法(W-FCM)的综合判别模型，用于对城市交叉口交通状态的判别. Antoniou等[4]利用数据驱动的概念提出基于位置的目标路段状态判别的方法. 陈兆盟等[5]提出了1种以车头时距的方差和时间占有率为判别指标并结合交通信号控制优化的交通状态判别方法，结果表明，该方法可有效地判别过饱和交通状态. 商强等[6]提出1种谱聚类与随机子空间集成K最近邻的模型(SC-RS-KNN)，用于快速路交通状态的判别. 戴学臻等[7]利用集对分析与三角模糊数ɑ-截集耦合实现对城市道路交通状态的判别. 庄劲松等[8]建立1种模糊综合判别模型，实现对道路交通状态的判别. 蔡晓禹等[9]利用FCM算法实现对山地城市快速路交通状态的判别，并结合视频图像验证判别的准确度. 常丽君等[10]在FCM算法基础上进行优化，将概率神经网络(PNN)与基于遗传(GA)模拟退火(SA)的改进FCM算法相结合实现对交通状态的判别. 黄艳国等[11]利用马氏距离代替传统欧式距离实现对FCM算法的改进，使城市道路交通状态的判别结果更加准确.

由于交通状态很难用具体的数字来表示，具有不确定性和模糊性，模糊聚类算法被广泛应用在交通状态判别中，其中应用FCM算法来判别交通状态已经取得了不少成就，但是大多数的研究都是针对城市道路或者高速公路的，对城市交叉口交通状态判别的研究相对较少，其次，忽略了各特征参数之间的不均衡性，缺少对各判别指标权重的研究. 基于此，本文开展了对城市交叉口交通状态判别的研究，引入熵权法计算各判别指标的权重值，构建1种基于K-means算法和熵权法加权的改进FCM算法，实现对交叉口交通状态的快速判别，为交通管理者制定交叉口信号控制策略提供依据.

1 城市交叉口交通状态划分

1.1 判别指标的选取

用于描述城市交叉口交通状态的判别指标有很多，如到达率、平均延误时间、排队长度、平均运行速度、饱和度、车头时距等. 为了综合判别交叉口交通状态需要选取合理的判别指标，然而并不意味着选取的判别指标越多越好，而是要考虑选取的判别指标能对交叉口状态反应敏感且获取简单，因此，本文选取平均排队长度、平均延误、饱和度3个交通参数为判别指标，组成了交叉口交通状态判别指标体系.

1)饱和度

交叉口饱和度反映了整个交叉口交通负荷状况，其为各进口道饱和度的加权平均值[13]，并非各进口道饱和度之和：

(1)

式中，n为进口车道数；qi为进口道i的饱和度；Qi为进口道i的交通量(pcu/h).

2)平均延误

延误反映了交叉口交通状态，利用数学模型计算难度大，可通过仿真的形式比较容易获得.交叉口的平均延误：

(2)

式中，di为进口道i的平均延误(pcu/s)；其他符号同前.

3)平均排队长度

排队长度反映了交叉口的拥挤程度[14]，是指从停止线开始排队到排队末尾之间的距离.平均排队长度见式(3)：

(3)

式中，n为车道数；li为进口道i的平均排队长度(m).

1.2 交叉口交通状态划分

本文依据交叉口的交通流特性及拥堵强度，将城市交叉口交通状态分为畅通、缓行、拥堵3个状态，其对应的交通特征如下：

1)“畅通”状态：车辆较少，车辆行驶速度很高，不超过限速的条件下，驾驶员能自由地选择车速行驶，受到其他车辆的影响较小；

2)“缓行”状态：车辆不断增多，行驶速度降低，车辆行驶自由受限，延误增大；

3)“拥堵”状态：进口道的排队长度不断增加，导致车辆需要停车一次或者多次才能通过交叉口，行驶速度大幅降低.

2 交通状态判别方法

2.1 FCM算法

模糊C均值聚类算法是基于模糊理论的1种软分类算法，这种算法并不是把每个样本严格划为某1个类，而是通过迭代计算使非相似性指标的目标函数达到最小[15]，得到此时每个样本对于每个类的隶属度，用于确定每个样本的类属.

设特征空间中的数据样本集为X={x1，x2，x3，…，xn}∈RS，n代表样本的数量.FCM算法的目标函数是各个样本到各个类的欧式距离的和(误差的平方根)，用JFCM表示.

(4)

约束条件如下：

(5)

式中，m为模糊指数，当m∈[1.5,2.5]时，聚类效果最好[16]，故本文取m=2；uij为样本xj属于第i类的隶属度；c为聚类数目；dij为样本xj到聚类中心ci的欧氏距离.

2.2 熵权法

考虑到各判别指标在交叉口交通状态判别体系中所占的比例不同，通过对各指标设定不同权值来衡量对聚类结果的贡献大小，因此，引入熵权法对各指标的权重进行计算.熵权法是通过指标差异性大小确定权重，具有克服主观赋权方法主观性的优势，故计算各判别指标权重的步骤如下：

1)数据标准化处理.若有n组数据，m个判别指标，则构建数据矩阵X=[xij]n×m(i=1,2,…,n;j=1,2,…,m)并利用公式(6)标准化处理.

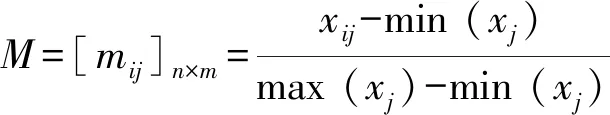
(6)

式中min (xj)、max (xj)分别为第j项判别指标的最小值、最大值.

2)计算第j项判别指标的熵值ej：

(7)

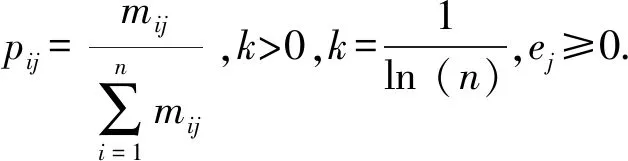
3)计算第j项判别指标的权重系数wj：

(8)

2.3 改进的FCM聚类算法

改进的FCM算法是将K-means算法、熵权法、FCM算法三者进行结合来实现对传统FCM算法的改进. 由于K-means算法具有收敛速度快的优势且得到的聚类中心与FCM算法得到的聚类中心较为相似，因此，利用K-means算法得到初始聚类中心，再利用熵权法计算各个指标的权重，得到基于判别指标加权的欧式距离度量方式，则加权的欧式距离表达式为

(9)

式中，ω=(ω1,ω2,…,ωt)，t为判别指标的个数，本文t=3，ωk∈[0,1]为判别指标的权值.

改进的FCM算法中的目标函数是利用上述的加权欧式距离来代替传统的欧式距离，用JEWFCM表示.

(10)

得到新的迭代解为：

(11)

(12)

改进的FCM算法进行交通状态判别的流程图见图1.

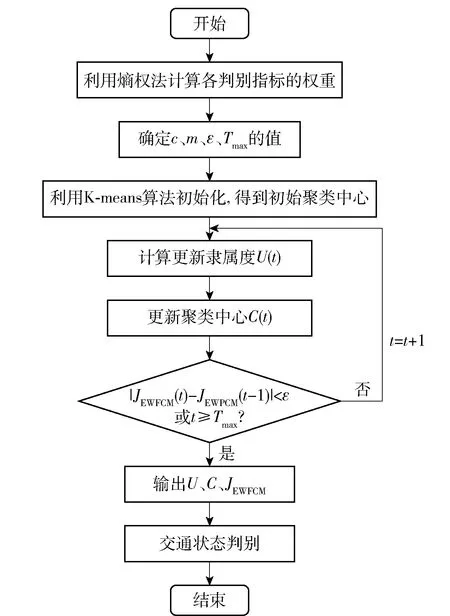
图1 改进FCM算法的交通判别流程图

2.4 算法评价指标

为了验证聚类算法的有效性，本文采用划分系数(PC)和划分熵系数(PE)2个指标对改进前后的FCM算法的聚类效果进行评价.

1)划分系数(PC)的值越大，说明算法的判别效果越好，PC可按下式计算：

(13)

2)划分熵系数(PE)的值越小，说明算法的判别效果越好，PE可按下式计算：

(14)

3 案例分析

3.1 交通数据采集

选取济南市某交叉口为研究对象，对该交叉口的交通状态进行判别应用. 据调查可知，该交叉口是信号控制交叉口，其配时方案见表1.

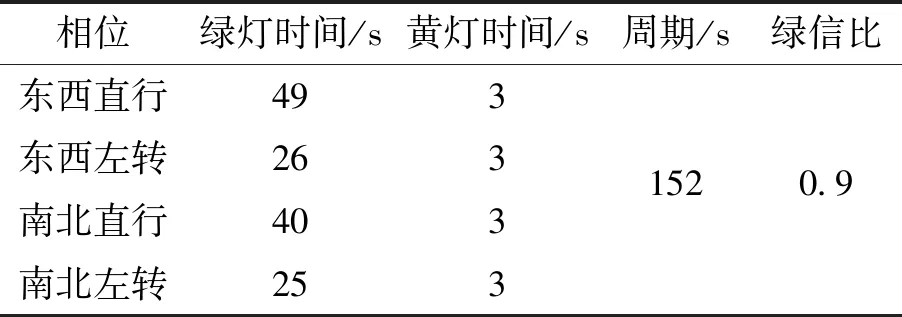
表1 信号配时方案

为了更全面地获取交叉口各个交通状态下的指标数据，本文利用实际获得交叉口的信号配时方案以及渠化信息，借助 VISSIM软件进行仿真模拟. VISSIM仿真软件获取指标数据简单，并且该软件能很好地表征交叉口的实际运行情况，因此，利用VISSIM仿真软件获取指标数据是可靠的，可将仿真数据用于对聚类算法的验证分析.

在仿真的过程中，通过对各进口道输入不同的流量数据来采集不同交通状态下各判别指标的数据，以5 min为时间间隔输出1组数据，共150组，通过对仿真数据整理计算得到每组数据包括交叉口交通状态划分的3个指标参数，依次为饱和度、平均延误、平均排队长度.

在仿真数据预处理的过程中需要依据熵权法计算交叉口各判别指标的权重，再利用改进前后的FCM算法得到交叉口交通状态的划分结果. 而数据的标准化处理是熵权法中的必要的步骤，其可提高FCM算法的准确性. 因此，在数据预处理时，首先将150组数据进行标准化处理，再利用熵权法计算出各判别指标的权重向量集，计算结果见表2.

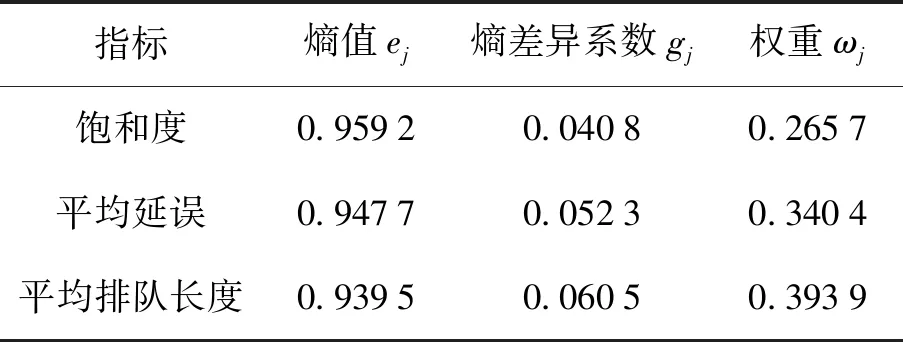
表2 基于熵权法的各判别指标权重值

由表2可知，交叉口交通状态的判别指标的权重向量集为ω=[ω1,ω2,ω3]=[0.265 7,0.340 4,0.393 9].

3.2 改进的FCM算法与FCM算法的聚类结果

改进前后的FCM算法进行聚类时，需要确定算法的参数：c=3，ε=1×10-3，m=2，Tmax=100.使用Python编程软件将交叉口150组的仿真数据分别通过2种聚类算法进行迭代计算，得到以下聚类结果：

1)FCM聚类算法聚类中心：

2)利用K-means算法得到初始聚类中心：

然后将权重向量集ω=[0.265 7,0.340 4，0.393 9]和初始聚类中心带入改进的FCM算法进行循环迭代计算，得到最终的聚类中心：

聚类中心矩阵的列表示各个判别指标在3种交通状态下的值，从左到右依次是饱和度、平均延误、平均排队长度；行表示每种交通状态下的3个指标值，从上到下依次是畅通、缓行、拥堵. 改进后的FCM算法采用是隶属度最大原则对交通状态进行划分，即每组数据对于每一类都会产生所对应的隶属度，其中哪一类的隶属度最大，则这组数据就属于哪一类，将样本的类别用不同颜色表示，红色、蓝色、绿色分别代表顺畅、缓行、拥堵3种状态，得到聚类结果空间分布见图2.

图2 改进的FCM算法聚类结果空间分布图

3.3 结果对比与分析

3.3.1 排队长度与迭代次数

对于聚类算法而言，目标函数值是用来衡量聚类中心能否准确的表示各分类中心，即目标函数越小，越能说明聚类中心能代表各分类中心，将改进前后的FCM算法进行多次运行，得到2种算法的样本目标函数值和迭代次数的结果见图3.

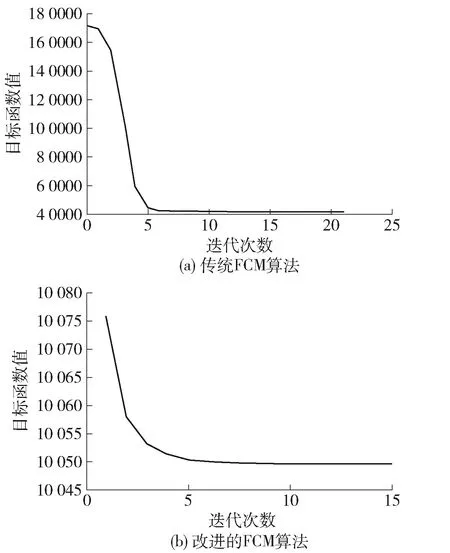
图3 改进前后FCM算法目标函数的对比

由图3可知，首次迭代时，改进的FCM算法的目标函数值约为10 076，FCM算法的目标函数值约为170 771，可得出改进的FCM算法的目标函数值远小于FCM算法的目标函数值，说明改进的FCM算法的初始搜寻目标优于FCM算法. 在迭代过程中，随着迭代次数的增加，2种聚类算法的目标函数值都呈现出逐渐下降的趋势. 当迭代结束时， FCM算法迭代了21次，目标函数值为41 849，而改进的FCM算法迭代了15次，目标函数值为10 049. 由上述可知，迭代次数由传统的FCM算法的21次降为15次，减少了28.6%，说明改进的FCM算法收敛速度更快；目标函数值由41 849降为10 049，降低了76.0%，且多次运行时改进的FCM的目标函数值趋于稳定，说明改进的FCM算法的稳定性更好. 综上所述，改进的FCM算法更适用于交叉口交通状态的判别.

3.3.2 算法有效性指标对比

利用PC和PE 2种有效性指标对改进前后的FCM算法进行评价，得到的计算结果见表3.

表3 改进前后FCM算法的有效性指标

从表3可知，对于PC和PE 2个评价指标，改进的FCM算法都比传统的FCM算法更优，说明改进的FCM算法聚类效果更好，更适用于处理大量的交通数据.

4 结束语

针对传统FCM算法判别交通状态时所存在的问题，本文提出将K-means算法、熵权法、FCM算法进行结合实现对传统的FCM算法的改进. 以获取简单且反应敏感的原则选取饱和度、平均延误、平均排队长度为判别指标，再利用改进前后的FCM算法对仿真数据进行聚类分析，以隶属度的大小作为交通状态判别的依据. 实例分析表明：本文所提的改进FCM算法相较传统的FCM算法，目标函数值降低了76.0%，迭代次数减少了28.6%，PC和PE 2个指标的评价结果更优，验证了改进的FCM算法的收敛速度更快、聚类性能更好，并且对城市道路交叉口交通状态划分的准确性更高. 此外，未来可在本研究的基础上开展对交叉口控制策略及信号配时优化的研究.