协变量在因果中介效应分析中的作用

胡纯严 ，胡良平 ，2*

（1.军事科学院研究生院，北京 100850；2.世界中医药学会联合会临床科研统计学专业委员会，北京 100029*通信作者：胡良平，E-mail：lphu927@163.com）

在传统的多重线性回归分析中，有3个隐含的前提条件，即假定全部自变量是同时存在的、地位平等的、互相独立的。而在许多实际问题中，某些自变量可能与另一些自变量之间并不独立，甚至存在显著的依赖关系［1］。因此，有必要将自变量划分成3种类型：处理变量（T）、中介变量（M）和协变量（C）。划分的依据、如何定义和识别变量之间的因果中介效应，是因果中介效应分析的基本内容。本文先介绍因果中介效应分析的理论基础，再结合一个实例，分别采用传统的多重线性回归分析［2］、不考虑协变量和考虑协变量的因果中介效应分析［3］，展示协变量在因果中介效应分析中的作用，并对分析结果进行比较和解释。

1 因果中介效应分析的概念和反事实框架

1.1 基本概念

在研究变量之间的依赖关系时，最简单的做法是将全部变量划分为自变量和因变量。这种划分是基于前述提及的3个隐含的前提条件，但在很多实际问题中，这些前提条件并不能满足。于是，统计学家将自变量划分为处理变量、中介变量和协变量［3］。处理变量：对结果变量Y有直接和间接因果效应的变量。在流行病学中，处理变量常被称为暴露与否。中介变量：处理变量T对其有直接因果效应，而它本身对结果变量Y又有直接因果效应。协变量：对处理变量T、中介变量M和结果变量Y都可能有影响的一组预处理或背景变量，它们混淆了观测到的Y、T和M之间的关系。

最简单的因果中介效应包括以下两种因果途径。直接途径：T→Y；中介途径：T→M→Y。第一个因果途径产生T对Y的直接效应，第二个因果途径产生T对Y的间接效应。假设Y、T和M都是连续变量，如果研究者忽略了因果关系，使用线性模型的形式构建Y关于T的回归模型，见式（1）。

式（1）中，e是一个误差项，其期望值为0，γ0是一个截距，则γ1被称为T对Y的总效应。该总效应是T对Y的总效应，而不涉及特定路径。一般来说，Y、T和M之间的关系由两个线性回归模型描述。见式（2）、式（3）。

式（2）和式（3）中，ε和δ是期望值为0的误差项，这两个回归模型的参数如下：β0是预测M的回归模型的截距，θ0是预测Y的回归模型的截距，β1是T→M路径的效应，θ1是T→Y路径的效应，θ2是M→Y路径的效应。将预测M的回归模型［式（2）］代入预测Y的回归模型［式（3）］中，得到式（4）。

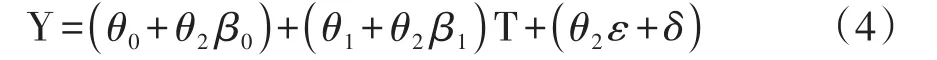
回归模型（4）是回归模型（1）的另一种表现形式，故它们等号右边的三项是对应相等的，于是，第二项的系数可写成如下关系式，见式（5）。

假设线性回归模型为真，则式（5）等号右侧的两个分量相加表示总效应。因为第一个分量θ1代表T→Y路径的直接效应，第二个分量θ2β1代表T对Y的非直接效应，或者只是T对Y的间接效应。研究者也可以直观地解释这个间接效应（θ2β1），它是沿着间接路径T→M→Y而产生的效应。因此，从概念上讲，总效应分解可写作式（6）。

直接和间接效应分量也由连续变量Y、T和M的线性回归模型中的参数定义。然而，总效应分解的说明在本质上是非常特别的，它基于对连续变量的线性回归模型进行比较，没有直接和间接效应的先验定义。因此，对于T和M之间存在相互作用效应的非线性模型或线性模型，式（6）将不成立。一个原因是分解中可能有2个以上的项，故直接-间接分解是不准确的；另一个原因是，在非线性模型中，各种效应会变得更加复杂，如何获得这些直接和间接效应分量尚不清楚。

通常情况下，协变量C会成为前述提及的三类变量Y、T和M的共同原因。在观察性研究中，Y、T和M之间的关联分为两部分：一部分是它们之间的实际因果关系；另一部分是C诱导的关联，这部分诱导的关联通常被称为混淆关联。为了在观察性研究中获得因果中介和相关效应的无偏估计，统计分析方法必须能够“消除”混淆关联。

1.2 定义因果中介效应的反事实框架

传统回归分析方法的一个问题是：缺乏一个提供因果中介和相关效应的明确定义的总体框架，故无法有效处理交互效应，无法在统一的框架内处理二值结果变量和二值中介变量。反事实框架为这个问题提供了解决方案［4-5］。在反事实框架内，直接和间接的效应都是根据反事实的结果来定义的。根据这些定义得出了分析结果，用于计算各种类型处理变量和结果变量的广泛参数模型下的因果中介效应［6］。有学者将这些结果扩展到了二值中介变量和计数结果变量，这一发展路线为因果过程提供了理论基础［7］。

反事实结果是研究者在假设干预下观察到的结果，即可能与事实结果相反的情景。以下符号用于表示干预措施的反事实结果：Yt是处理变量的水平被设置为T=t时，受试者的结果变量Y的反事实结果；Mt是处理变量的水平被设置为T=t时，受试者的中介变量M的反事实结果；Ytm是处理变量的水平被设置为T=t以及中介变量的水平被设置为M=m时，受试者的结果变量Y的反事实结果。这些符号对变量类型没有限制，变量Y、T和M可以是连续的，也可以是二值的。

假设处理变量是二值变量，t的取值是0或1，分别表示对照组和处理组。受试者的总效应（Total effect，TE）被定义为处理和对照水平的反事实结果的差异。见式（7）。

式（7）等号右边的2项中，Y的第一个下标表示处理变量的具体取值（为1或0）；第二个下标表示中介变量的具体取值（为M1或M0），M1为T=1条件下中介变量的取值，M0为T=0条件下中介变量的取值。

受试者的受控直接效应（controlled direct effect，CDE）被定义为两个处理水平的反事实结果的差异，即中介变量被设置为特定水平M=m时，见式（8）。

受试者的自然直接效应（natural direct effect，NDE）被定义为两个处理水平的反事实结果的差异，即中介变量的水平被设置为M=M0，这是没有中介变量参与时处理变量的自然水平，见式（9）。

受试者的自然间接效应（natural indirect effect，NIE）被定义为处理变量的水平被设置为T=1时，M1和M0两个中介水平的反事实结果的差异，见式（10）。

如果处理变量是连续的，那么必须根据感兴趣的处理和控制水平来定义处理变量的水平。例如，如果t1和t0是连续变量的处理和控制水平，并且，它们代表了实质性关注的水平，则它们应分别替换定义中处理和控制水平的1和0值。

以上给出的定义有两个重要属性：①它们导致总效应TE的以下常规双向分解，见式（11）；②它们独立于结果或中介模型。因此，它们和总效应分解适用于线性或非线性模型，无论T和M之间是否存在交互效应。

中介的总效应百分比（percentage of total effect that is mediated，PM）计算方法见式（12）。

VanderWeele［8］进一步介绍了总效应的以下四向分解，见式（13）。

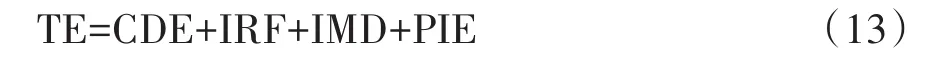
式（13）中，CDE为受控直接效应，IRF为参考相互作用，IMD为中介相互作用，PIE为纯间接效应，这4个组成部分的效应也被定义为反事实结果。

2 因果中介效应分析的实例与SAS实现

2.1 实例与数据结构

2.1.1 资料来源与背景信息

【例1】文献［3］提供的例子：仿照Marjoribanks讨论的理论教育模式［9］，模拟了一组数据，旨在了解父母提供的鼓励性环境（Encourage）是否会影响儿童的认知发展（CogPerform）。一个关键问题是，父母鼓励的效应是否部分归因于它增强了儿童的学习动机（Motivation）。父母鼓励效应可能通过以下两种途径来体现，直接途径：Encourage→CogPerform；中介途径：Encourage→Motivation→CogPerform。在中介分析的术语中，Encourage是处理变量或暴露变量，Motivation是中介变量，CogPerform是结果变量。假定已按照某种规则产生出300个观测数据的模拟样本，保存在名为Cognitive的数据集中，在此数据集中，每个观测有六个变量值，其名称和含义如下。CogPerform：儿童在认知测试中的得分；Encourage：问卷中关于父母鼓励行为的三个项目的总分；FamSize：儿童所在家庭的规模；Motivation：儿童、教师和主要监护人对儿童动机水平的评分；SocStatus：儿童的社会地位，是家庭收入、父母职业和父母受教育程度的综合衡量标准；StudentID：儿童的编号。其中，FamSize和SocStatus是背景或预处理变量（简称协变量），研究者希望在观测各种因果效应时对其进行控制。试基于以上资料，分析处理变量、中介变量和协变量对结果变量的因果中介效应。

2.1.2 创建用于因果中介效应分析的数据集

设所需要的SAS程序如下：

【说明】详细数据见文献［3］，此处从略。

2.2 使用SAS实现因果中介效应分析

2.2.1 基于传统的多重线性回归分析方法计算

【分析与解答】设所需要的SAS程序如下：

【SAS程序说明】model语句的等号后列出了4个变量，即把协变量（FamSize和SocStatus）、处理变量（Encourage）和中介变量（Motivation）视为地位平等的自变量。

【SAS主要输出结果及解释】因篇幅所限，输出结果从略。现将主要内容解释如下：两个协变量（FamSize和 SocStatus）对结果变量（CogPerform）的影响无统计学意义，将它们删除后重新建模，主要输出结果见表1。

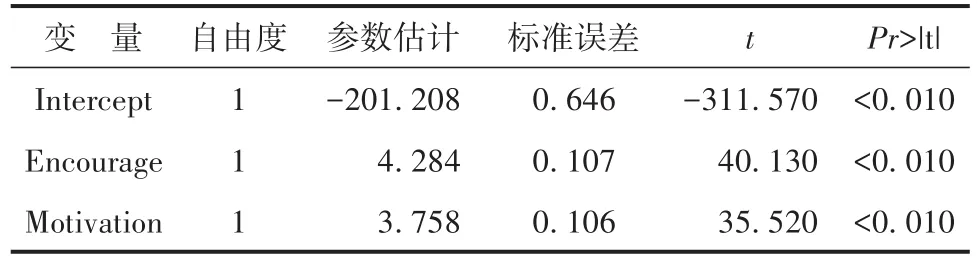
表1 精简后的传统多重线性回归分析结果Table 1 Simplified traditional multiple linear regression analysis results

与模型中保留2个协变量所得到的结果（此处未输出）相比，由表1可看出：处理变量（Encourage）和中介变量（Motivation）对结果变量（CogPerform）的影响略有提升，说明被删除的两个协变量对处理变量（Encourage）和中介变量（Motivation）的混淆作用似乎不严重。

2.2.2 因果中介效应回归分析的计算

2.2.2.1 不考虑协变量的影响

【分析与解答】以下语句调用proc causalmed来估计各种效应，而不控制协变量。设所需要的SAS程序如下：

【SAS程序说明】proc causalmed语句中的all选项显示所有可用输出。model语句指定了CogPerform的结果模型，该模型受Encourage和Motivation变量的影响。mediator语句指定了Motivation的中介模型，该模型仅受Encourage变量的影响。

【SAS主要输出结果及解释】总共有三部分输出结果。第一部分主要输出结果见表2。所有效应估计和百分比估计都具有统计学意义。总效应估计值为8.042，分解为自然直接效应（NDE=4.284）和自然间接效应（NIE=3.759）。估计的受控直接效应（CDE）为4.284，在默认情况下，以中介变量动机的平均值进行评估。在当前模型中，CDE与NDE相同。中介变量所占百分比为46.738%。表明在父母鼓励对儿童认知发展的效应中，只有不到一半可归因于儿童学习动机的增强。

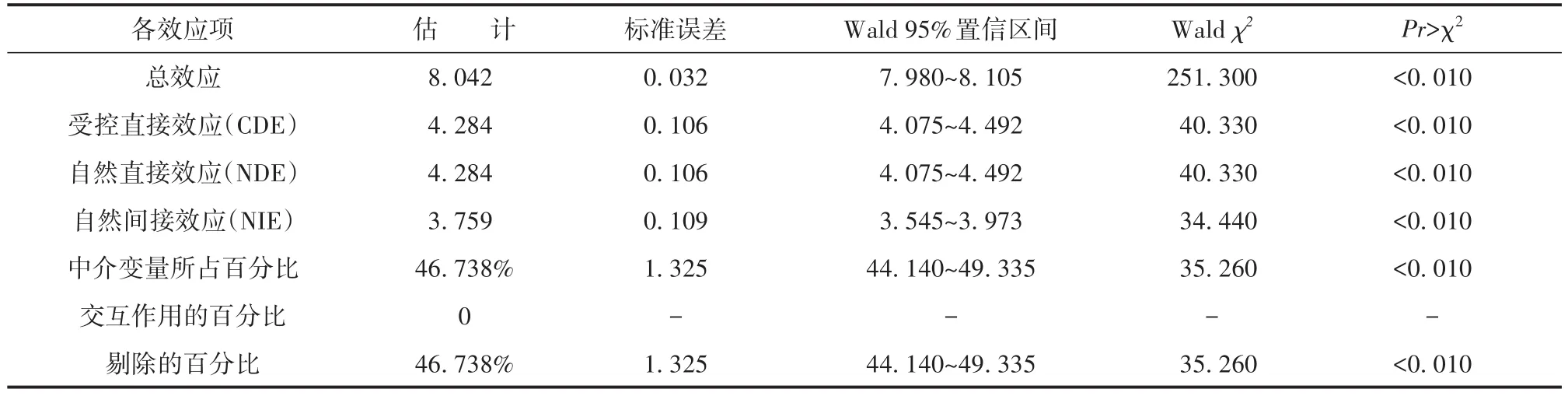
表2 计算所得的总效应、直接效应和中介效应的汇总Table 2 Summary of calculated total，direct and mediated effects

第二部分主要输出结果见表3。结果变量（CogPerform）模型的参数估计和假设检验的结果，截距项和两个回归系数与0之间差异均有统计学意义。说明处理变量和中介变量对结果变量（CogPerform）的正向影响是不可忽视的。

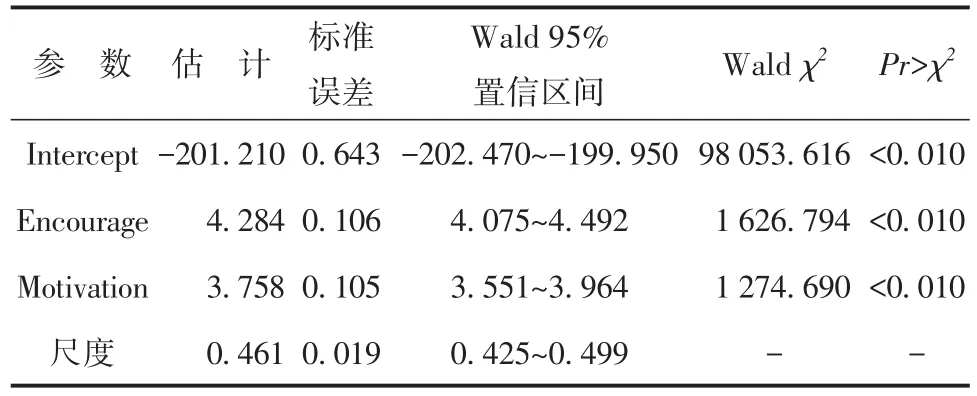
表3 含处理变量和中介变量的模型中参数的估计结果Table 3 Estimation results of parameters in the model with treatment variable and mediated variable

第三部分主要输出结果见表4。由结果可知：父母的鼓励（Encourage）对中介变量（Motivation）的积极影响是不可忽视的。

2.2.2.2 考虑协变量的影响

虽然前面的分析结果是可以解释的，但它没有充分利用因果中介效应分析过程中可用的因果分析技术。为了从观测数据中得出有效的因果解释，研究者必须对所有重要的混杂背景变量（即协变量）进行统计控制。假设FamSize和SocStatus是需要控制的混杂变量，设所需要的SAS过程步程序如下：

主要输出结果见表5。由表5可知，处理变量对结果变量的总效应为6.844，比分析中不包括混杂协变量的总效应8.042（表2中的第二行第二列）低了约1.200。这种差异表明，所观测到的处理变量和结果变量之间的关联，部分是由它们和协变量之间的关联所致。未对协变量进行调整，导致表2中对总因果效应的估计过高。当前分析中的NDE为4.296，与之前的分析结果接近。然而，NIE为2.547，比表2中的NIE低1.212。此外，中介变量所占百分比为37.222%，比表2中的中介变量所占百分比（46.738%）低9.516%。

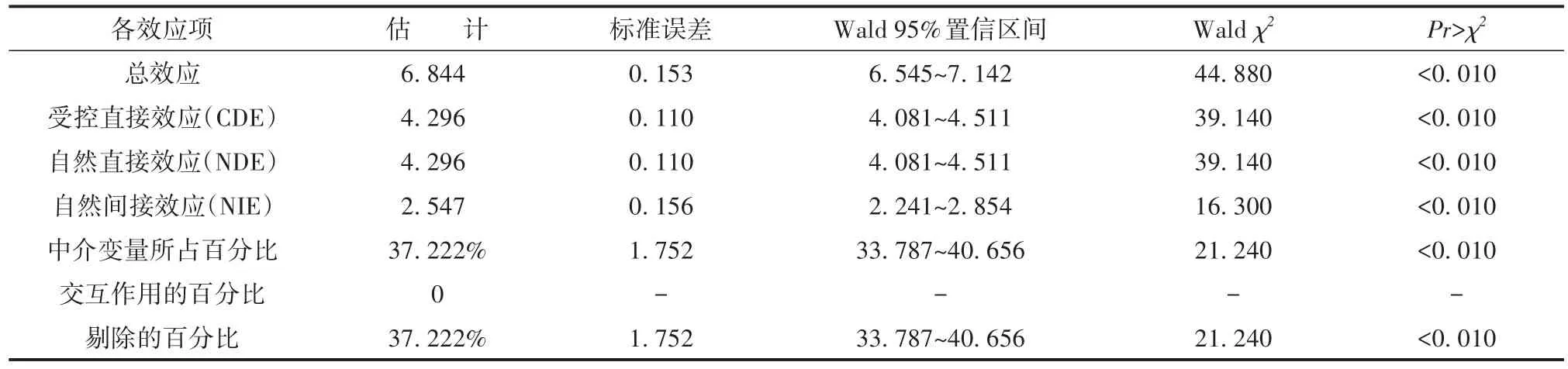
表5 考虑协变量的总效应、直接效应和中介效应汇总Table 5 Summary of total，direct and mediated effects considering covariates

因此，进行因果中介效应分析应考虑以下3点：①当资料中包含中介变量时，不适合采取传统的多重线性回归分析；②当资料中包含协变量时，不应在忽视协变量的情况下进行因果中介效应分析；③观测数据的因果分析可能涉及许多其他需要关注的假设，因篇幅所限，此处从略。

3 讨论与小结

3.1 讨论

在对本文例1的分析中，有一个隐含的假设，即处理变量和中介变量与结果变量之间没有交互作用。事实上，该假设不一定成立。Proc causalmed过程支持具有交互作用的结果模型；在许多实际问题中，数据必须满足时间条件，以便观测处理变量对结果变量的效应、处理变量对中介变量的效应以及中介变量对结果变量的效应。有时，多重线性回归分析显示，协变量对结果变量的影响无统计学意义，而因果中介效应分析则显示协变量的作用不可忽视。

3.2 小结

本文介绍了因果中介效应分析的理论基础，通过一个实例演示了如何使用SAS实现因果中介效应分析。理论基础主要包括基本概念和定义因果中介效应的反事实框架两个部分；通过采用多种方法分析例1，其结果提示应注意以下两点：其一，当资料中存在中介变量时，不适合采用传统的多重线性回归模型进行分析；其二，在因果中介效应分析中，不应忽视协变量的作用。