基于“对称性”思维考查关键能力的试题赏析及教学启示——以2022 年全国高考甲卷理综物理第21 题为例

罗培雄 陈建新

（1.晋江市南侨中学，福建 晋江 362200；2.晋江市教师进修学校，福建 晋江 362200）

从科学思维的角度来说，“对称性”思维的最有效功能是培养学生的直觉思维能力、分析能力和推理能力。考生需要对物理现象的深入分析，抓住事物的本质，总结归纳物理的规律。现以2022 年全国高考甲卷理综物理第21 题为例，赏析这类物理试题模型的对称性特征，探讨从考查关键能力方面带来的教学启示。

一、试题分析

（一）原题再现

例1.（2022 年全国高考甲卷理综第21 题）地面上方某区域存在方向水平向右的匀强电场，将一带正电荷的小球自电场中Р 点水平向左射出。小球所受的重力和电场力的大小相等，重力势能和电势能的零点均取在Р 点。则射出后，（ ）。

A.小球的动能最小时，其电势能最大

B.小球的动能等于初始动能时，其电势能最大

C.小球速度的水平分量和竖直分量大小相等时，其动能最大

D.从射出时刻到小球速度的水平分量为零时，重力做的功等于小球电势能的增加量

（二）关键能力分析和物理模型对称性赏析

物理学科的关键能力包含理解能力、推理论证能力、模型建构能力、实验探究能力和创新能力等五种能力。［1］本题没有直接给出实际的物理模型，需要考生根据文字的表述构建出物理模型。如图1 所示，本题考查了学生模型建构能力。考生再根据对小球的运动分析，应用所学的物理规律解题，展示推理分析能力。本试题是一个很有内涵的“学习探索问题情境”，也是学生熟悉的典型问题情境，命题者通过设问的改变，将典型模型推陈出新，很好地考查学生的科学思维能力。

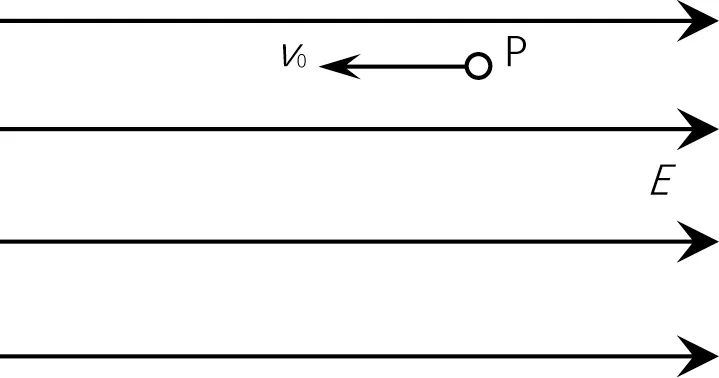
图1

粗看试题似乎与对称性没有直接的关系，但仔细分析小球的运动轨迹，便可以发现其中的奥秘。由于Eq=mg，故等效重力G＇的方向与水平成45°，则小球的运动可以看成类斜抛运动，如图2 所示。从对称性思维角度来分析，斜抛运动可以分解为两个平抛运动的关于线性对称，再利用运动学规律，即可迎刃而解。

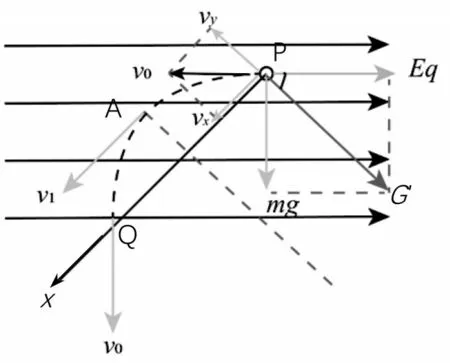
图2

（三）试题解析

如图2 所示，当vy=0 时速度最小，小球运动到轨迹的等效最高点A，此时的速度方向与水平方向成45°，小球速度的水平分速度和竖直分速度大小相等，此时小球的动能最小；而根据斜抛轨迹的对称性可知Q点为小球离P点沿电场线最远的点，也是小球运动轨迹电势最高的点，故小球在Q点的电势能最大；同时当小球运动到Q点时，等效重力G′不做功，此时的动能与初始动能相同。根据斜抛对称性，小球运动到Q点时，其速度方向与x 轴夹角也为45°，即此时的速度竖直向下，速度的水平分量为零，动能与初始动能相同，根据能量守恒定律可知，小球重力势能的减少量等于小球电势能的增加量，即重力做的功等于小球电势能的增加量。故选BD。

二、对称性思维拓展应用

（一）用对称性思维巧解等量电荷的电场问题

如图3 和图4 分别为等量同种电荷和等量异种电荷的电场分布图，电场强度关于两电荷连线、中垂线和中心O点对称，在对称点上场强大小均相等，关于两电荷连线对称点上的电势均相等，具有很好的对称性，利用电场分布的对称性特征，可以快速解题。

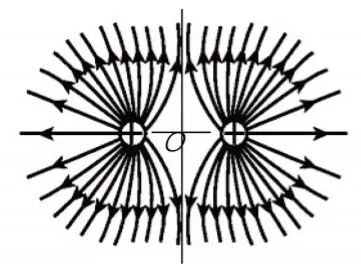
图3

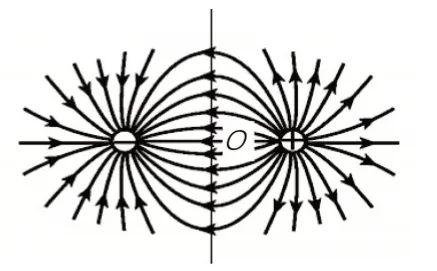
图4

例2.（2021 年福建省高考第15 题）如图（a），同一竖直平面内A、B、M、N四点距O点的距离均为，O为水平连线AB的中点，M、N在AB连线的中垂线上。A、B两点分别固定有一点电荷，电荷量均为Q（Q>0）。以O为原点，竖直向下为正方向建立x 轴。若取无穷远处为电势零点，则ON上的电势φ随位置x 的变化关系如图（b）所示。一电荷量为Q（Q>0）的小球S1以一定初动能从M点竖直下落，一段时间后经过N 点，其在ON段运动的加速度大小a随位置x的变化关系如图（c）所示。图中g为重力加速度大小，k为静电力常量。

（1）求小球S1在M点所受电场力大小。

（2）当小球S1运动到N点时，恰与一沿x轴负方向运动的不带电绝缘小球S2发生弹性碰撞。已知S1与S2的质量相等，碰撞前、后S1的动能均为，碰撞时间极短。求碰撞前S2的动量大小。

（3）现将S2固定在N点，为保证S1能运动到N点与之相碰，S1从M点下落时的初动能须满足什么条件？

1.关键能力分析和模型对称性赏析

本题结合电势分布φ-x图象和运动a-x图象，考查考生从图象中获取信息的能力，对物理模型进行推理分析，提升解决实际问题的能力，符合高考评价体系中的思维认知能力群考查要求。

本题设计时只画出沿x 轴正方向的电势分布图象，利用等量同种电荷的对称性可以画出在x 轴上各点的电势分布图象，如图5 所示，又φ-x图象的斜率反映场强的大小，如此我们就可以清楚地分析小球从M点到O点的运动情况，特别对第（3）的解决能起到事半功倍的效果。

图5

2.用对称性思维详解第（3）问

设O点上方处为D点。根据图（c）和对称性可知，S1在D点所受的电场力大小等于小球的重力大小，方向竖直向上，S1在此处加速度为0；S1在D点上方做减速运动，在D点下方做加速运动，为保证S1能运动到N点与S2相碰，S1运动到D点时的速度必须大于零。

设M点与D点电势差为UMD，由电势差定义有

设小球S1初动能为EK，运动到D点的动能为EKD，由动能定理有

由对称性，D点与C点电势相等，M点与N点电势相等，依据图（b）所给数据，并联立①②③④式可得：

（二）用对称性思维巧解碰撞类问题

1.碰撞模型分析

两物体发生弹性碰撞或类弹性碰撞时，计算碰后的速度涉及二元二次方程组的求解，计算难度比较大。但通过计算我们会发现，两物体碰前的速度大小和碰后速度大小与系统的质心速度（即共同速度）存在一定的关系，现以如图6 的模型为例来分析。设A球的质量为m1，B球的质量为m2，A球与B球发生弹性碰撞。根据动量守恒定律和能量守恒定律有

图6

联立以上两式可得

两球在碰撞过程中某时刻会速度相等，设为v共，根据动量守恒定律有

2.对称性思维在碰撞问题中的应用实例

例3.（2020 年高考全国丙卷理综物理）甲、乙两个物块在光滑水平桌面上沿同一直线运动，甲追上乙，并与乙发生碰撞，碰撞前后甲、乙的速度随时间的变化如图8 中实线所示。已知甲的质量为1kg，则碰撞过程两物块损失的机械能为（ ）

图8

A.3 J B.4 J C.5 J D.6 J

图7

分析：由图象可知v甲和v甲′没有关于v共对称，或v甲-v乙>v乙′-v甲′，因此甲、乙两个物块的碰撞一定为一般非弹性碰撞，碰撞过程有机械能损失。

例4.（2022 年高考全国乙卷理综物理）如图（a），一质量为m的物块A与轻质弹簧连接，静止在光滑水平面上：物块B向A运动，时与弹簧接触，到时与弹簧分离，第一次碰撞结束，A、B的v-t图像如图（b）所示。已知从t=0 到t=t0时间内，物块A运动的距离为0.36v0t0。A、B分离后，A滑上粗糙斜面，然后滑下，与一直在水平面上运动的B再次碰撞，之后A再次滑上斜面，达到的最高点与前一次相同。斜面倾角为θ（sinθ=0.6），与水平面光滑连接。碰撞过程中弹簧始终处于弹性限度内。求：

（1）第一次碰撞过程中，弹簧弹性势能的最大值；

（2）第一次碰撞过程中，弹簧压缩量的最大值；

（3）物块A与斜面间的动摩擦因数。

分析：物块A和B及弹簧构成的系统，碰撞过程为弹性碰撞，它们碰撞前后的速度必然满足与v 共对称，碰撞过程的时间也满足t2=2t1，其中t2为碰撞过程的总时间，t1为开始碰撞到共速的时间。

由图（b）数据得以验证。本题设计的问题涉及变力做功和变力冲量问题，需要用到能量和动量的原理求解，在此不做展开，类似的弹簧碰撞碰撞问题还有很多经典题型。

三、教学启示

（一）明确高考评价体系改革的方向，提升学生关键能力

高考评价体系为物理考试内容的改革指明了方向，［1］高考试题将更注重对学生关键能力的考查。试题的应用性和综合性都在提升，考查学生的推理能力和应用数学解决物理问题等关键能力，同时增加试题的灵活性，引导学生减少机械刷题的低效学习方式。教师在教学过程中应该注重培养学生的分析、推理、模型构建及数学知识的应用能力，提升学生的关键能力，促进学生的物理学科核心素养的形成。

（二）重视物理规律的分析，培养学生的科学思维

物理规律是反映物理现象、物理过程在一定条件下必然发生、发展和变化的规律，［2］掌握物理规律就可以用它去认识、分析、解决物理世界的各种问题。如抛体运动的对称性规律，理想气体的状态变化规律，电流变化的欧姆定律，世界万物间引力定律，电荷间相互作用的库仑定律等等，可以解决运动、气体、力学、电学等一系列问题。近几年的高考试题情境推陈出新，并将基本概念和基本规律融入试题情境中，让学生感到熟悉而又陌生，充分考查学生挖掘图象信息和如何巧用物理规律解题的科学思维能力。教师在教学过程应注重学生科学思维的培养，可以通过物理规律的分析，问题对比分析，一题多解等发散思维的训练，达到提升学生的科学思维能力。