与Qα,β算子相关的多叶函数从属关系的研究①

夏年红

(安徽卫生健康职业学院基础部,安徽 池州 247099)

1 引 言

定义1.设Ap表示在单位圆盘U={z∈:|z|<1}内解析，具有形式

的p叶解析函数类.

定义2.设f(z)和g(z)在单位圆盘U内解析，如果存在一个解析函数w(z),w(0)=0且|w(z)|<1(z∈U)，满足f(z)=g(w(z))，则称f(z)从属于g(z)，记为f(z)g(z)(z∈U).

特别地，如果g(z)在U内单叶，那么f(z)g(z)当且仅当f(0)=g(0)且f(U)⊂g(U).

定义3.设H(p(z),zp′(z))h(z)为一个一阶微分从属，q(z)为单叶函数，若对所有满足此微分从属的解析函数p(z)，都有p(z)q(z)，则称q(z)为此微分从属的一个控制.若是微分从属的一个控制函数，且对所有控制q(z)都满足则称为最佳控制.

定义4.若函数f(z)∈Ap满足条件：

则称f(z)为p叶星象函数.

定义5.定义积分算子Qα,β如下

Qα,βf(z)=

(α≥0,β>-1)

(1)

其中Γ表示Gamma函数，

在等式(1)两边求关于z的q次微分，得到下面的微分算子：

这里

以上知识是为研究与Qα,β积分算子有关的多叶函数的高阶导数从属关系做铺垫.

2 相关引理

为了更详细的分析所要研究的问题，需要借助以下引理.

引理1[2]设R(z)是U中单叶函数，φ(z)是域D中的解析函数，R(U)⊂D，如果zR′(z)·φ[R(z)]是星象的，p(z)是U中解析函数，且p(0)=R(0),p(U)⊂D，那么

zp′(z)·φ[p(z)]zR′(z)·φ[R(z)]⟹p(z)R(z)

且R(z)是最佳控制.

引理2[2]设R(z)是U中凸单叶函数，θ(z)是域D中的解析函数，R(U)⊂D.假设

如果p(z)是U中的解析函数，且p(0)=R(0),p(U)⊂D，那么

zp′(z)+θ[p(z)]zR′(z)+θ[R(z)]⟹p(z)R(z)

且R(z)是最佳控制.

3 主要结果与证明

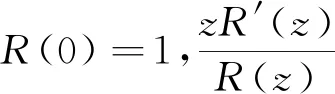
(2)

那么

且R(z)是最佳控制.

证明：设函数

(3)

则p(z)在U内解析，p(0)=1. 对(3)进行对数微分，得到：

因此

(4)

从而

(5)

结合(2)式，可得：

或者

zp′(z)·φ[p(z)]zR′(z)·φ[R(z)].

由于R(z)≠0，φ(ω)是包含R(U)域内的解析函数，并且

是星象的，由引理1可知p(z)R(z)，即

且R(z)是最佳控制，定理得证.

定理2设R(z)是U中凸单叶函数且R(0)=1，如果f(z)∈Ap满足

(6)

那么

且R(z)是最佳控制.

证明：设函数

由(4)式得：

结合(6)式得：

zp′(z)zR′(z),

也可以表示成

zp′(z)·φ[p(z)]zR′(z)·φ[R(z)].

这里φ(ω)=1.由于R(z)是凸函数，从而zR′(z)·φ[R(z)]=zR′(z)是星象的，由引理1可知p(z)R(z)，即

且R(z)是最佳控制.定理得证.

定理3设R(z)是U中凸单叶函数且R(0)=1.如果f(z)∈Ap满足

(7)

那么

且R(z)是最佳控制.

证明：设函数

由(5)式得：

结合(7)式得：

zp′(z)+(p-q)p(z)zR′(z)+(p-q)R(z)

也可表示成

zp′(z)+θ[p(z)]zR′(z)+θ[R(z)],

这里θ(ω)=(p-q)ω.引理2的条件显然都满足，因此p(z)R(z)，即

且R(z)是最佳控制.定理得证.

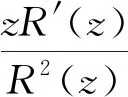
(8)

那么

且R(z)是最佳控制.

证明：设函数

由(4)式知：

结合(8)式得：

也可以表示成

zp′(z)·φ[p(z)]zR′(z)·φ[R(z)].

且R(z)是最佳控制.定理得证.