单元教学模式下“点到直线的距离”的新课教学探究

南通市小海中学 张中华

本节课是普通高中教科书苏教版选择性必修一第一章第五节第二课时，它是平面解析几何“直线”这一章内容的最后一节.主要内容就是点到直线的距离公式推导及应用.为了让学生将本章知识熟悉地带到这节新课的公式推导中，笔者采用了单元教学的模式来设计本节课.以下是本节课的教学过程及设计思路.

活动一：实例引入.

如图1，某渔排M的施工船P正在海中进行施工作业，接到台风预警通知：某台风在海洋中成型，其中心为T，已知台风的影响范围是半径为r的圆形，运行轨迹为与渔排一边平行的直线.请同学们结合图2用数学的眼光观察世界，来说说由此实例，能提出哪些问题？

图1

图2

用数学的眼光观察世界用数学的眼光观察世界(1)开始时,船P是否有危险?(1)求点P与点T之间距离,与r比较(2)台风运行过程中,船P是否有危险?(2)求点P到直线的距离,与r比较(3)台风运行过程中,渔排是否有危险?(3)求渔排M靠近台风的一边到直线的距离,与r比较

设计思路：用了常见的实际问题引入，但又用了不常规的开放性式提问，让学生用数学的眼光来审视这个世界，充分调动他们的积极性，让他们发散性地去思索这个实例能带来的问题，并且用数学的思维来思考解决所提出的问题.让他们体会实际问题数学化的转化过程以及用数学的思维来反馈解决实际问题的能力.

活动二：提炼思维，引出课题(如图3).

图3

设计思路：对前面学生所提出的三个数学问题，运用单元教学模式的思想，提炼成三个距离问题.(1)两点之间距离(已学知识)；(2)点到直线距离(本课所学)；(3)直线到直线之间的距离(本课知识扩充).再借助两点之间距离公式的推导方法进而衍生点到直线距离的推导方法，进一步转化出两平行直线之间的距离公式的推导方法.

活动三：深入探究，推导公式(如图4).

图4

组织学生分组讨论，把推导点到直线距离公式的三种方法具体化，让学生对具体的思维明朗化.接下去，学生分组推导公式并上台展示.

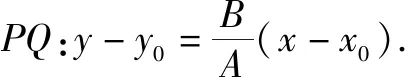
即

两式分别平方并相加，得

(A2+B2)[(x1-x0)2+(y1-y0)2]=(Ax0+By0+C)2.

通过整体思想，能简化运算.

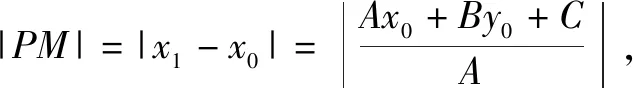
又PQ是Rt△PMN斜边上高，则

生丁：法三.设点T(x,y)，则PT2=(x-x0)2+(y-y0)2，消去y化简，得

生戊：以上的解答都要对A=0及B=0加以检验.

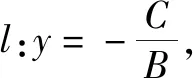
设计思路：以学生小组讨论的方式，并用流程图的形式把三种方法的思维明朗化.在此过程中，充分调动学生的积极性，并且使他们对三种方法的理解更加彻底.之后让学生分组合作推导公式以加深学生对方法的理解及提升处理多参数的运算能力.在运算的过程中，学生主动发现法一可通过整体思想来简化运算，可以此加深学生对整体思想的运用，这样为以后直线与圆及直线与圆锥曲线中的整体计算打下铺垫.最后，由学生来指出推导过程要缜密并对特殊情况加以验证.这样，既增强了学生的逻辑思维能力和合作能力，又加深了数学思维的缜密性，一举多得.

活动四：运用公式，加深理解.

引导学生推导两条平行直线Ax+By+C1=0，Ax+By+C2=0(C1≠C2)之间的距离公式.

生：两条平行直线间的距离，在一条直线上取点，即可转化为点到直线的距离.

过程如下：在Ax+By+C1=0上取点P(x0,y0)，则点P(x0,y0)到直线Ax+By+C2=0的距离

又Ax0+By0+C1=0，即Ax0+By0=-C1，则

师：至此，回到板书，就可补充完整了.

例1分别求点P(-1,2)到下列直线的距离：

(1)y=-2x+10；(2)3y+5=0；(3)3x=2.

例2求两条平行直线x+3y-4=0与2x+6y-9=0之间的距离.

例3已知直线l过原点，且点M(5,0)到直线l的距离为3，求直线l的方程.

设计思路：通过推导两条平行直线间的距离公式加深学生对形的认识以及形转化为数的能力，并且加深对点到直线距离公式的理解.通过例1加深学生对公式的运用并且对直线垂直于x轴或平行于x轴这两种特殊情况的认识，即可直观地从形解决，亦可应用公式.通过例2，引导学生注意两条平行直线间距离公式的细节，即直线一般式方程中x，y前的系数应相等.通过例3，加强学生对公式真正在具体问题中的应用能力.

本节课的板书设计即为活动二中的图3.本文中的课堂设计，在立意上没有单纯地从点到直线的距离这一知识点出发，而是通过单元教学模式，由具体的实例，把这一章节中的三个距离统一地提炼出来，让学生自主发现问题、提出问题、解决问题.这样，加深学生对这三个距离之间关系的认识，更加透彻地理解知识的本质.